伴随时间的模糊聚类协同过滤推荐算法*

阎红灿，王子茹，李伟芳，谷建涛

(1.华北理工大学理学院，河北 唐山 063210;2.河北省数据科学与应用重点实验室,河北 唐山 063000)

1 引言

随着推荐技术在电子商务、社交网络等互联网领域的广泛应用，面对海量的数据信息，如何除去冗余数据，为用户(消费者)推荐最需要或合适的服务产品(商品)成为研究热点。消费者试图通过每天接触的网页浏览来选购符合自己要求的商品，如何又准又快地为消费者推荐更心仪的商品，这就使推荐算法的准确性成为关键性问题[1 - 3]。

Goldberg等[4]首次提出推荐系统，找出用户评分数据中和目标用户有相同偏好和取向特征的用户，将这些用户感兴趣的商品推荐给目标用户[5]，但存在运行效率不高的问题。许多研究者提出填充稀疏数据集[6]、矩阵分解[7]和聚类[8]等方法，汪军等[9]提出了基于云模型熟悉相似度的邻居用户选择方法;袁泉等[10]提出用知识图谱进行推荐；Wu等[11]证明基于聚类的协同过滤可以明显提高推荐的准确性；王卫红等[12]用聚类和Weighted Slope One算法填充未评分项，提高推荐准确性；李娴等[13]用异质信息网络方法进行稀疏值填充；邢长征等[14]提出填充法和改进相似度相结合的协同过滤算法；文献[15]采用构建矩阵变换的形式增强了推荐的准确性和多样性；苏庆等[16]引入改进模糊划分的GIFP-FCM算法，将属性特征相似的项目聚成一类，构造索引矩阵，寻找最近邻居构成推荐；邓秀勤等[17]将用户喜好问题加入推荐的过程中，降低计算复杂度；张艳红等[18]提出对用户的坐标象限模糊隶属结果，提高推荐准确性。虽然加权斜率可以缓解稀疏性，没有考虑项目之间的隐含信息，加入模糊聚类可以提高推荐准确性，但有时人们的兴趣会随时间的迁移发生变化，如何更好地缓解以上问题成为优化算法的关键。

本文针对以上问题深入研究，提出伴随时间因子的模糊聚类协同过滤推荐算法，首先建立用户-项目评分矩阵，采用SMOTE(Synthetic Minority Oversampling TEchnique)过采样技术填充未评分项和时间，引入模糊聚类确定相同兴趣用户集合，在降低计算复杂度的前提下提高推荐准确性；同时引入时间因子改进传统评分过程，提高计算效率的同时保证了推荐算法的实时性。

2 相关理论

2.1 协同过滤推荐算法

协同过滤推荐算法通过用户与产品之间的关系，利用已有选择历史或用户间的相似关系，搜索用户潜在的感兴趣的项目，完成推荐。主要包括基于模型的协同过滤推荐算法和基于记忆的协同过滤推荐算法，而基于记忆的协同过滤算法又可以分为基于物品的协同过滤推荐算法和基于用户的协同过滤推荐算法，但是目前传统的协同过滤推荐算法大部分是基于矩阵运算，维度高、复杂性大，导致推荐准确度低，推荐效果较差。本文主要研究基于用户的协同过滤推荐算法，引入模糊聚类降低计算复杂性，提高推荐效果；同时通过SMOTE过采样技术改善数据的稀疏性，利用不同用户的历史数据构建用户-项目矩阵，通过对物品的评分计算用户之间的相似性，根据用户之间的相似性预测用户对感兴趣商品的评分，优化时间因子，进而实现推荐。

2.2 用户-项目评分矩阵和时间矩阵

表1所示为协同过滤推荐算法中的用户-项目评分矩阵R，包含一个用户的集合U=(u1,u2,…,um)和一个项目的集合I=(i1,i2,…,in)，m个用户针对n个项目的评分形成m×n阶评分矩阵，用户uk对项目ij的评分记为rkj。

Table 1 User-item scoring matrix R表1 用户-项目评分矩阵R

表2所示为协同过滤推荐算法中项目的评分-时间矩阵T，包含一个用户的集合U=(u1,u2,…,um)和一个项目的集合I=(i1,i2,…,in)，m个用户针对n个项目的评分时间形成m×n阶评分时间矩阵，用户uk对项目ij的评分时间表示为tkj。

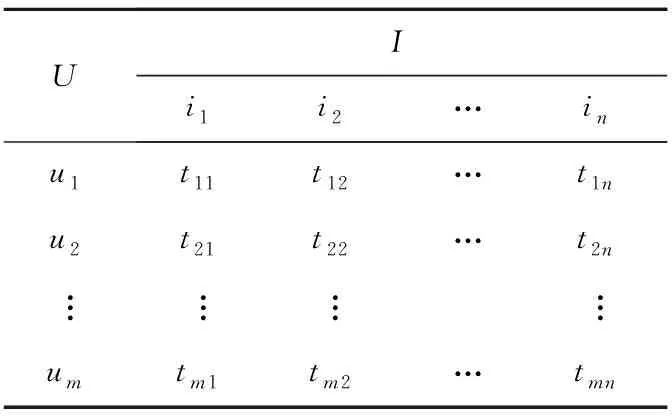
Table 2 User-project time matrix T表2 用户-项目时间矩阵T

2.3 相似性度量和相似矩阵

在用户项目评分矩阵中，为每名用户寻找“特性相同”即有相同评分项的用户，计算用户间的相似性。常用的相似度评价指标有杰卡德系数、欧氏距离、余弦相似度和皮尔逊相关系数等。杰卡德系数通常用于衡量集合间的相似性；欧氏距离注重计算绝对距离，不能体现数据的整体性；余弦相似度侧重方向差异；皮尔逊相关系数解决了各维度量纲的差异性，计算相似度时更侧重于考虑整体性，通过减去用户的均值，实现了对于同一个用户多维度的考察，计算公式如式(1)所示：

sim(uu,uv)=

(1)

表3所示为用户-用户相似矩阵S。本文应用皮尔逊相关系数法计算用户之间的相似度。

Table 3 User-user similarity matrix S表3 用户-用户相似矩阵S

3 带时间参数的协同过滤

“物以类聚，人以群分”，人们总是寻找和自己兴趣相同的用户，把用户分成几个类型。本文选择使用一种基于模糊聚类FCCF(Fuzzy Clustering Collaborative Filtering)的算法，根据用户对项目的评分把用户分成不同的类，每类对应相同兴趣爱好的用户。但是，由于用户评分数据存在严重的数据稀疏问题，使得模糊聚类效果很差。

本文应用SMOTE过采样技术对原数据进行填充，有效解决了稀疏问题。在此基础上提出伴随时间因子的模糊聚类协同过滤推荐算法，首先构造项目评分矩阵，并计算用户相似矩阵，采用模糊聚类对用户进行聚类操作；然后引入时间因子，对用户感兴趣的商品评分进行预测，使得推荐信息更具有实时性。伴随时间因子的模糊聚类协同过滤推荐算法流程图如图1所示。

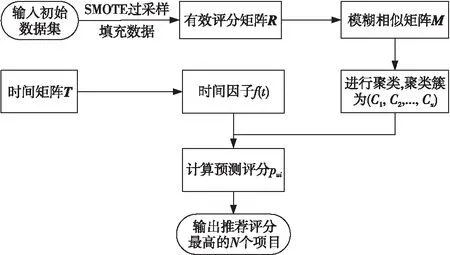
Figure 1 Fuzzy cluster collaborative filtering recommendation algorithm with time of SMOTE图1 伴随时间因子的模糊聚类协同过滤推荐算法

3.1 数据预处理-填充稀疏数据

不平衡数据集是指数据集中某些类样本明显少于其他类[18]。在实际问题中不平衡问题普遍存在，比如文本分类、医疗诊断和天气预测等。SMOTE利用K近邻和线性插值，在相距较近的2个少数类样本间按照一定规则人工插入新样本，使少数类样本增加达到数据平衡,传统的随机采样容易导致过拟合现象，SMOTE针对该现象有很好的改善作用。这种填补缺项数据的技术能够很好地解决数据稀疏问题，同时不影响模糊聚类的分类性质，所以本文应用SMOTE过采样技术对原始数据集进行预处理，生成用户-项目评分矩阵。

SMOTE处理数据的基本思想：数据预处理阶段，为降低数据不平衡度，应用K近邻合成新的数据加入到数据集中，以此填补空白缺项。推荐系统的原始用户评分数据中，给定的评分数据很少，大部分评分缺项，造成严重的矩阵稀疏问题。为了便于讨论，本文规定已评分样本为少数类样本，未评分样本为多数类样本，使用SMOTE过采样技术填充稀疏数据的算法步骤如下所示：

(1)对于少数类样本rui，以欧氏距离(式(2))计算K近邻。针对某一用户的项目ii，计算少数类样本中和项目ii有公共评分的所有用户间的距离，得到K近邻，其中K值默认为5。

(2)

其中,i=1,2,…,n;uu,uv为2个不同的用户

(2)根据项目评分中样本的不平衡比确定采样倍率。对于每一个少数类样本rui,从其K近邻中随机选择L条用户交互记录，并根据式(3)生成新样本ruj：

ruj=rui+rand(0,1)*(rvi-rui)

(3)

其中,u,v=1,2,…,m;i=1,2,…,n;rand(0,1) 表示0～1的随机数。

(3)将新生成的样本全部加入原始数据集中，解决数据的稀疏问题。

3.2 用户-项目评分矩阵的模糊聚类

模糊聚类是利用模糊等价关系将给定对象进行等价类划分，和其他聚类方法不同的是其不需要提前确定聚类数目，通过对分类对象设置阈值进行对象的属性划分，该矩阵满足自反性、对称性和传递性。根据平方法合成传递闭包对元素进行编排，确定阈值，当划分类的数目趋于稳定时确定项目的最终分类。模糊聚类算法FCCF的聚类过程描述如算法1所示：

算法1模糊聚类算法FCCF

输入：用户评分矩阵R。

输出：模糊聚类簇(C1,C2,…,Cx)。

步骤1建立用户评分矩阵。

设用户为论域U={u1,u2,…,um}，每个用户对应n种类型电影的评分(表示其爱好)rui,i∈1,2,…,m，得到原始用户有效评分矩阵R=(rui)m×n。

步骤2构建模糊相似矩阵可以采用贴近度法、距离法和相似系数法，本文采用相似系数法中的皮尔逊相关系数建立模糊相似矩阵M，主对角线上的元素都为1，其他位置元素用皮尔逊相关系数计算得到，构成的对角矩阵如式(4)所示：

u≠v

(4)

步骤3用平方法合成传递闭包，建立模糊等价矩阵t(M)，M∘M=M2，M2∘M2=M4,…，总能找到一个q使得Mq∘Mq=M2q。

(5)

式(5)是M的传递闭包，并将t(M)中的元素从大到小编排为a1>a2>a3>…>ai，ai为传递闭包中的元素。

步骤4计算当阈值λ=a1,a2,…,ai时，对应不同的截集，即模糊聚类簇(C1,C2,…,Cx)。

3.3 伴随时间因子的用户评分预测

传统的协同过滤推荐算法根据用户的偏好，通过用户的历史记录进行推荐，此过程离线进行[19]，忽略了人的兴趣会受到时间影响，但现实生活中用户对物品的喜爱会随时间发生改变，历史记录与当前评分时间越近，越能代表最近的爱好[20,21]。用户兴趣不断变化但在传统的协同过滤推荐算法中不能体现出来，对用户评分设置统一权重推荐的实时性问题在此时显得尤为重要。根据用户的评价历史，对用户进行实时推荐，王永贵等[22]根据不同的时间段用户的兴趣可能发生变化，引入时间因子TF1(Time Factor 1)(如式(6)所示)，提高了推荐效果。本文在此基础上结合艾宾浩斯遗忘曲线，针对用户历史记录间隔较长的问题，平衡评分时间差，模拟人类兴趣变化改进式(6)，将时间因子TF1优化为TF2(Time Factor 2)，如式(7)所示。使时间因子参与预测评分，不同的评分时刻将会被赋予不同的时间权重，这样可以模拟用户偏好变化，实现实时推荐，为了描述清晰，将公式中参数进行统一。

(6)

(7)

其中，Ti为用户对项目ii评分时对应的时间，T0为用户初次进行项目评分对应的时间，Tn表示用户使用推荐系统的总时长,2种时间因子TF1和TF2都记为函数f(t)，取值为(0,1)。

式(8)所示为用户评分预测计算式，其中加入了时间因子f(t)。

(8)

针对用户ui，只要对ui所在的聚类簇利用式(8)，就可以计算出该用户对感兴趣商品的评分预测值，把预测值高的商品推荐给该用户。可见，经过聚类的协同过滤大大降低了计算量。

4 实验

为了描述方便，将文献[9]基于云模型相似度的用户推荐算法改进记为CM-CF(Cloud Model Collaborative Filtering)算法;将文献[16]改进模糊划分聚类的协同过滤推荐算法记为FCCF算法;使用SMOTE过采样技术预处理的模糊聚类协同过滤推荐算法记为SMOTE-FCCF算法；代入时间因子TF1的模糊聚类协同过滤推荐算法记为SMOTE-TF1-FCCF算法；使用SMOTE过采样技术预处理，代入时间因子TF2的模糊聚类协同过滤推荐算法记为SMOTE-TF2-FCCF算法。下面通过实验进行对比研究，以验证模糊聚类和时间因子对推荐算法的效果。

通过平均绝对误差MAE(Mean Absolute Error )和均方根误差RMSE(Root Mean Square Error)指标，检验近邻个数k和推荐个数N对推荐效果的影响。基于模糊聚类簇(C1,C2,…,Cx)，在聚类簇中确定近邻个数的最优值，进而确定推荐个数。

4.1 数据集

实验使用的数据集是由美国明尼苏达州大学GroupLens项目组创建，其中包括100 KB、1 MB、10 MB 3个规模的数据集。本文使用MovieLens-100k数据集验证推荐效果。数据集包含943名用户对1 682部电影的1 000 000条评分，且数据集的每个用户对电影的评分都是1～5分。数据集上每个评分数据都带有评分时的时间戳(时刻序列值)，用户是初次评价即为T0，对第i个项目评价即为Ti，直接代入公式参与运算。本文构建的数据集用户项目评分矩阵稀疏度为93.7%。

4.2 推荐评价

本文采用检验推荐方法最常用的MAE(平均绝对误差)、RMSE(均方根误差)指标：

(9)

(10)

其中，pi表示预测评分，qi表示实际评分，N表示有N个项目。值越小说明算法性能越好。

为验证SMOTE-TF2-FCCF算法的有效性，本文基于控制变量法设计了2组实验进行测试，同时对过采样倍率进行设置，如果过采样倍率过大，新增样本点的选取范围也会增大，难以寻找真正的近邻用户；如果过采样倍率过小，数据的稀疏度依然很大，难以起到数据填充的效果，因此设置过采样倍率为500%。

4.3 复杂度分析

除了考虑算法的准确性，算法的时间效率也是不容忽视的衡量指标。5种算法计算相似度的时间复杂度都为Ο(m×m)，m为用户数目，相差不大；但加入模糊聚类后评分过程的复杂度为Ο(nk)(n为项目数，k为用户的近邻个数)，其余4种传统的项目评分过程的复杂度为Ο(m×n)，一般地有m>>k，所以本文算法通过模糊聚类搜索近邻用户，大大缩短了推荐的时间，保证了推荐的效率。

4.4 实验设计和结果分析

实验环境为：

操作系统为Windows 10 x64,处理器为Intel(R) Core(TM) i5-8250U CPU @ 1.60 GHz 1.80 GHz,RAM为12 GB。

语言环境为gcc version 8.2.0, Python 3.7.5。

4.4.1 CM-CF算法、FCCF算法和SMOTE-FCCF算法的对比

A组实验是CM-CF算法、FCCF算法和SMOTE-FCCF算法在MovieLens-100k数据集上测试模糊聚类的效果，分别通过云模型、模糊聚类和加入SMOTE过采样技术填充的模糊聚类，以MAE和RMSE作为检验算法准确性的评价指标，进行3种算法的对比。

A组实验结果如表4所示，设置聚类数的取值为1～500，间隔为1，在MAE值最低点时确定聚类数，求得RMSE值。观察类簇中用户的个数多集中于[20,60],以递增间隔为2，此时3种算法的最近邻k的最优取值分别为40，50，26。推荐个数N的最优取值分别为8，5，7。

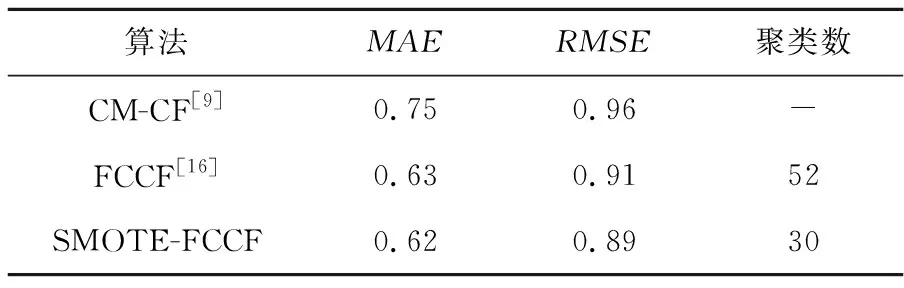
Table 4 Experimental comparison of cloud model recommendation and fuzzy cluster recommendation表4 云模型推荐与模糊聚类推荐实验对比

可以看出CM-CF算法的MAE值最小,为0.75，RMSE为0.96；FCCF算法在聚类数为20时，MAE值最小,为0.63，RMSE为0.91；FCCF算法较CM-CF算法的MAE、RMSE和聚类数均相对较小，表明模糊聚类确实可以提高推荐的准确性。SMOTE-FCCF算法在聚类数为30时，MAE值最小,为0.62，RMSE为0.89，SMOTE-FCCF算法的MAE、RMSE比FCCF算法的也小，说明SMOTE过采样填充优于平均值填充，本文提出的经过数据预处理后的模糊聚类协同过滤推荐算法SMOTE-FCCF优于文献[9]和文献[16]提出的算法。

4.4.2 SMOTE-FCCF算法、SMOTE-TF1-FCCF算法和SMOTE-TF2-FCCF算法对比

为了验证加入时间因子和改进时间因子的有效性，将SMOTE-FCCF、SMOTE-TF1-FCCF和SMOTE-TF2-FCCF算法进行对比，采用MAE和RMSE检验算法准确性。B组实验结果如表5所示。聚类数目通过数据预处理进行模糊聚类确定，与时间因子无关，所以B组实验和A组实验中SMOTE-TF2-FCCF的聚类数目相同，都为30，3种算法只是验证时间因子的效果，故聚类数、最近邻数k、推荐个数N的最优取值都为30，26，7。

Table 5 Experimental comparison of influence of time factor表5 时间因子影响实验对比

横向比较，SMOTE-FCCF的MAE和RMSE分别为0.62和0.89。加入时间因子TF1，SMOTE-TF1-FCCF的MAE和RMSE分别为0.61和0.88,MAE和RMSE较SMOTE-FCCF算法明显降低，可以发现，加入时间因子TF1可以提升推荐效果，而加入时间因子TF2后，SMOTE-TF2-FCCF算法的MAE和RMSE分别为0.60和0.76,该值优于SMOTE-TF1-FCCF算法的，推荐效果大大提高。

纵向比较3种算法的MAE和RMSE值，SMOTE-TF1-FCCF和SMOTE-TF2-FCCF算法的结果都优于SMOTE-FCCF算法的，说明人们的兴趣会随时间的迁移而发生变化，改进的时间因子TF2明显优于TF1,说明改进平衡时间因子有效，可进一步提高推荐算法的推荐性能。

5 结束语

协同过滤推荐算法最大的优点是对推荐对象没有特殊的要求，能够有效地使用其他相似用户的反馈信息。基于模糊聚类的协同过滤推荐算法大大减少了运算量，但也带来了数据稀疏问题。

本文提出伴随时间的模糊聚类协同过滤推荐算法SMOTE-TF2-FCCF，根据用户之间的评分差异，对数据进行预处理，采用SMOTE过采样技术进行填充，有效解决了数据稀疏性问题；利用模糊聚类减小相似用户集合，降低计算复杂度，同时在聚类簇上加入用户评级项目的时间因子，考虑了推荐的实时性。实验结果表明，经过SMOTE过采样预处理的模糊聚类协同过滤算法优于其他数据预处理方法，伴随时间的模糊聚类协同过滤算法优于没有时间因子的推荐算法，而本文改进的SMOTE-TF2-FCCF算法性能最好。

模糊聚类算法对数据稀疏性非常敏感，在未来的工作中，将对改进稀疏度的方法做进一步研究，或者使用对数据没有限制的新的聚类方法，以进一步提高推荐算法的性能。