基于标签共现关系的多标签特征选择*

李雨晨,魏 巍,2,白伟明,王 达

(1.山西大学计算机与信息技术学院,山西 太原 030006;2.山西大学计算智能与中文信息处理教育部重点实验室,山西 太原 030006)

1 引言

在经典监督学习中，每个样本仅拥有一个标签，但是，在许多实际应用中，一个样本通常同时与多个概念相关联[1,2]。例如，艺术界报道《冰雪奇缘》电影的新闻可以与艺术、动画和电影这3个关键字相关联；一幅关于小鹿的图像可以与树木、小鹿和绿色这3个关键字相关联。由此可知，每个样本可以拥有多个标签。这类关于多标签分类任务的研究正受到越来越多的关注[3 - 7]。

在许多实际应用中，多标签数据通常具有成千上万的特征，其中许多特征对于给定的学习任务而言是多余的或无关紧要的，并且高维数据可能会给学习算法带来很多问题，例如计算量大、拟合过度和性能差等。因此，需要进行特征选择，以减轻维数的困扰[8]。

目前，多标签特征选择已经有了许多研究。Zhang等人[9]利用基于主成分分析的特征提取技术去除多标记数据中的不相关和冗余特征，然后利用遗传算法进行特征选择。Zhang等人[10]提出了具有标签特定特征的称为LIFT的多标签学习方法。Xu等人[11]对LIFT进行改进，通过与模糊粗糙集结合构造了多标签学习方法FRS-LIFT。后来，Weng等人[12]提出了一种称为LF-LPLC(multi-label learning based on Label-specific Features and Local Pairwise Label Correlation)的多标签学习新方法，该方法主要关注了标签的功能和局部成对标签相关性。Kashef等人[13]借助Pareto优势概念从多目标优化域中选择最显着的特征。

近年许多研究人员将粗糙集理论[14]用于多标签学习[15]。Lee等人[16]基于互信息提出了适合多标签数据的方法，即通过信息增益的方法来度量多标签的特征选择的重要度。除此之外，度量特征重要度的方法还有许多，比如模糊粗糙集运用模糊熵来进行度量，邻域粗糙集借助邻域粒来进行度量[17]。为了有效减少动态数据中的冗余计算，有效利用之前所获得的有用信息，Liu等人[17]在邻域粗糙集模型的基础上，通过在线流特征选择算法来处理特征动态增加的多标签数据。Qian等人[18]在邻域粗糙集模型基础上，提出了一种基于标签分布和特征互补的多标签特征选择算法。Sun等人[19]针对多标签邻域决策系统，提出了一种基于二值粒子群算法和基于勒贝格测度的多标签特征选择方法。Qian等人[20]提出了一种基于互信息和标签增强的标签分布特征选择算法。Liu等人[21]提出了一种新的流标签环境下的多标签特征选择算法。

上述特征选择算法均未充分考虑标签之间的关系，针对这一问题，本文设计了一种基于标签共现关系的多标签特征选择LC-FS(multi-label Feature Selection based on Label Co-occurrence relationship)算法，主要工作如下所示：

(1)根据样本标签集中标签共同出现和互斥出现的次数计算样本在标签集下的相似度，进而构造样本关于标签集的模糊关系；

(2)基于标签与特征最大相关和特征集最小冗余的原则，设计基于标签共现度的多标签特征选择算法。

2 基本概念

2.1 多标签决策系统

给定一个多标签决策系统ML={U,A,L}，其中U={x1,x2,…,xn}为有n个样本的非空集合，A={a1,a2,…,am}为有m个特征的特征集，L={l1,l2,…,lk}为有k个标签的标签集。每个样本都有标签，因此都属于L的子集，该子集可以描述为k维向量y=[y1,y2,…,yk]，其中yi=1表示样本x含有标签li,yi=0表示样本x不含有标签li，多标签学习的任务是学习一个函数Z:U→2L。

例如：表1是一个含有5个样本、3个标签和3个特征的多标签数据集，x2={3.4,2.6,4.8,1,1,0}，说明样本x2含有标签l1和l2，但是不含有l3。由此可以看出，多标签数据集中的样本可以有不止一个标签，这就使得多标签学习任务更加困难。

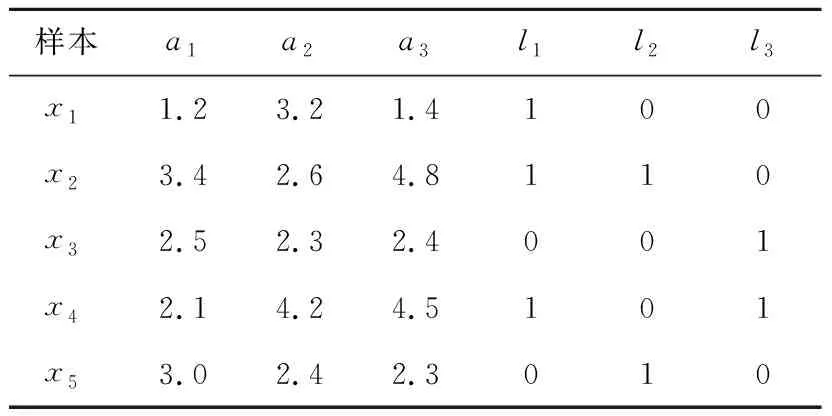
Table 1 A multi-label data set表1 一个多标签数据集

2.2 模糊熵和模糊互信息

对于一个非空的有限样本集U={x1,x2,…,xn}，特征集合为A={a1,a2,…,am},R是定义在U上的一个模糊等价关系，模糊关系矩阵M(R)定义如式(1)所示：

(1)

其中，rij∈[0,1]表示xi和xj之间的关系值，其同样可以记作R(xi,xj),xi,xj∈U。

模糊等价关系R满足以下关系：

自反性：R(x,x)=1,∀x∈U;

对称性：R(x,y)=R(y,x),∀x,y∈U;

传递性：R(x,z)≥miny{R(x,y),R(y,z)}。

给定一个任意的样本集合U,R是定义在U上的一个模糊等价关系,对于∀x,y∈U，关于等价关系的运算如下所示：

(1)R1=R2⟺R1(x,y)=R2(x,y);

(2)R=R1∪R2⟺R(x,y)=max{R1(x,y),R2(x,y)};

(3)R=R1∩R2⟺R(x,y)=min{R1(x,y),R2(x,y)};

(4)R1⊆R2⟺R1(x,y)≤R2(x,y)。

定义1样本xi关于模糊等价关系R的模糊等价类定义如式(2)所示：

(2)

模糊等价类的基数可表示为：

(3)

定义2[22]给定近似空间〈U,R〉,A的模糊熵定义如式(4)所示：

(4)

定义3令A1和A2为A的2个子集，则模糊联合熵的计算公式如式(5)所示：

(5)

其中,[xi]A1∩[xi]A2=min{[xi]A1,[xi]A2}。

定义4令A1和A2为A的2个子集，则模糊条件熵的计算公式如式(6)所示：

(6)

其中,FH(A2|A1)=FH(A1,A2)-FH(A1)。

定义5令A1和A2为A的2个子集，则A1和A2的模糊互信息计算公式如式(7)所示：

(7)

其中,FMI(A1;A2)=FH(A1)-FH(A1|A2)=FH(A2)-FH(A2|A1)。

3 基于标签共现关系的多标签特征选择

3.1 基于标签共现关系的样本相似性

对于某个样本，2个标签同时出现或者同时不出现的次数可以说明这2个标签之间存在某种潜在联系，在本文中，称之为标签的共现度。由于在多标签数据中，许多标签都只是出现在少数样本上，因此对于某个特定的样本，2个标签同时不出现的次数远大于2个标签同时出现的次数，如果直接利用二者之和评价标签的共现度，将会导致2个标签同时出现的次数对共现度的影响很小。为此，需要一个参数α协调2个标签同时出现的次数与2个标签同时不出现的次数之间的关系。根据上述分析，给出标签共现度的定义。

定义6给定多标签决策系统ML={U,A,L}，标签li和lj的共现度定义如式(9)所示：

(8)

根据定义6，进一步给出标签的重要度。

定义7给定多标签决策系统ML={U,A,L}，标签的重要度如式(9)所示：

(9)

定义8给定多标签决策系统ML={U,A,L}，样本的相似性如式(10)所示：

(10)

其中，L(xi)表示样本xi的标签集合。

将基于标签集的样本相似性代入模糊粗糙集模型，可以得到特征与特征之间的相关性以及特征与标签集之间的相关性,如式(11)和式(12)所示：

(11)

(12)

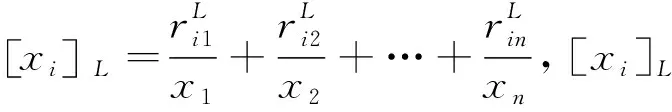
3.2 基于最大相关最小冗余原则的特征选择

本节将基于特征与标签最大相关、特征最小冗余的原则，给出面向多标签决策系统的基于最大相关最小冗余原则的多标签特征选择算法。该算法主要包含2个步骤：

第1步，选择与标签集具有最大相关性的候选特征。令S为已经选择的特征集，L为标签集，则特征集与标签集的相关性定义如式(13)所示：

(13)

根据式(13)容易得到，对于单个特征ai，其关于标签集的相关性为D(ai,L)=FMI(ai;L)。

第2步，选择冗余度最小的特征子集。与标签集相关性最大的特征子集中可能会包括冗余特征(新选择的特征ai与已选择特征集中的某些特征之间有强相关性，或者与已选择特征集中的某些特征组合后与已选择特征集中的其他特征具有强相关性)。为了刻画特征集中特征的冗余情况，给出特征集S冗余度定义，如式(14)所示：

(14)

结合了上述2个定义，给出基于最大相关最小冗余原则的特征选择的特征评价指标，如式(15)所示：

(15)

其中，Sk-1为选择了k-1个特征的特征集合。

式(15)包含2部分，第1部分表示候选特征aj与标签集L之间的相关性，第2部分表示候选特征aj与所选特征Sk-1之间的冗余度。

基于标签共现关系的多标签特征选择算法的具体描述如算法1所示。

算法1基于标签共现关系的多标签特征选择算法(LC-FS)

输入：多标签决策系统ML={U,A,L};/*包含n个样本的非空集合U,m个特征的特征集A,k个标签的标签集L*/

输出：特征集合S。

步骤1初始化S，令S=∅,k=1；

步骤2通过式(8)计算标签间的共现度；

步骤3通过式(9)计算标签的重要度；

步骤4通过式(10)计算样本的相似性；

步骤5 whileA≠∅do

步骤6通过式(15)找到a∈A；

步骤7S=S∪{a}；

步骤8A=A-{a}；

步骤9k=k+1;

步骤10 endwhile

步骤11 returnS。

算法1有2个关键步骤。第1个步骤是分别在特征空间和标签空间中构造模糊关系矩阵，时间复杂度均为O(|U|·|U|)。第2个步骤是搜索特征空间的过程，其时间复杂度为O(|S|·|A|)，其中，|S|是所选特征的数量，|A|是候选特征的数量。因此，该算法的时间复杂度为O(|U|·|U|+|S|·|A|)。

4 实验分析

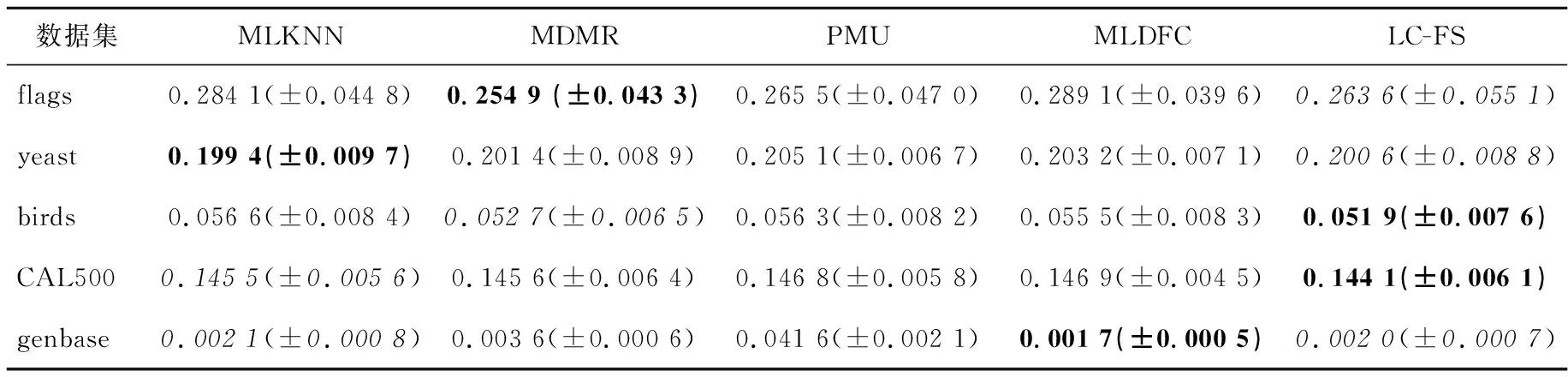
本节将通过实验来验证所提出算法LC-FS的性能。将多标签数据集网站MULAN(http://mulan.sourceforge.net)中的5个数据集(如表2所示)作为实验数据集。在实验中，将MLKNN分类器上得到的结果作为基准，并将2种代表性算法MDMR(multi-label feature selection based on Max Dependency and Min Redundancy)和PMU[23]以及算法MLDFC(Multi-Label feature selection based on label Distribution and Feature Complementarity)[18]作为对比算法。MDMR和PMU算法中特征的评价函数都是采用香农熵度量，MLDFC算法中特征的评价函数采用邻域熵度量。本文算法基于标签共现关系来计算标签重要度时采用了模糊熵的方法。

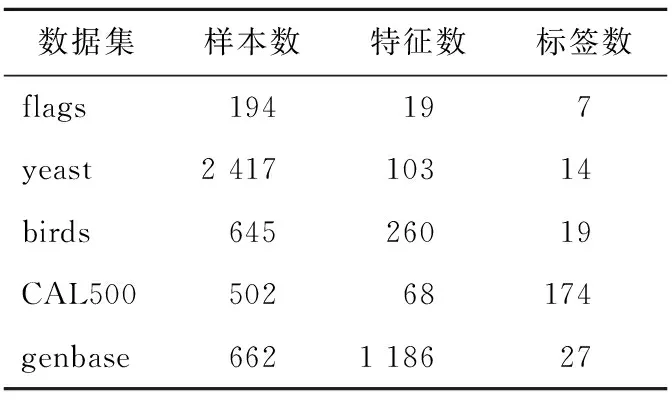
Table 2 Multi-label data sets表2 多标签数据集

4.1 多标签学习评价指标

实验选取了4种常用的多标签性能评价指标[24]。设T={(xi,xj)|1≤i≤N}是一个测试集，其中yi⊆L是真实标签集合，y′i∈L是学习算法的关于样本xi的二进制标签向量，在以下的公式中n表示样本的个数，k表示标签的个数。

(1)AP(Average Precision)：表示预测标签集合中标签的排序等级比实际标签集合中某个特定标签更高的概率，也就是预测标签的平均精度，其计算方式如式(16)所示：

ri(γ)}|)/ri(γ)

(16)

其中,ri(l)代表样本xi预测的标签l∈L的等级。

(2)CV(Coverage)：此度量表示覆盖样本标记的平均距离,其计算方式如式(17)所示：

(17)

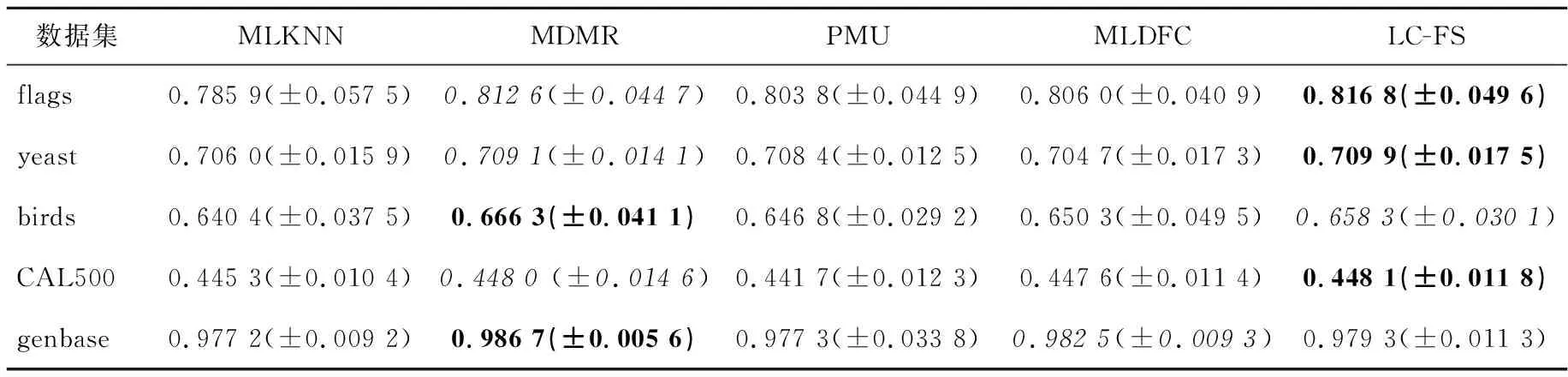
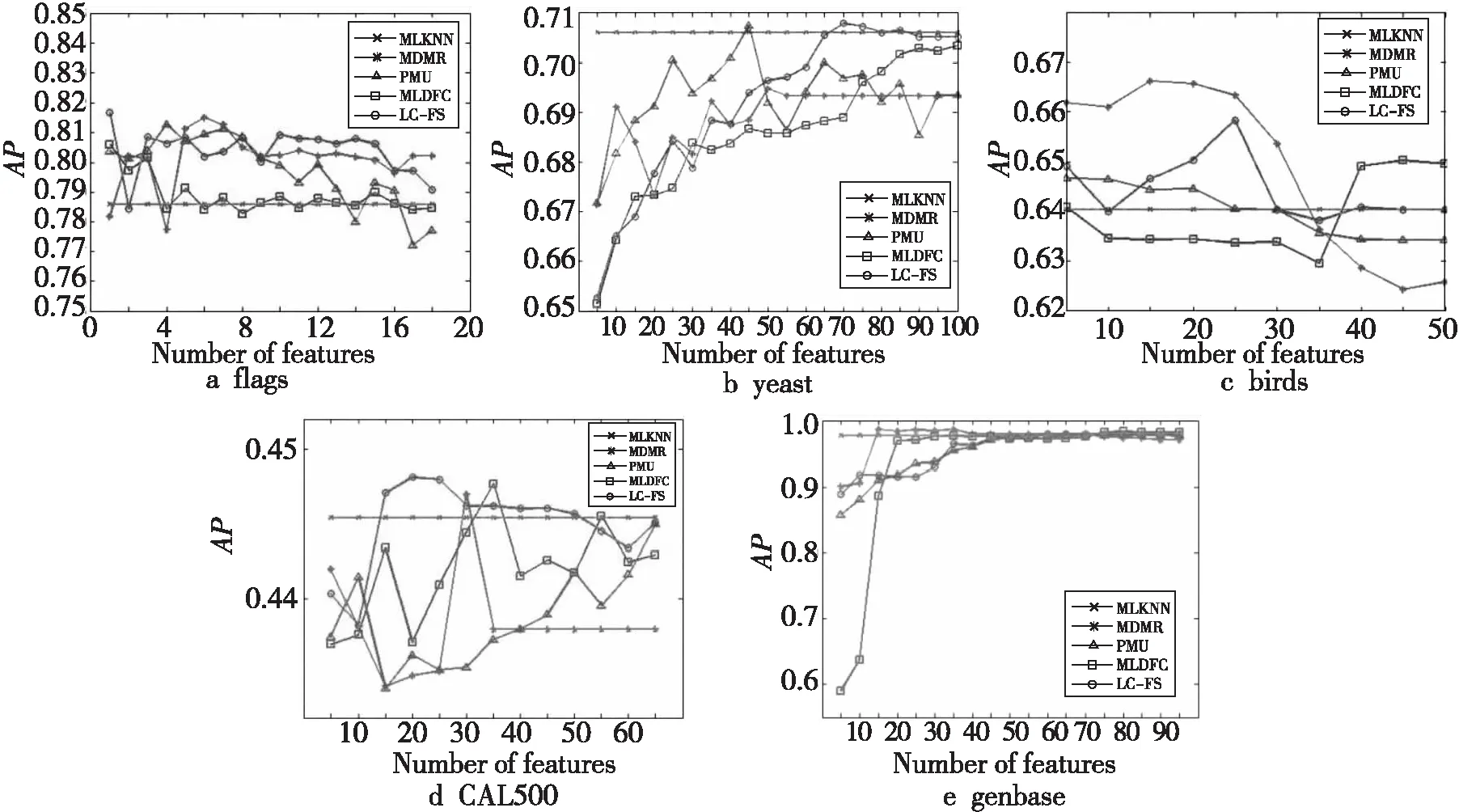
其中,rank(λ)表示标签根据预测概率的排序序号。例如：若λ1>λ2，则有rank(λ1)

(3)HL(Hamming Loss)：表示没有被正确预测的标签比例，即属于样本的标签没有被预测，不属于该样本的标签被预测的比例,其计算方式如式(18)所示：

(18)

其中,⊕表示异或操作。

(4)RL(Ranking Loss)：评估不相关标签比相关标签排序更高的次数,其计算方式如式(19)所示：

(19)

对于以上4种评价指标，平均精度(AP)、覆盖距离(CV)、排序损失(RL)与每个样本的标签排序性能有关，而汉明损失(HL)与每个样本的标签集预测性能有关。

4.2 实验结果

在实验中，利用MLKNN分类器的分类结果，在4个评价指标上比较特征选择算法性能，其中近邻个数K设置为10。在计算标签的共现度时，用到的参数α=10-t,t的取值为[2,8],t以步长1进行遍历，选取使平均精度最优的α。验证方法是10折交叉验证法。

实验结果如表3～表6所示，“↑”表示越大越好，“↓”表示越小越好，±表示方差，最后一列表示本文算法LC-FS的实验结果，其中粗体表示最优值，斜体表示次优值。图1为5个算法在不同的数据集上的精度对比，横轴表示所选特征子集中的特征数量，纵轴表示特征子集对应的分类精度值。

Table 3 Comparison of AP of different algorithms(↑)表3 不同算法在平均精度上的比较(↑)

Table 4 Comparison of CV of different algorithms(↓)表4 不同算法在覆盖距离上的比较(↓)

Table 5 Comparison of HL of different algorithms(↓)表5 不同算法在汉明损失上的比较(↓)

Table 6 Comparison of RL of different algorithms(↓)表6 不同算法在排序损失上的比较(↓)

Figure 1 Comparison of AP of each algorithm on different data sets图1 各算法在不同数据集上的精度对比

从实验结果可以看出，本文算法LC-FS在5个数据集上的实验效果都比较好。具体情况如下：

(1)在flags数据集上，基于LC-FS算法的特征选择结果在3个评价指标AP、CV、RL上都是最佳的。

(2)在birds数据集上，LC-FS算法有着最高的HL，最低的CV和RL，在AP上仅次于MLKNN。

(3)从评价指标AP和CV的角度看，LC-FS算法的性能最好，在3个数据集上都得到了最优值，还有一个次优的结果。

(4)从评价指标RL看，LC-FS算法的性能相对较差，得到了2个最优的结果，不过RL值与最优值差距也均在0.01内，差距并不大。

综上所述，LC-FS算法在上述对比指标下均有不错的表现。

5 结束语

本文提出了基于标签共现关系的多标签特征选择算法LC-FS。在该算法中，首先通过标签的共现度评价标签的权重，进而得到样本在标签集下的相似性，然后基于模糊粗糙集模型计算特征与标签的相关性、特征集的冗余性，并利用最大相关最小冗余原则实现特征选择。实验结果验证了本文算法的有效性。