一类连续的K-means 等价聚类模型及其优化算法*

谢 挺,刘瑞华,魏正元

(1.重庆理工大学理学院，重庆 400054； 2.重庆理工大学人工智能学院，重庆 400054)

1 引言

随着计算机和互联网技术的迅猛发展和快速普及，特别是信息数字化、移动终端和云计算等应用领域的不断扩大，各行业所采集的数据量都呈爆炸式增长，时时刻刻都产生着高维的海量数据，人们正进入一个以“大数据”为代表的人工智能新时代。这意味着传统的计算和分析极限不断受到挑战，这也意味着亟需探索新的数据处理技术和方法，这更意味着数据和信息科学发展的新机遇。聚类作为一种非监督学习方法，是数据分析领域的重要研究内容之一。聚类分析是指利用相似性度量将数据划分为不同的类以发现其中隐藏的结构特征并提取有效信息的过程，其中同一类数据点具有最大相似性，不同类数据点具有最小相似性[1]。聚类分析被广泛应用于模式识别、机器学习、图像处理和人工智能等领域。

K-means算法是一类基于划分的聚类算法，以欧氏距离作为相似性度量，其主要思想是最小化类内数据点到聚类中心的欧氏距离的平方和。从本质上讲，K-means 是一个组合优化问题，具有NP复杂度，主要适用于服从Gauss分布的数据集的聚类。因其简洁性和有效性，K-means仍是当前广泛使用的聚类算法，是十大经典数据挖掘算法之一[2]。具体模型可以描述为：对于给定原始数据X={x1,x2,…,xn}∈Rm×n，其中n是样本点数，m是样本点维数，模型如式(1)所示：

(1)

为使K-means能够应用于大数据聚类分析，本文结合大数据问题中普遍存在的稀疏性要求，从聚类问题的本质出发，设计了一种与K-means等价的连续的聚类模型；同时利用交替方向乘子算法ADMM(Alternating Direction Method of Multipliers)[8]框架构造了其优化算法，分析了算法的收敛性问题并通过数值算例进行了验证。

论文的组织结构如下：第2节将从聚类矩阵出发，设计一种与K-means等价的连续聚类模型；第3节讨论了该模型的性质及其改进；第4节给出了该连续模型的ADMM 算法框架及收敛性分析；第5节利用数值算例来验证模型的高效性和可行性；最后进行了总结。

2 非凸连续的K-means等价聚类模型

聚类问题由指派问题演变发展而来。指派问题是指：有n项任务要由n个人来承担，每项任务只能由1人承担且每个人只能承担1项任务，dij表示第i个人承担第j项任务的成本，Lij=1或0表示第i个人承担或不承担第j项任务，i,j∈{1,2,…,n}，具体描述为:

(2)

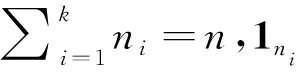
(3)

分析聚类矩阵L不难发现其具有以下属性：(1)非负性，即Lij≥0；(2)稀疏性，即‖Lj‖0≤N,其中N为给定正整数；(3)正交性，即当i≠j时，2列向量内积〈Li,Lj〉=0；(4)随机性，即∑iLij=|Cj|=nj，∑jLij=1。

2.1 非凸连续的等价优化模型

根据K-means聚类算法的模型(式(1))及Lloyd迭代算法，可得聚类中心点为(j=1,2,…,k)：

(4)

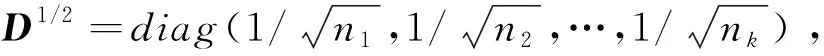
XLD=(c1,c2,…,ck)

(5)

利用向量2-范数和矩阵F-范数间的关系,K-means模型基于欧氏距离时可等价表示为式(6)：

(6)

其中，‖·‖F表示矩阵的F-范数，为矩阵各元素平方和的二次方根。又由于矩阵L和D之间的关系，可设M=LD1/2，则有LDLT=LD1/2D1/2LT=LD1/2(LD1/2)T=MMT，将其代入式(6)中有：

(7)

由矩阵M的定义、式(7)及聚类矩阵的非负、随机和正交性，可设计模型(1)或模型(7)中K-means问题的等价连续形式，如式(8)所示：

s.t.MMT1n=1n,MTM=Ik,M≥0

(8)

其中，M≥0表示M中所有元素不小于0。

由于稀疏是大数据聚类问题的本质属性，为进一步突出稀疏性以提高聚类效果，还可以构造如式(9)所示的等价连续形式：

s.t.MMT1n=1n,MTM=Ik,‖M‖0≤N

(9)

其中，M∈Rn×k，1n表示含有n个1元素的n维列向量，Ik为k阶单位矩阵，N为稀疏约束常数。

可以看出，模型(8)中的目标函数F是关于矩阵变量M连续的四次函数，随机约束和非负约束集为凸，而正交约束集非凸。在此需要特别指出的是，我们注意到有许多文献讨论了K-means算法模型的变换形式，包括其与矩阵分解[9,10]、SVD(Singular Value Decomposition) 分解[11]、非负矩阵分解[12,13]等之间的联系，但这些讨论都仅仅停留在通过数学推导在模型的数学表达式上给出一种解释，其所得到的变换模型既求解困难也没有良好的聚类性质。例如，文献[9]中所给出的K-means等价模型，不论是目标函数还是约束条件都极其复杂，根本无法求解和应用。

2.2 等价模型的性质与特点

根据模型的目标函数形式，K-means聚类问题可以看成原始数据X的低秩逼近，也可以看成原始数据X的降维自表示。本节将利用3个定理描述模型(8) 和模型(9) 的良好聚类特性和等价性问题。

定理1等价聚类模型中的矩阵变量M具有如下性质：

(1)Rank(MMT)=k;

(2)λ(MMT)∈{1,0};

(3)‖MMT‖1=n。

证明(1)由于MTM=Ik，则Rank(MTM)=k。又由Rank(MTM)=Rank(MMT)，则有：Rank(MMT)=k。

(2)由于MTM=Ik，即矩阵MTM有k个特征值且都为1。又由矩阵MTM与MMT互为转置，则2个矩阵有相同的非零特征值，从而MMT的特征值为：λ(MMT)∈{1,0}。

(3)根据模型约束条件MMT1n=1n，以及1-范数的性质，有：‖MMT‖1=‖MMT1n‖1=‖1n‖1=n。

□

定理2若记类Ci中的数据点和聚类中心分别为XCi和ci，则对于任意数据点x∈X都有如下等式成立：

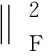
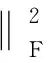
(10)

证明由F-范数性质有：

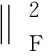
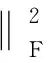
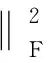
(11)

又由于聚类中心点的定义有：

|XCi-ci1ni|=

(12)

故等式成立。

□

定理3若矩阵M∈Rn×k满足模型(8)中的约束条件，当且仅当M为聚类矩阵。即非凸的连续优化模型(8)与K-means模型等价。

证明充分性。由于M=LD1/2，可知M满足MMT1n=1n,MTM=Ik,M≥0 此3个约束条件，即充分性成立。

必要性。当M满足MTM=Ik，表明M为列单位正交矩阵，即其任意不同2列内积〈Mi,Mj〉=0。由M≤0，可得矩阵M的每一行至多只有1个非零元素。此外又由于MMT1n=1n，可得矩阵M的每一行至少有1个非零元素。综合以上2方面可得，M的每一行有且仅有1个非零元素。为方便描述，设矩阵M不同列上的非零元素依次为α1,…,αn1,β1,…,βn2,…,γ1,…,γnk，即(相似)矩阵M如式(13)所示：

(13)

将M表达式代入MMT1n=1n，可得如下关于参数αi方程组：

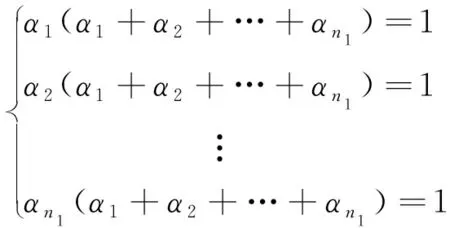
(14)

□

从定理1和定理3可以看出，聚类矩阵的随机性、非负性和正交性是其基本属性。聚类的过程不仅是降维的过程，也是数据的线性表示过程。因此，从聚类矩阵出发而构造的连续、非凸的K-means聚类算法的模型和原始K-means 聚类算法的模型是一致的，具有相同的聚类结构和聚类效果。定理2表明在聚类矩阵上，三角不等式的等号成立，进一步解释了聚类矩阵的空间结构。

3 非凸连续等价模型的优化算法

当前大数据聚类问题是大数据分析的主要手段，其快速算法的研究是一个非常重要的课题[5,14,15]。前文已经指出：与相关文献中的等价模型不同的是，本文给出的等价模型不仅是离散问题的连续化而且具有快速解法。在此，本节主要利用ADMM的迭代格式针对聚类等价模型讨论其优化算法。因为模型(8)可以类似于模型(9)导出算法格式，下文仅就模型(9)的算法形式进行推导。

3.1 基于ADMM的优化算法

按照常用的罚函数法，可以将模型(9)中的3个约束条件松弛到目标函数中。对于其中的稀疏约束，即求解困难的L0范数问题一般将其松弛为L1或L2范数。不失一般性，本文将稀疏约束松弛为L1，可得模型(9)的罚函数为：

(15)

其中α,β,γ0为对应的罚参数。若令:

(16)

(17)

其中,α1T为在矩阵X下方添加一行元素全为α的n维行向量，则式(15)可以转化为：

(18)

将变量分裂，令Z=M，则式(18)可写为：

s.t.M-Z=0

(19)

其中有2个变量M和Z，可以利用ADMM算法[8]框架求解模型(19)。该问题的增广拉格朗日函数如式(20)所示：

(20)

其中,Λ为对偶变量。由式(20)可得ADMM的迭代格式如式(21)～式(23)所示：

(21)

(22)

Λ←Λ+μ(M-Z)

(23)

其中需要求解关于M和Z的2个子优化问题。

首先求解关于M的子问题。若记：

(24)

(25)

则：

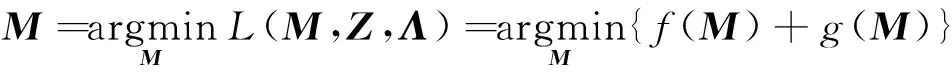
(26)

将f(M)在M=S点进行二次近似展开，则有：

(27)

其中,θ=λmax(YTY+ZZT)。利用邻近点梯度法，M的子问题可转化为如式(28)所示形式：

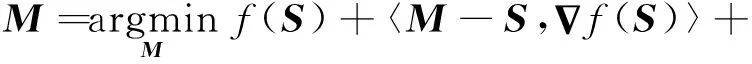
(28)

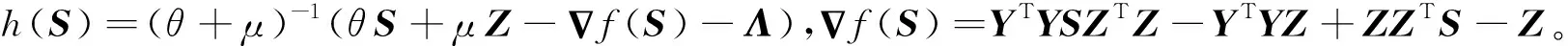
利用快速迭代收缩阈值算法FISTA(Fast Iterative Shrinkage Threshold Algorithm)计算式(28)有：

(29)

其中，shrink{U,v}=sign(U)max(|U|-v,0)，|U|表示U中每个元素的绝对值。具体迭代形式可以展开如式(30)所示：

(30)

其中，Mk和Sk分别是M和S的第k次迭代值。

接下来求解关于Z的子问题。由式(21)～式(23)可以看出关于Z的子问题:

(31)

(32)

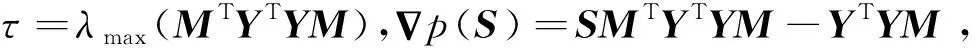
(33)

由式(33)可得Z的解为:

Z=(MMT+(τ+μ)In)-1((1+μ)M+

(34)

综上可得非凸连续等价优化模型的快速优化算法如算法1所示。

算法1基于ADMM的连续等价优化模型的快速优化算法

输入：X∈Rm×n,k=0,α,β,θ,μ,τ,γ>0;t1=1,M1=0,Λ1=0,S1=0。

输出：M,Z,Λ∈Rn×k。

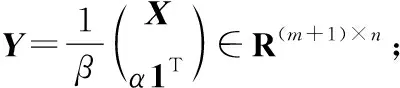
步骤2While不收敛do

k←k+1;

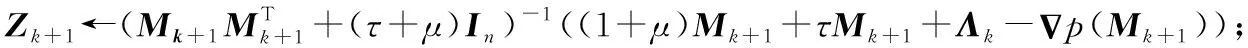
Λk+1←Λk+μ(Mk+1-Zk+1);

Endwhile

步骤3输出Mk+1,Zk+1和Λk+1。

3.2 算法的收敛性分析

另一方面，对于非凸的优化问题需要有针对性地设计不同算法，一般情况下难于找到其全局最优解，大部分情况都是局部最优解甚至是可行解。对于本文中给出的算法1也可以得到类似结论[5,7,8]。

证明如果Q=(W,Z,Λ)为模型(6)的KKT点，则其应满足式(35)：

M-Z=0

(35)

由于Qk→Q，即Wk→W,Zk→Z,Λk→Λ。由算法1，当Λk→Λ时可得M-Z→0，即M-Z=0。 又由式(28)和式(33)中的一阶条件，可得:

Z(ZT-Ik)+μ(M-Z)+Λ+∂‖M‖1,

M(MTZ-Ik)+μ(Z-M)-Λ,

(36)

□

4 数值算例

为比较本文的连续等价模型的优化算法和经典的K-means算法在数据聚类上的表现，将在人造数据和Yale Face Database[16]上开展数值实验。人造数据为：随机选取m维空间中的k个点作为聚类中心点，分别以这些聚类中心点构造方差均为σ的高斯点，并使得这些所有的点的总数为n，在算例中选取(m,k,n)=(325,10,3000)，方差依次选取σ=(2.7,2.8,3.0,3.2,3.3)。Yale Face Database包含11个不同个体的不同面部表情和神态图像，每人15幅，共165种灰度图；在人造数据算例实验中选取的聚类数依次为k=(6,8,10,12)。本节所得的结论都是在Intel Core i7-3770 CPU 3.40 GHz, 8 GB RAM，Matlab R2017b的环境下运行得到。

本节主要是从运行时间和聚类精度来比较2类算法。运行时间以秒(s)为单位；聚类精度则选择常用的聚类精度函数AC，通过比较聚类指标集L和真实指标集T之间的差距得到，其定义如式(37)所示：

(37)

其中，Ti∈T,Li∈L分别表示第i个元素的真实指标和聚类指标。当x=y时，δ(x,y)=1；当x≠y时，δ(x,y)=0。一般利用百分比表示AC函数，详见参考文献[4,5,15]。传统的K-means算法利用Matlab工具箱中的嵌入函数，连续等价模型利用基于ADMM的迭代算法，其中参数的选取参照文献[8]。因为K-means对初始值极其敏感，为使得对比更加公平，取20次计算的平均时间和平均聚类精度进行对比。此外，在每次计算时选取30个不同的初始值进行运算，并将最小目标函数值作为该次的计算结果。详细结果如表1和表2所示。通过表格对比可以看出，本文所提出的等价连续模型的优化算法不论在聚类时间还是聚类效果上都明显优于经典的K-means聚类算法。

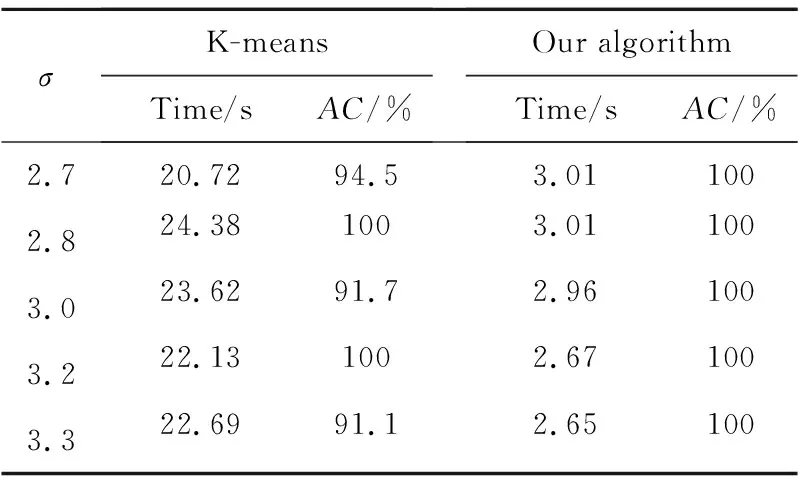
Table 1 Results of numerical experiments on artificial data表1 人造数据上的数值实验结果

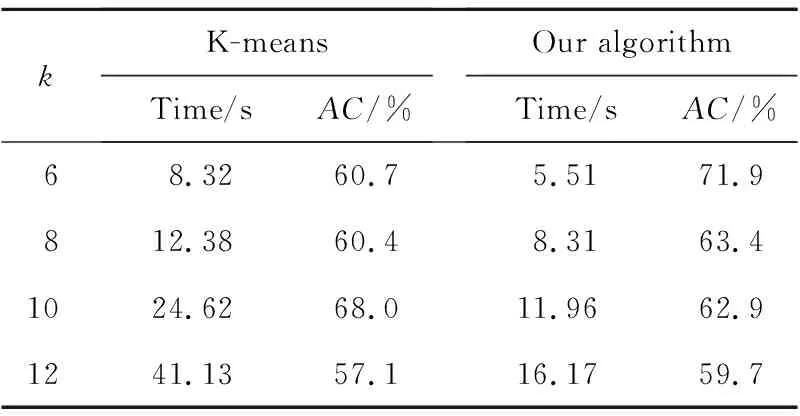
Table 2 Results of numerical experiments on Yale Face Database表2 Yale Face Database上的数值实验结果

5 结束语

本文将经典K-means模型进行矩阵化处理，并结合聚类的本质属性提出了一类非凸的连续优化模型。基于ADMM算法给出了该模型的迭代算法，并从理论上讨论了解的收敛性问题。通过人造数据和人脸数据验证了该算法相比经典的K-means算法在聚类时间和聚类效果上的极大提升。所提模型和算法克服了传统K-means的计算瓶颈，为解决大数据聚类中的相关问题提供了一个途径。但是，本文给出的算法参数较多，针对不同的问题需要调试参数，这需要进一步进行研究简化。