一种基于混淆矩阵的多分类任务准确率评估新方法*

张开放，苏华友，窦 勇

(国防科技大学计算机学院， 湖南 长沙 410073)

1 引言

在机器学习领域，多分类任务[1 - 3]是指将样本实例分为3个及以上类别之一的问题(将样本实例分类为2个类别之一称为二分类)。由于分类算法和模型的局限性，对分类器的分类结果进行准确性评估是一个必须面对的问题[4,5]。另一方面，由于分类器过拟合现象的存在，恰当地选择准确率评价指标显得十分重要。现有的一些评价指标，诸如准确率[3]、Kappa系数[6]和F1值[3]等，都是基于混淆矩阵对总体分类效果进行的评估。它们很难给出单个类别的分类效果，这在某些实际应用中是不足以满足用户需求的(例如在MNIST(Mixed National Institute of Standards and Technology database)手写字符体识别任务中，数字0出现的概率和重要性往往会比其他数字大和高)。

本文将该方法引入多分类任务模型评估场景。该方法最初运用于地震预测领域[7]，后被引入遥感图像目标识别效果评估领域[8,9]，用于评估识别的效率。本文针对机器学习领域的多分类任务，对该方法进行拓展和迁移应用，并给出了理论推导过程。基于MNIST手写字符体识别和CIFAR-10(Canadian Institute For Advanced Research, 10 classes)数据集的多分类任务实验结果表明，与已有模型准确率评估方法相比，上述方法可以较好地评估模型分类准确率。值得一提的是，同样是基于混淆矩阵进行推理，该方法计算简单，并且可以同时给出分类器整体以及每一个类别的分类效果，对于评估和改进训练过程具有一定的指导意义，同时在特定的任务背景下应用前景广阔。

本文的主要工作如下所示：

(1)提出了一种新的多类别分类效果评价指标，该指标考虑真实标签和预测标签之间的数值差异，可以更好地反映分类模型的分类效果。

(2)从数学上给出了所提指标的理论推导及其性质证明。

(3)通过该指标可同时获得总体和单个类别分类效果，以改进分类模型训练过程。

(4)在不同的应用中评估了各指标在MNIST和CIFAR-10数据集上的分类效果，以验证其有效性和鲁棒性。

2 现有评估方法及其缺陷

本节主要介绍几种常见的模型准确率评价指标及其不足。不失一般性，考虑表1所示的三分类问题的混淆矩阵。表1中，l、m、n分别代表类别1、类别2、类别3的真实样本数，r、s、t分别代表结果中预测为3个类别的样本数；w是所有样本的总数；a、b、c代表被正确分类的样本数，d、f、g、e、i*、h代表被错误分类的样本数。

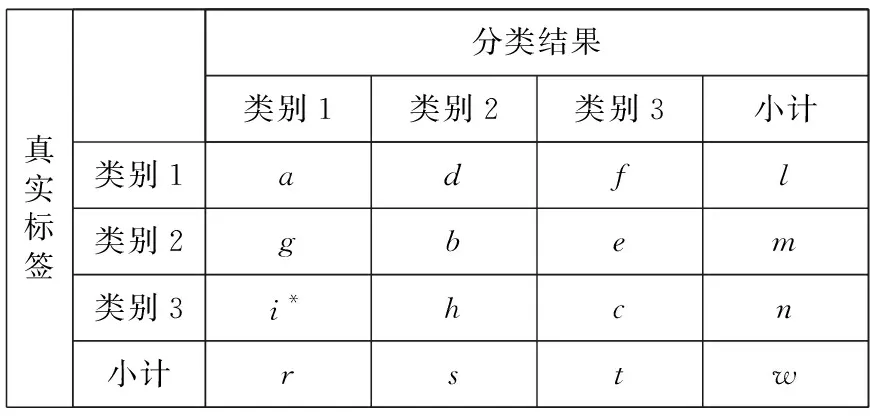
Table 1 Confusion matrix of the three-category task表1 三分类问题混淆矩阵

2.1 准确率

准确率作为分类问题最原始的评价指标，定义为正确预测的样本占总样本的百分比。对于表1所示的混淆矩阵，有：

(1)

显然，这一指标没有考虑非对角线因素，也就是忽略了诸多的边界样本信息，尤其是在各个类别样本数量不均衡的情况下，它不能很好地评估分类效果的好坏。

2.2 PR曲线

PR曲线是描述精准率、召回率变化关系的曲线。其中P代表精准率(Precision)，又叫查准率，是针对分类结果而言的，定义为所有被预测为正的样本中真实标签为正的样本的概率；R代表召回率(Recall)，又叫查全率，是针对真实标签而言的，定义为所有实际为正的样本中被分类为正的样本的概率。曲线最初是针对二分类任务场景提出的，混淆矩阵如表2所示。其中，m、n分别代表类别1和类别2的真实样本数，s、t分别代表分类结果中预测为2个类别的样本数；w是所有样本的总数；a、b代表被正确分类的样本数,c、d代表被错误分类的样本数。表1和表2的a、b、c和d仅有局部意义，分别适用于三分类场景和二分类场景。

Table 2 Confusion matrix of the two-category task表2 二分类问题混淆矩阵

其PR值的计算如式(2)所示：

(2)

对于多分类问题，实际上会获得多组混淆矩阵，也就会得到多组PR值，此时有2种处理方法：宏平均(macro-average)和微平均(micro-average)。宏平均是先计算每个混淆矩阵的PR值，然后再分别取平均；微平均则是计算出全局混淆矩阵的平均正负样本数，然后再计算整体的值。

这样，对于上述三分类问题，采用宏平均方式计算如式(3)所示：

(3)

其中，Pi和Ri分别代表类别i的精准率和召回率,具体计算方法为：P1=a/r,P2=b/s,P3=c/t;R1=a/l,R2=b/m,R3=c/n。

采用微平均方式(对于没有漏检的多分类任务而言，实际就是2.1节中的准确率)计算如式(4)所示：

(4)

可以看出，宏平均虽然加入了更多的非对角线元素，但是仍然只能给出所有类别整体的分类效果，而微平均则和2.1节的准确率等价。同时，PR值是一对此消彼长的统计量，在实际应用中要做好两者的兼顾和取舍。

2.3 F1值

为了解决PR值的上述问题，调和PR值，研究人员提出了F-measure(或F-score)方法，即：

(5)

特别地，当β=1时，认为PR值同等重要，称F1值；有些情况下，如果认为P值更重要，就调整β值小于1；反之，若认为R值比较重要，则调整β值大于1。

虽然F-score给了更大的调节空间，一方面很难根据实际场景量化β值，另一方面仍然无法给出单个类别的分类评估结果。

2.4 Kappa系数

Kappa系数是统计学中的概念，一般用于一致性检验，也可以用来作为衡量分类精度的指标。其计算方法如式(6)所示：

(6)

其中，Po代表总体分类精度(即2.1节中的准确率)，Pe计算方法如式(7)所示：

(7)

其中，rowi和coli分别代表第i个类别的真实样本个数和分类预测的样本个数，具体为：row1=l,row2=m,row3=n;col1=r,col2=s,col3=t。一般情况下，根据Kappa系数大小进行如表3所示的一致性等级划分。

Table 3 Consistency level of Kappa coefficient表3 Kappa 系数一致性等级划分

同样，无法避免的是上述Kappa系数仍然不能给出单个类别分类结果的准确率评估。同时，这种等级划分的适用范围有限，等级划分缺乏一定的合理性，不能适应应用场景的变化迁移和满足用户特定的具体需求。

据作者所知，这方面的工作很少。然而，在一些特定的应用场景中，文献[10-13]进行了一些相关的工作。文献[14,15]研究了评估检索系统的问题，并定义了一些类似于AP(Average Precision)的指标。文献[16-18]通过数学分析和一些特定实验比较了AP和其他一些指标。文献[19,20]提出了一些改进措施，以克服平均精度(mAP)的缺陷。文献[21-23]探究了在其他一些领域改变评价指标的可能性。但是，上述所有工作都只是试图调整或采用AP指数以在某些特定的应用场景中获得更好的性能[24 - 28]。他们很少关注怎样去克服AP及类似指标的固有缺点，且应用场景受限[29 - 32]。

3 R′方法介绍

R方法是由许绍燮院士在1973年提出的，最初运用于地震预测的准确率评估，后来(1989年)给出了更严格的理论推导和证明，并由王晓青研究员等人(1999年，2002年)进行了进一步的改进和推广[7]。Dou等人[9](2004年)将其引入遥感图像分类效果评估，给出了理论推导，并进行了适当改进，称之为R′方法。基于上述原理，这里给出应用于多分类任务场景的评估方法，并仍称之为R′方法。

3.1 方法定义

不失一般性，仍以表2中的二分类问题为例，先给出R′方法的一般原理，然后进行多分类任务的拓展和推广。

以类别1为例，该类别的分类效率R(1)定义如下：对该类别进行正确分类的概率与样本被预测为这个类别的概率之差，如式(8)所示：

R(m|s)=P(s|m)-P(s)

(8)

其中，P(s|m)代表该类别被正确分类的概率，计算方法如下：正确分类的样本数与该类别样本总数之比，如式(9)所示：

(9)

P(s)代表样本被预测为该类别的概率，如式(10)所示：

(10)

同样，P(m)代表这一类别在总样本中的出现概率，如式(11)所示：

(11)

综上，可得：

(12)

进而有：

R(m|s)+P(m)=P(s|m)-P(s)+P(m)=

(13)

根据实际的分类结果，考虑以下3种可能出现的情况：

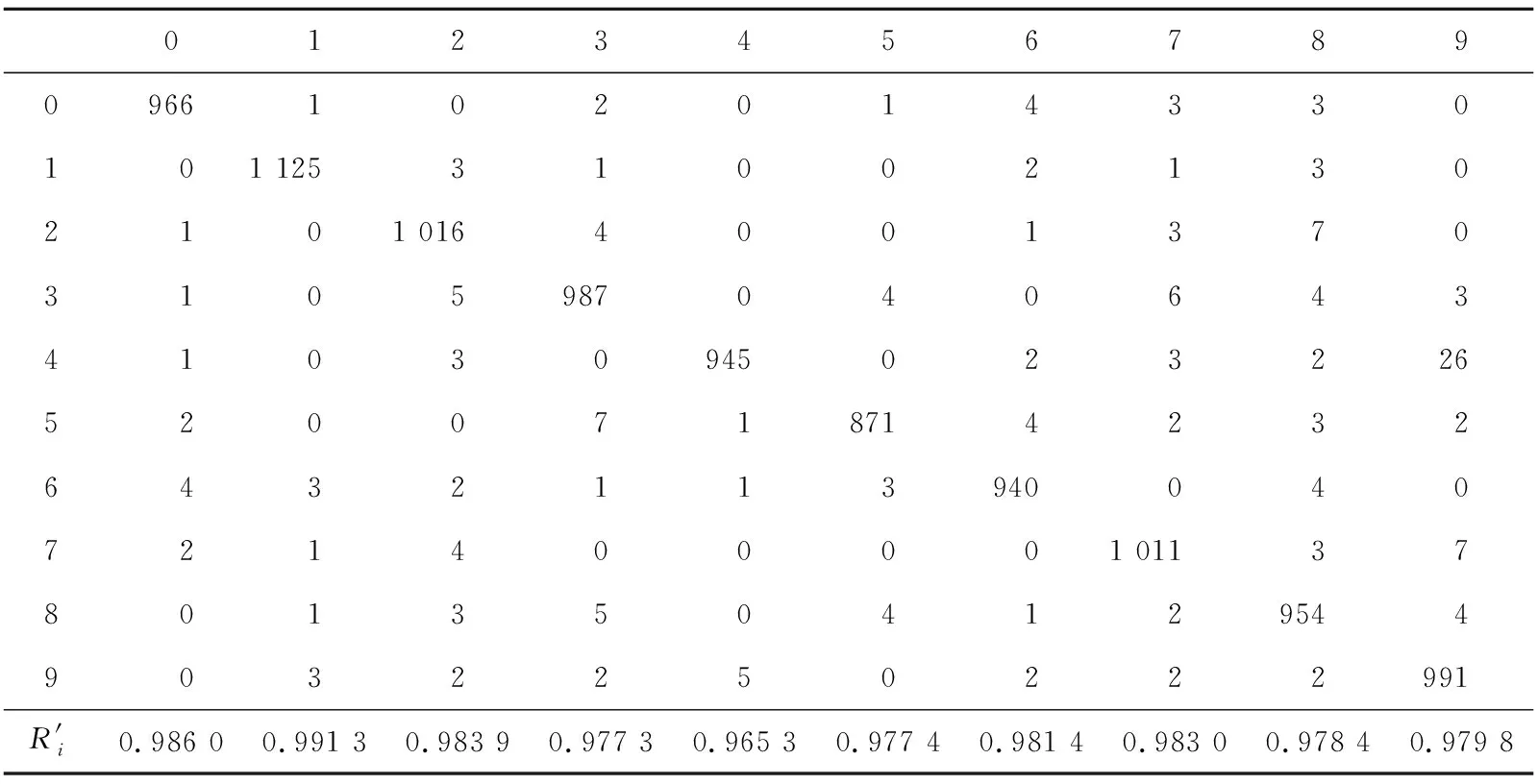
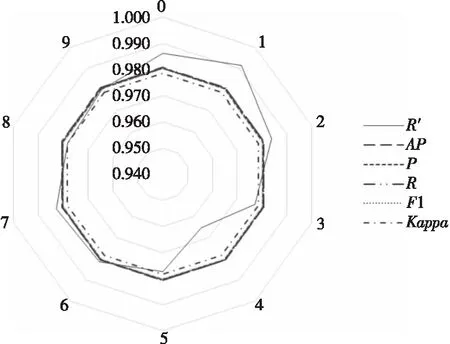
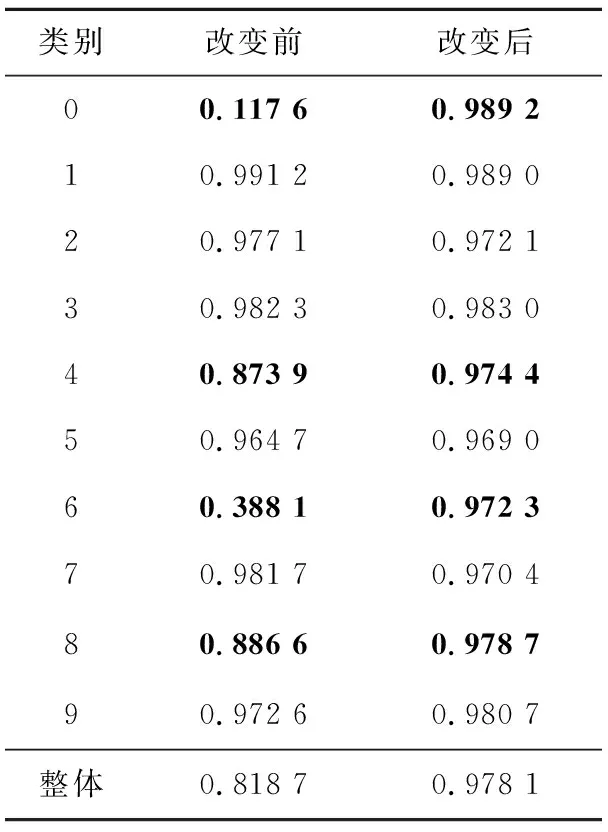
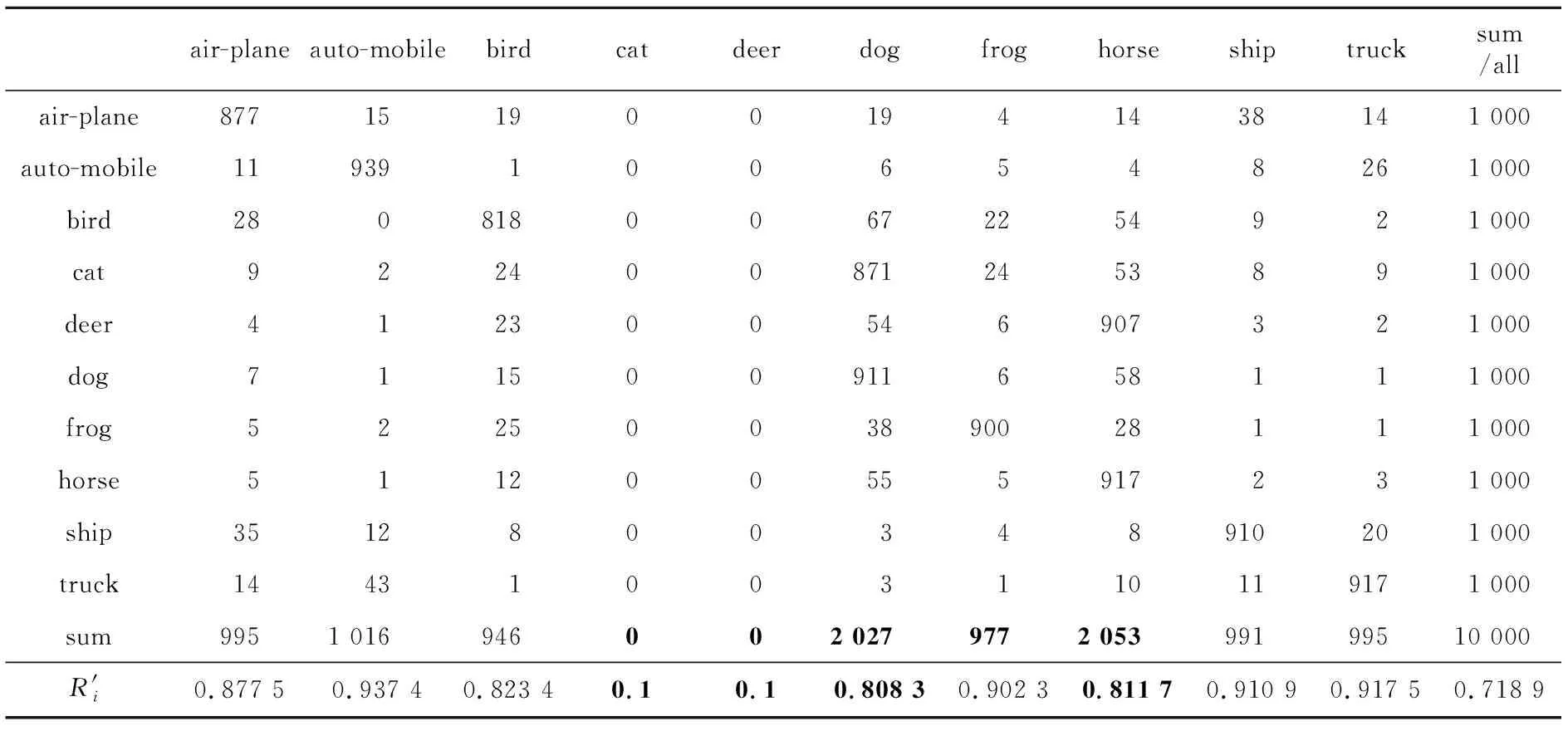
(1)该类别预测样本数小于该类别实际的样本数，即a≤s

(14)

(2)该类别预测样本数大于该类别实际的样本数，即a≤m

(15)

(3)分类结果完全正确，即a=m=s时：

R(m|s)+P(m)=1

(16)

根据R(1)值的定义，可得R(m|s)+P(s)=P(s|m)≥0，即R(m|s)≥-P(s)。所以有：

-P(s)≤R(m|s)≤1-P(m)

(17)

也就是说，R(1)∈[-P(s),1-P(m)]。它越接近于1-P(m)，表明分类效果越好。为方便评估，本文进行以下改进，并定义为R′(1)：

R′(m|s)=R(m|s)+P(m)=

P(s|m)-P(s)+P(m)=

P(s|m)-[P(s)-P(m)]

(18)

这样，R′(1)∈[P(m)-P(s),1]。R′(1)值越接近于1，分类效果越好。

3.2 R′方法在多分类任务下的推广

对于多分类(假设类别数为n)问题，显然不止一个类别需要预测。为此，对上述推理进行以下推广。

设x表示总样本中所有类别真实样本的总数，y代表最终的分类预测结果，xi代表第i个类别的真实样本数量，yi代表第i个类别的预测样本数量，对于机器学习领域的多分类任务而言，每一个样本都会有一个预测标签，所以有：

(19)

基于此，第i个类别分类正确的概率计算如式(20)所示：

P(yi)=P(yi|y)P(y)

(20)

其中，P(yi|y)代表样本被分为第i个类别的条件概率，P(y)代表样本参与分类的概率(对于本文中的多分类任务场景，该概率实际为1)。

进而，对所有类别而言，分类结果和真实标签一致的概率如式(21)所示：

(21)

其中，P(yi|xi)代表第i个类别被正确分类的条件概率。

根据3.1节的结论，对于第i个类别有：

R′(xi|yi)=P(yi|xi)-[P(yi)-P(xi)]

(22)

进而对所有类别而言，有：

R′(x|y)=P(y|x)-[P(y)-P(x)]=

(23)

其中，ai代表第i个类别的样本中被正确预测的样本数量。该值越接近1，表明总体的分类效果越好。

这样，就可以通过这种方法同时获得分类器整体的分类效果评估值R′(x|y)和单个样本分类效果的评估值R′(xi|yi)。在某些应用场景下，用户如果特别关注某一类别的分类效果，可以在保证总体分类效果的前提下，通过调节R′(xi|yi)来满足特殊分类需要。

上文给出了在多分类任务场景下的R′方法。值得注意的是，该方法与Dou等人[9]的R′方法有2点不同：(1)应用场景不同。如式(8)描述的那样，多分类任务场景下，该指标评估每个类别被正确分类的概率，并以样本数作为统计标准。与之不同的是，Dou等人的方法以遥感图像像元的多少表征目标识别概率的高低。(2)适用条件不同。遥感图像识别往往包含像元的错漏现象，也就是某些像元不属于任何一个目标。而在一般的多分类任务场景下，正如式(20)中描述的那样，样本参与分类的概率P(y)=1，也就是不存在样本不被归类的情况。

4 实验及结果分析

本文的实验基于MNIST手写字符体识别任务。这是一个n=10的多分类问题。采用一种典型人工神经网络(LeNet-5)进行训练和测试，得到在测试样本精度最高的参数设置下的测试样本混淆矩阵，并计算出第2节描述的各评价指标，将在4.1节给出，以观察R′方法的评价效果；同时，基于不同超参数设置，给出不同模型下R′值对分类器的评估结果，将在4.2节给出，以评估R′方法的鲁棒性；4.3节通过改变某些样本的容量或者标签，对比在不改变上述容量或者标签的情况下，这些类别的值的变化，以此来进一步验证此方法对于单个类别的评估效果；4.4节则将上述实验迁移到CIFAR-10数据集(对应的神经网络模型采用VGG)并试图从另一个角度说明R′方法的有效性。

4.1 不同评价指标的对比

实验中，测试样本最终在模型(最终测试准确率为98.06%)下得出如表4所示的混淆矩阵(表中行表示实际标签，列表示预测标签；表中同时给出了每个类别的R′值)。基于混淆矩阵，计算得出表5所示的各个评价指标取值(PR值项分别给出P值和R值，用P/R表示)。

Table 4 Confusion matrix of the test samples表4 测试样本分类结果混淆矩阵

Table 5 Evaluation indices of test samples classification result表5 测试样本分类结果评价指标

可以看出，在给定的参数设置下，R′值给出了与现有的评价指标相近的分类器评估取值。值得一提的是，表4说明了R′值可以同时给出整体预测结果的评估指标以及单个类别的评估指标，这是其他指标无法做到的。为进一步说明R′值的上述特性，图1给出了10个类别在不同指标体系下评估结果的雷达图(对于R′值以外的评估指标，由于它们只给出了整体的分类效果评估值，这里对所有类别赋予同样的该评估值)。

Figure 1 Appraised values for different categories of classification results under each indicator图1 各个指标下不同类别分类结果的评估值

同样可以看出，除了R′值以外，其他的评估指标雷达图均为正十边形(每个类别具有相同的全局评估值)。而对R′值而言，可以清楚地看出，实验结果对数字0，1，2，7识别率较高，对数字4识别率最差(数字3，5，6，8，9则介于两者之间)。这给某些场景下的特殊应用需求提供了直观、便利的评估结果和模型选择方法。

4.2 不同分类结果下R′值的对比

为进一步验证R′值的鲁棒性(在不同参数设置下，R′值对不同模型的评价结果有无差异)，本节进行了不同超参数设置(实际是不同学习率)下的10组实验，并对比其分类结果的评估值，如表6(作为参考，同时给出了其他指标的评估R′值；或者更直观地将值绘制为图2的形式)所示。

可以看出，对于不同超参数设置下的分类结果，R′值给出了不同的评估结果。R′值根据不同模型的好坏，给出了其实际效果的评估结果，这说明了R′方法的鲁棒性。

4.3 R′值对单个类别的评估效果

本节的实验采取改变训练样本标签的方法，以此来控制样本容量变化。具体而言，又分为以下2个步骤：首先分别去除类别0和类别6的某些样本，减少类别0和类别6样本的容量，并通过R′方法来评估分类效果，称之为改变前；然后恢复这些训练样本的原始标签，同样通过R′方法来评估分类效果，称之为改变后。

Figure 2 Classifier values under different hyper-parameter settings图2 不同超参数设置下分类器值

改变前后保持模型的其他参数不变。

表7给出了样本标签改变前后各个类别以及整体的R′值。

Table 6 Evaluation values of the classifier under different hyper-parameter settings表6 不同超参数设置下分类器评估值

Table 7 R′ value of each category before and after changing the sample label表7 改变样本标签前后各个类别的R′值

可以看出，在恢复类别0和类别6的样本容量之前(也就是改变前)，他们的R′值很小(分别为0.117 6和0.388 1，如表7中加粗部分所示)，对应的类别4和类别8的R′值也得到一定的影响(分别为0.873 9和0.886 6，如表7中加粗部分所示)。恢复样本原始容量之后(也就是改变后)，类别0和类别6对应的R′值得到显著提升(分别为0.989 2和0.972 3，如表7中加粗部分所示)，对应的类别4和类别8的R′值也得到一定的提升(分别为0.974 4和0.978 7，如表中加粗部分所示)。值得说明的是，这对于优化和改进训练过程具有显著的指导意义，即可以通过观察单一类别或者某一些类别R′值的变化，采取必要的手段(如样本均衡)来改进训练过程。

回到3.2节的关于R′值方法推广。3.2节中给出了某一单个类别的R′值计算方法，如式(22)所示。

考察式(22)，R′值方法在评估分类效果的时候，除了考虑在真实标签中样本被正确预测的概率P(si|mi)之外，还进一步结合了样本被正确预测和错误预测的差异，即P(si)-P(mi)。对于实验中因改变样本标签而导致样本不均衡的情形，这一差异被R′方法很好地提取了出来。

具体而言，考察表8和表9所示的训练样本容量改变前后的测试样本的混淆矩阵。表格中的行表示测试样本真实标签在2次实验中未发生变化，而表示预测标签的每一列则发生了一定的变化(尤其对类别0、类别4、类别6和类别8而言，如表7中加粗部分所示)。这解释了上述实验中这些类别值变化的原因。进一步说，R′方法可以很好地发现和指导解决训练过程中因样本不均衡等原因导致的分类效果评估的差异问题，进而指导和改进训练过程。

4.4 CIFAR-10数据集实验结果

为进一步说明R′方法的有效性和适用性，本节实验采用另一个多分类任务场景的经典数据集CIFAR-10进行验证。

CIFAR-10数据集是一个更接近普适物体的彩色图像数据集，一共包含10个类别的RGB彩色图像：飞机(airplane)、汽车(automobile)、鸟类(bird)、猫(cat)、鹿(deer)、狗(dog)、蛙类(frog)、马(horse)、船(ship)和卡车(truck)。数据集中每幅图像的尺寸为32 × 32，每个类别有6 000幅图像，数据集中一共有50 000幅训练图像和10 000幅测试图像。与MNIST的灰度图像不同，CIFAR-10数据集由3通道RGB彩色图像组成，图像尺寸也比MNIST的28 × 28更大。此外，数据集是现实世界的真实物体，图像噪声更大，物体的比例、特征也都不尽相同，识别难度更大。但是，值得注意的是，CIFAR-10数据集样本更加均衡，每个类别的样本数量都是6 000，这对于进一步验证4.3节实验的设计思路更加方便和有效。

Table 8 Confusion matrix 1 before sample label changes表8 改变样本标签前的混淆矩阵1

Table 9 Confusion matrix 1 after sample label changes表9 改变样本标签后的混淆矩阵1

同样采用4.3节的实验设计方法，通过改变测试样本的标签来模拟样本不均衡的现象(这里将cat类别部分样本去除，将deer类别部分样本去除)。表10和表11分别给出了对应的混淆矩阵(表中同时给出了各个类别和整体上分类效果的评估R′值，表中最后一列的all代表整体分类效果的R′值)。

从表10和表11中可以看出，在恢复类别cat和类别deer的样本容量之前(也就是改变前)，它们的R′值很低(分别为0.1和0.1，如表10中加粗部分所示)，对应的类别dog和类别horse的值也受到一定的影响(分别为0.808 3和0.811 7，如表11中加粗部分所示)。恢复原始标签之后(也就是改变后)，类别cat和类别deer对应的R′值得到显著提升(分别为0.761 4和0.884 1，如表11中加粗部分所示)，对应的类别dog和类别horse的R′值也得到一定的提升(分别为0.821 3和0.896 9，如表11中加粗部分所示)，整体的分类效果评估指标也从0.718 9提高到0.873 0。

Table 10 Confusion matrix 2 before sample label changes表10 改变样本标签前的混淆矩阵2

Table 11 Confusion matrix 2 after sample label changes表11 改变样本标签后的混淆矩阵2

上述实验说明了R′方法对于CIFAR-10数据集的适用性和有效性，进一步说明了R′方法的可拓展性及其应用场景。

此外，结合4.3节和4.4节的实验结果，也就是样本容量发生变化前后评估指标的对比，可以看出该方法对不平衡数据集同样适用。也就是说，它不会因为样本数量的不均衡而影响对分类结果的评价，因为正如3.2节所强调的那样，该方法可以单独对每一个类别进行评估而不仅仅是对整体分类效果进行评估。在不平衡数据集上，即使整体的分类效果较好，对于样本数较少的类别而言，无论它的分类效果如何，它的评价指标都会被单独地呈现出来。这一点正是该方法的一个突出特点。

5 结束语

多分类任务模型准确率评估一直是一个值得讨论的问题，这不仅要涉及到模型选择问题，也对模型训练过程具有很好的指导意义。本文针对多分类任务场景下，尤其是用户关心特定类别分类效果的实际情况，现有的多分类任务准确率评价指标的不足，介绍和引入了用于评估模型分类准确率的R′方法。该方法具有严格的数学理论推导过程，不仅可以评估分类器整体的分类效果，而且还可以给出每一个类别的分类效果，不仅可以用于模型选择，而且对于更好地指导训练过程具有一定的意义。通过与已有评价方法的对比，基于MNIST的手写字符体识别任务和CIFAR-10数据集的多分类任务的实验验证，表明该方法具有很好的鲁棒性和有效性，可以用于多分类任务的分类准确率评估场景。同时值得一提的是，不仅对文中实验验证采用的MNIST手写字符体识别和CIFAR-10数据集分类这2个多分类任务，该方法还可以扩展到任意场景下的多分类任务问题，具有广泛的应用前景。