基于阿当姆斯捷径连接的深度神经网络模型压缩方法*

杜 鹏,李 超,石剑平,姜 麟

(昆明理工大学理学院,云南 昆明 650500)

1 引言

近期机器学习中监督学习的许多突破都是通过深度神经网络的应用实现的,神经网络的深度是获得这些成功最重要的因素之一。在经典图像分类数据集ImageNet上,2012年，Krizhevsky等人[1]使用深度卷积神经网络—AlexNet将1 000分类的正确率提升至84%,AlexNet取得的突破是前所未有的。在接下来的几年里,主流的网络结构突破方向大致是加深网络。Simonyan等人[2]在2014年使用更深层次的网络架构将分类正确率提升至95%。然而简单地增加网络层数并不意味着能提高网络的学习效果,训练更深层次的网络始终是一个巨大的难题。2015年，Srivastava等人[3]提出Highway Networks,借鉴解决循环神经网络RNN(Recurrent Nerual Network)中的问题而被提出的长短期记忆LSTM(Long Short-Term Memory)结构,在深度神经网络中使用门函数来控制信息在层与层之间的流动,形成一种捷径连接方式,解决了梯度信息回流受阻,网络训练困难的问题。之后He等人[4]提出残差网络ResNet(Residual Nerual Network),利用残差学习机制来解决深度神经网络的可训练问题,模型增加一个恒等映射,并通过捷径连接,将残差构件的输出与输入逐个相加。2017年，Lu等人[5]从微分方程数值解的角度出发,提出线性多步结构LM-architecture(Linear Multi-step architecture),以ResNet为基础模型,构造效率更高的深度神经网络模型LM-ResNet。

寻找合适的捷径连接方式指导深度神经网络的结构设计,并辅以对应的网络权重初始化条件以及训练参数设置,可以解决网络的可训练性问题以及模型的效率提升问题。本文将微分方程数值解法—阿当姆斯Adams法思想,迁移到网络结构的设计中，提出一种基于阿当姆斯法的捷径连接(shortcut connection)方式。对类残差学习机制的网络保留残差学习机制，解决梯度消失问题,并将之前相邻残差构件的输入与当前残差构件的输入进行加权求和，使得相邻层之间对于特征的提取更紧密,在网络训练后期梯度值更新幅度较小时,能继续完成对权值的更新，以达到更高的学习精度,使网络变得更有效。特别地,本文以ResNet为基础模型,对于不同的层数,在Cifar10数据集上进行验证,并将基于Adams法的捷径连接方式的ResNet模型Adams-ResNet与源模型ResNet、LM-ResNet进行对比,Adams-ResNet有更好的结果。

2 深度神经网络与微分方程数值解

2.1 深度神经网络与关联的微分方程

多层神经网络的学习与微分动力系统数值解的研究很早就被联系在了一起,将微分动力系统成熟的数值解法迁移到神经网络的学习上是可行的[6]。

类残差网络模型通过组成一个序列来构造复杂的变换将输入转换到隐藏层：

ht+1=ht+f(ht,θt)

(1)

其中,ht∈RD为时刻t的输出，D表示输出的维度,t∈{0,1,…,T},T表示最终时刻，对应网络输出层，θt为时刻t的网络层权重。这些迭代可以视为连续变换的欧拉离散形式[5,7,8]。

当层数足够多步长足够小,在此基础上取极限情况,Chen等人[9]用神经网络对应的常微分方程ODE(Original Differential Equation)来参数化连续动力系统中的隐藏单元：

(2)

从输入层h0出发,可以定义hT的输出。这与微分方程在时刻T的初值求解问题是一致的。

Lu等人[5]从理论上证明了一些类残差学习机制的神经网络与微分方程数值解法之间的联系,例如2016年Larsson等人[10]提出的FractalNet,以及Zhang等人[11]提出的PolyNet，这些深度神经网络都有关联的ODE和与之对应的数值解形式,如表1所示。

Table 1 ODEs and corresponding numerical solutions associated residual-like network 表1 一些类残差网络关联的ODE与数值解方法

2.2 基于Adams法的捷径连接

对于类残差网络关联ODE的初值求解问题,考虑形式如式(1)所示的阿当姆斯法:

(3)

hn+2=hn+1+knfn+(1-kn)fn+1

(4)

其中,kn∈R为对应隐藏层中的可训练参数。特别地当取m=1时,即为微分数值解法中的欧拉法。基于此,本文在类残差网络的残差单元之间构造了Adams法的捷径连接。这种捷径连接方式依赖于源模型的残差单元结构,因此本文更关注比源模型更优的结果。图1所示为采用了不同捷径连接方式的ResNet与Adams-ResNet结构。

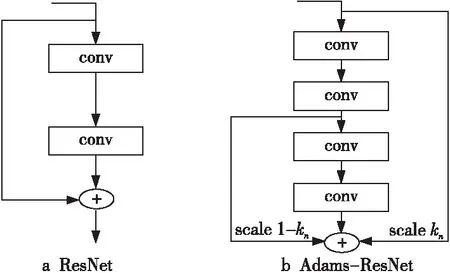
Figure 1 Structures of ResNet and Adams-ResNet using different shortcut connection图1 不同捷径连接方式的ResNet与Adams-ResNet结构

Figure 2 Examples of 10 types of image in Cifar10图2 Cifar10中10类图像示例

3 实验与结果分析

3.1 Cifar10数据集

Cifar10数据集有10个分类，共60 000幅彩色图像,图像像素大小为32×32,每类图像6 000幅,其中5 000幅为训练集,剩余1 000幅为验证集。原数据集中50 000幅训练图像被随机划分为5个批次,每个批次10 000幅,本文实际训练时每重新训练一次都会将50 000幅图像混合再重新随机打乱,避免每次训练时同批次的图像皆为某几类图像，造成网络后期权值更新出现振荡。图2所示为Cifar10中10类图像中随机抽取的10幅图像。

3.2 实验过程

本文直接在50 000幅图像的训练集上进行实验,并使用10 000幅图像的验证集进行评估。同样地,本文关注的是深度神经网络可训练性本身,并不是获取在该数据集上最优的结果。因此,本文使用与He等人[4]相同的简单残差构件单元来验证实验,即使用一个2层的卷积网络构成一个残差构件单元,整个网络结构以一个单层的3×3卷积层开始,紧随着3个不同通道数的残差构件、全局平均池化层和1个全连接层分类层。每个残差构件的残差单元有一个可训练参数kn,并且在模型训练时令其初始值服从[1,1.1]上的均匀分布。其余的权重初始值和批归一化处理BN(Batch Normalization)层初始参数,本文分别采用与文献[12，13]中相同的参数设置,并且同样舍弃了随机失活dropout层,权重衰减率和冲量分别设置为0.000 1与0.9。在Cifar10上训练时,使用随机梯度下降SGD(Stochastic Gradient Descent)优化器训练240次,批次大小为128。为了使网络在前期快速收敛,实验中前40次训练采用0.01的学习率进行热身,41～160次的训练学习率采用0.1,161～180次训练期间学习率降为0.01,余下的每次训练选取衰减率0.01更新学习率直至训练结束。

本文对Cifar10数据集中的图像做了简单的数据增强[14]。在训练时对每幅图像进行零填充,将像素大小扩充到36×36,再随机裁剪出一幅32×32的图像进行随机水平翻转,并利用图像3个通道像素值的均值与方差对其进行归一化处理。这种预处理操作,在每一次训练时都是随机的,避免模型在每次训练时同批次都为相同的输入图像,这样可以增强模型的泛化能力。在验证时,本文使用原始的图像直接进行相同的归一化之后作为网络输入。

如图3和图4所示,模型在学习过程中目标函数损失处于比较平稳的下降过程,合理的冲量和学习率适配网络结构也使得模型在后期微调参数时避免出现振荡,模型随着训练次数的增加学习能力增强,这也一定程度上说明了模型的可训练性。

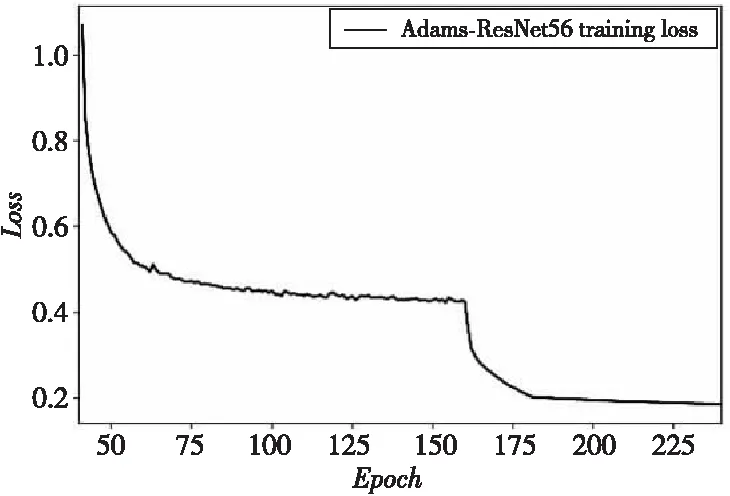
Figure 3 Loss changes of Adams-ResNet56 during training图3 Adams-ResNet56在训练过程中的损失变化

Figure 4 Loss changes of each layer of the network during fine-tuning in later training图4 各层网络在训练后期微调时损失变化

3.3 实验结果

本文比较了20,32,44和56层的Adams- ResNet、ResNet[4]和LM-ResNet[5]在Cifar10上的性能,比较结果如表2所示,其中Params表示参数量。纵向比较,采用微分方程数值解法思想设计的LM-ResNet与Adams-ResNet在每一种层数的网络结构上都是优于源模型的。第2节中建立了类残差学习机制的网络与微分方程的关联,在理论上微分方程数值解法——Adams法在这种类残差学习机制的网络上应是收敛的,本节在后面将通过对网络层中残差单元的kn值与式(5)中Adams法的相容性条件进行比较,进一步分析其收敛性。横向比较LM-ResNet与Adams-ResNet在Cifar10上的性能表现,Adams-ResNet在没有增加参数的前提下达到了更高的识别正确率。尤其在20层与32层的网络结构性能表现上,Adams-ResNet的识别正确率相比ResNet分别提升了1.2%和0.66%,而LM-ResNet的识别正确率相比ResNet仅提升了0.42%和0.33%,基于Adams法的捷径连接方式在网络后期具有更高的学习精度。

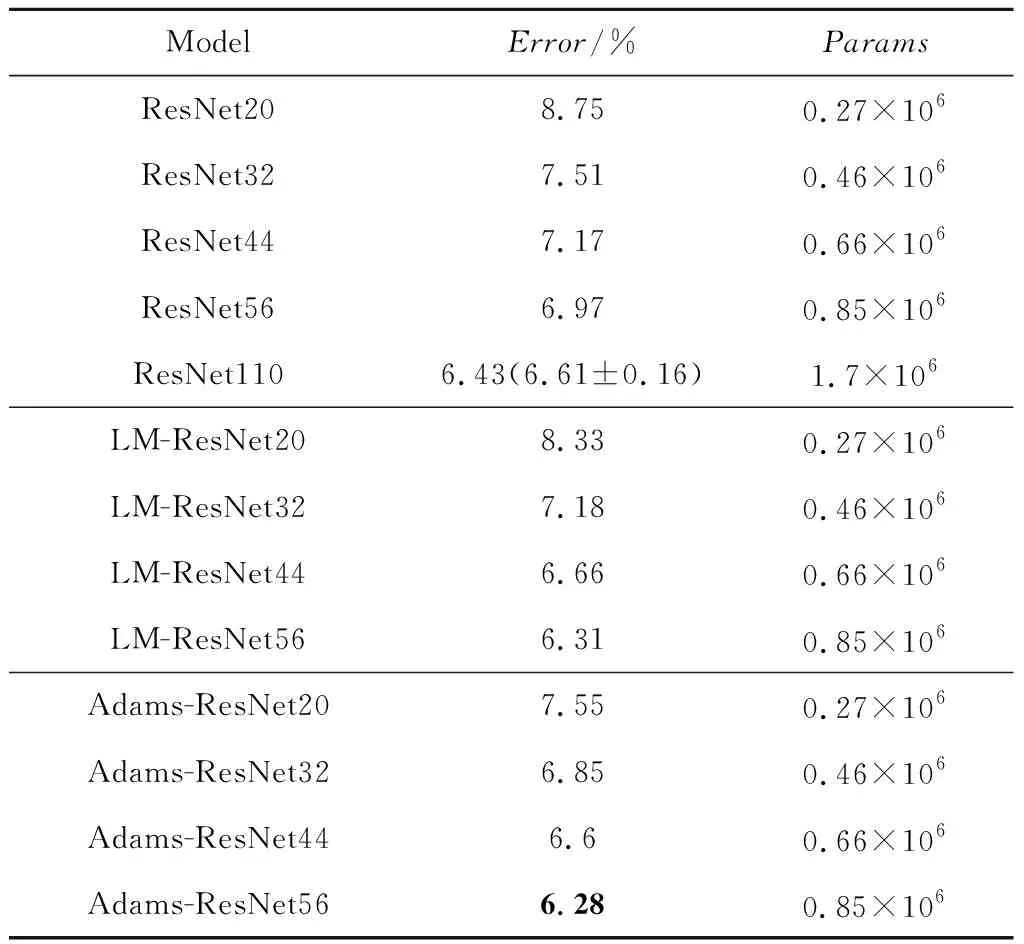
Table 2 Performance comparison of Adams-ResNet with ResNet and LM-ResNet on Cifar10表 2 Adams-ResNet与ResNet、LM-ResNet在Cifar10上的性能对比

图5所示为Adams-ResNet在Cifar10上训练后期识别正确率的变化情况。在第160次训练之后使用较小的学习率对网络的可学习参数进行微调,Adams-ResNet表现出了良好的稳定性,在学习后期取得了优于源网络的学习精度。本文提出的捷径连接方式提升了类残差学习机制神经网络在深度上的可训练性。

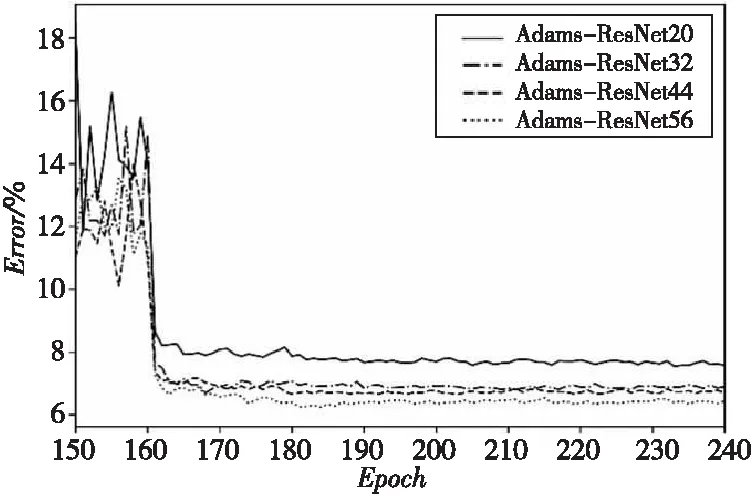
Figure 5 Error changes of in later training of Adams-ResNet on Cifar10 图5 Adams-ResNet在Cifar10上训练后期错误率变化

对于深度神经网络,受到实际应用中算力的影响,模型的复杂度也是一个重要的考虑因素。这就要求在深度神经网络的结构设计中,不仅要追求模型的学习精度,也要考虑模型的大小及其计算量,以得到更有效的深度神经网络模型。表3和图6所示为基于Adams法的捷径连接方式应用到ResNet上时,模型的性能表现与参数量的关系，表3中Ratio-to-Adams-ResNet表示在基本相同的正确率下改进前后的模型参数量的比值。Adams-ResNet在Cifar10数据集上在达到更高的识别正确率的前提下,参数量更少。取得最高识别正确率的Adams-ResNet56仅使用了源模型一半的参数量,将模型的深度由110层降至56层，且未降低模型的学习精度,有效地压缩了模型,避免模型出现参数冗余。基于Adams法的捷径连接方式能使类残差学习机制深度神经网络变得更有效。

Table 3 Parameters of Adams-ResNetand its performance on Cifar10表3 Adams-ResNet参数量及在Cifar10上的性能表现

Figure 6 Performance of models on Cifar10图6 模型在Cifar10上性能表现

图7所示为在Adams-ResNet中隐藏层中残差单元的可训练参数kn值,横坐标为类残差单元的索引值。从折线的变化趋势来看,不同层数的Adams-ResNet的隐藏层中kn的总体变化情况是基本一致的。这是由于示例网络在对数据集进行从基础纹理特征到抽象特征提取的过程中,类似特征出现在了各网络不同的阶段,而Adams法在学习过程中对这些特征比较敏感,这种敏感并不会随着网络层数的减少而丢失,这造成了Adams法应用在层数较少的深度神经网络上时,有效性提高得更明显；从kn的取值来看,除去临近输出层的少数隐藏层,绝大多数的值都分布在[-1,0]。在文献[15]中证明了二步的显式阿当姆斯法与式(2)中的微分方程是相容的,则满足：

(5)

此时,β0=-0.5.这与Adams-ResNet中的取值区间是一致的。这同样也是虽然本文仅在ResNet上验证,但认为基于Adams法的捷径连接方式推广到其它类残差网络上仍能有效地压缩模型,抑制深度神经网络在训练后期出现的振荡现象,提升网络的可训练性的原因。

4 结束语

本文针对深度神经网络现在广泛存在并仍待解决的可训练性问题,寻找一种合适的捷径连接方式来设计类残差学习机制神经网络,从微分方程数值解法—Adams法本身具有的性质出发,构造残差单元之间的捷径连接方式,使得源模型在训练后期具备更强的学习能力的同时,压缩模型的规模,这对于今后设计更有效的深度神经网络有一定的启发性。本文以经典的ResNet为例设计了Adams-ResNet,寻找了与所提基于阿当姆斯捷径连接方式适配的实验参数设置,在Cifar10上表现出了比源模型更优的性能。然而该种捷径连接方式依赖于源模型的结构来构造更有效的深度神经网络,更关注对源模型大小的压缩,提高模型的效率,如果想要获得在各类图像识别任务上最先进的结果,仍需寻找合适的源模型结构,这同样也是如今深度神经网络结构设计的一大难题。