垫板阻尼对地铁线路轨道垂向特性的影响研究

黄乾兴

（柳州铁道职业技术学院，广西柳州，545616）

0 引言

地铁线路轨下胶垫作为轨道结构中的重要减振部件，合理的胶垫参数不仅能保证线路的弹性，还可以改善轮轨间的动态作用，从而延长轨道的寿命[1]。因此研究轨下垫板阻尼对地铁线路的影响十分必要。

袁玄成等人通过细化传统车辆-轨道垂向耦合动力学模型，建立了考虑轨下垫板初始压缩量的动力学模型，分析了钢轨扣件弹条扣压力对轮轨系统垂向动力学响应的影响。研究表明：失效扣件个数对轮轨间的垂向力、钢轨的垂向位移的变化影响很小[1]。张攀等人分析了垫板参数随时间变化的特性，结果表明:随着垫板使用时间的增长，轨下橡胶垫板的刚度将逐渐变大[2]。李晶通过建立车辆-轨道-桥梁动力学模型，研究了轨下垫板滑出对轨道线路的动力学性能影响，得出垫板的滑出量不宜大于120mm的结论[3]。张树峰采用ANSYS有限元分析软件，分析了垫板参数对弹条振动特性的影响，研究结果显示波磨深度的增加、轨下胶垫刚度的减小会增大弹条的垂向振动，加剧弹条的疲劳损伤[4]。唐剑等人研究了轨下垫板泡在水中时无砟轨道轨下胶垫刚度的时变特性及其对轮轨系统的影响，得出垫板刚度的变化钢轨位移影响较大[5]。

由上可知，对垫板的研究主要集中在高速铁路轨下垫板对车体或轨道系统的影响，对地铁线路轨下垫板的研究较少，因此研究地铁线路轨下垫板对车辆-轨道系统的影响已经十分紧迫。本文依据车辆－轨道耦合动力学理论，建立了地铁－轨道垂向耦合动力学模型，通过仿真计算，深入探究了轨下垫板刚度对系统的影响。

1 理论依据

1.1 车辆－轨道垂向耦合动力学模型

车辆－轨道耦合动力学是将车辆和轨道通过轮轨耦合作用构成一个整体系统。因为车辆运行时，车体的振动会向下传递，同时轨道系统的振动也会向上传递，两者互相影响[6,7]。本文所建地铁－轨道垂向耦合动力学模型如图1所示。

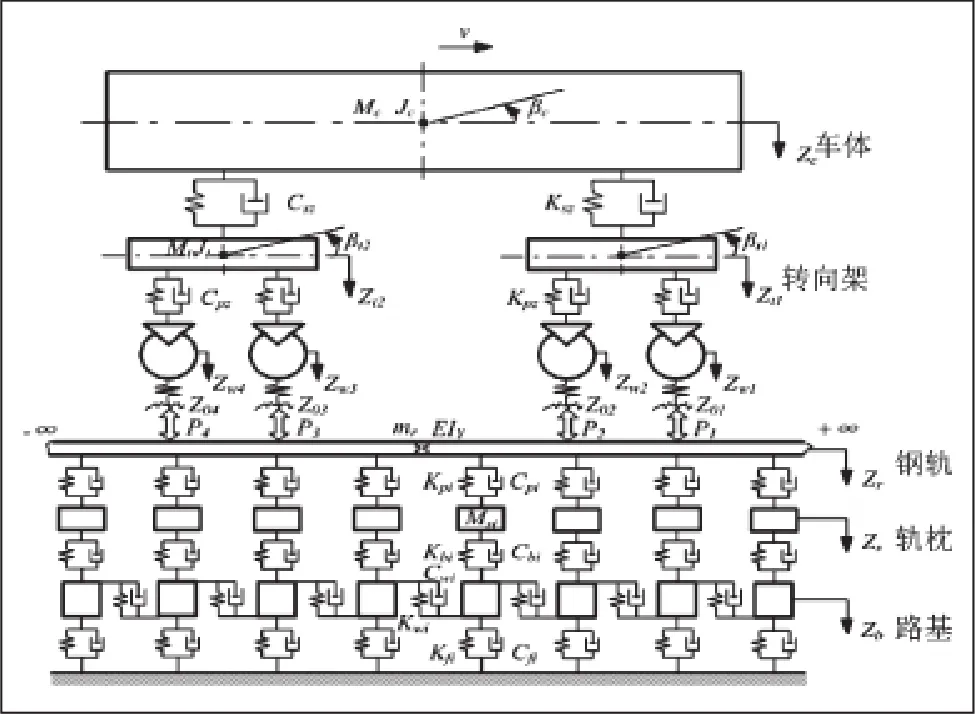
图1 地铁—轨道垂向耦合动力学模型

利用该耦合模型可以计算车辆运行时的运行特性和轨道线路的垂向动态响应。本文以地铁A型车为研究对象，主要参数如表1所示。

表1 地铁车辆-轨道系统主要参数

1.2 新型快速显式积分法

车辆－轨道垂向耦合动力学方程可写成统一形式

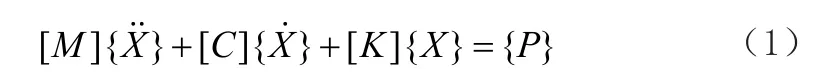
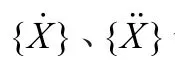
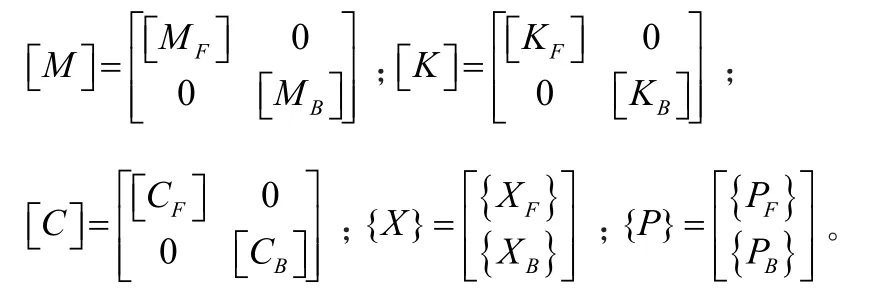
新型快速显式积分法[6]的基本原理是：根据前两步计算得到的速度、位移和加速度量来预测下一步的速度量和位移，再根据运动方程解出下一步的加速度量，如此循环递推。其格式如下所示：

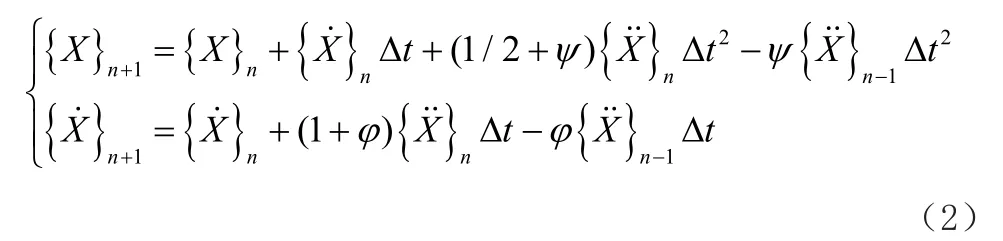
式中，积分步长Δt；积分参数ψ=φ=0.5；n为计算的积分步数。

再将式（2）代入到式（1）中，并假设阻尼矩阵[C]和刚度矩阵[K]参数保持不变，可求得t=(n+1)Δt时刻的系统运动振动微分方程

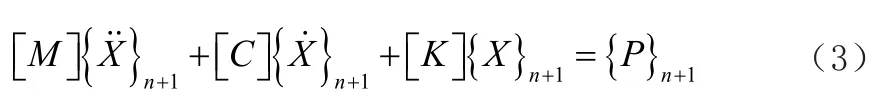
通过转化可得系统加速度

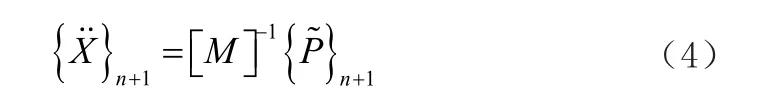
其中

假设初始时刻车辆和轨道系统的各部分位移和速度都是0

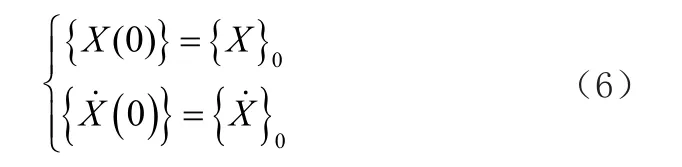
那么

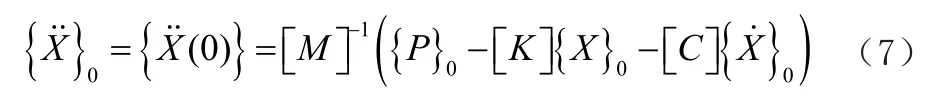
根据式（1）和（4）解出各积分步长下的位移、速度和加速度的离散值。

2 轨下垫板刚度对轮轨动力学性能影响

2.1 轮轨垂向力响应

由图2可知，垫板阻尼从30kN·s/m逐渐增大到150kN·s/m时，轮轨垂向力由63.78kN逐渐减小到58.7kN。因此，地铁垫板阻尼在30kN·s/m～150kN·s/m范围内，随着垫板阻尼的增大，可以减小轮轨间垂向力，从而降低对线路的破坏。

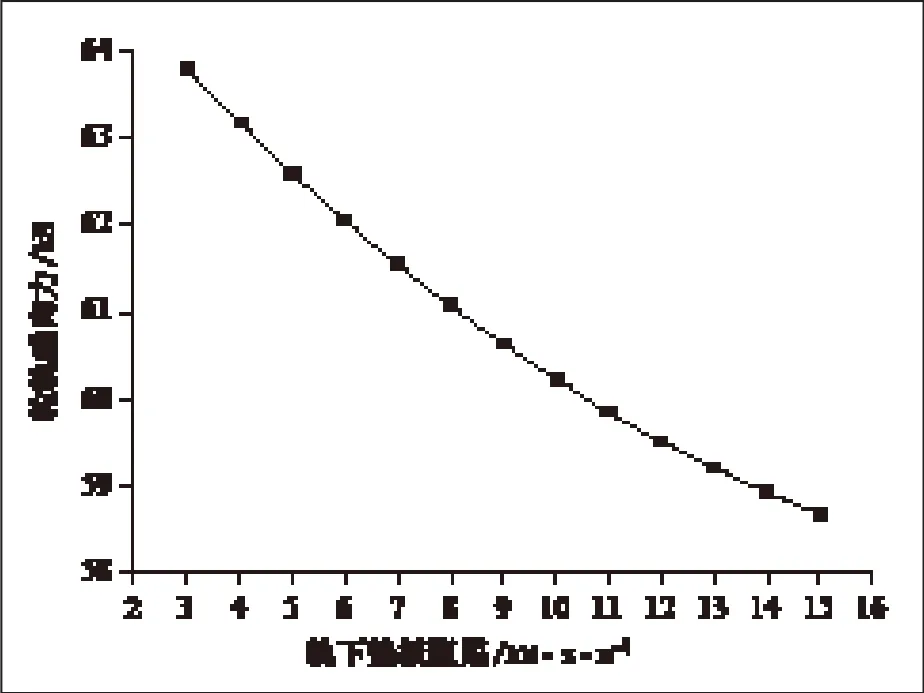
图2 垫板阻尼对轮轨力的影响

2.2 轨道板、道床垂向位移响应

从图3、4可知，随着垫板阻尼的增大，轨道板和道床的垂向位移逐渐减小，由此可知，增大垫板阻尼，可以减小轨道板和道床的下沉量，减缓轨道发生形变，减少轨道维护费用。

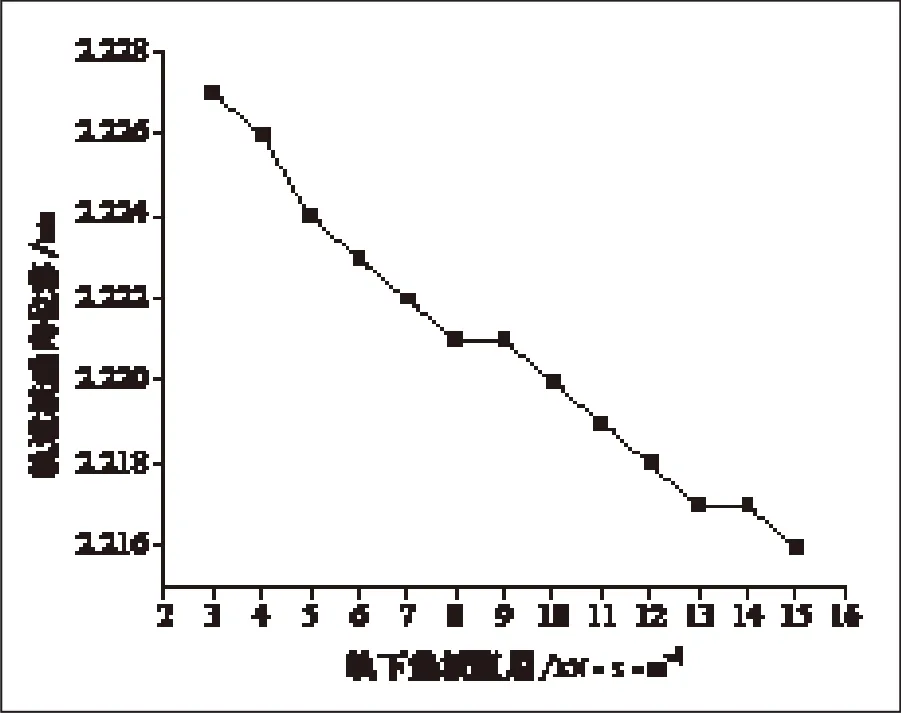
图3 垫板刚度对轨道板垂向位移的影响

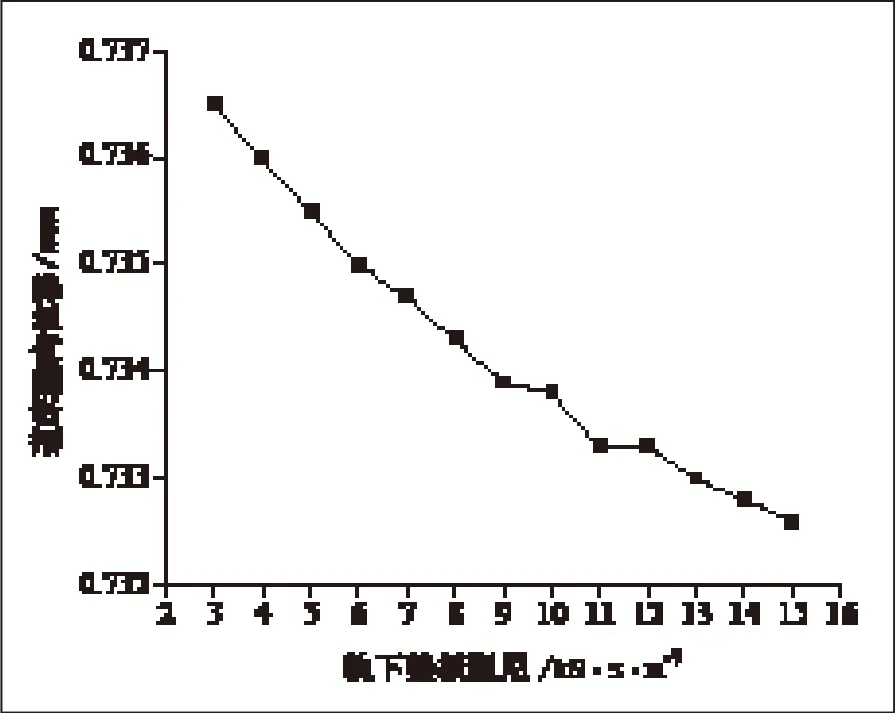
图4 垫板刚度对道床垂向位移的影响

2.3 轨道板和道床垂向加速度响应

由图5、6可知，垫板阻尼从30kN·s/m逐渐增大到150kN·s/m时，轨道板垂向加速度由17.17m·s-2增大到77.54m·s-2，增大了约352%；道床垂向加速度由0.52m·s-2增大到1.95m·s-2，增大了约275%，由此可知，垫板阻尼对轨道板和道床的垂向振动的影响十分明显。因此，选用合理阻尼的轨下垫板对降低轨道振动，延长轨道的使用寿命有十分重要的作用。

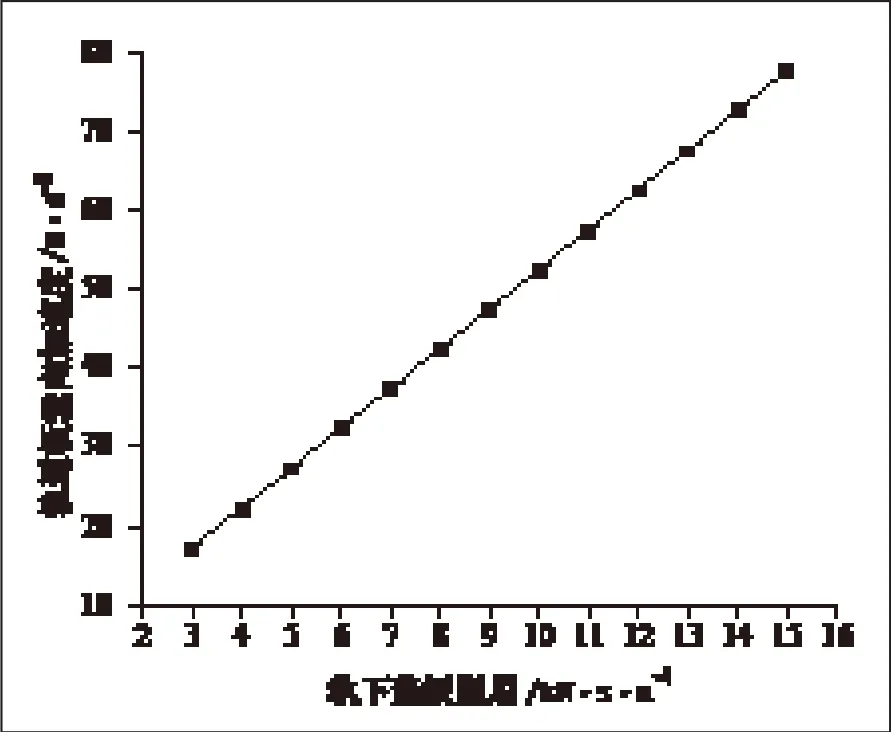
图5 垫板刚度对轨道板垂向加速度的影响

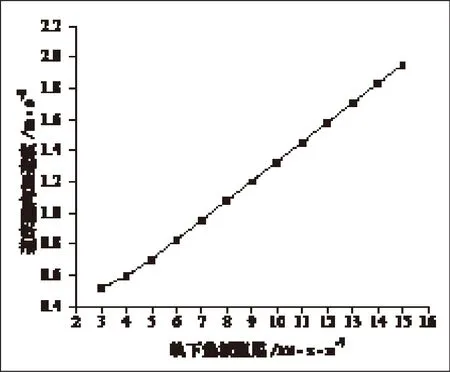
图6 垫板刚度对道床垂向加速度的影响

3 结论

1.当轨下垫板阻尼从30kN·s/m逐渐增大到150kN·s/m时，轮轨垂向力、轨道板和道床的垂向位移均逐渐减小；轨道板垂向加速度，增大了约352%，道床垂向加速度增大了约275%。因此，低阻尼的轨下垫板有利于降低轨道板和道床的振动，同时又会增大轮轨垂向力、轨道板和道床的垂向位移，所以选用垫板时其阻尼要在合理范围内才能有效提高轨道的平稳性。