具有精确幅值积分特性的正交信号发生器

孙于，李雪，耿嘉一，吴尚

(1.河北工业大学 省部共建电工装备可靠性与智能化国家重点实验室，天津 300132； 2.中国电工技术学会，北京 100055)

0 引 言

正交信号发生器(quadrature-signal-generator, QSG)可以产生一组较为精准的正交信号，在电网同步[1]、单向功率的瞬时计算[2]以及三相系统的对称分量提取等场合有着较大的应用潜力以及产业价值[3-5]。其中，运用二阶广义积分器的正交信号发生器(second-order-generalized-integrator based quadrature-signal-generator, SOGI-QSG)来提取正交分量的方法应用最为广泛，其结构简单、性能优越[6-11]，在虚拟磁链积分[10,12]、机电振荡估计[13]、无传感器电机控制[14]等方面发挥着重要的作用。然而，文献[4]和文献[15]表明，SOGI-QSG在参数设计以及提取效果方面存在一定的不足与局限性，可以归纳为以下两个方面。

一方面，由于SOGI-QSG可以表述为2个具有二阶特性的传递函数，因此其动态性能的分析和设计可以参考典型二阶系统的设计思路(second-order-system,SOS)[8,15]。SOGI-QSG的调节时间通常被设定为实际响应与稳态输出的误差达到并保持在最终值的2%以内所需要的时间(在某些情况下，使用1%或5%)[16]。该设计方法规则简洁且易于实现，因此多数研究学者对于SOGI-QSG的参数设计均采用这一规则。然而，与标准SOS不同的是，SOGI-QSG的有源输入部分并非直流信号而是正弦信号，其同时具有幅值、相位和频率3个特征量。因此，对于SOGI-QSG而言，其调节时间并不能准确反映系统的实际状态，导致调节时间失去了实际意义。

另一方面，广义积分器(generalized-integrator,GI)作为SOGI-QSG的核心[6]，对于正弦信号具有幅值积分特性[17]，即当二阶广义积分器(second-order-generalized-integrator,SOGI)的谐振频率与输入信号频率相同时，其工作特性与一阶系统(first-order-system,FOS)中纯积分器的直流积分特性一致，因此可以从FOS的角度理解SOGI-QSG。然而，文献[17]表明，GI会受到输入信号初始相位的影响，使其积分特性不稳定。当输入信号的初始相位为0时，其积分效果与FOS一致，可以实现交流信号的精确跟随；但当其初始相位不为0时，GI将不再是一个精准的幅值积分器(magnitude-integrator,MI)，因此SOGI-QSG的准确性也将严重下降。文献[18]提出了降阶广义积分器(reduced-order generalized integrator,ROGI)的概念，将GI分解为正序MI以及负序MI，并分别对两个MI进行设计，从而一定程度上消除了初始相位的影响。然而，由于其复杂的矢量表达式，使得ROGI在单相系统中不易实现。

为了能够获取精准的正交信号，并且能参考FOS的动态过程来设计简单且易于实现的应用要求，本文在SOGI-QSG的基础上提出了一种基于精确幅值积分器的正交信号发生器(accurate-magnitude-integrator based quadrature-signal-generator,AMI-QSG)。与SOGI-QSG相比，AMI-QSG具有更清晰的结构和概念，同时可以实现直流抑制以及谐波提取。

本文首先从FOS的角度对SOGI-QSG的原理进行阐述，并指出其在参数设计以及实际应用中存在的问题。在此基础上，提出了可以精确获取正交信号的AMI-QSG。其次，为了更好的应对实际应用中的问题，进一步对其结构进行改进，在得到正交信号的同时，实现直流分量的抑制以及谐波分量的提取。最后，实验验证所提出AMI-QSG的优良性能。

1 SOGI-QSG的原理及问题分析

1.1 FOS角度分析SOGI-QSG

图1为标准FOS的结构框图，由于纯积分器对直流信号具有无穷大的增益，因此其输出可以跟随直流输入，使其稳态误差为0。FOS的闭环特性与低通滤波器相同，传递函数为

图1 标准一阶系统(FOS)框图Fig.1 Block diagram of the standard first-order system (FOS)

F(s)=kdc/(s+kdc)。

(1)

其中kdc为一阶系统的增益。

为了更好的实现对交流信号的跟随，可以用SOGI取代FOS中的纯积分部分，从而得到SOGI-QSG结构[19]，如图2所示。GI是SOGI-QSG的核心构件，其传递函数[8]为

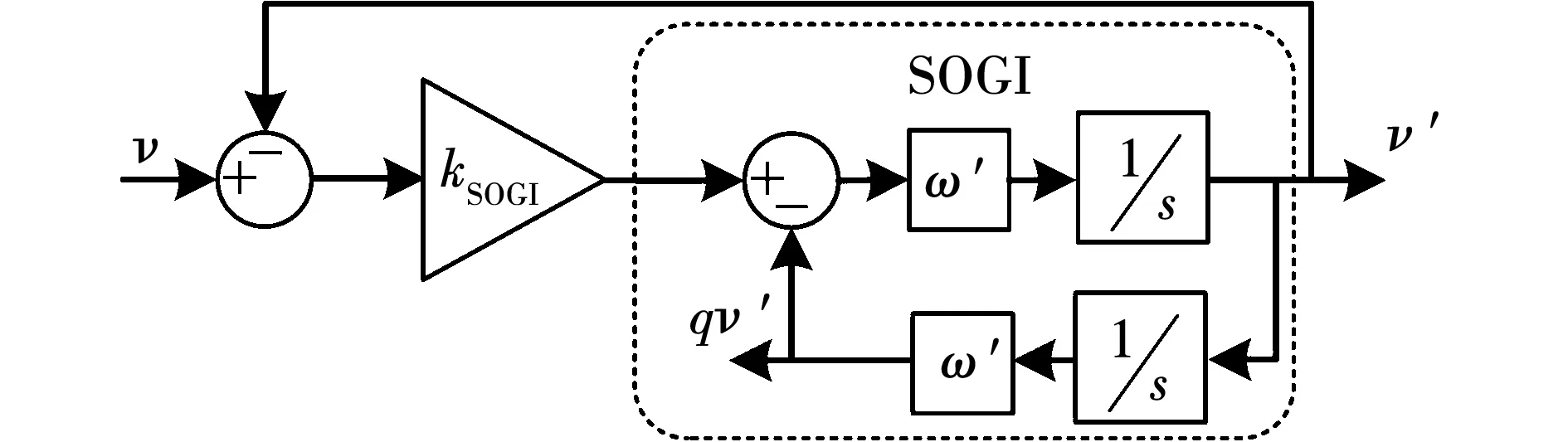
图2 基于二次广义积分器的正交信号发生器(SOGI-QSG)的结构框图Fig.2 Block diagram of the second-order generalized integrator based quadrature signal generator (SOGI-QSG)

(2)

该结构的输出信号v′以及qv′分别为输入正弦信号的同相信号和正交信号，两个正交分量的传递函数分别为：

(3)

(4)

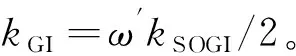
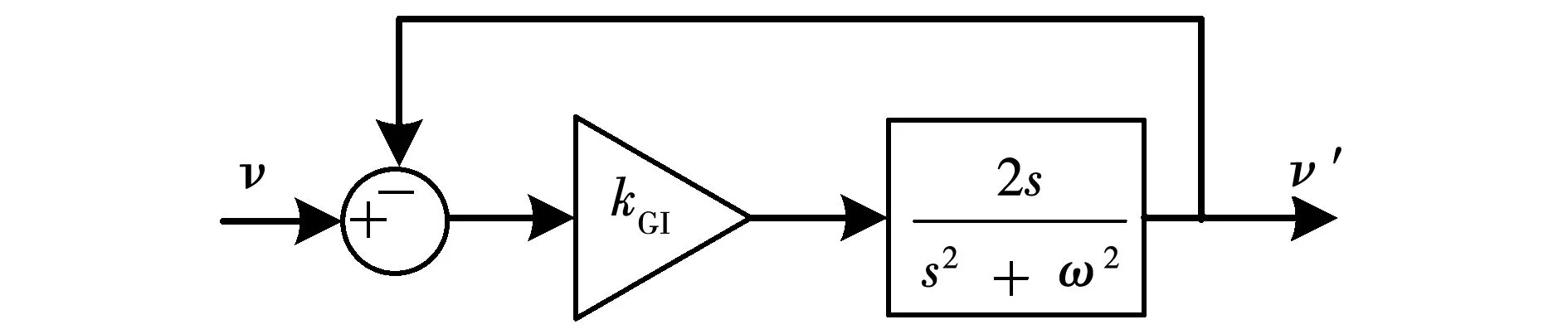
图3 GI-QSG的结构框图Fig.3 Block diagram of the GI-QSG

为了观察GI-QSG和FOS的响应过程，图4和图5分别给出了FOS对阶跃信号的响应以及GI-QSG对正弦信号的幅值阶跃响应。阶跃响应的表达式为

v′(t)=A(1-e-tkdc),t≥0。

(5)

其中包括与输入信号大小相等的稳态项以及由kdc决定时间常数的指数衰减项。在FOS中，将t=4T=4/kdc时刻定义为该系统的稳态时间ts，则由式(4)可以计算出，在4T时刻系统的误差为1.83%，如图4所示。在GI-QSG中，输入信号为一定频率的正弦信号，从图5的仿真对比结果可以看出，GI-QSG的幅值响应与FOS的阶跃响应并不能实现理想的同步。因此，为了能够更好的参考FOS的动态响应的设计准则来设计GI-QSG的参数，还需对GI-QSG的动态响应存在的问题做进一步分析。

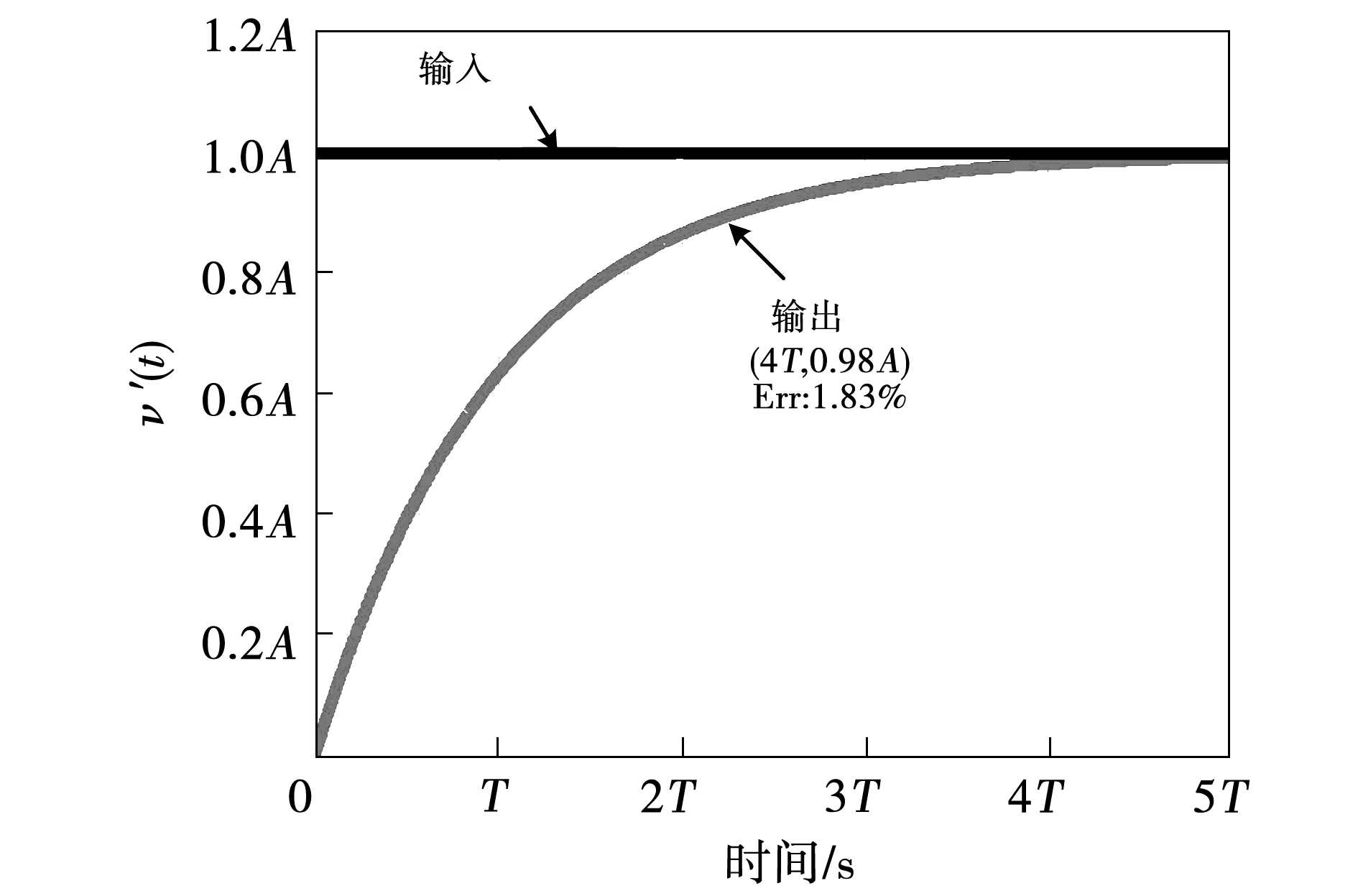
图4 FOS阶跃响应Fig.4 Step response of the FOS

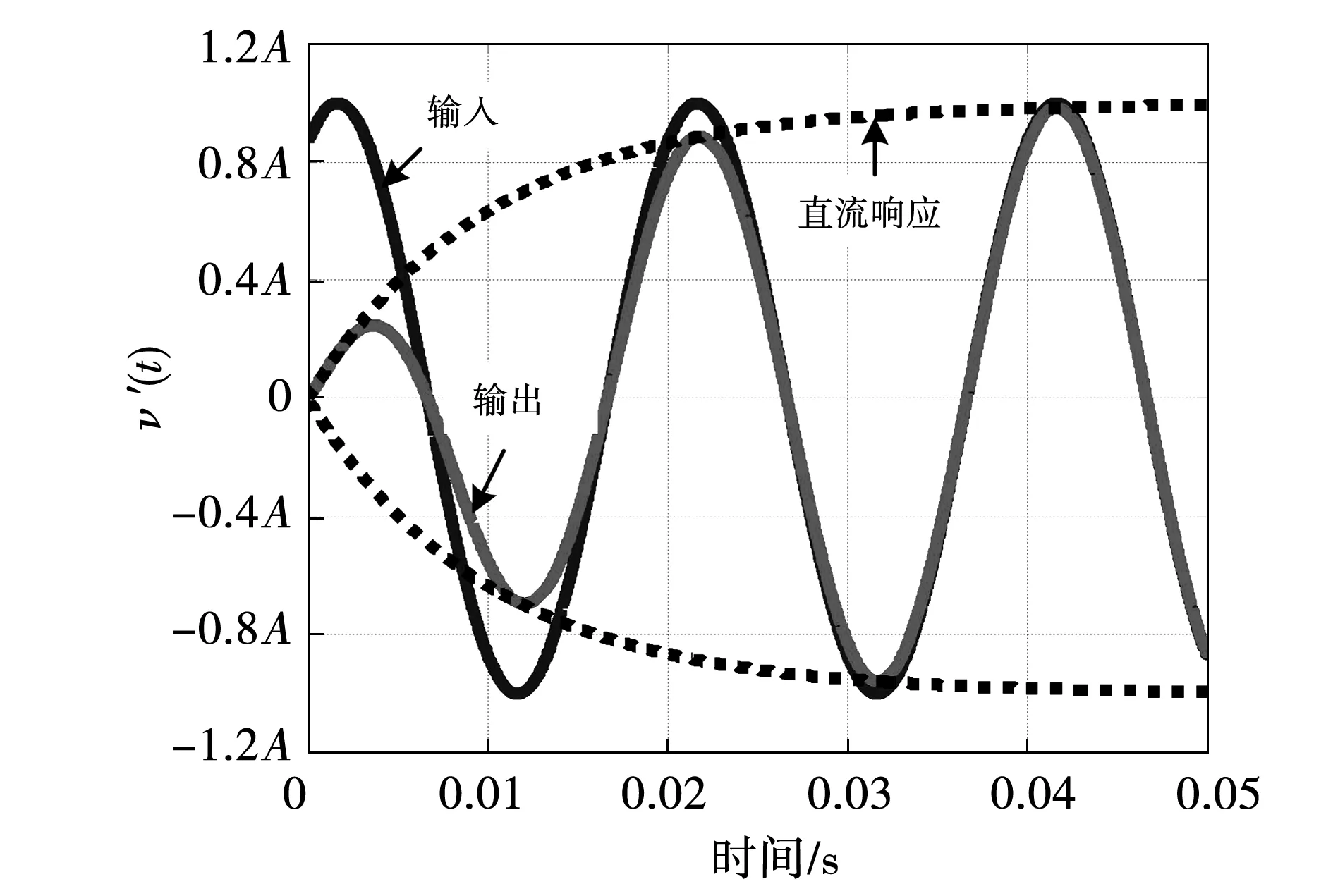
图5 GI-QSG正弦信号的幅值阶跃响应Fig.5 Magnitude step response of the GI-QSG for sinusoidal signal

1.2 GI-QSG的问题分析

如前所述，FOS中的纯积分环节在零频点处具有无穷大的增益，因此可以实现对直流信号的无差跟踪。然而，与纯积分器不同的是，GI是由两个较为复杂的积分器组合而成，即

(6)

由式(6)可知，GI在正频域和负频域内都存在无限增益的频率点，其理想情况下时域响应为

v′(t)=A(1-e-tkac)sin(ωt+φ)。

(7)

其中kac为理想情况下的系统增益。

如果反馈系统是由与之相对应的复杂积分器构成，则式(7)中跟踪特性将与FOS的跟踪特性一致。当GI-QSG输入单一频率的正弦信号时，式(6)中只有一个积分器对该信号进行跟踪，而另一个积分器的存在干扰了系统的跟踪过程，导致系统的动态响应与FOS出现较大的差异。并且，当系统需要快速响应时，GI-QSG的幅值响应与FOS的差异将更为显著。为了更好的解释这个问题，需要推导出GI-QSG对正弦输入信号v(t)=Asin(ωt+φ)的时域响应，并与式(7)中的理想响应进行比较。

首先，正弦输入信号v(t)=Asin(ωt+φ)的拉普拉斯变换为

(8)

GI-QSG输出的拉普拉斯变换可以通过式(8)与式(3)相乘得到(v′(s)=v(s)D(s))。当调节D(s)中的ω′使得ω′=ω时，时域响应可以通过v′(s)的拉普拉斯逆变换得到，即

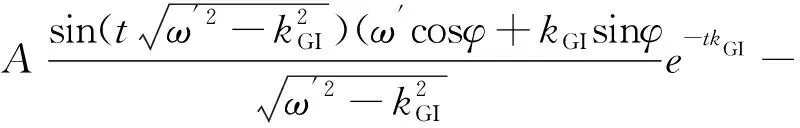
(9)

与式(7)中的理想响应相比，式(9)中有相同的稳态项，但有不同的指数衰减项。为了验证在快速动态响应情况下，FOS的参数设计规则对于GI-QSG的有效性，将稳定时间设定为0.005 s (kGI=800)，随后对GI-QSG的正弦信号响应进行仿真，并与理想M-FOS进行对比，结果如图6所示。由图可知，GI-QSG在0.005 s时产生了15.46%的跟踪误差，与理想M-FOS相比跟踪误差明显。因此，对于具有快速动态响应的GI-QSG系统，基于一阶系统的设计规则不再适用。

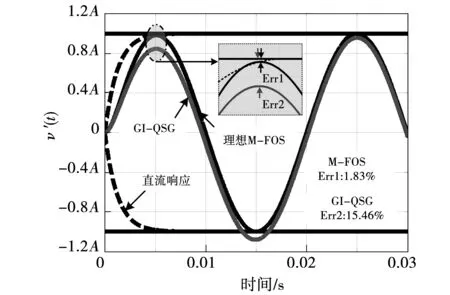
图6 GI-QSG与理想M-FOS的阶跃响应的比较Fig.6 Magnitude-step-response comparison of the GI-QSG and the ideal M-FOS

2 基于精确幅值积分器的正交信号发生器(AMI-QSG)

由式(9)可以看出，GI-QSG的瞬态响应是高度非线性的，这使得其参数设计非常困难。解决这一问题的方案为在闭环系统中应用一个与FOS有相同幅值响应的正弦积分器，但是该系统需要输入复杂的交流信号，这在单相系统中并不容易实现。为了适应复杂的交流输入信号，在本节中运用反向推导的思想提出了一种新型积分器的设计方案，该方案与 GI-QSG相比更接近FOS响应。

2.1 精确幅值积分器(accurate magnitude integrator,AMI)的推导

首先,对正弦输入信号v(t)=Asin(ωt+φ)进行拉普拉斯变换，其结果为

(10)

理想的幅值响应由式(7)给出，其拉普拉斯变换为

(11)

利用上述输入信号和输出信号的传递函数，可以推导出跟踪系统的闭环传递函数，进而计算出开环传递函数为

(12)

式(12)为理想正弦积分器的传递函数，其对应跟踪系统的幅值响应与FOS相同。然而，可以注意到传递函数O(s)与输入信号的初始相位有关，但是在实际中初始相位很难获得，实现起来较为复杂，因此假设相角为0，式(12)可以简化为

(13)

由此，便得到AMI的结构表达式(13)。与GI类似，AMI只与信号频率和时间常数有关，因此相较于式(12)更容易实现。由于式(13)仅为一个特例，因此有必要对该积分器在一般情况下的有效性进行验证。为此，首先给出由式(13)建立的闭环系统的传递函数为

(14)

其次将v(t)=Asin(ωt+φ)作为系统的输入信号，可以导出其时域响应为

v′(t)=Asin(ωt+φ)-Asin(ωt+φ)e-kact+

(15)

与式(9)相比，式(15)更接近于理想M-FOS的时域响应。由式(15)可以看出，仅在输入信号初始相位为0时，AMI的时域响应与式(7)中理想M-FOS相同；当输入信号初始相位不为0时，两种积分器的响应结果仍然存在差异。为了测试AMI对不同初始相位正弦信号的性能，给出了4个不同初始相位的仿真结果，如图7所示。从图7(a)中可以看出，当初始相位为0时，AMI跟随一阶系统的响应，响应速度快于GI-QSG；当初始相位不为0时，如图7(b)、(c)、(d)所示，AMI的响应速度还要快于FOS。这些结果说明即使在不忽略初始相位的一般情况下，AMI仍然具有较强的优越性。

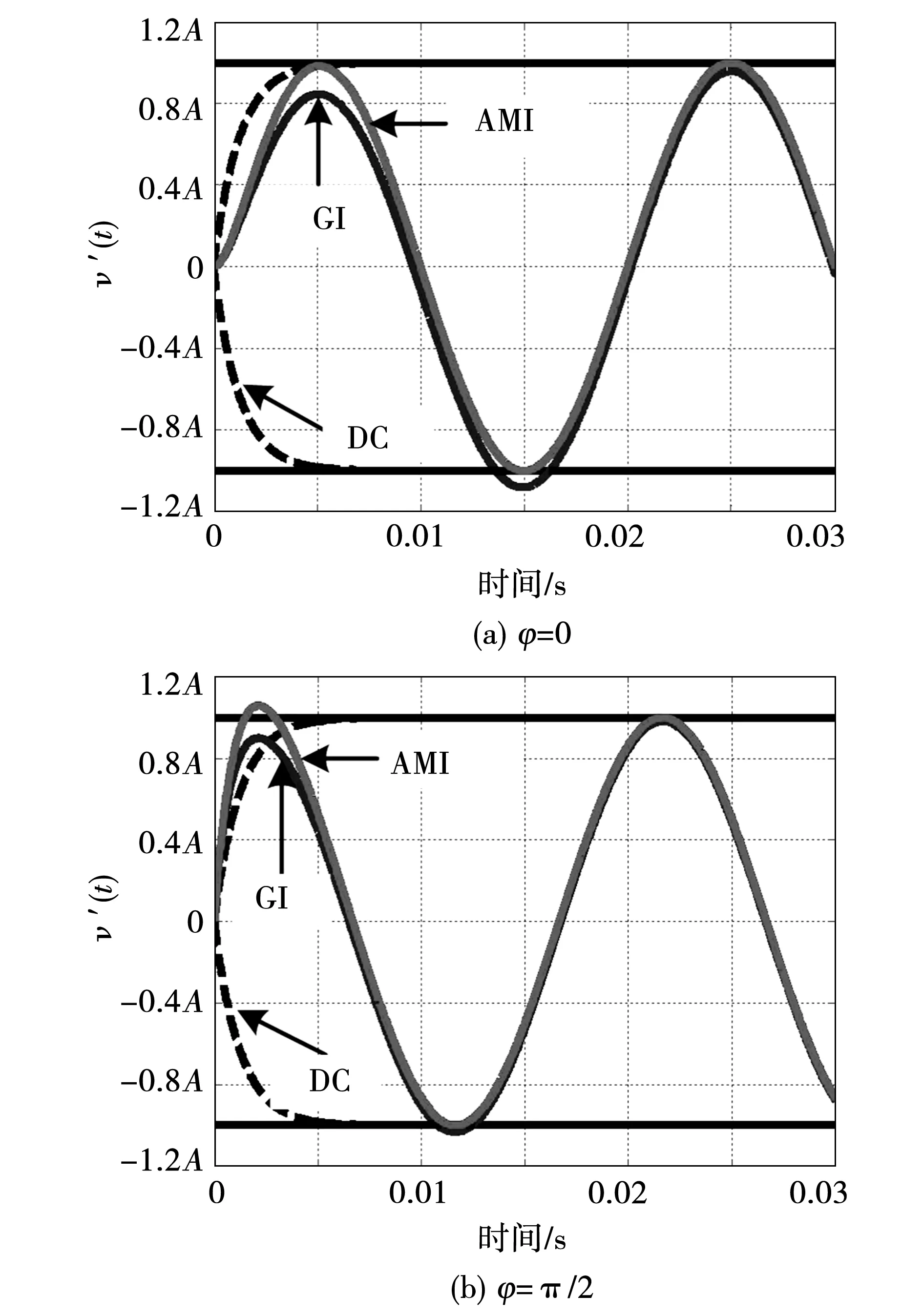
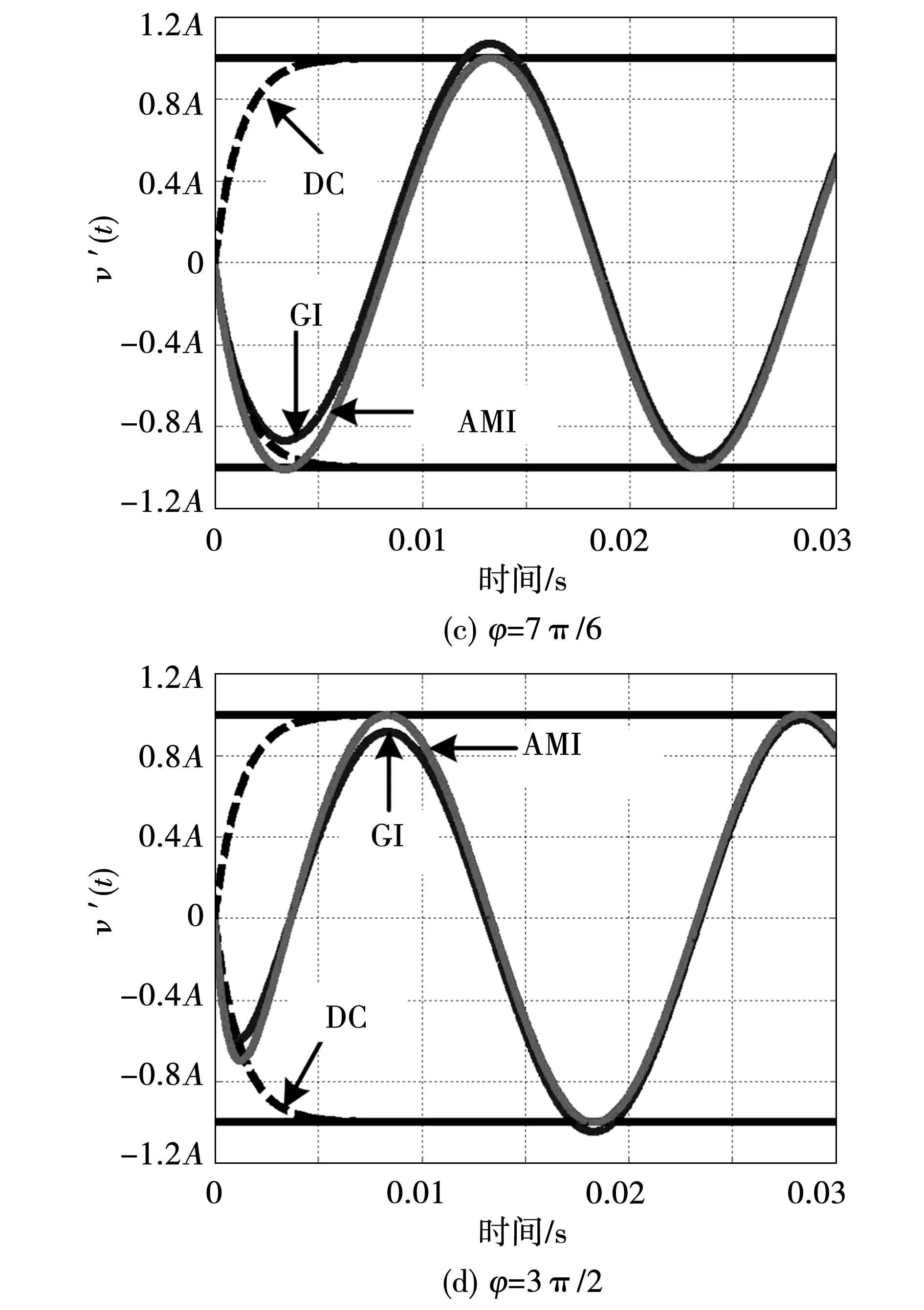
图7 GI-QSG和基于AMI的M-FOS在不同初始相位情况下，正弦输入信号的阶跃响应比较Fig.7 Magnitude-step-response comparison of the GI-QSG and the AMI based M-FOS for the sinusoidal input signal with different initial phases

2.2 基于AMI的QSG的结构实现

传递函数(13)可以改写为

(16)

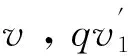
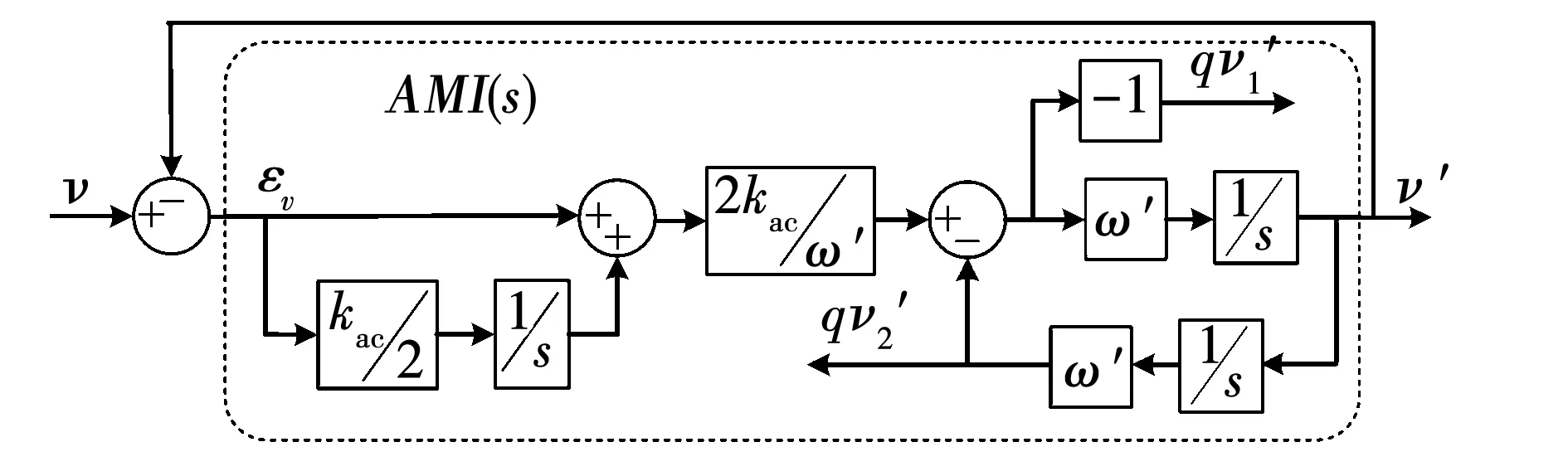
图8 基于AMI的QSG(AMI-QSG)的结构实现Fig.8 Structure realization of the AMI based QSG (AMI-QSG)

(17)

(18)

(19)

(20)

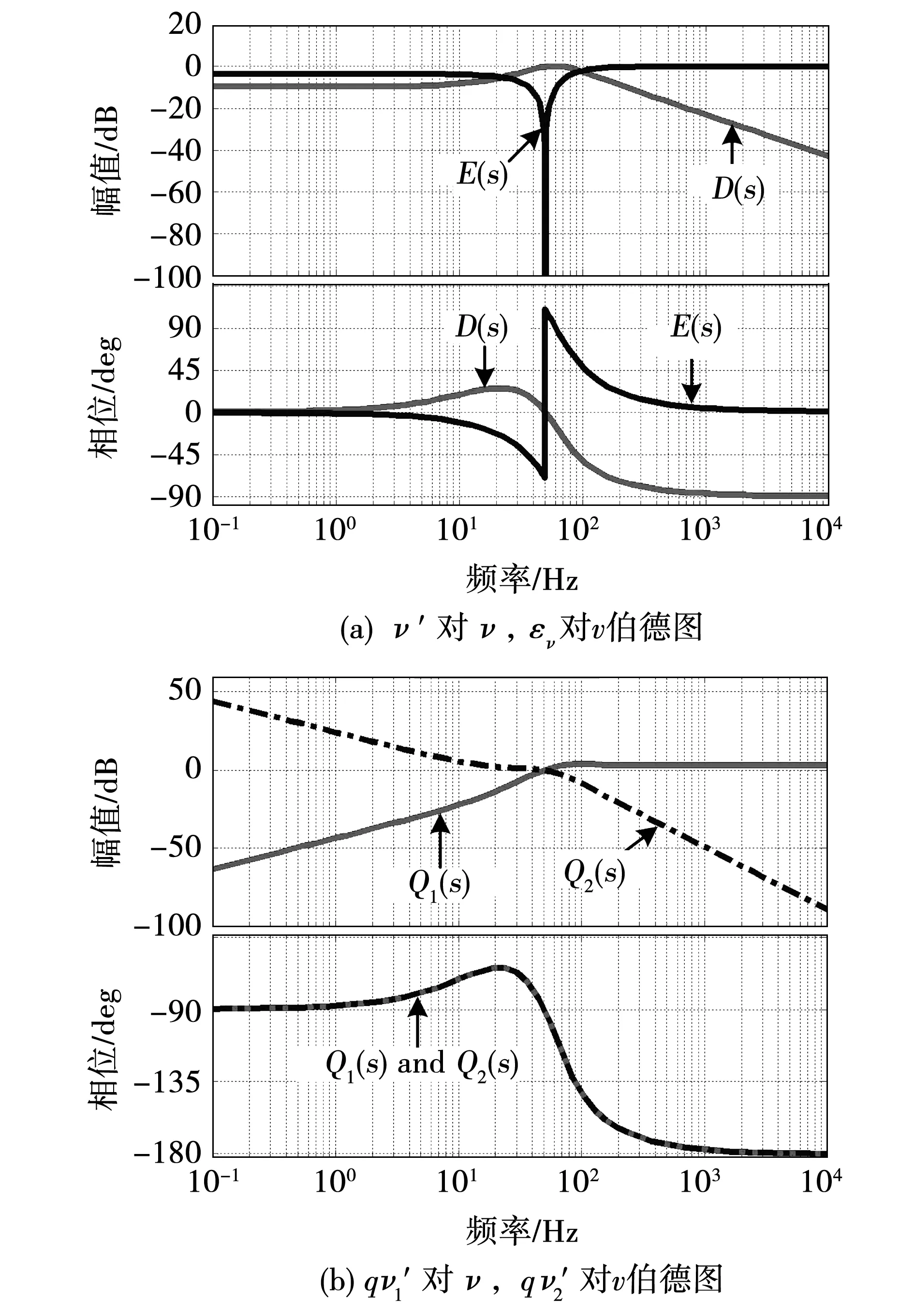
图9 AMI-QSG的伯德图Fig.9 Bode diagrams of AMI-QSG

AMI-QSG基于一阶系统的动态响应特性，运用逆推的思想，实现了交流信号的动态追踪，为了保证图8的结构更好的应对实际应用中的问题，以下对其结构进行了改进，并在实验验证中验证了其优越性。

2.3 AMI-QSG的结构改进

考虑到FOS可以实现直流提取，因此将其与AMI-QSG结合来实现直流抑制，从而得到FOS和M-FOS的组合结构，如图10所示，其中v′与v，εv与v的传递函数分别为：

(21)

(22)

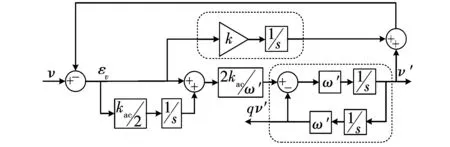
图10 具有直流抑制的AMI-QSG改进结构Fig.10 Improved AMI-QSG structure with dc rejection(AMI-QSG)

(23)

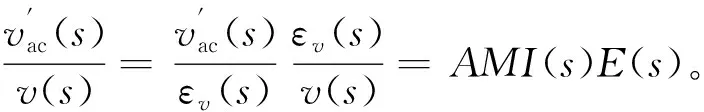
(24)

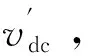
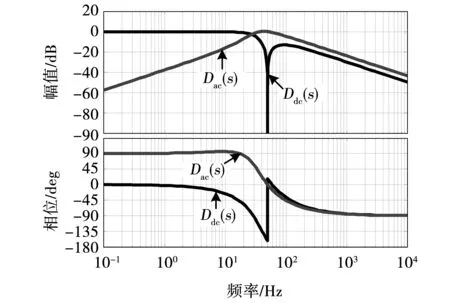
图11 改进版AMI-QSG的伯德图Fig.11 Bode diagrams of improved AMI-QSG

除了直流问题，另一个实际问题是低次谐波的存在会对基波分量的提取产生影响。尽管Dac(s)自身具有滤波特性，对高次谐波分量有较强的抑制能力，但是接近基频的低次谐波仍然会使提取的基频分量产生较大的畸变。此外，AMI-QSG的正交输出具有高通滤波特性，使其对低次谐波更加敏感。为了解决这些问题，可以通过改变固有频率(ω′)的取值，得到与低次谐波分量相对应的AMI-QSG结构，随后将其并联得到MAMI-QSG，如图12所示。该结构可以实现对相应谐波分量的提取，其有效性将在下一节中得到验证。

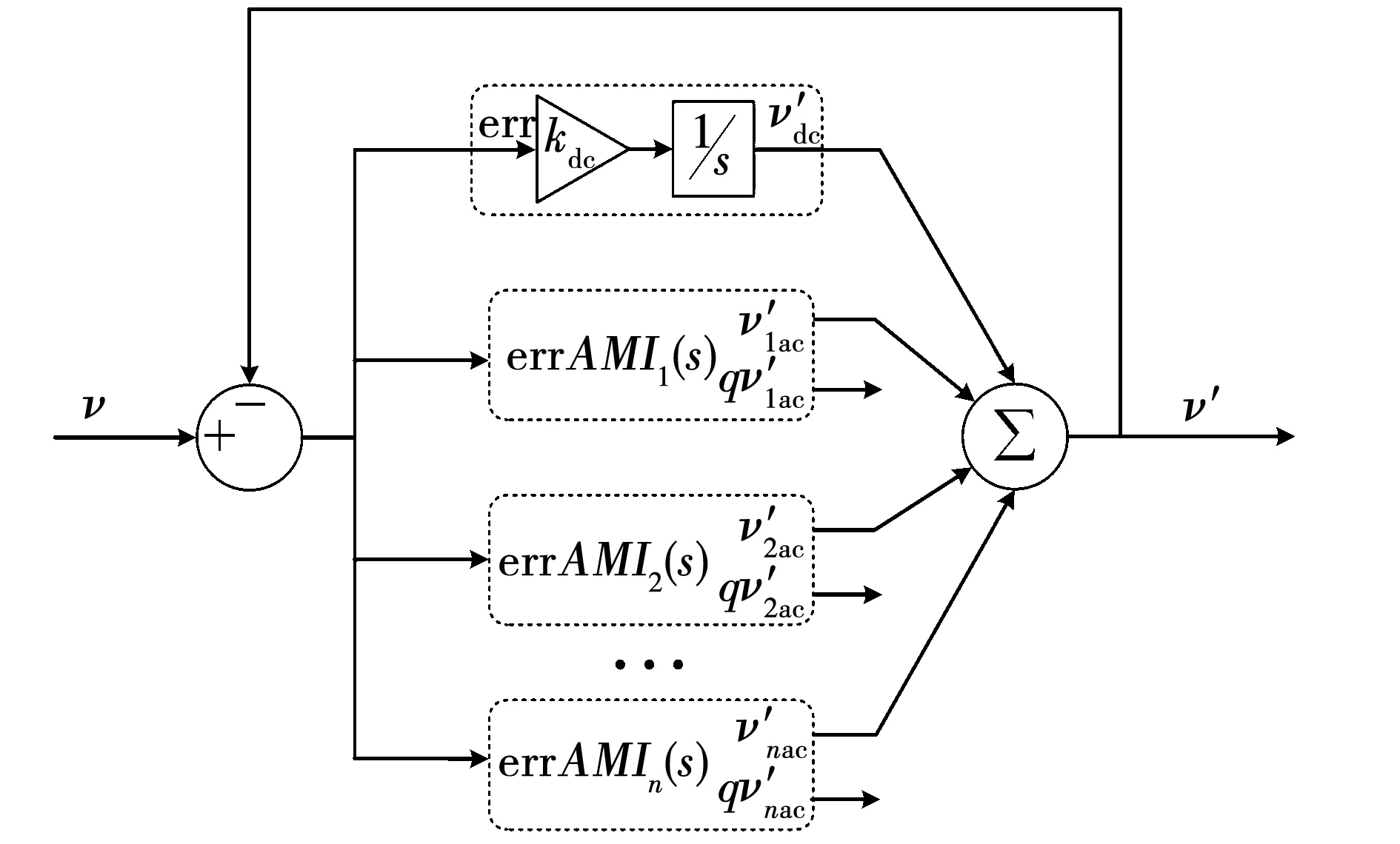
图12 提取直流和谐波分量的多个AMI-QSG(MAMI-QSG)结构Fig.12 Structure multiple AMI-QSG (MAMI-QSG) with DC and harmonics extraction

3 实验结果

实验装置由电网模拟器Chroma 61845、dSPACE DS1007平台、DS2004高速A/D板、DS2102高分辨率D/A板和电压传感器板组成。电网模拟器用于生成所需的电压，然后由电压传感器板进行采样检测，采样频率设定为10 kHz，再由DS2004 A/D板将其转换成数字信号送入DS1007平台，需要验证的算法可以在dSPACE平台上实现。dSPACE的处理结果将通过DS2102 D/A板将预估的变量转换为模拟信号，最终将波形显示在示波器中。

为了验证所提出的AMI-QSG结构的性能，实验分别测试了AMI-QSG与传统GI-QSG对正弦输入信号的动态响应，测量波形如图13所示。实验结果表明，AMI-QSG相比于GI-QSG有更快的响应速度，从而证明了AMI-QSG结构的优越性。

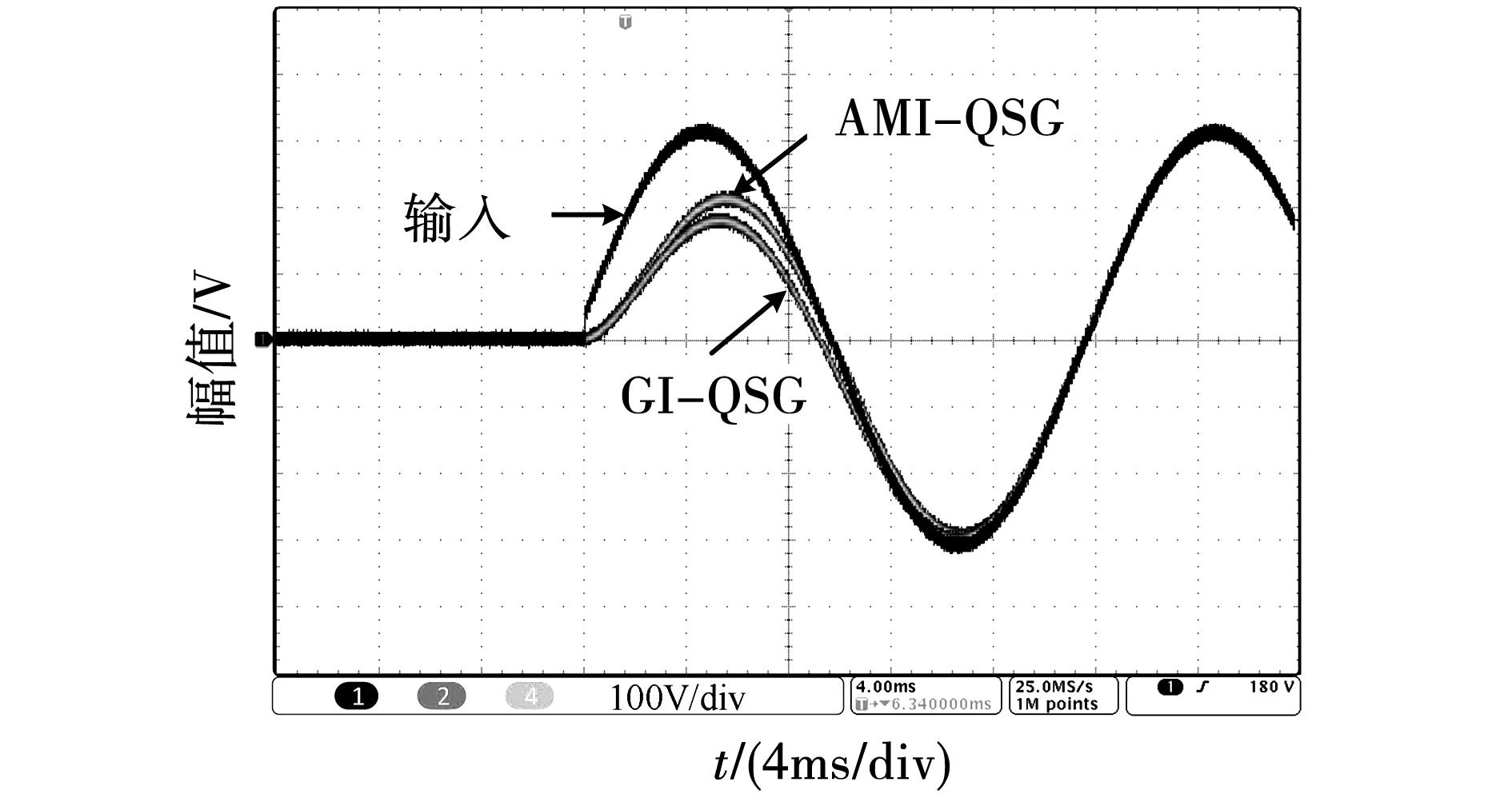
图13 输入正弦信号时，AMI-QSG与GI-QSG的 响应波形Fig.13 Response waveforms of AMI-QSG and GI-QSG when the input is sinusoidal signal

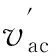
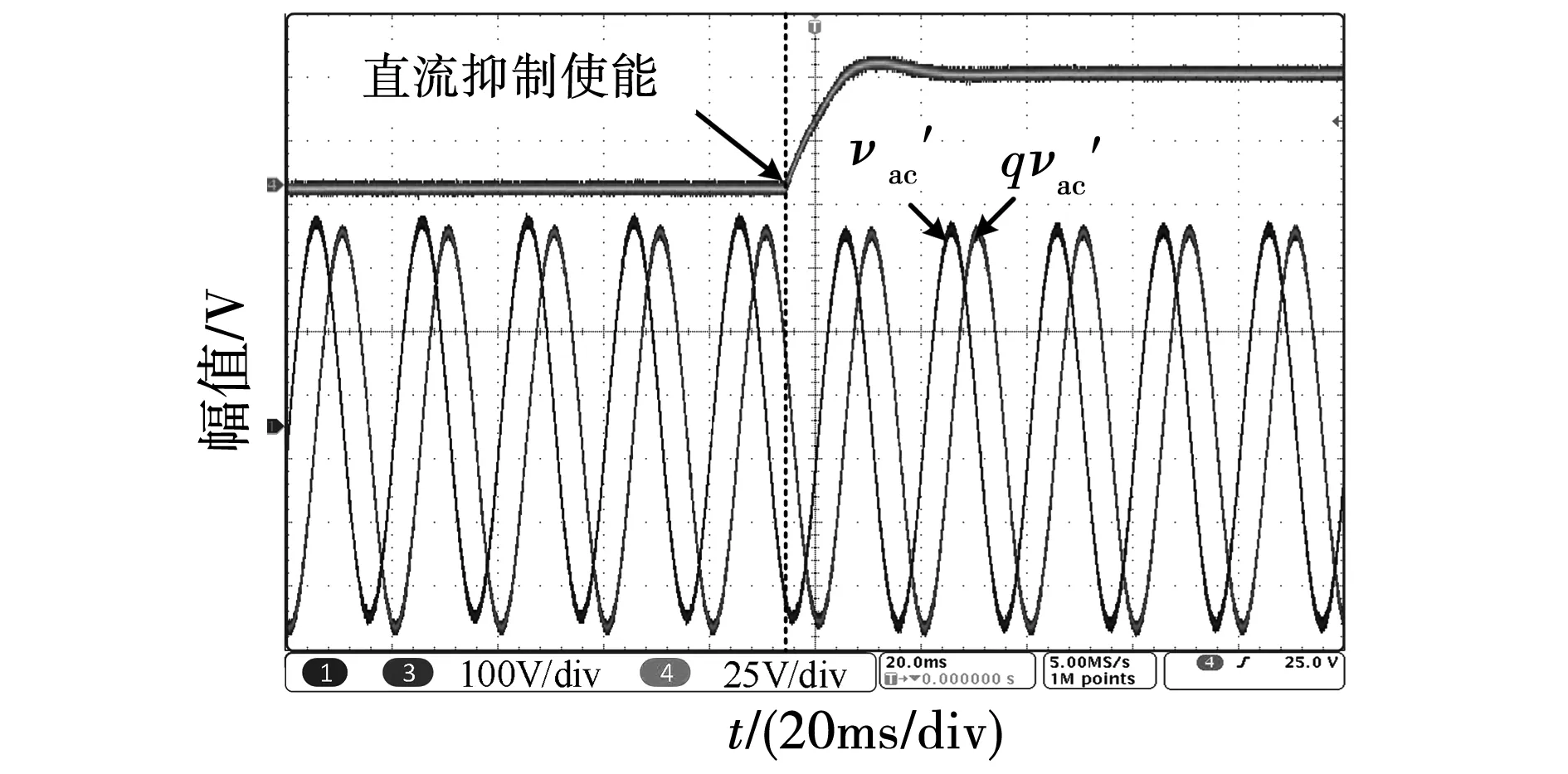
图14 AMI-QSG与改进的AMI-QSG在输入信号含有直流分量时的性能比较Fig.14 Performance comparison of the AMI-QSG and the improved AMI-QSG when the input signal contains dc component

为了验证MAMI-QSG对谐波提取的有效性，实验验证了实际情况中电网电压包含多种低次谐波分量的情况，并在输入信号中加入基波分量10%的3、5、7次谐波为例，首先对稳态性能进行测试，实验结果如图15所示。图15 (a)给出了输入信号的波形和MAMI-QSG中所有模块组合后的估计波形，可以看出估计波形与输入信号完全一致。除此之外，图15(b)进一步给出了由对应的AMI估计得到的基波分量和各次谐波分量。以上结果表明，所提出的MAMI-QSG具有良好的稳态性能。

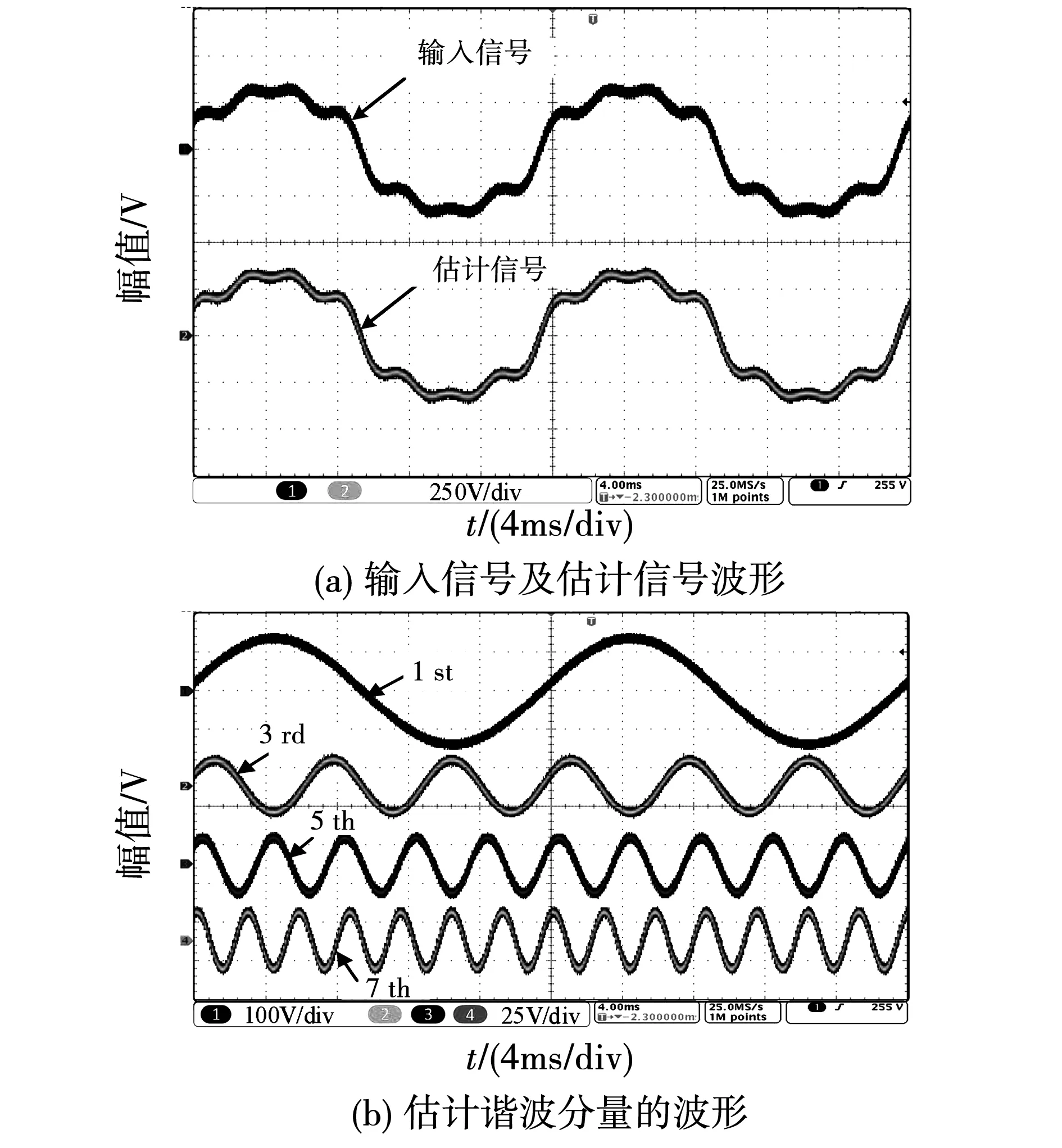
图15 存在谐波时MAMI-QSG的稳态性能Fig.15 Steady-state performance of the MAMI-QSG in the presence of harmonics

随后，在输入信号中包含相同谐波分量的情况下，测试了所提出的MAMI-QSG的动态性能，实验结果如图16所示。图16显示了所有分量的集成波形与输入信号波形的对比结果。可以看出，输出信号可以在0.02 s内快速跟随输入信号，从而验证了该方法的有效性。

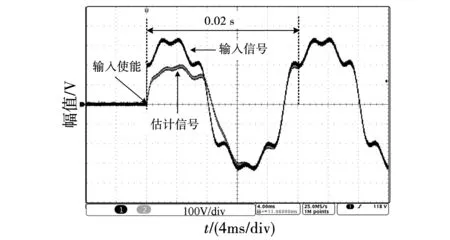
图16 MAMI-QSG在谐波存在时的输入信号和估计 信号波形Fig.16 Waveform of the input signal and the estimated signal of the MAMI-QSG in the presence of harmonics

4 结 论

本文从一阶系统的角度分析了GI-QSG动态响应，理论分析表明，由于GI幅值积分特性的影响，导致传统GI-QSG的动态响应设计规则不准确。为了克服GI-QSG这一缺点，本文提出一种更精确的幅度积分器 AMI-QSG。AMI-QSG的特性比GI-QSG更接近于FOS，因此可以参考FOS的动态响应参数设计规则来分析AMI-QSG的动态过程。除此之外，为了抑制输入信号中的直流分量以及提取其中的谐波分量，进一步改进AMI-QSG的结构，并通过实验验证了所提方法的有效性。