高频变压器漏电感参数灵敏度分析及其半经验模型

陈彬，陈健，唐波，徐文洋，张晶

(1.湖北省输电线路工程技术研究中心，湖北 宜昌 443002；2.三峡大学 电气与新能源学院，湖北 宜昌 443002；3.中国电建集团昆明勘测设计研究院有限公司，昆明 650000)

0 引 言

基于磁耦合的大容量高压DC/DC变换器是实现大规模直流源互联、兆瓦级直流电压变换以及直流电网的关键设备[1-3]。高频变压器是DC/DC变换器的核心磁性元件，起到电气隔离和电压变换的功能[4]。现有高频变压器设计方法大多强调对漏电感的精确控制，利用漏电感作为谐振电路中的电感，实现DC/DC变换器的零电压开关(zero voltage switching，ZVS)，达到减小磁元件数量，提高系统功率密度的目的[5-6]。漏电感过大将会降低变换器输出的效率，漏电感过小则不能实现零电压开关[7-8]。因此，精确计算高频变压器的漏电感对于整个变换器的设计非常重要。

现有高频变压器漏电感参数计算方法主要可归纳为两类：有限元法与解析法。在有限元法计算方面，由于有限元法具有很高的计算精度[9]，该方法已被广泛用于验证变压器漏电感解析计算方法的准确性和漏电感等参数的仿真分析[10-13]。比如，2018年文献[12]采用有限元方法计算了高频变压器的漏电感参数，明确了绕组交叉换位对漏电感的影响；2019年潘超等人为了研究直流扰动下变压器的电磁特性，基于有限元法提取了变压器的动态漏电感矩阵和励磁电感矩阵，并基于此建立了变压器直流扰动模型，分析了电流、电感和磁通量的变化规律，以及变压器两侧动态漏电感的变化特性[13]。有限元法的优点在于计算精度高，可以对任意形状的绕组和导线进行研究，得到绕组区域电流密度和漏磁场分布，但是当执行高频变压器优化计算时，计算量非常大。

在解析法方面，2012年P.R.Wilson提出一种高频变压器漏电感的集中参数等效模型，通过电路仿真得到漏电感参数，该方法未能给出漏电感的解析表达式，只适用于电路仿真[14]。2013年M. Lambert提出了运用镜像法和矢量磁位解析式来计算变压器绕组的漏感，但需要足够的镜像层数，才能保证该方法的计算精度[15]。2015年W. G. Hurley针对同轴线圈之间空气中的自感和互感，提出一种线元积分方法，但是只适用于互感绕组、无芯变压器以及无线能量传输等领域[16]。2016年律方成等人提出了一种基于磁链分区的大功率中频变压器漏电感参数的解析计算方法，但该类方法主要针对两个同轴布置的绕组，该方法只考虑了轴向漏磁，未考虑绕组的端部效应[17]。由此可知，以往对高频变压器漏电感的计算需要假定磁场是一维变量。对于高电压、大容量、高频率应用场合，由于绕组端部与铁心窗口的距离较大，绕组端部的磁场强度会出现明显的水平分量，即端部效应，磁场一维分布假设不再成立。变压器的运行频率越高，绕组的端部效应会越明显，造成漏电感的过高估算[18]。

近几年来，许多国内外学者已将半经验计算方法应用于高频变压器的参数计算[19-21]。比如，文献[19]和文献[20]均采用了半经验计算方法对高频变压器交流电阻系数进行计算，并通过与现有交流电阻计算方法以及实验结果进行对比，验证了半经验计算方法的精确性。此外，一些学者结合了有限元法与解析法，提出了高频变压器漏电感参数的半经验计算模型，并将该半经验模型应用于高频变压器的优化设计[21]。但是，上述模型的待定系数是基于静磁场求解方法算得的50 000组漏电感仿真结果拟合得到，这样并不能考虑高频条件下集肤效应和邻近效应对导体区域漏磁能量的影响。

为了精确并快速预估高频变压器的漏电感参数，本文在分析端部效应对漏磁场和漏磁能量影响的基础上，提出一种考虑端部效应的漏电感参数半经验计算方法。结合高频变压器的结构参数，可以快速获取高频变压器的漏电感参数。设计制作两台5 kHz、10 kW纳米晶合金芯式和壳式高频变压器试验模型，将该模型计算结果与现有解析公式和实验测量结果进行对比，用于验证本文方法的有效性。最后，分析不同填充系数、不同导体结构以及不同绕组布置方式下半经验方法的适用性。

1 漏电感参数计算方法及端部效应的影响

1.1 漏电感参数计算方法

漏电感参数的计算方法有磁链法和能量法，磁链法是通过计算变压器的自感和互感来计算漏电感，而其精确度取决于自感和互感的计算精度，对于结构复杂的变压器，因为其互感难以获取足够精确的值，所以此方法具有一定的局限性[22]。而能量法是根据原副边绕组在空气中储存的漏磁能量来计算漏电感[23]。变压器漏电感的解析表达式为

(1)

式中：μ为绕组漏磁路的磁导率；I为流过变压器绕组的电流的有效值；H为漏磁场强度；V为漏磁路的体积。

根据是否考虑漏电感的频变特性推导了两种计算漏电感参数的解析计算公式[24-25]。

1)未考虑漏电感的频变特性，基于能量法以及箔片导体区域的线性漏磁场强度表达式，得到铁心窗口内漏磁能量和归算到原边侧的漏电感[24]分别为：

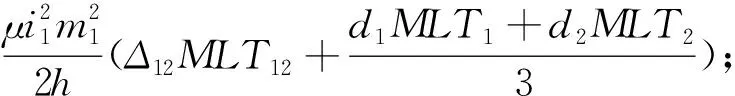
(2)

(3)

式中：MLT12、MLT1和MLT2分别为原副边绕组间、原边绕组和副边绕组的平均匝长；Δ12为原副边绕组的隔离间距；d1和d2分别为原副边绕组的厚度。

2)考虑漏电感的频变特性，对于箔片绕组，假设每层一匝，流过原副边绕组电流的有效值为I1、I2，层数为m1、m2，层间间距为dins1、dins2,平均匝长为MLT1、MLT2，原副边绕组隔离间距为diso，平均匝长为MLTiso，铁心窗口高度为hw。基于能量法以及箔片导体区域的频变漏磁场强度表达式，推导出了铁心窗口内各个部分的漏磁能量，如表1所示[25]。

表1 铁心窗口内各个部分漏磁能量

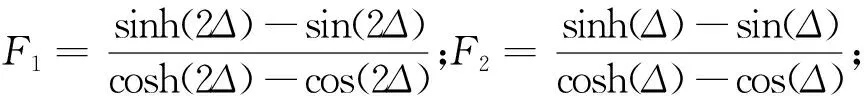
根据式(1)可得漏电感的解析表达式为

Lσ=2(Wiso+Wins1+Wins2+Wpp+Wss)/I2。

(4)

除了宽箔式绕组，高频变压器还可能采用窄箔片、矩形、方形或圆形等形状的绕组。根据变压器绕组有效导电截面积相等的原则，通过定义填充率，对绕组的电导率进行校正，将其它形状导体等效为与窗口等高宽箔片绕组，进而计算其漏电感参数[23]。

1.2 现有分析方法的局限性：端部效应

为了研究现有分析方法的局限性及其误差来源，建立高频变压器二维仿真模型，原副边绕组分别由单层、四层宽箔片绕组构成，如图1所示。改变宽箔片导体宽度，将绕组端部距离上下铁轭的垂直绝缘距离dcv设置为3、5和8 mm，采用有限元法计算铁心窗口内漏磁场、导体区域内电流密度分布以及铁心窗口内部的漏磁能量。图1给出了垂直绝缘距离为5 mm时铁心窗口的磁场强度和电流密度分布。由图1可知，在导线端部存在明显的横向磁场分量Hx。

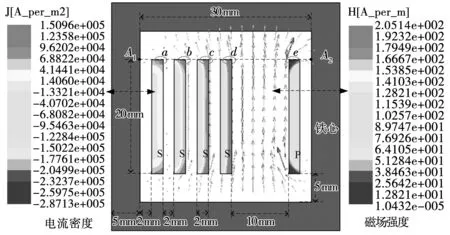
图1 端部效应对磁场和电流密度分布的影响Fig.1 Influence of edge effect on the distribution of magnetic field and current density

在有限元仿真软件中计算出绕组端部横向和纵向磁场分量沿A1A2方向的变化曲线，如图2所示。由图2可知，绕组端部存在横向磁场分量，并且当绕组的垂直绝缘距离增大时，绕组端部横向磁场分量逐渐增大，即端部效应更加明显。

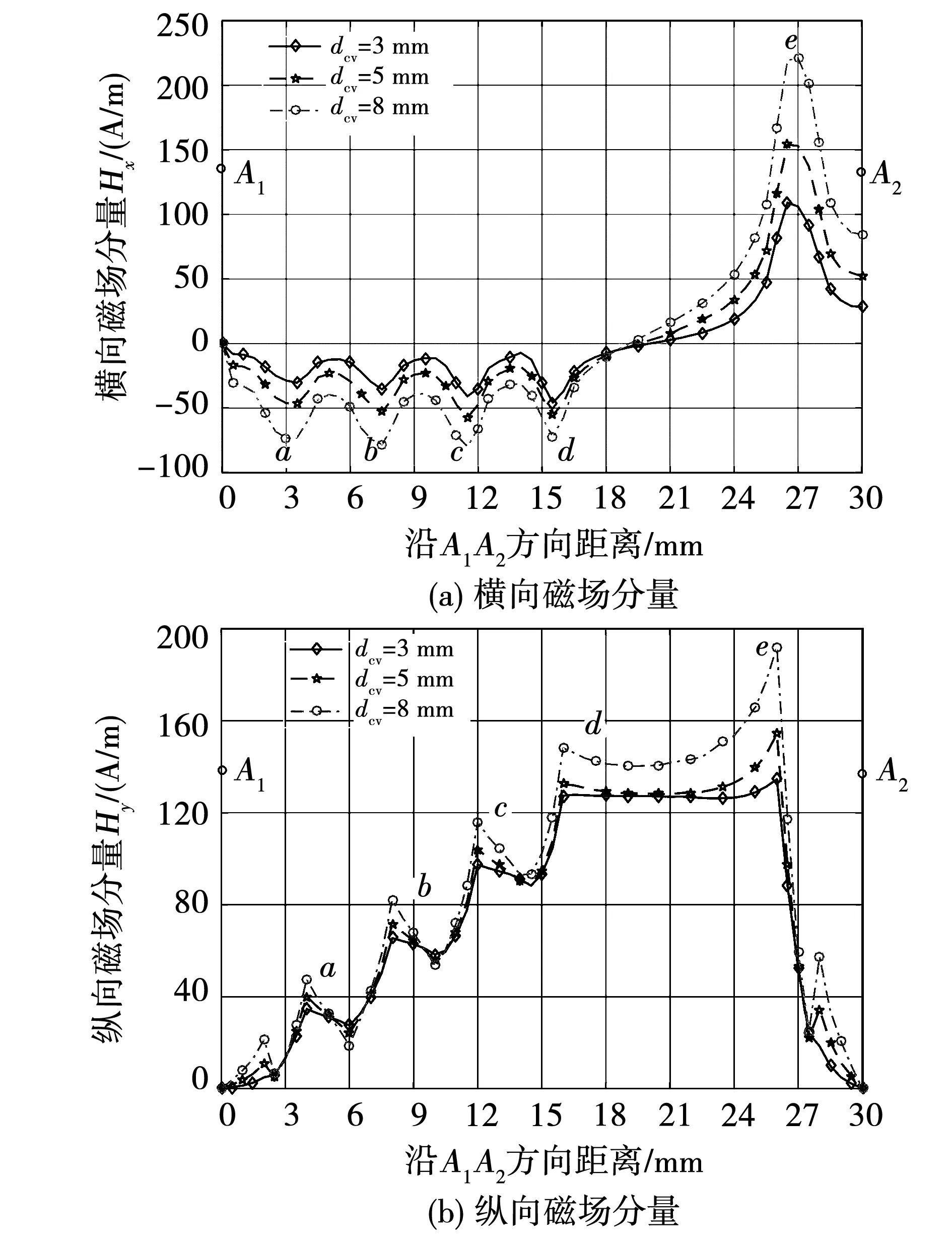
图2 绕组端部磁场强度分布Fig.2 Magnetic field intensity distribution at winding end

图3为有限元仿真和现有解析公式计算得到的单位长度漏磁能量随垂直绝缘距离dcv的变化情况。当dcv接近0的时候，考虑频变特性和未考虑频变特性的解析公式的偏差均在10%以下，然而随着dcv的逐渐增大，绕组的端部效应越来越明显，使得解析公式的偏差逐渐扩大，并且未考虑频变特性的解析公式偏差更大。因此，针对垂直绝缘距离较大的高频变压器，现有解析公式不能对漏电感参数进行精确计算。

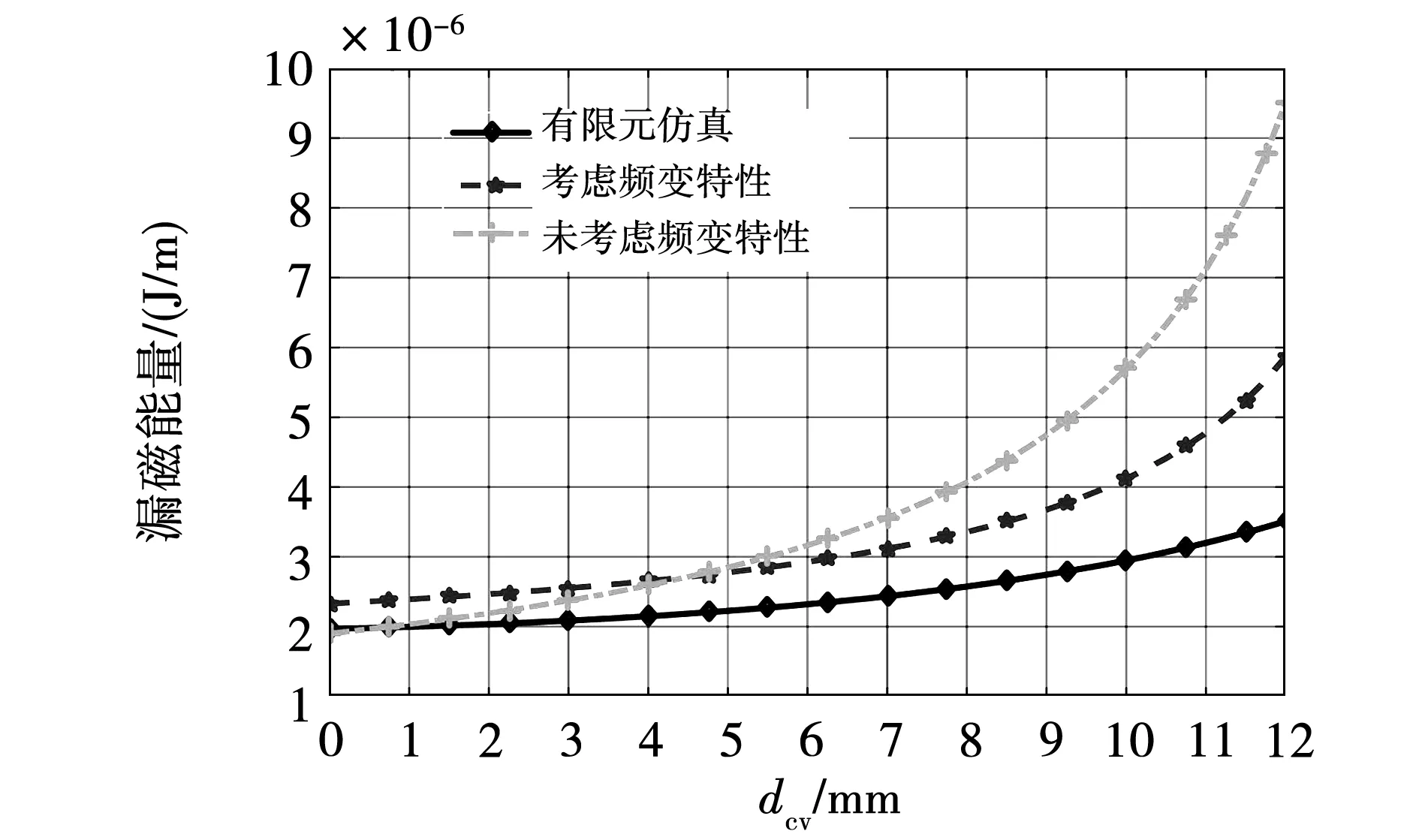
图3 不同垂直绝缘距离下现有解析公式与有限元仿真结果对比Fig.3 Leakage energy obtained by classical analytical formulae and finite element simulation with different vertical insulation distances

出于绝缘考虑，实际变压器绕组不可能占满整个铁心窗口高度，特别是对于大功率、高电压应用场合，导致不能完全满足磁场一维分布假设。有必要提出一种精确的考虑端部效应的漏电感计算方法，用于大功率高频变压器的精细化设计。

2 漏电感参数半经验计算方法

新方法的应用范围不能受限于特定类型的绕组结构(例如：矩形扁铜带、方形导体，单层或多层导体，不同填充率等)。除此之外，输入变量应该为一组无量纲化参量。提出的考虑端部效应影响的漏电感半经验公式的整体思想如图4所示，包括以下5步：1)确定控制漏电感或漏磁能量的决定性几何结构，见2.1节；2)组合决定性几何结构影响因子，进行无量纲化处理，并确定各个无量纲参量的合理变化区间，见2.2节；3)建立高频变压器的参数化有限元仿真模型，提取所有不同无量纲变压器组合情况下的漏磁能量，见2.3节；4)选择合适形式的基础拟合函数，并进行多变量回归分析，确定修正系数，见2.4节；5)将新方法的应用范围扩展至其它形状导体的绕组，如矩形扁铜线、方形等，并分析匝间距离对半解析公式计算精度的影响，见2.5节。

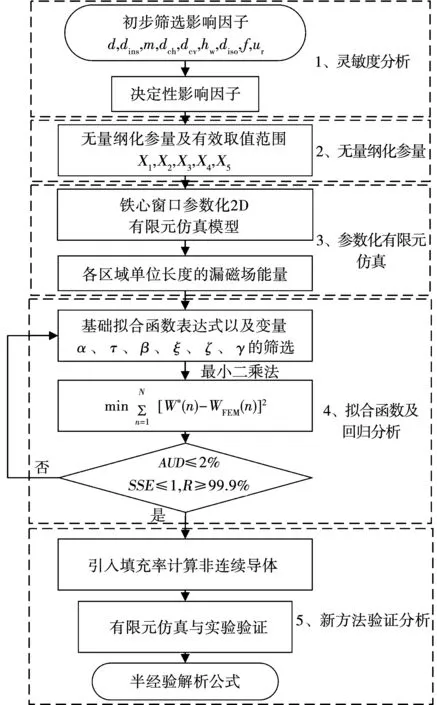
图4 半经验计算方法建立流程Fig.4 Approach to establish the semiempirical formula

在如下假设下，建立半经验计算方法：1)原副边绕组由相互平行且等厚度的直箔片组成；2)原副边绕组的端部距离上下铁轭的距离相等，并缠绕于高磁导率的铁心上；3)原副边绕组的安匝数相等；4)副边绕组位于零磁动势和最大磁动势之间；5)原边为单层导体(矩形实心导线或箔片)。

2.1 决定性影响因子筛选

半经验公式的待定系数和多变量回归分析的复杂程度完全依赖于自变量的数目。因此需要系统分析铁心窗口几何结构对漏磁能量W的影响规律，筛选出决定性影响因子。图5所示高频变压器铁心窗口的原副边绕组均由单匝箔片构成。铁心窗口结构可以由以下结构确定：箔片厚度d；绕组层间绝缘厚度dins；绕组层数m；副边绕组与铁心之间的水平间距dch；绕组与铁心之间的垂直间距dcv；隔离间距diso；铁心窗口高度hw。

由于变压器铁心窗口内外漏磁场的分布存在一些差异，为了更加精确地计算变压器铁心内外漏磁能量、明确变压器各区域漏磁能量对各个结构参数的灵敏度以及端部效应对各区域漏磁能量的影响关系，将图5(a)所示的变压器模型总的漏磁能量划分为铁心内部和铁心外部两个部分，而每个部分又可划分为绕组区域和隔离区域，如图5(b)、(c)所示。

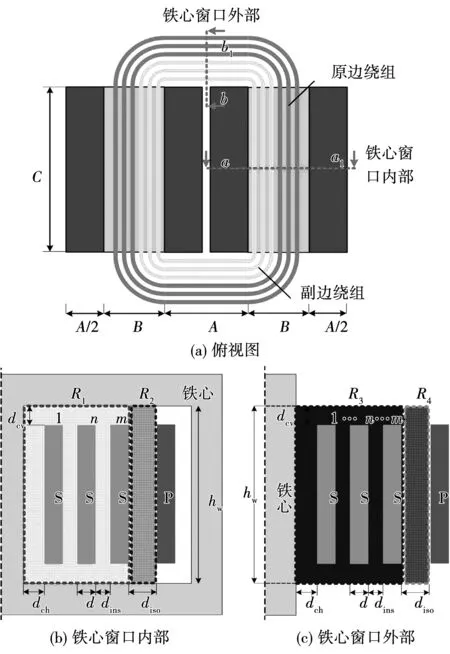
图5 铁心窗口几何结构因子定义Fig.5 Definition of geometric structure factors of the core window

由各个部分的漏磁能量解析表达式可知，箔片绕组漏磁能量取决于频率f和变压器的结构参数。借助控制变量法，分析单位长度漏磁能量Wm对变压器结构因子的灵敏度。值得注意的是，灵敏度分析是在f=5 kHz和hw=100 mm条件下进行，当频率f和铁心窗口高度hw改变时，漏磁能量对结构因子的灵敏度大小会发生改变，但并不会影响决定性影响因子的筛选结果。采用ANSYS/Maxwell电磁场仿真软件建立图5所示高频变压器二维仿真模型，利用有限元方法计算出单一结构因子在各个等间隔点处的漏磁能量，其余结构因子保持不变，计算出∂Wm/∂x的平均值。灵敏度的计算表达式为

(5)

式中：N为单个结构因子的等间隔点数目；xi为结构因子x在第i个间隔点处取值；WmFEM(xi)为对应于xi的漏磁能量仿真值。

图6显示了单位长度的漏磁能量在副边绕组5个不同层数下，结构因子x在变化范围内对Wm的灵敏度分析结果。由图可知，不同区域的漏磁能量受结构因子的影响是不同的，其中dch是影响最小的几何变量，因此该结构因子可以剔除。

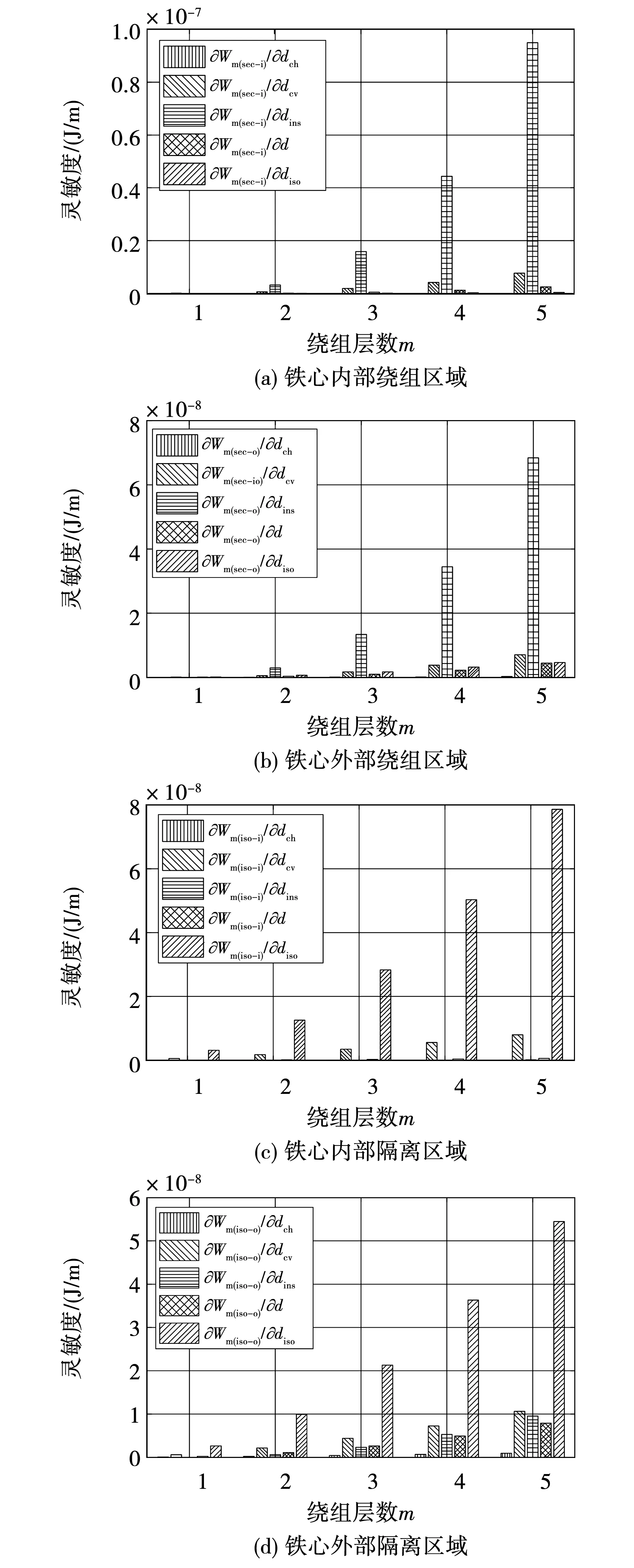
图6 铁心窗口几何变量的灵敏度Fig.6 Sensitivity of geometrical variables of the core window

除结构因子外，铁心相对磁导率μr对漏磁能量也可能存在影响。将有限元仿真模型的铁心相对磁导率分别设置为150(铁粉芯)、2 000(铁氧体)、15 000(非晶合金)和30 000(纳米晶)。结果表明，相对磁导率大小不会明显引起铁心窗口内磁场强度变化，并且漏电感值也不会发生显著变化。

2.2 无量纲化参量及其有效范围

从2.1节分析可知各个区域的漏磁能量与变压器结构参数密切相关，为了简化方程形式，消除原始变量量纲的影响。借助量纲分析方法，对2.1节筛选出的决定性影响因子进行无量纲化处理，最终确定5个无量纲化参量，如下：

(6)

利用上述5个无量纲参量，可以唯一确定图5所示铁心窗口结构。X1和X4类似于解析表达式中Δ和m。通过X2、X3和X5可以考虑dcv、diso和dins对漏电感参数的影响。

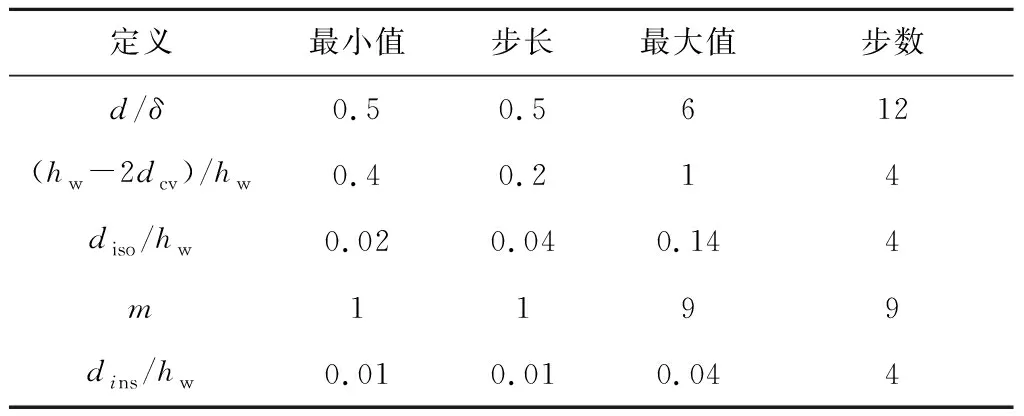
为了保证半经验公式的实用性，上述无量纲化参量的取值范围应该能够满足不同应用背景下高压高频变压器的设计要求。在电力电子变换器优化设计过程中，内部磁性元件的箔片绕组厚度近似等于集肤深度时，可降低集肤效应的影响，d/δ近似等于或略小于1。变换器中非正弦负载电流含有较多的奇次谐波分量，3次、5次等低阶次谐波幅值较大，其余各阶次谐波的幅值较小，可以忽略。因此，将参量X1的下限设置为0.5，上限设置为6，可以满足高频变压器绕组的设计要求。根据变压器设计的绝缘要求，将无量纲化参量(hw-2dcv)/hw、diso/hw和dins/hw的取值范围分别设置为0.4～1、0.02～0.14和0.01～0.04，可以满足高频变压器的绝缘设计。最终，确定的各个无量纲化参量的有效范围如表2所示。

表2 无量纲化参量及其有效范围

Table 2 Generic parameters with its corresponding

定义最小值步长最大值步数d/δ0.50.5612(hw-2dcv)/hw0.40.214diso/hw0.020.040.144m1199dins/hw0.010.010.044

2.3 参数化建模及有限元仿真

采用ANSYS/Maxwell电磁场仿真软件对图5所示高频变压器进行参数化建模。二维有限元模型的铁心窗口高度设置为hw=100 mm，在涡流场求解器中选择电流源激励，电流频率为5 kHz。在短路试验条件下，对箔片厚度d、绕组层间绝缘厚度dins、绕组层数m、原副边绕组间的绝缘间距diso、绕组与铁心之间的垂直间距dcv做参数扫描，在正弦电流激励且原副边绕组安匝数相等的条件下，计算不同设置值时各个区域单位长度的漏磁能量。由于导线区域存在集肤效应，在集肤效应层应进行加密剖分，集肤效应层以下的网格可以相对稀疏，将透入深度的剖分层数设置为6层，其余区域采用自适应剖分。

有限元模型中的参数化变量对应于2.1节中决定性影响因子(d,dcv,diso,m,dins)，各个参量的变化范围如表2所示。例如，对于无量纲参量X1，其取值范围为0.5～6(共12个取值)，可以通过改变箔片厚度d来实现，频率f及集肤深度δ保持不变(f=5 kHz)。类似地，保持铁心窗口高度不变(hw=100 mm)，改变dcv、diso、dins实现X2、X3、X5在各自有效范围内的取值。经过上述参数扫描计算，最终将得到20 592组不同绕组结构下单位长度的漏磁能量的有限元仿真值。

2.4 拟合函数及回归分析

该步骤需要确定一个基础拟合函数，通过多变量回归分析方法使拟合函数逼近仿真值。由于表1中漏磁能量计算公式考虑了集肤效应和邻近效应的影响，方程本身具有一定物理意义，且涉及了绕组层数m、归一化厚度Δ、dins/hw以及diso/hw4个无量纲参量。经过多次回归分析，最终确定的基础拟合函数如下：

1)绕组区域的基础拟合函数为

(7)

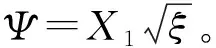
2)原副边绕组间隔离区域的基础拟合函数为

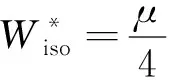
(8)

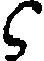
(9)

(10)

在参数扫描结果的基础上，待定系数Pij、Qi、Ji、Ti、Fij和Gij可以通过最小二乘法拟合得到，此时拟合值与有限元仿真值之差的平方和最小。

error(P、Q、J,T,F,G)=

(11)

根据图5所示变压器结构模型，将变压器漏磁能量划分为铁心内部和铁心外部两个部分，而每个部分又可划分为绕组区域和隔离区域。采用拟合软件对基础拟合函数在无量纲参量有效范围内进行多次拟合，最终其残差平方和(SSE)均小于1，相关系数(R)均大于99.9%，4个区域漏磁能量拟合曲线如图7所示。

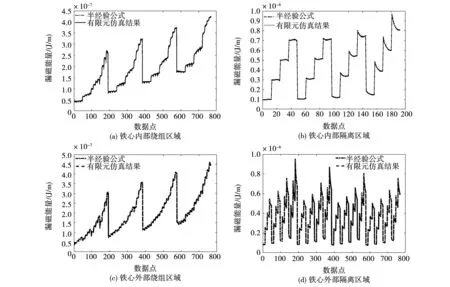
图7 漏磁能量拟合曲线Fig.7 Leakage magnetic field energy fitting curve

借助下式给出的相对偏差计算式，对半经验公式结果和仿真结果进行偏差分析，即：

(12)

式中：WFEM(i)为经过第i步参数扫描计算出的W仿真值；W*(i)为半经验公式计算值。

图8中(a)、(b)、(c)、(d)分别为变压器4个区域漏磁能量的全局相对偏差UD，其全局平均相对偏差AUD和全局最大相对偏差UDmax如表3所示。每个点对应于一种铁心窗口结构，其中红点代表半经验公式的相对偏差，而蓝点代表表1中漏磁能量公式的相对偏差，与圆心之间的距离反映了偏差的大小。由表3可知，半经验公式的计算精度高于式(4)给出的表1中漏磁能量公式。

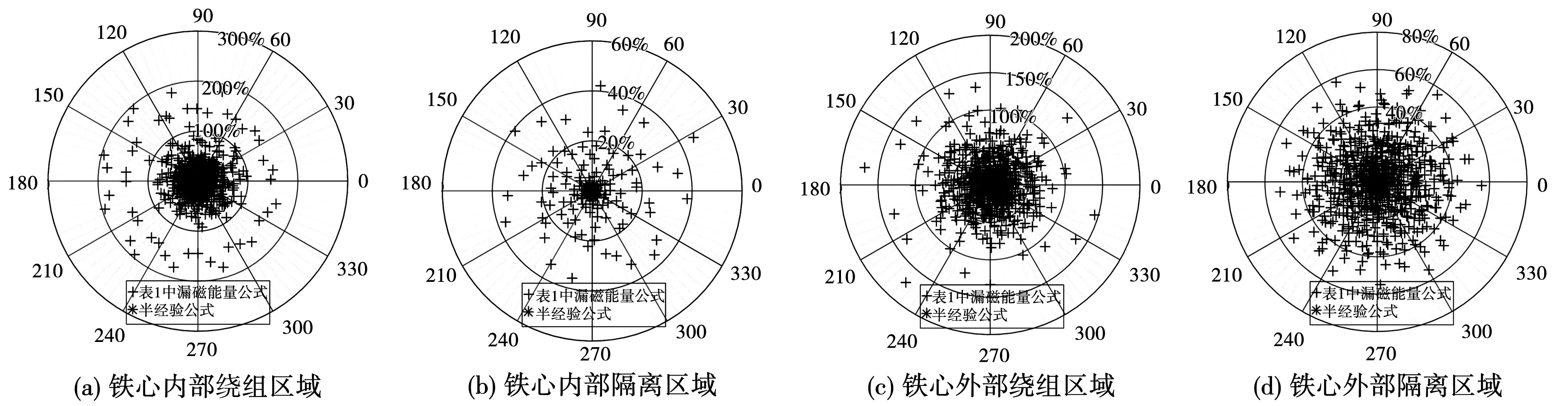
图8 半经验公式与表1中漏磁能量公式的全局计算精度比较Fig.8 Comparative accuracy overview between the semiempirical formula and traditional analytic formula

表3 全局计算精度比较

2.5 非连续导体的计算精度

前面已经推导了单箔片绕组的半经验公式，通过调整每层的填充率可以将半经验公式推广到其它形状导体的绕组，如矩形、方形等。紧密缠绕导体绕组的漏磁能量不同于稀疏缠绕导体绕组的漏磁能量。因此，将半经验公式应用于多孔导体层时，需要考虑匝间距离的影响。将无量纲参量X1按照下式进行修正，可以将半经验公式可以推广至矩形导体绕组，即

(13)

式中：d为矩形导体厚度；w为矩形导体宽度；v为同一层内相邻矩形导体的匝间距。

在均匀缠绕的分层绕组中，匝间距保持不变，匝间距v为矩形导体半厚度的5%～20%，等于2倍的导线自绝缘厚度。因此，将2v/d设置为0.05～0.2可以满足设计要求。其余无量纲参量的表达式(X1～X5)及其取值范围与箔片导体相同。

为了研究匝间距v对半经验公式计算精度的影响，建立了一台高频变压器仿真模型，原边绕组为单层矩形实心导线，副边绕组为四层矩形实心导线。匝间距的取值范围为0～0.1d。铁心窗口的其余几何结构如下：d/δ=0.5～6;每层匝数Nt=4;dcv=8 mm;dins=2 mm;diso=10 mm;hw=100 mm。以仿真结果为参照，图9给出了各个区域半经验公式的相对偏差。

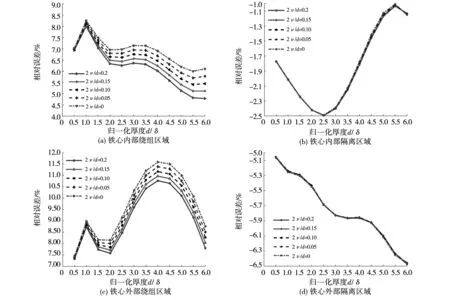
图9 不同匝间距情况下漏磁能量相对偏差Fig.9 Unsigned deviation in magnetic leakage energy for different interwire distance

结果表明：1)由图9(a)和(c)可知，匝间距的变化会对绕组区域的漏磁能量产生影响，并且当导体匝间距较大，导线排列较为稀疏时，相对偏差越小；2)由图9(b)和(d)可知，铁心内、外部隔离区域的漏磁能量受匝间距变化的影响较小；3)由图9(a)、(b)、(c)、(d)可知，推广后的半经验公式对于原副边绕组隔离区域的计算精度高于绕组区域的计算精度。

2.6 半经验公式应用举例

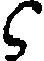
(14)

由式(14)可知，对于给定的变压器的各个组合变量取值均位于表2所示区间内。无量纲参量的计算结果如下：

(15)

表4 四层箔片绕组经验系数取值

图10(a)和(b)分别给出了半经验公式的铁心内部绕组区域和隔离区域单位长度的漏磁能量计算结果，并与仿真结果以及表1中漏磁能量公式进行比较，在整个dcv变化区间内半经验公式的计算精度高于表1中漏磁能量公式。

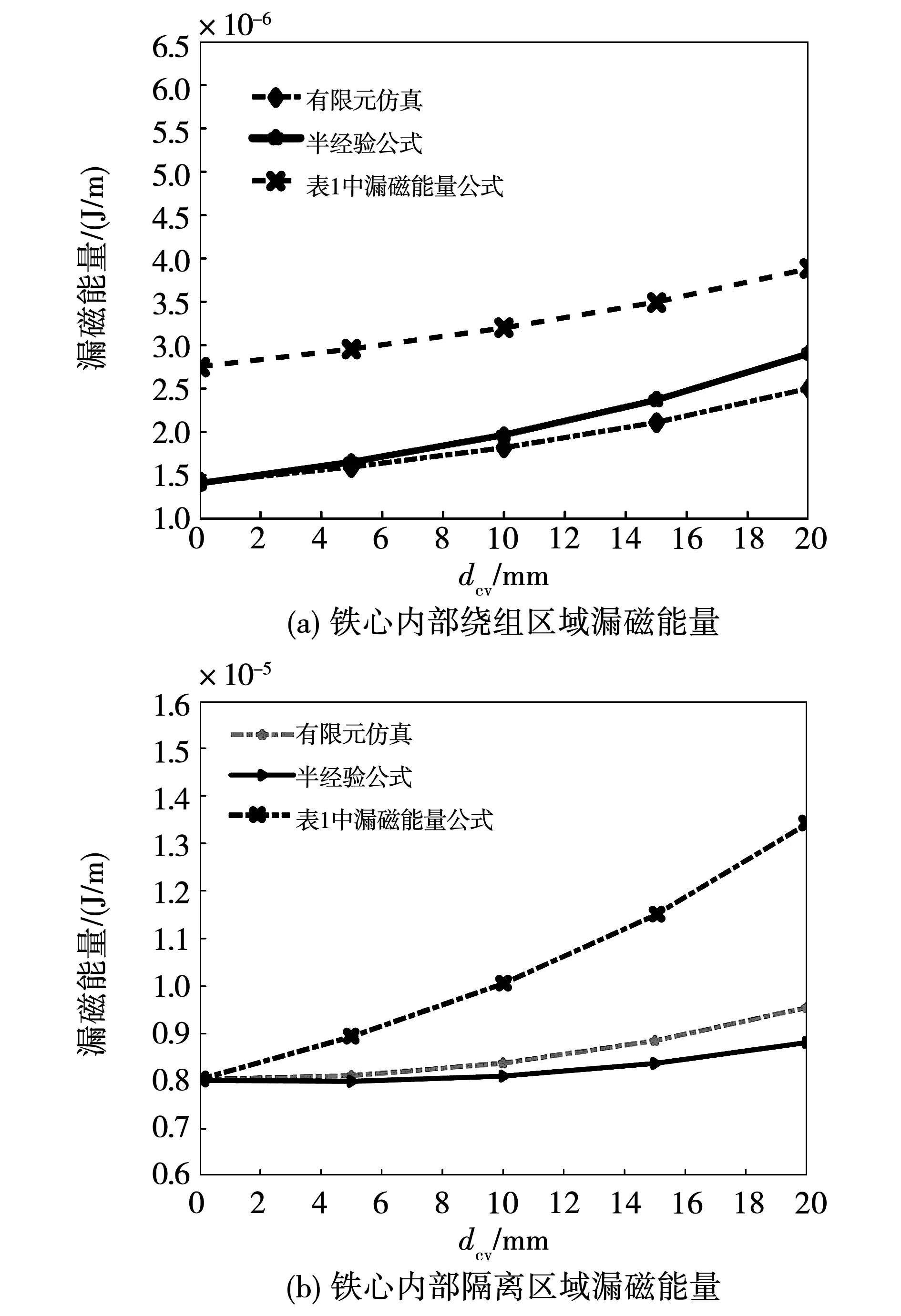
图10 四层矩形导线漏磁能量Fig.10 Magnetic leakage energy of four-layer rectangular conductor

3 试验模型与计算方法的验证

3.1 高频变压器试验模型

针对一台芯式和一台壳式高频变压器模型，分别采用新的半经验方法、表1中漏磁能量公式、有限元仿真方法和实验测量方法提取两台高频变压器的漏电感参数，用于研究所提方法的计算精度。两台变压器模型铁心材料为纳米晶合金，原副边绕组由矩形扁铜线绕制而成，容量为10 kW，电压等级为0.54 kV/0.54 kV，工作频率为5 kHz，二维结构图如图11所示，主要参数见表5所示[26]。

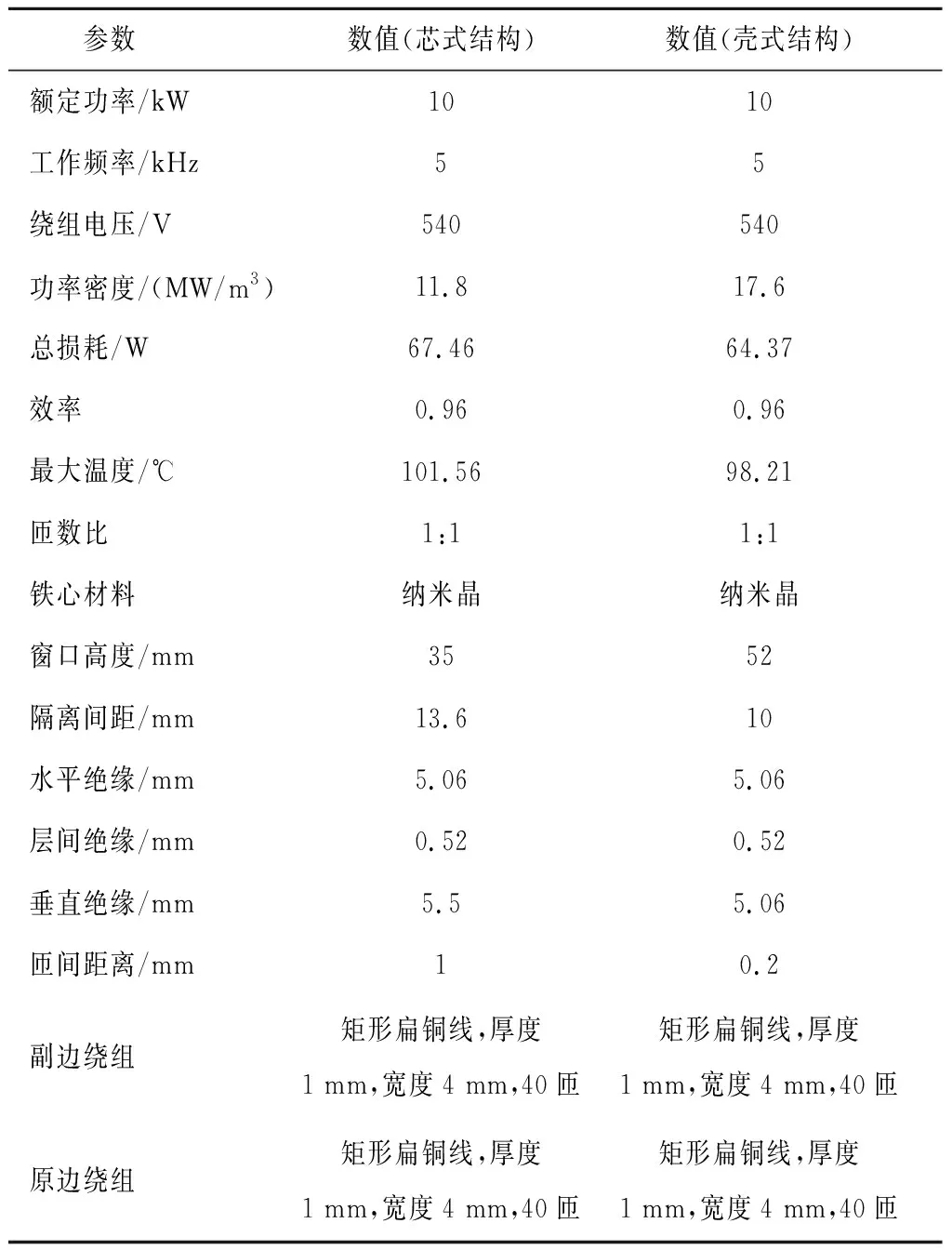
表5 高频变压器模型主要参数

图11 高频变压器试验模型Fig.11 HFT test models used in this paper

3.2 测量系统的搭建及漏电感参数测量

采用Agilent 4294A高精度阻抗分析仪对高频变压器试验模型的漏电感参数进行测量。测量频率范围为40 Hz～100 kHz，测量前进行开短路校准，提高测量结果的准确性。测量过程中施加低电平电流以确保变压器工作在线性区。由于将试验模型副边绕组短路，所测量得到的芯式和壳式变压器电感为归算到原边绕组的等效电感。图12为高频变压器漏电感测量平台。归算至原边绕组的漏电感测量结果如图13所示。由图13可知，频率等于5 kHz时芯式和壳式高频变压器模型的漏电感测量值分别为99.39 μH和99.06 μH。

图12 高频变压器漏电感测量平台Fig.12 Measuring platform for the leakage inductance of high frequency transformers

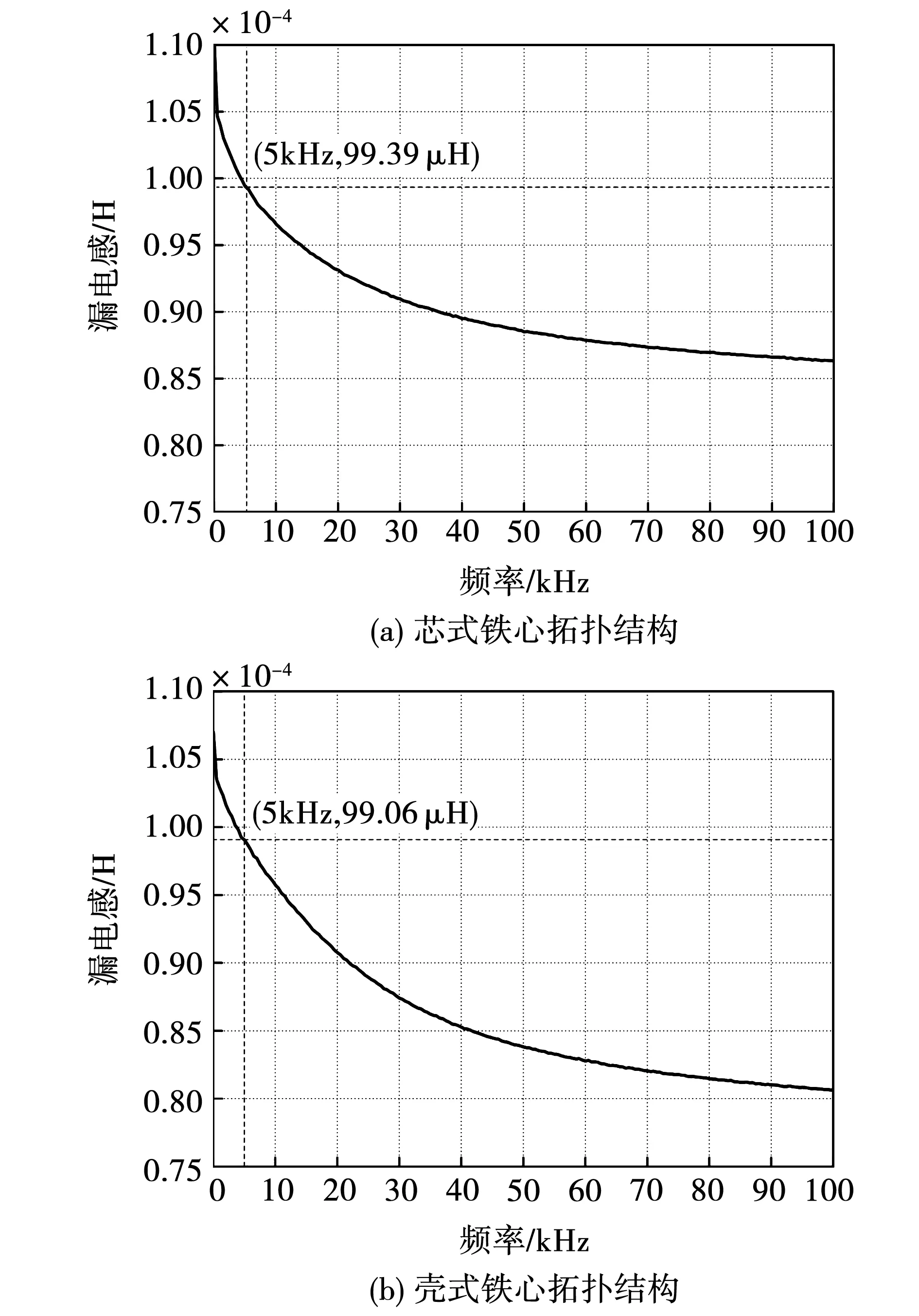
图13 归算至原边侧的漏电感测量值Fig.13 Measured values of leakage inductance referred to the primary side

3.3 结果比较与分析

表6列出了表1中漏磁能量公式、半经验公式与实验测量方法得到的频率5 kHz下芯式和壳式高频变压器模型的漏电感参数。由表6可知，以测量值为参考，表1中漏磁能量公式的计算值相对于测量值的偏差较大；半经验公式与测量值的偏差较小。由于表1中漏磁能量公式会高估漏电感参数，设计过程中如果采用表1中漏磁能量公式，将会造成高频变压器实物样机的漏电感低于设计值，无法实现漏电感参数的精确控制。

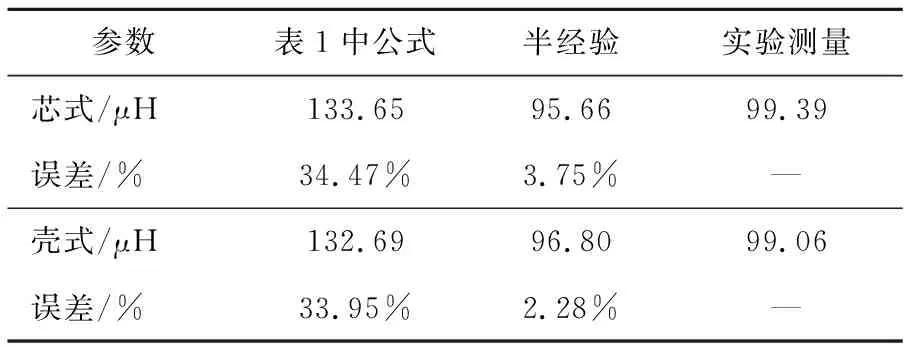
表6 芯式与壳式高频变压器模型漏电感参数

4 绕组布置方式的影响

交叉换位技术被广泛应用于高频变压器设计中，其优点是可以削弱邻近效应，减小磁性元件内的漏磁场强度和交流电阻值，进而减小漏电感和绕组损耗[27]。为了明确绕组布置方式对漏磁场强度的影响，检验新方法能否适用于不同绕组布置方式下漏磁能量的精确计算，建立了对应于4种绕组布置方式的高频变压器模型，如图14所示。

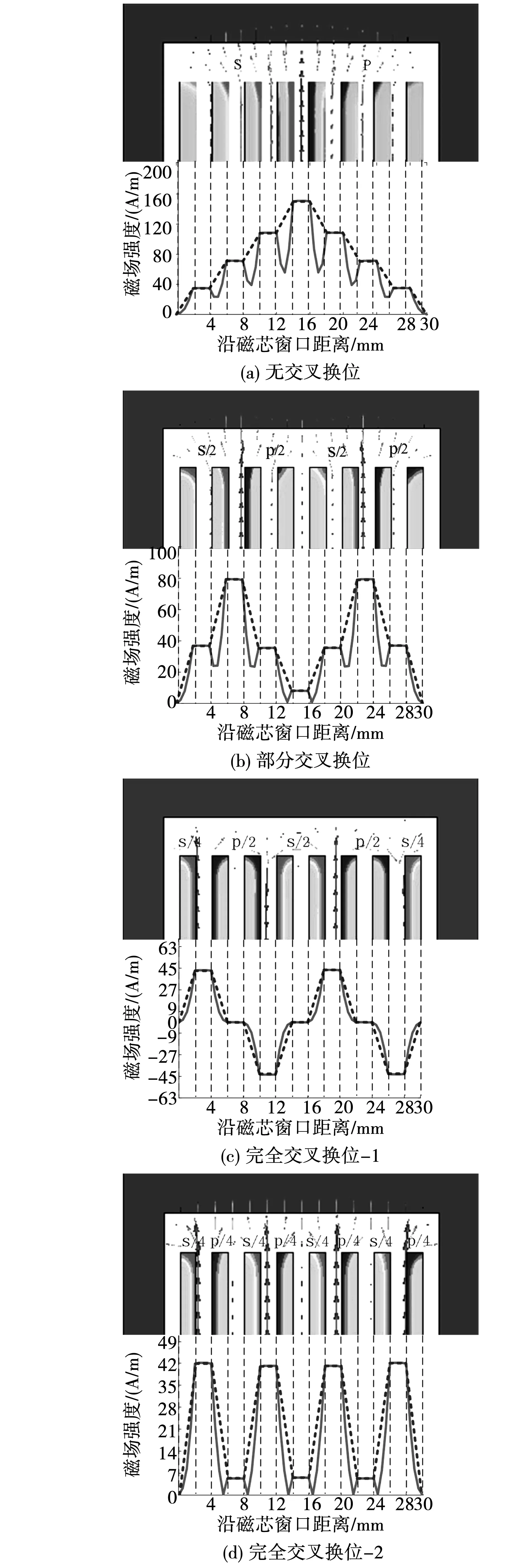
图14 四种绕组布置方式下漏磁场和电流密度分布Fig.14 Current density and leakage magnetic field distribution for four winding configurations

图14(a)为无交叉换位式，即原边绕组的所有层形成一组，副边绕组的所有层形成另一组，两个绕组电流方向相反；图14(b)为部分交叉换位式，即原副边绕组分别等分为m/2个部分(m为原副边绕组层数)，每部分包含两层绕组，每个部分绕组交替布置，相邻部分之间电流方向相反；图14(c)～(d)为完全交叉换位式，即原副边绕组各层交替布置。

以高频变压器的几何结构d=2 mm,m=4,dcv=0～10 mm,dins=2 mm,diso=2 mm,hw=30 mm为例进行分析。图14给出了铁心内部区域漏磁场H和原副边绕组导体区域的电流密度J分布，同时给出了5 kHz高频和100 Hz低频条件下沿铁心窗口方向的漏磁场强度。由图14可知，部分交叉换位后，由于邻近效应受到削弱，绝缘层区域的最大漏磁场强度减小一半；完全交叉换位后邻近效应几乎全部消除，对于每一层绕组，漏磁场强度和电流密度分布均相同，每一层和单层绕组一样，漏磁能量也相同。

4种绕组布置方式下，铁心窗口内部漏磁能量的表1中漏磁能量公式、半经验公式和有限元仿真结果随垂直绝缘距离dcv的变化如图15所示。表7具体分析了垂直绝缘距离dcv=5 mm时，半经验公式和表1中漏磁能量公式对于有限元仿真结果的相对偏差。结果表明：1)以有限元仿真结果为参照，半经验公式得到的漏磁能量与有限元仿真结果偏差远小于表1中漏磁能量公式；2)绕组按照部分交叉换位方式布置可以降低漏磁能量，进而降低绕组漏电感参数；3)绕组采用两种完全交叉换位布置方式可以进一步降低漏磁能量。

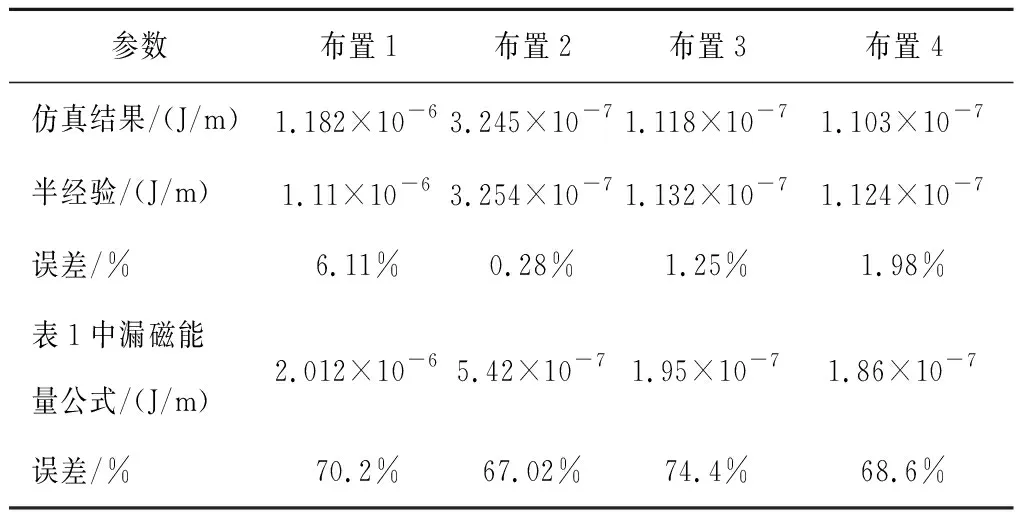
表7 4种绕组布置方式下相对偏差

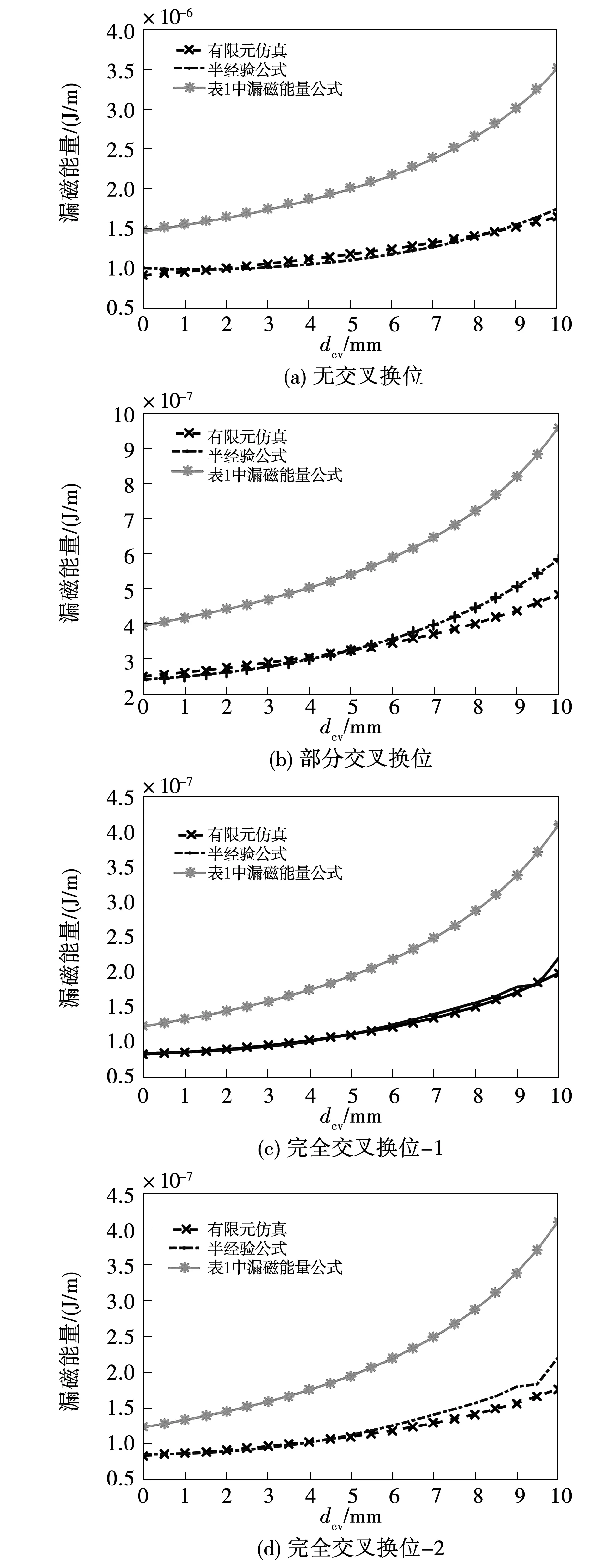
图15 四种绕组布置方式下的漏磁能量Fig.15 Leakage magnetic field energy for four winding configurations

5 结 论

1)在详细分析端部效应对漏磁场强度、漏磁能量影响的基础上，提出了一种新的考虑端部效应的漏电感半经验计算方法，其全局平均相对偏差为1.149%，全局最大平均相对偏差为11.5%，适用于高压高频电力变压器多层绕组的漏电感精确求解。

2)半经验计算方法中选取的决定性影响因子及取值区间，使该方法能够满足不同用途的高频变压器的精细化设计。新方法适用于窄箔片、矩形导体在不同填充率和布置方式下的漏电感参数计算，明确了绕组布置方式对漏电感参数的影响规律。

3)制作了5 kHz、10 kW纳米晶芯式和壳式铁心高频变压器模型，借助实验测量方法提取了两台变压器模型的漏电感，新方法的精度远远高于表1中漏磁能量公式，验证了本文新方法可以满足工程分析和设计的要求。