转子结构优化削弱车用永磁同步电机振动噪音

钱喆，唐光华，王群京，李大伟，程义

(1.安徽大学 电气工程与自动化学院，合肥 230000；2.安徽大学 高节能电机及控制技术国家地方联合实验室，合肥 230601；3.安徽江淮汽车集团股份有限公司新能源汽车研究院，合肥 230022；4.安徽安凯汽车股份有限公司，合肥 230051)

0 引 言

内置式永磁同步电动机由于其高效率、高转矩密度、高功率密度等特点被广泛的应用于电动汽车、船舶、智能家电等领域。在这些应用中，由于客户对于舒适度的追求和实际的需要，电机能否安静稳定的运行成为一个重要选择指标，因此近年来永磁同步电动机的振动噪声问题引起了广泛的关注[1-5]。

径向电磁力加载在定子齿面引起定子铁心振动向外辐射噪声是中小功率电机电磁噪声的主要来源。文献[1-8]都对径向电磁力引起的振动和噪声给予了很大关注，其中文献[6-7]通过解析法揭示径向力引起电磁振动和噪声的机理并用有限元法加以验证。文献[9-10]研究了不同槽极配合下的电磁振动和噪声，文献[11-12]研究了径向电磁力的最低次谐波对振动的影响，文献[13]采用力变换模型分析了开槽定子上的力分布，研究发现高阶气隙力也能引起大振幅的低阶定子振动。

关于切向力对振动和噪声的影响，近来一些学者对切向电磁力进行了更加深入的研究并得出了一些结论。文献[14]发现切向电磁力对电机与减速器的集成系统影响较小，然而对减速器的影响较大。文献[15]通过揭示切向力诱发振动的机理。研究发现，切向力可以通过齿的杠杆臂效应使轭偏转，结果表明，由于杠杆臂效应较强，且力幅不太小，切向力对最终振动的贡献与径向力相当。文献[16]揭示了永磁同步电机的全局和局部力谐波及其对振动的影响，局部力(包括局部切向力和径向力)的主要作用是引起定子的径向振动，而整体齿槽转矩和转矩脉动在安装刚度较低时可能引起明显的横向运动。

除了对径向力和切向力的研究，考虑电流谐波和故障运行状态下电机的振动和噪声也是一个研究的热点。文献[17]推导了逆变器供电时电机振动噪声频谱中新增加的频率与变频器开关频率的关系表达式，样机噪声实测结果验证了解析推导的正确性。文献[18]推导了考虑不同类型电流谐波时径向电磁力的特性，研究了不同供电电流下的振动和噪声，并用电流谐波引起的最低空间阶力的幅值变化解释了噪声和振动峰值的变化规律。文献[19]研究了变频器驱动时内置式永磁同步电机恒转矩调速和弱磁调速时的振动噪声特性。文献[20]提出了一种多物理模型来预测变速范围内永磁同步电动机的电磁噪声和音质。文献[21]研究了转子动态偏心和静态偏心对电机振动和噪声的影响。文献[22]研究了模块化三相永磁同步电机在典型的两相开路故障(对称和不对称)下的径向力和振动特性。

选择适当的槽极配合可以显著的降低径向振动和噪声。但是，这种选择往往受到其它性能需求的限制，在确定控制方法和槽极配合后，可以通过优化电机结构有效削弱电机振动。转子斜极和定子斜槽可以有效削弱降低气隙中的磁场谐波，对电机的电磁振动和噪声有较好的抑制作用[23-24]，文献[23]研究了转子阶跃偏斜的永磁同步电动机的电磁振动和噪声特征，并进行了噪声实验。文献[25]就转子阶跃偏斜对内置式永磁同步电机振动噪声的影响进行了实验验证，证明了方法的有效性。文献[26]详细研究了定子斜槽对永磁同步电动机振动和噪声的影响机理，并进行了实验验证。

本文对一款新能源纯电动汽车用的8极48槽内置式永磁同步电机为研究对象，针对由电机低阶齿谐波引起的电磁力谐波造成的噪声较大问题，采用转子分段斜极和转子表面开辅助槽相结合的方法来削弱由电磁振动引起的电磁噪声。推导分段斜极情况下的径向力波解析模型，分析斜极削弱电机电磁噪音的原理，在此基础上通过转子开辅助槽进一步削弱电机的电磁噪声。建立电磁有限元和结构声场耦合模型进行仿真分析。搭建样机噪声实验品台进行噪声试验。

1 径向电磁力波解析计算

根据麦克斯韦应力张量法，在忽略切向磁通密度的情况下，定、转子谐波磁场产生的径向电磁力波可以表示为

(1)

式中：Fr为径向电磁力密度；Br和Bt是径向磁通密度和切向磁通密度。BR和BS分别是转子永磁体磁场和电枢反应磁场在气隙中的径向分量，μ0为真空磁导率。由式(1)可见，电磁力的来源主要是由于气隙磁场谐波的相互作用，于是对永磁同步电机电磁振动和噪声的分析可以转化为对气隙中电枢反应磁场及永磁体磁场的研究。

对于整数槽永磁同步电机，转子主极磁场产生的谐波次数为

μ=(2r+1)p。

(2)

式中r=0，1，2，…，定子绕组磁场产生的谐波次数为

v=(6k+1)p。

(3)

式中：k=0,±1,±2；p为电机极对数。电磁力波的空间阶数可以总结为n=μ±v，电机振动噪声的主要来源是由转子主极磁场μ次谐波与一阶和二阶磁导谐波相互作用引起的。齿谐波极对数可表示为Vi=p±iZ，i=1，2，…，因此对于8极48槽电机，定子一阶齿谐波为52和-44，实际上由一阶齿谐波v=52或v=-44和转子永磁体谐波磁场μ与定子槽数Z=48附近的两个μ=44、52次谐波相互作用产生的电磁力波是永磁同步电机在空载及负载情况下电磁噪声的主要来源。而电磁力波的最低非零阶为

rmin=GCD(Z/m,2p)。

(4)

式中：GCD为最大公约数函数；Z为定子槽数；m为相数。因此8极48槽的最低非零阶为8，电机电磁力引起的定子铁心变形和电磁力空间阶数的4次方成反比，对于r≥8的电磁力可以不用关注，而主要关注r=0 (也称为呼吸模态)[21]。主极磁场极对数μ与定子绕组磁场极对数v相互作用产生电磁力波空间阶数由表1所示，表中仅列出主要的力波阶数。

表1 电磁力波阶数

其中红框圈注为由一阶和二阶齿谐波和主极磁场极对数μ相互作用产生的最低非零阶和0阶电磁力波。由一阶齿谐波和二阶齿谐波产生的电机电磁噪音倍频由表2所示。

表2 主要噪音频次

2 转子结构优化削弱电磁噪声

2.1 转子分段斜极下电磁力波的解析计算

斜槽和斜极是降低齿谐波和抑制电机电磁振动和噪声的有效方法，对于永磁同步电机而言，都可以改善电机的输出性能同时改善电机电磁噪声，但与斜槽相比斜极工艺上更简单，且能够减小永磁体涡流损耗、提高抗去磁能力[24]。如图1所示转子分段错极的示意图。

图1 转子分段斜极示意图Fig.1 Diagram of rotor-step skewing

当未分段时不用考虑相邻转子间的轴向磁通作用，气隙磁场沿轴向不会发生变化。分段斜极后沿轴向变化的空载气隙磁密如图2所示。分段后不同转子台阶上方相邻区域的气隙磁场在周向上发生变化，因此对斜极后的每一段转子上的电磁力波密度相加求平均可得整个气隙区域的电磁力波密度平均值。

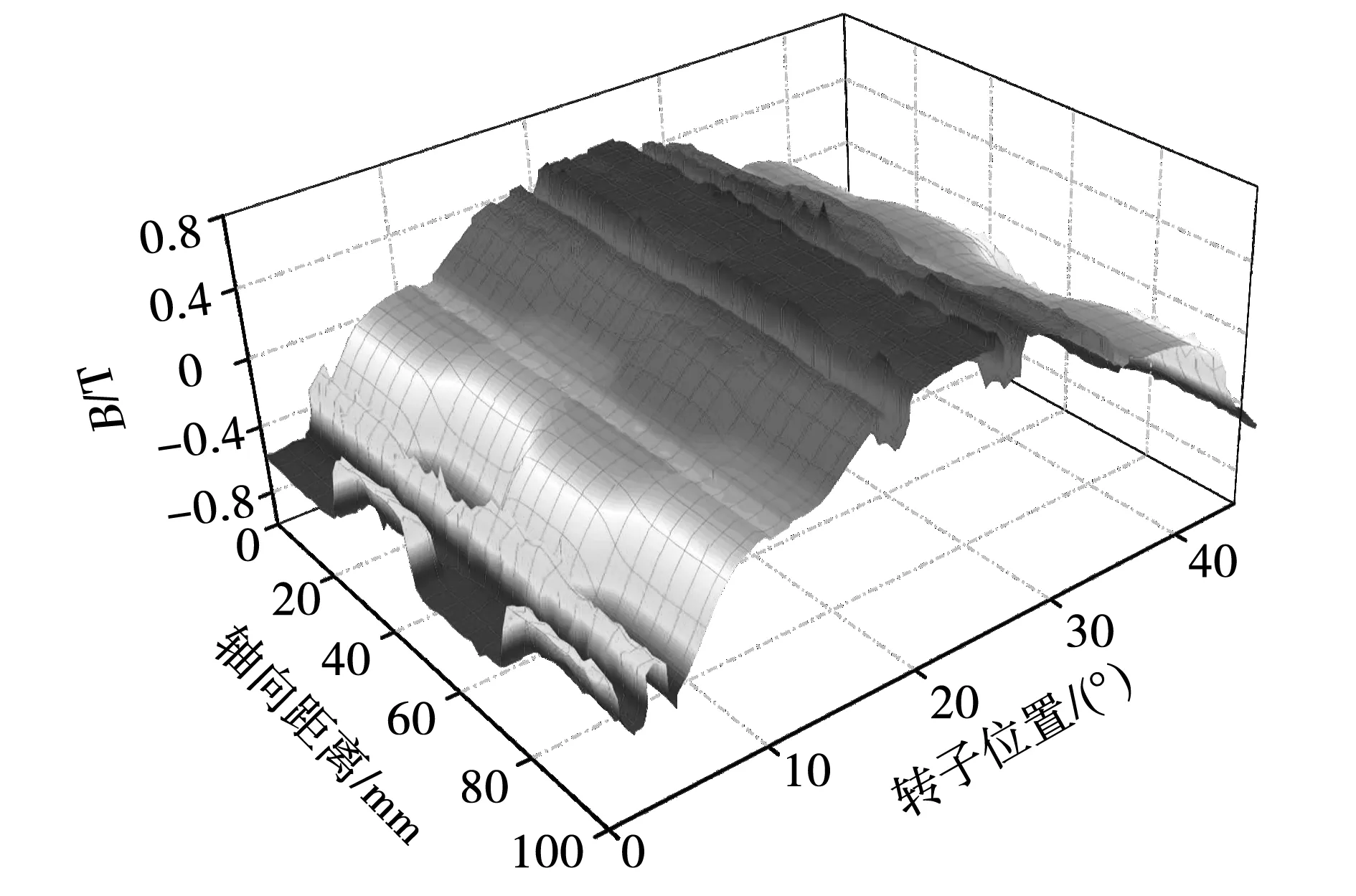
图2 空载气隙磁密Fig.2 Open-circuit flux density in the air-gap

转子分段斜极下的径向电磁力波由下面推导可得，如果转子永磁体分为j段，每一段在圆周上错开相同的角度γ，则第i永磁体产生的磁动势可以表示为

(5)

定子电枢反应产生的磁动势可表示为

(6)

其中：Fμ和Fv分别为永磁体和电枢反应磁动势谐波幅值；μ永磁体磁动势空间阶数；v为电枢反应磁动势空间阶数；θ是转子机械角度；t是时间；φv是相位角。

为了简化分析，忽略斜极对气隙磁导的影响，将单位面积上的气隙磁导函数表示为

(7)

式中：λ0、λk分别为磁导恒定分量和定子开槽调制引起的周期磁导分量；k为齿导谐波次数。

因此，考虑开槽效应下转子气隙磁通密度可由转子气隙磁动势乘以气隙磁导表达式得到

(8)

同理，电枢反应气隙磁通密度可表示为

(9)

对每一段的电磁力波密度迭加求平均可得到转子分段斜极后径向电磁力波密度的平均值，根据式(1)、(8)、(9)可以得到转子分段斜极后的径向电磁力波平均值[23]为

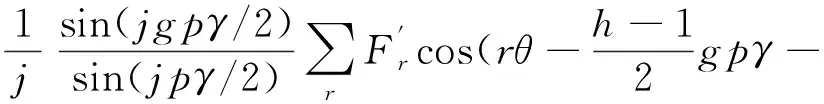
μωt+φr)。

(10)

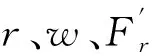
2.2 分段斜极降低电磁噪声机理分析

系统为线性时，定子铁心外表面静变形的形变量[24]可以表示为

(11)

式中：S为定子铁心表面积；h、m分别为定子刚度和质量；下标c、f分别为铁心和机壳。

因为阻尼系数δ的存在，定子表面的振动幅值可以表示为

V=Vs/([1-(fr/fm)2]2+[(fr/fm)δ/π]2)1/2。

(12)

式中fr、fm分别为径向力波频率和电机固有频率。转子分段斜极后声压的变化量可以表示为

ΔLp=20lgKsk。

(13)

由式(12)和式(13)可知，定子表面振动幅值与电磁力波成正比，电机斜极后的声压级与斜极系数的对数成正比。做好电机本体设计阶段工作能很大改善电机电磁性能和噪声性能，在电机加工装配好以后发现缺陷很难去弥补，因此，选择合适的斜极方式和磁路优化方案与电机的质量、刚度、阻尼等参数配合很重要。

图3所示为样机未斜极与分4段斜极，斜极机械角度为3.75°时0阶径向电磁力时间谐波傅里叶频谱图，如图当斜极后除了2次谐波分量稍有增大，4次到20次都有不同程度的削弱，特别是对于需要重点关注的12次谐波降低了53%，验证了分段斜极对径向电磁力谐波的削弱作用。

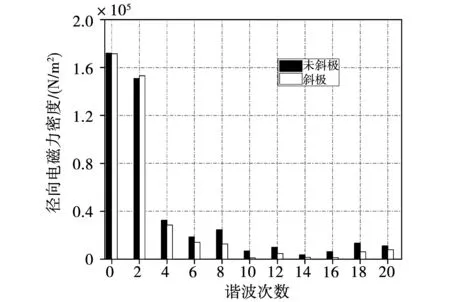
图3 径向电磁力密度时间谐波分解Fig.3 Temporal harmonic decomposition of radial electromagnetic force density

2.3 转子开辅助槽抑制电机振动噪声

针对本样机48倍频的电磁噪声较大，在转子分段斜极的基础上，进一步采用转子表面开辅助槽削弱由低阶齿谐波引起的径向电磁力产生的电磁噪声，如图4所示为电机转子辅助槽示意图。

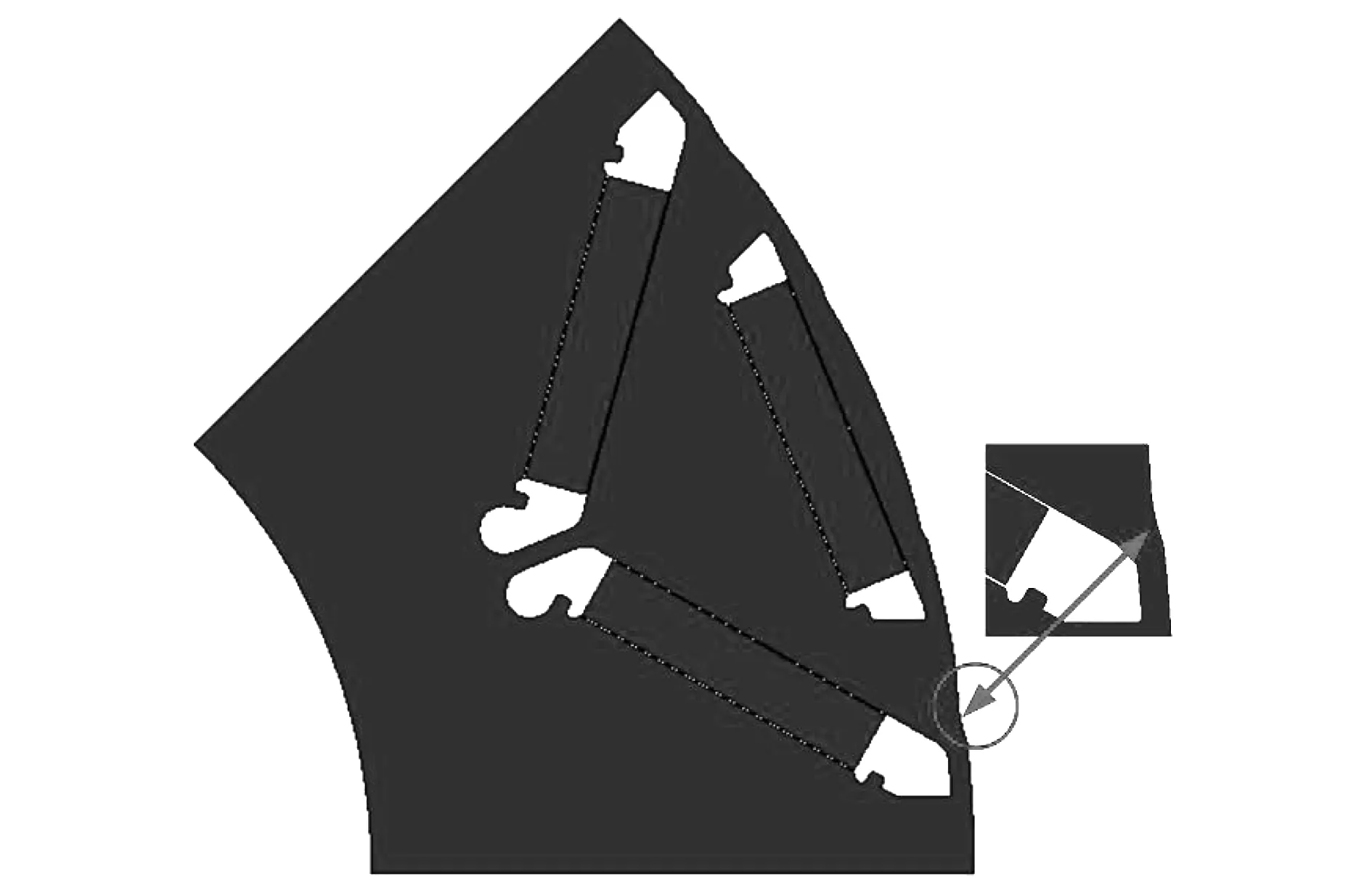
图4 转子开槽示意图Fig.4 Schematic diagram of rotor surface slotting

图5所示为样机转子表面未开辅助槽和开辅助槽时0阶径向电磁力时间谐波傅里叶频谱图，当开槽后6、16、18、20次谐波幅值有所增加，但对于需要关注的12次谐波削弱了23%，因此可配合转子分段斜极使用。

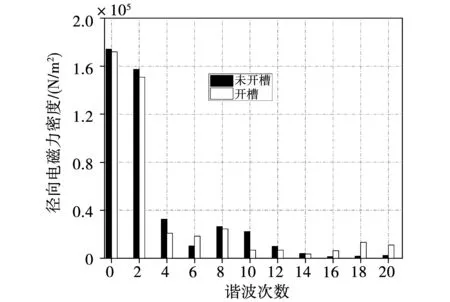
图5 径向电磁力密度时间谐波分解Fig.5 Temporal harmonic decomposition of radial electromagnetic force density

2.4 仿真分析对比

通过结构声场的耦合计算，可得到样机转子结构未优化时全转速下范围内噪声频谱的瀑布图，如图6所示，高噪声区主要集中在高转速区，这是因为在高转速区时，此时由齿谐波引起的0阶12f1电磁力频率较高接近电机定子的0阶固有频率，样机的0阶、8阶固有频率分别为7 410、15 600 Hz，满足共振条件。

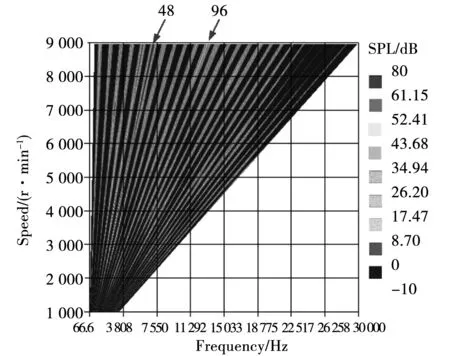
图6 全转速下噪声瀑布图Fig.6 Noise waterfall at full speed conditions

图7所示为电机在9 000 r/min、负载20 N·m、f1=600 Hz工况下的噪声频谱图，如图所示，当频率接近12f1时产生了最大噪声为80.99 dBA。这也符合了第1节中的分析结果。

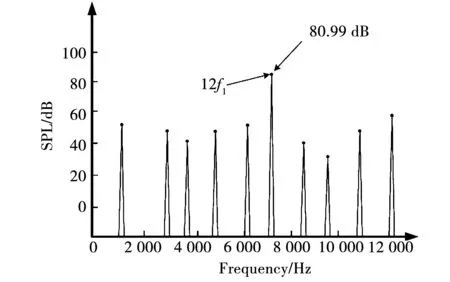
图7 9 000 r/min下的噪声频谱图Fig.7 Noise spectrum diagram at 9 000 r/min

考虑转子分段斜极情况下样机全转速下范围内噪声频谱的瀑布图如图8所示，图8和图6对比可见，通过转子分段斜极后，由0阶12f1阶电磁力波引起48倍频的电磁噪声在7 000 r/min到8 500 r/min处得到大幅度削减，斜极后7 000 r/min到8 500 r/min的噪声最大值相比于未斜极时，由80 dB降低到52 dB,这也和图3的分析结果吻合。

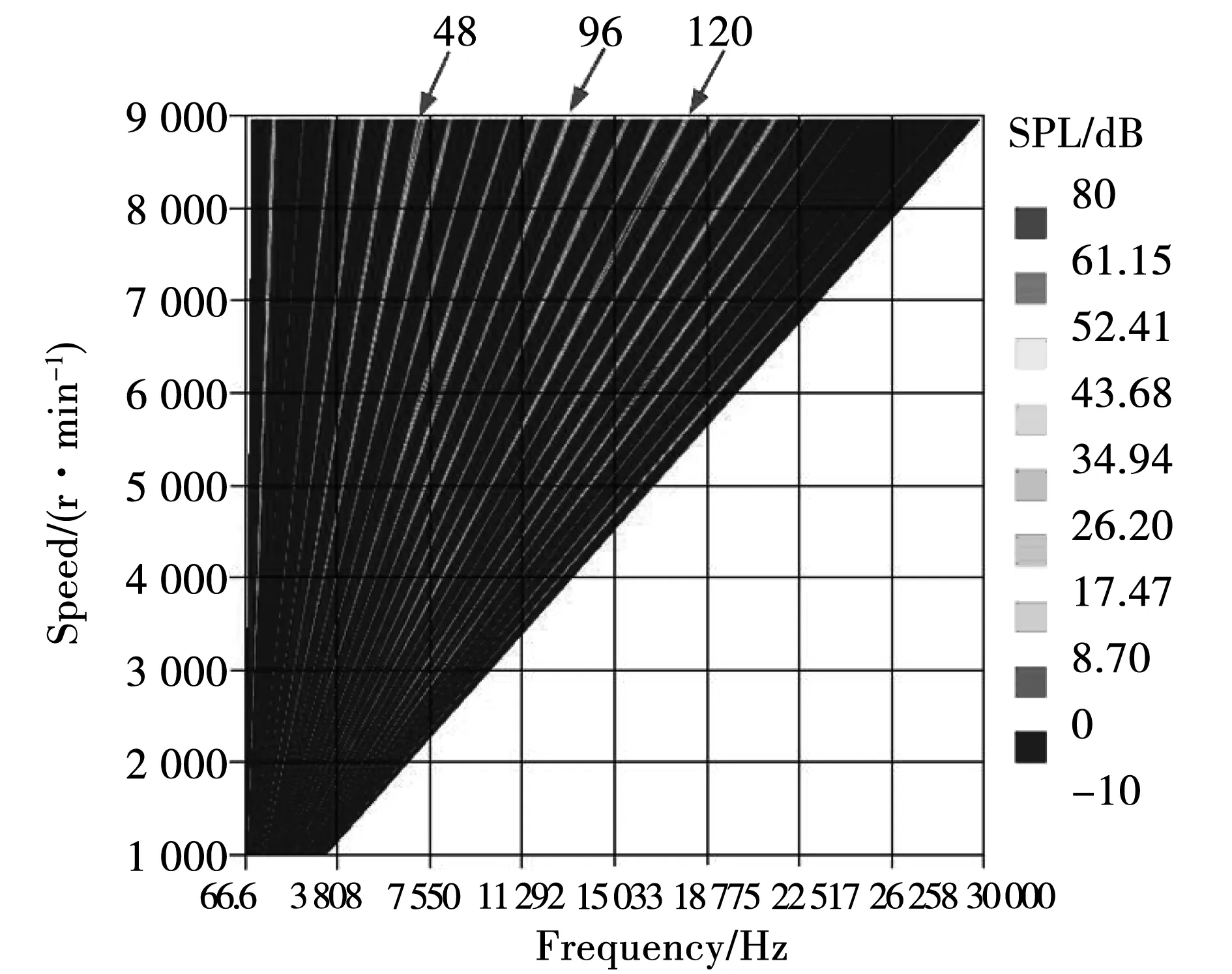
图8 转子分段斜极下全转速噪声瀑布图Fig.8 Noise waterfall diagram at full speed of rotor under rotor-step skewing

转子表面开辅助槽情况下样机全转速下范围内噪声频谱的瀑布图如图9所示。

图9和图6对比可见，通过转子表面开辅助槽后，由0阶12f1电磁力波引起48倍频的电磁噪声在7 000 r/m到8 000 r/min处得到大幅度削减，斜极后7 000 r/min到8 000 r/min的噪声最大值相比于未斜极时，由80 dB降低到了65 dB,这也和图5的分析结果吻合。因此仿真结果表明通过对电机转子结构进行优化能够有效的削弱由一阶齿谐波引起的0阶12f1产生的48倍频电磁噪声。

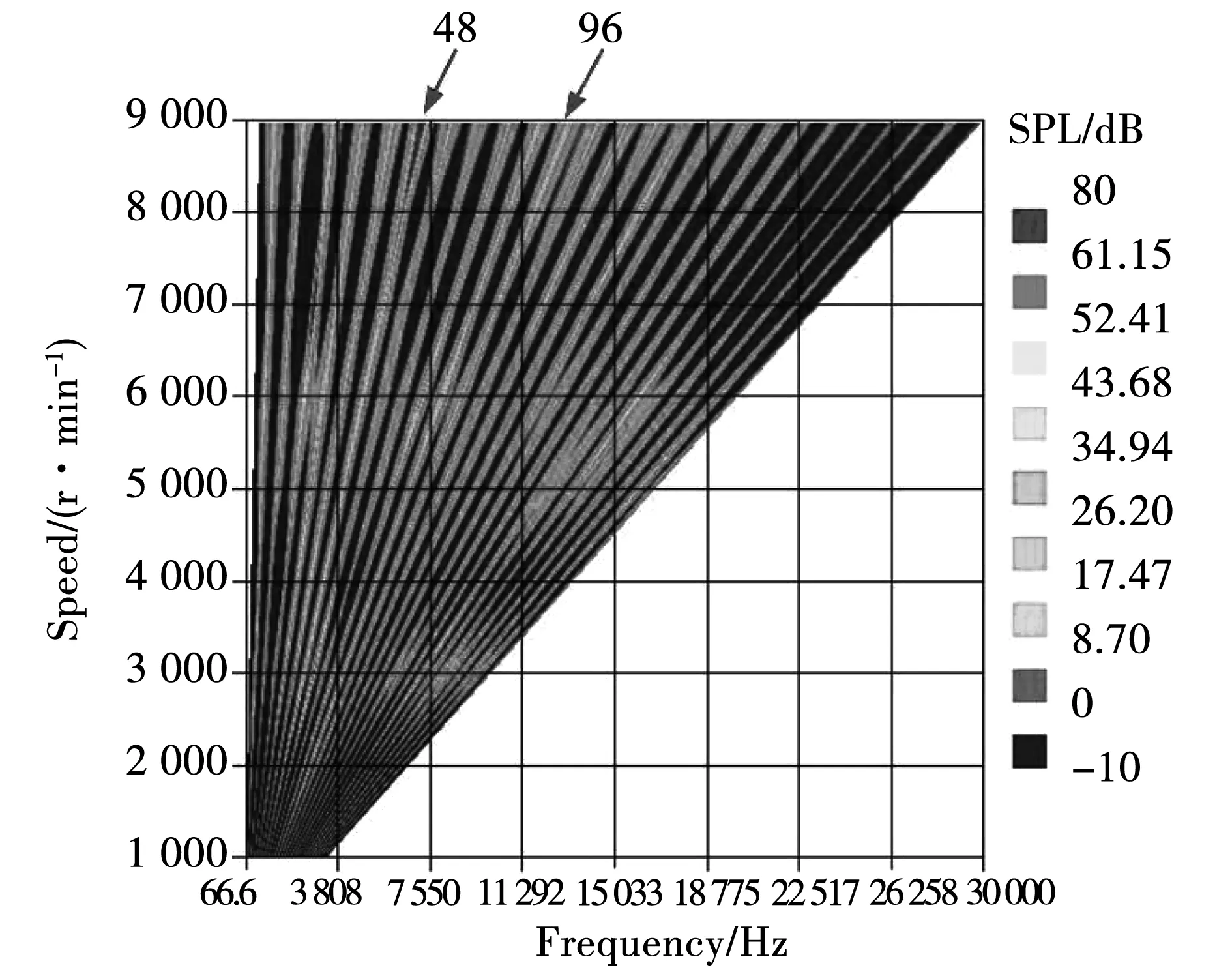
图9 转子表面开辅助槽全转速噪声瀑布图Fig.9 Full speed noise waterfall diagram under auxiliary slot on rotor surface

3 样机测试

图10为电机噪声实测图，在距离电机正上方0.3 m位置处放置麦克风，通过麦克风测试电机所辐射的噪声。

图10 样机噪声实测图Fig.10 Noise test experiment of prototype

图11和图12为电机空载和负载20 N·m时样机时测噪声瀑布图。由图6和图12的实测结果对比可以看出，通过对转子结构优化后，样机全转速下的噪声最大值由80 dB(A)下降到70 dB(A)，由于实验是处于半消音的环境下进行的，样机实测结果中高转速低频区的高噪声区是由测功机引起的。

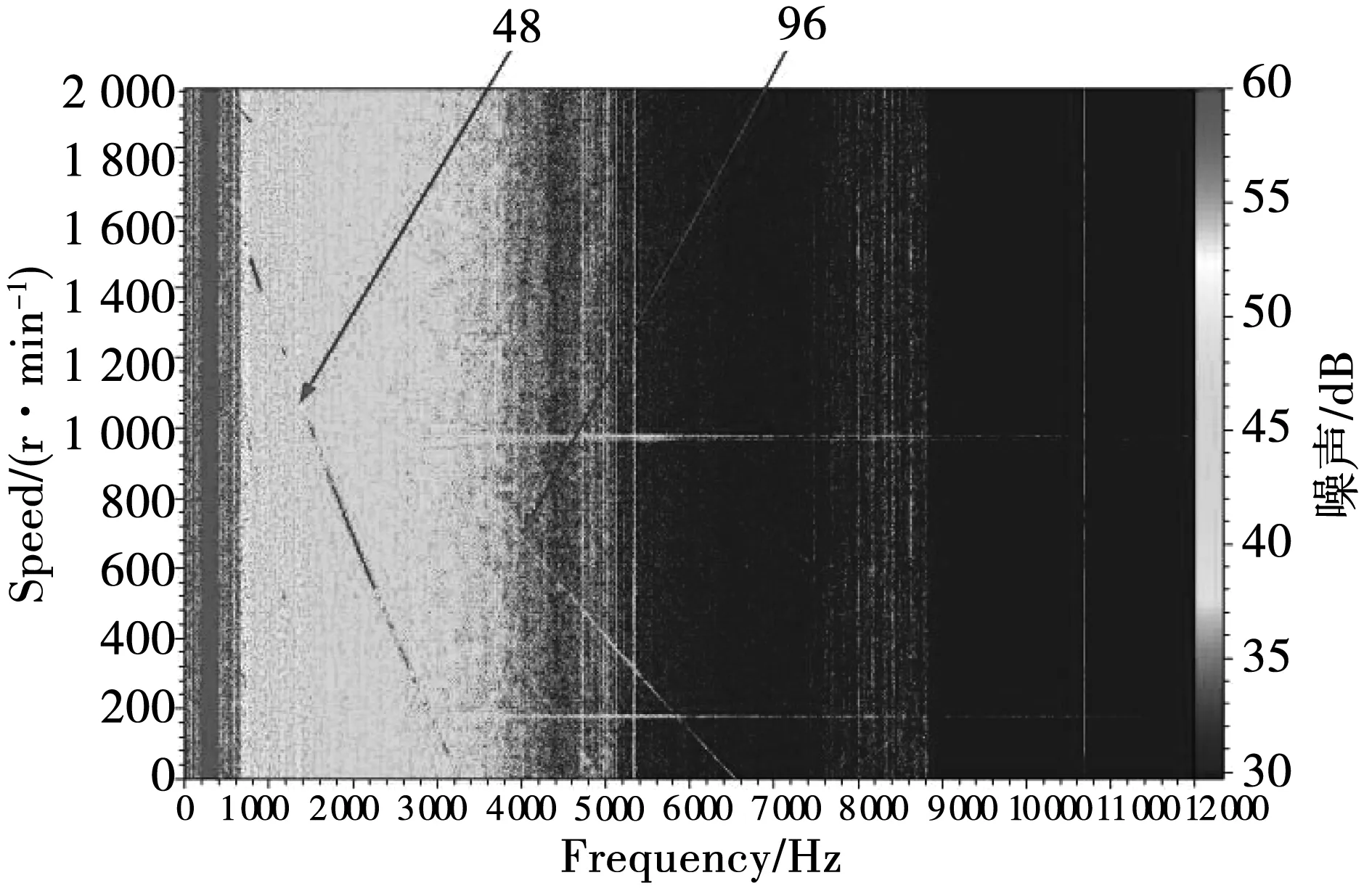
图11 空载噪声瀑布图Fig.11 Noise waterfall drawing under no load

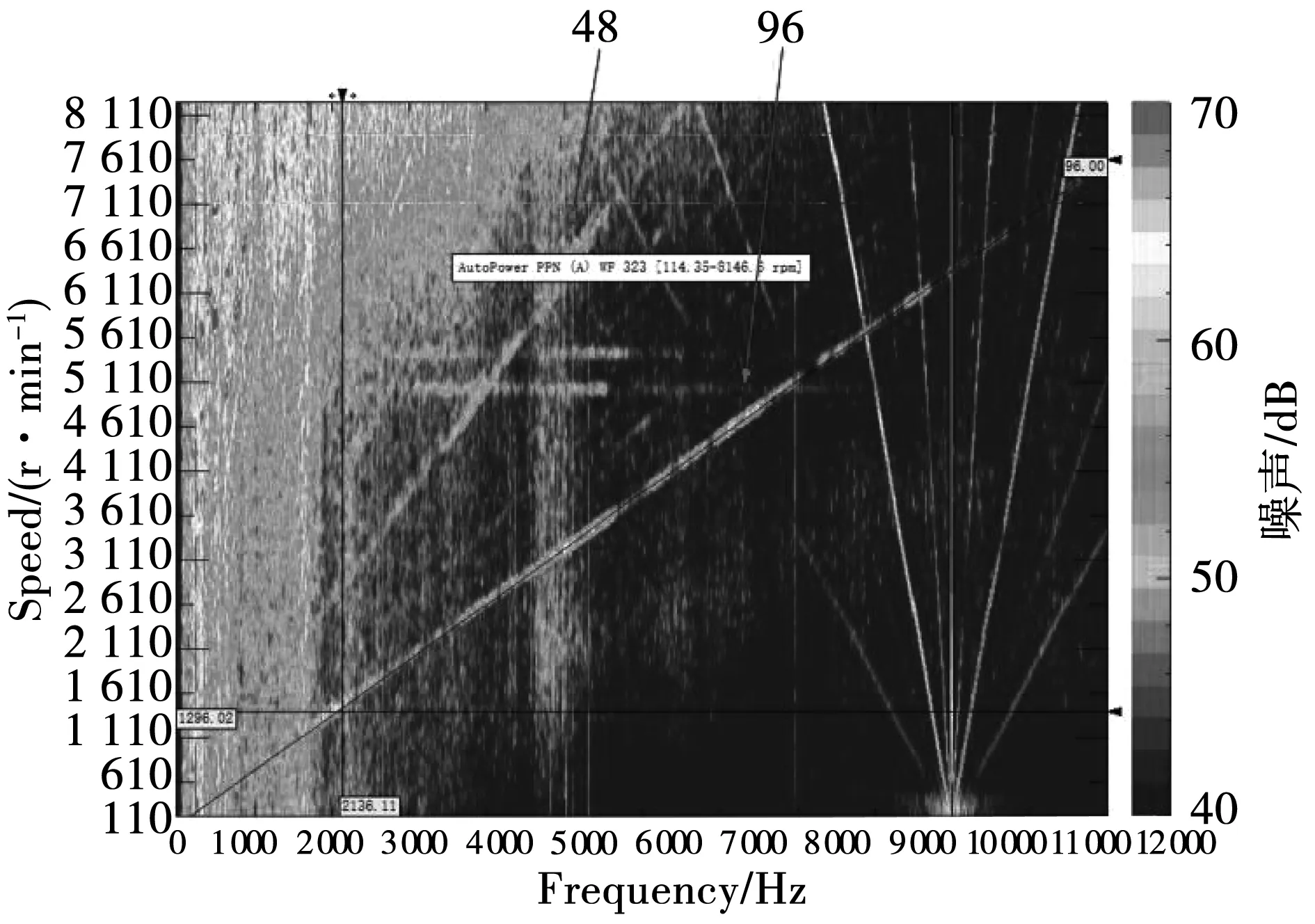
图12 负载20 N·m全转速噪声瀑布图Fig.12 Full speed noise waterfall at load 20 N·m

由图12的实测结果可见，由于采用转子分段斜极和转子表面开辅助槽对一阶和二阶齿谐波引起的噪声的削弱很明显，高速区下的48倍频电磁噪声最大值由80 dB下降到58 dB，考虑到仿真结果偏大的因素，实际的削弱效果并没有这么好，但是，仍然可以看出所提方法对于削弱由一阶齿谐波引起的0阶12f1电磁力波产生的48倍频电磁噪声的有效性。而96倍频的噪声在定子铁心0阶固有频率7 235.9 Hz附近产生较大噪音，噪声最大值为63 dB。

4 结 论

本文对一款车用内置式永磁同步电机转子结构优化降低电机电磁噪声的机理展开研究。仿真和实验结果表明：低阶齿谐波引起的0阶电磁力在接近电机定子0阶固有频率时会达到共振条件激发幅值大的噪音，采用转子分段斜极能有效的削弱在高转速区时由齿谐波引起的0阶12f1电磁力产生的48倍频电磁噪声，结合转子表面开辅助槽后削弱效果更好。