高速永磁同步电机流固耦合仿真与性能分析

丁树业，申淑锋，杨智，陈少先，戴瑶

(1.南京师范大学 南瑞电气与自动化学院，南京 210023；2.中国船舶重工集团公司第七〇四研究所，上海 200031)

0 引 言

高速永磁同步电机(high speed permanent magnet synchronous motor, HSPMSM)，因其具有效率高、功率密度大，以及可直接与高速负载相连接等优点，被广泛的应用于船舶驱动、风力发电、矿用电机等场所[1-4]。与普通电机相比，相同功率的HSPMSM的损耗密度更大，且因其具有结构紧凑和散热面积小等特点，电机在运行中易面临温升过高的难题。作为舰船电推进系统，考虑到过高的温升将造成永磁体不可逆退磁[5-6]，对船体安全运行造成严重威胁，因此对HSPMSM进行温度场研究以及冷却系统优化具有一定的研究价值和实际意义。

由于计算机性能的提高以及数值计算方法的发展，国内外学者多采用数值模拟方法对HSPMSM温度场与流体场进行研究。董宝田等学者提出了一种磁热液耦合迭代的多物理场方法，对一台30 kW的高速永磁电机进行仿真计算和实验，验证了该方法的准确性[7]。朱高嘉等学者以一台1.65 MW永磁风力发电机为例，提出转子幅板支架作为离心式风扇的设计思路，并通过数值计算证实其可行性[8]。韩力等学者采用计算流体力学的方法对10 MW空冷高速感应电机内部流场与温度场进行研究，通过在定子铁心背部增加挡风板等结构，改善电机内冷却空气流通路径及分布特性[9-10]。范兴纲等人以一台1.6 MW永磁风力发电机为例，提出了一种具有径向孔的新型通风设计方法，并通过建立3D流固耦合模型验证其有效性[11]。孙明灿等学者对于一台7 kW，4 000 r/min非晶合金轴向磁通永磁电机的涡流损耗进行计算，并对比在定子连接板上安设水道和电机端部安设水套两种冷却方案对温升分布规律的影响，通过对样机温升试验的结果与仿真实验数据进行对比，验证了有限体积法求解电机温度场的准确性[12-13]。文献[14]以20 kW车用永磁同步电机为例，通过流固耦合计算，对比不同水道结构及水道入口流速下电机温升分布规律，确定最优水冷方案。文献[15]为探讨风速和散热面积对电机温升的影响，以一台100 kW混合励磁发电机为例进行研究，考虑到电机结构对称性，建立了1/10求解区域进行分析计算，得到电机风速和散热面积与电机温升的倍比关系。以上大部分的研究者都是以高速电机整体模型的一部分作为建模对象，当电机采用非全域建模时，需要结合电机结构进行简化，而全域建模能够克服简化过程对计算结果带来的误差，提升计算结果的精确度。

本文以一台空冷、水冷结合冷却的200 kW现代舰船高速永磁同步电机为例，结合电机实际结构搭建三维整机求解域模型。在流体动力学及流固耦合传热理论基础上，给定基本假设与边界条件，采用有限体积法进行求解，首先分析螺旋型水道入口水速对电机温升的影响，揭示出最优水速方案下电机流体流动特性与各部件温升分布规律。在此基础上，提出一种轴向通风方案，在入口风量不变的前提下，强迫空气通过气隙进行轴向通风，对比优化前后电机内流体场与温度场计算结果，证实该结构能够改善电机的冷却性能，本研究为HSPMSM在冷却系统设计方面提供一定的借鉴意义。

1 求解模型确立

1.1 电机基本参数

研究对象为一台200 kW船用高速永磁同步电机，其基本参数见表1。

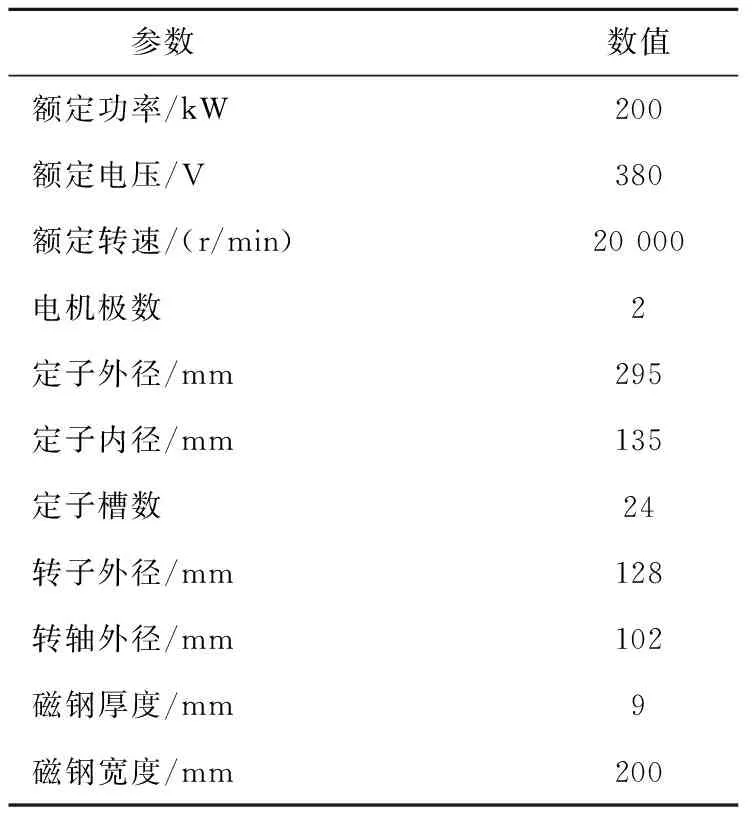
表1 200 kW高速永磁同步电机基本参数

图1为样机实物图，根据电机参数与冷却结构建立的电机三维全域物理模型如图2所示。由图可知该电机采用空、水冷结合冷却，机壳设置两组通风入口，冷却空气自入风口流入，大部分聚集于电机两侧端腔，带走端腔内热量再从对应出风口流出。由于定转子之间气隙狭窄，只有少部分空气流入气隙，沿轴向进行冷却。铁心段内热量沿径向传导至机壳，被嵌设在机壳内的螺旋型冷却水道吸收。

图1 样机实物Fig.1 Motor prototype

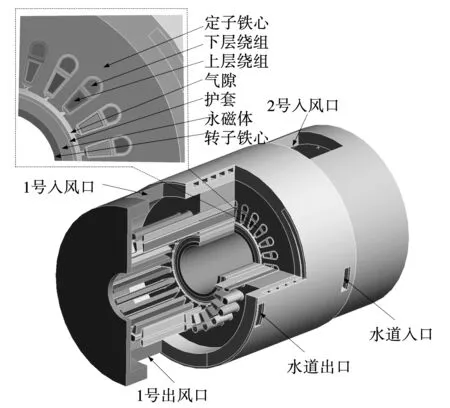
图2 电机物理模型Fig.2 Physical model

1.2 数学模型

对电机额定运行状态下的温度场进行计算，该电机定子铁心由DW250-35硅钢片叠制而成，护套采用碳纤维材料，二者导热系数设定时需考虑介质的各向异性。由于电机冷却系统采用空冷、水冷结合冷却，因此热量传递主要以热传导和热对流形式发生，不考虑辐射换热的传递方式。基于如上前提，电机内部三维导热控制方程在笛卡尔坐标系中可以表示[16-17]为：

(1)

式中：λx、λy、λz分别为不同材料沿x、y、z轴方向的导热系数，W/(m·K)；T为待求温度，K；qv为电机内的总热源值，W/m3；S1为绝热面；S2为散热面；α为表面散热系数，W/(m2·K)；Tf为电机的环境温度，K。

电机内冷却介质的流动会受到质量、动量及能量守恒定律的约束。当电机内部流体为不可压缩，并且处于稳定流动时，相应流体通用的控制方程式[18]为

div(ρuφ)=div(Γgradφ)+S。

(2)

式中：φ为通用变量；ρ为流体密度，kg/m3；Γ为广义扩散系数；S为源项。

1.3 基本假设

为合理简化流固耦合的计算过程，对求解模型作如下基本假设[16-18]：

1)电机内冷却介质马赫数较小，将流体视为不可压缩流体；

2)鉴于电机内流体雷诺数较大，故采用湍流模型对流体场进行求解；

3)不计浮力及重力对电机内流体的影响；

4)忽略铁心叠片之间的接触热阻，认为电机各部分绝缘良好。

1.4 边界条件

根据电机额定状态下的稳定运行性能，结合其冷却结构特点，给定边界条件如下：

1)风路入口采用速度入口边界条件，两入风口流速均设置为3 m/s；冷却空气出口定义标准压力出口，环境温度设置300 K。

2)螺旋形水道定义为速度入口，水道出口与冷却空气出口边界条件保持一致。

3)根据电机额定运行时的工况，转子外壁面设为旋转壁面，转速给定20 000 r/min。

1.5 热生成率确定

基于有限元法对电机电磁损耗进行仿真，依据经验公式计算机械损耗从而确定求解模型主要部件的损耗数值。在热仿真分析中，损耗通过单位体积的热生成率进行施加[19-22]，电机内所有产热部件的热生成率详情如表2所示。

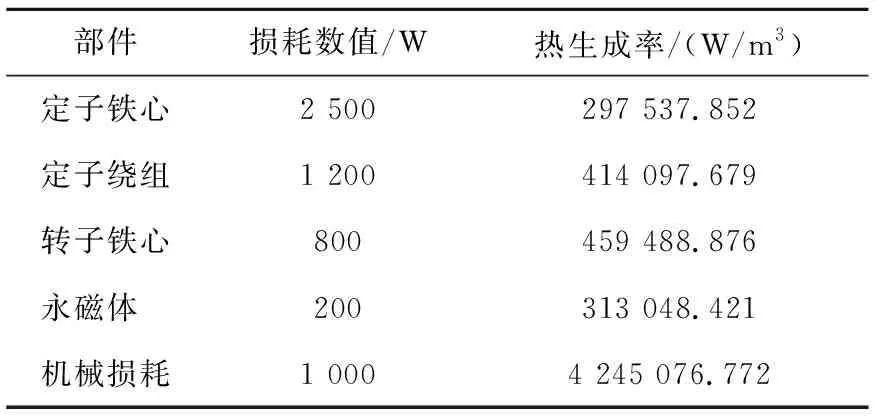
表2 电机内损耗分布与热生成率

2 数值求解计算

2.1 水冷方案确定

基于上述基本假设与边界条件，图3展示出不同入口水速方案下永磁体和定子铁心的最高温升。当入口水速小于0.4 m/s时，永磁体与定子铁心温升随水速提高，呈现下降趋势；当水速超0.4 m/s之后，永磁体与定子铁心两者温升趋于稳定状态，水速从0.4 m/s升至1 m/s过程中，二者温升变化幅度均不超过1 K。因此，选定最优水速为0.4 m/s，该方案下的永磁体与定子铁心温升相较于水速为0时的纯空冷方案分别降低了21.14 K和29.12 K，占各自纯空冷方案下温升的比例分别为14.06%和37.67%，由此可以看出水速提升对定子铁心温升影响较大，而永磁体受水冷的影响有限。

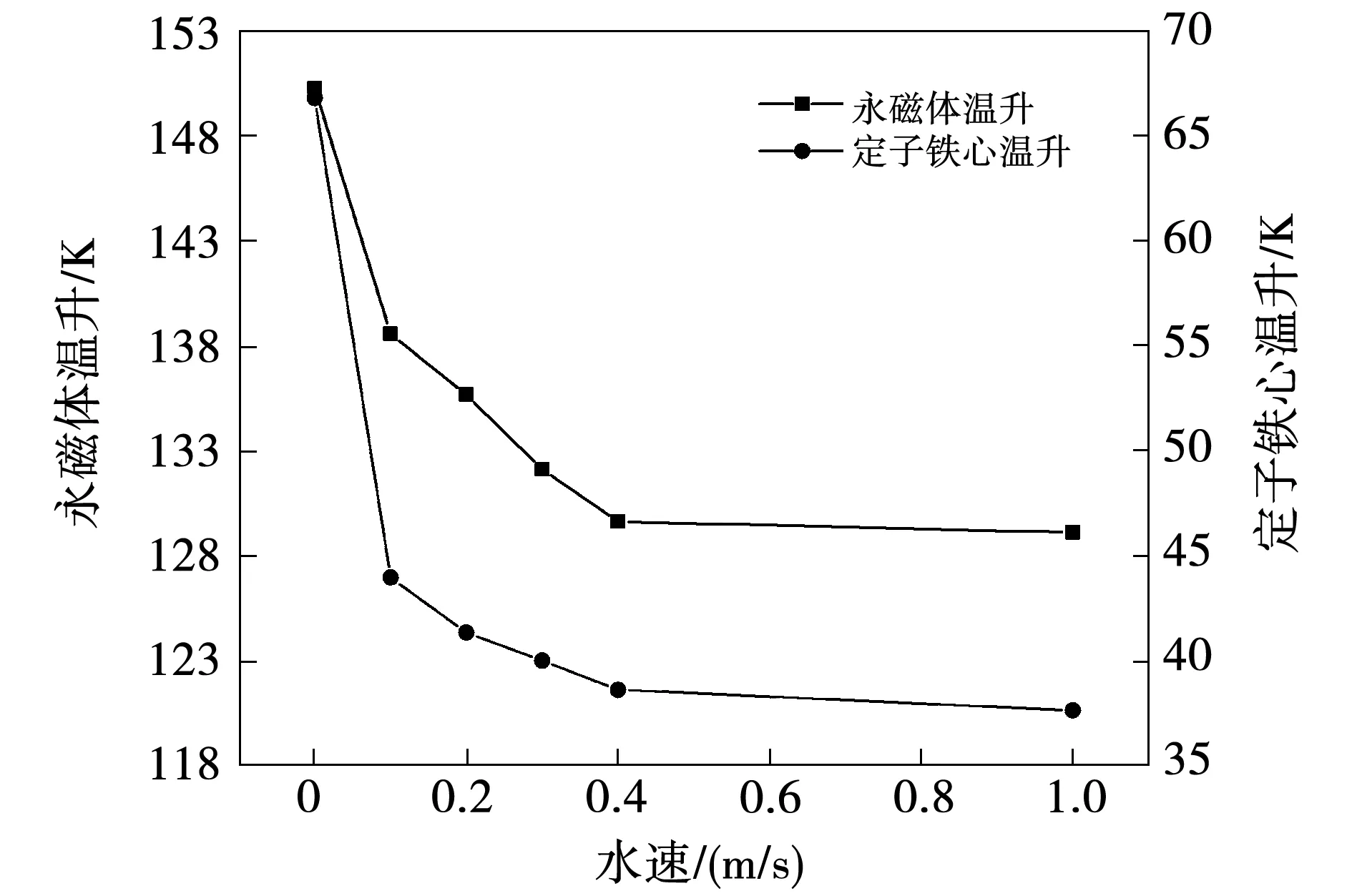
图3 不同水速下的温升Fig.3 Temperature rise at different water velocity

2.2 流体场分析

根据2.1节内容确定的最优水速方案，在数值求求解过程中将水道入口速度设为0.4 m/s，进而对电机进行流温耦合数值计算。图4为电机内冷却空气迹线，电机内部冷却空气分布呈现对称性，气隙内空气受到转子带动作用流速较高，由于气隙内冷却空气对向流动，轴向中心位置风量几乎为0。两侧端部风路宽阔，冷却气体流量大但是流速较低，左端平均速度为1.71 m/s，右端平均速度为1.54 m/s。

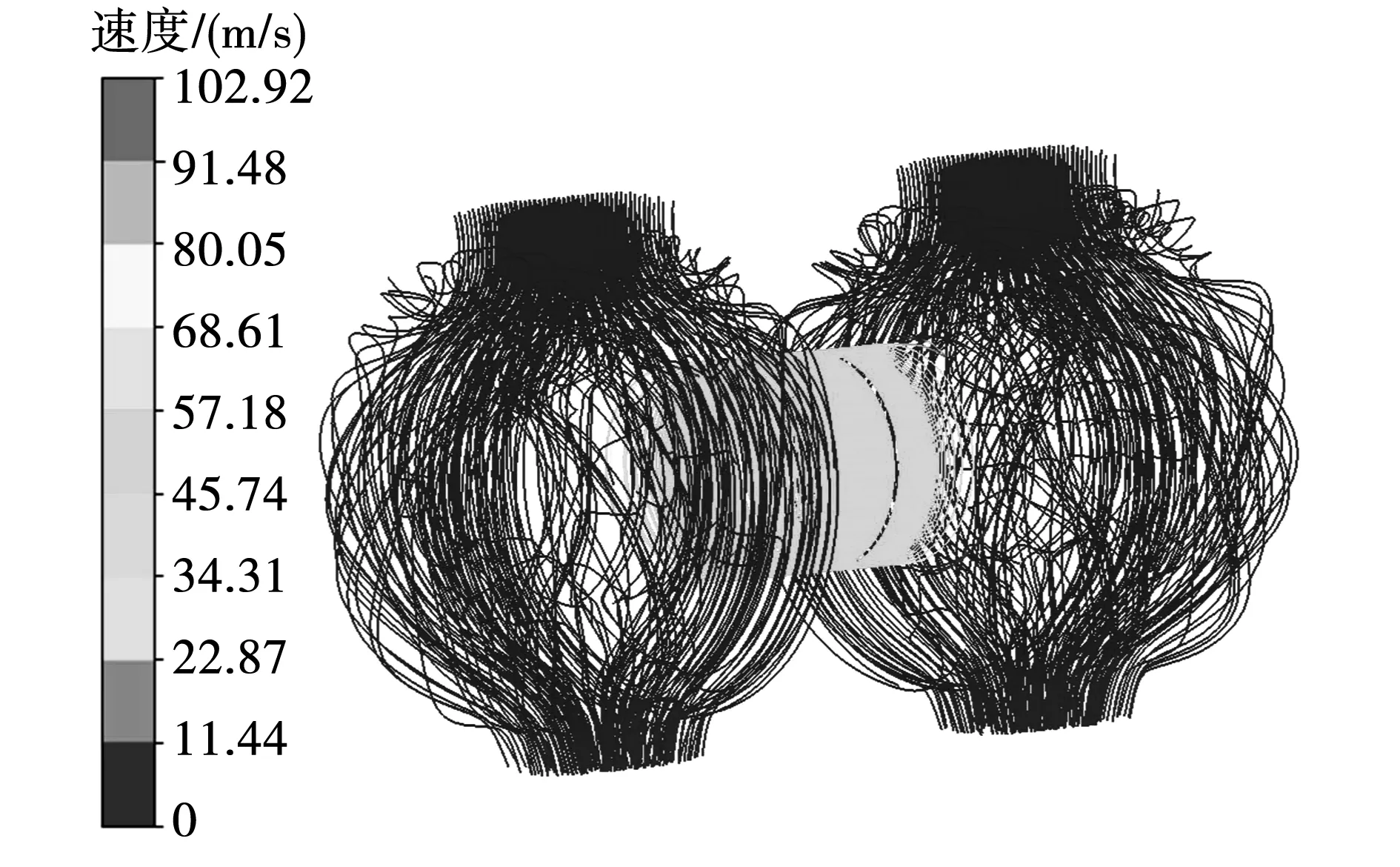
图4 冷却空气迹线Fig.4 Cooling air trace map

图5给出流体域轴向截面速度分布情况，由图可知两侧端腔内流体速度很低，与迹线分布一致。由于转子外表面设置为高速旋转的运动边界，贴近转子侧的气隙区域会出现负压，当空气在刚进入气隙时受风路挤压作用，流速会突然增加，因此最高流速为102.92 m/s，出现在气隙两端贴近转子侧区域，气隙内平均流速为61.49 m/s。

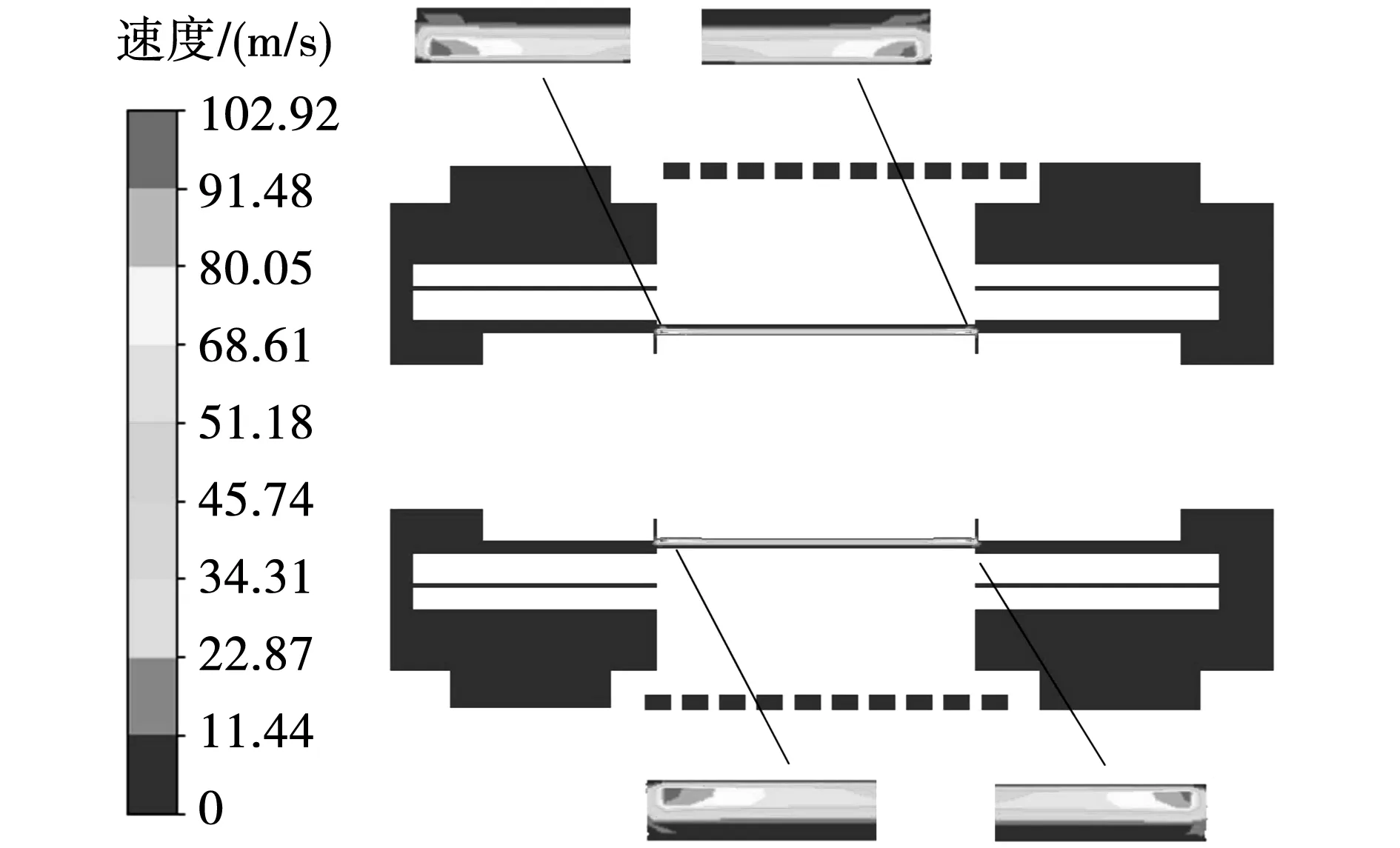
图5 流体场轴向速度分布Fig.5 Axial velocity distribution of fluid field

机壳外侧水道流体场计算结果如图6和图7所示，冷却水在水道壁面的约束下，呈螺旋流动状态。由图6可知，冷却水在流通过程中受到液体流动的趋肤效应影响，最高流速达到2.26 m/s，为入口水速的5.65倍。图7为水道内部压强分布图，水道内流体压强最大值出现在入水口过渡区，最大压强为41 614 Pa。压强最低值出现在水道出口段，由于水道边界为速度入口与压力出口，液体在迅速流动的过程中，会有静压为负的情况出现，水道进出口压差为41 730 Pa。

图6 水道速度分布Fig.6 Streamlines in water channel

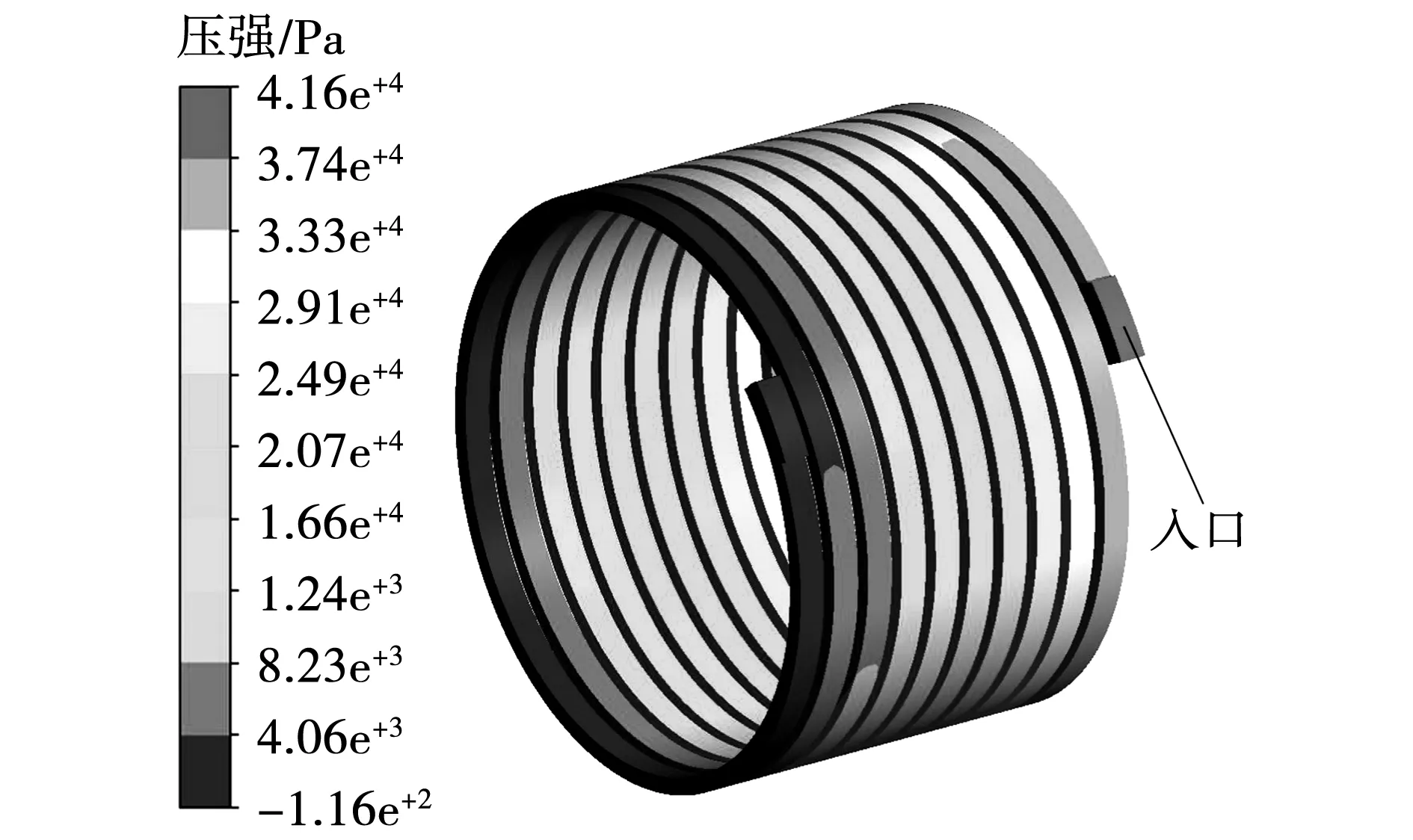
图7 水道压强分布Fig.7 Pressure distribution in water channel

2.3 流体场分析

电机在运行过程中各部件产生的损耗将通过与冷却介质进行热量交换的方式进行散热[23]。通过仿真软件进行计算，电机在额定工况下的温升详情如图8～图11所示。结合图8与图11可知，由于受到水冷和风冷综合冷却的影响，定子铁心温升在轴向上分布不对称。冷却液沿螺旋型水道流动过程中，吸收机壳热量，水温逐步升高，而定子轭部靠近机壳，受水冷影响较为明显，在靠近水道入口侧温升较低。由于作为热源的绕组缠在定子齿上，使得齿部散热困难，且电机内的热量沿着径向传递，转子部分产生的热量通过气隙向机壳进行传递，因此铁心内侧温升较高，最高温升为43.79 K，出现在定子铁心内侧的轴向中心位置。根据流体场计算结果可知气隙内空间狭窄，风量远小于两侧端腔，铁心段内绕组被绝缘包裹，端部绕组能与冷却气体进行充分换热，因此图9中的定子绕组最低温升出现在靠近入风口侧的端部位置，最高温升为32.05 K，出现在上层绕组的轴向中心位置。为降低电机涡流损耗，护套采用碳纤维材料，但其导热性能较差，为永磁体散热带来较大困难，根据图10可知永磁体上温升最高值为130.57 K，出现在轴向中心处。

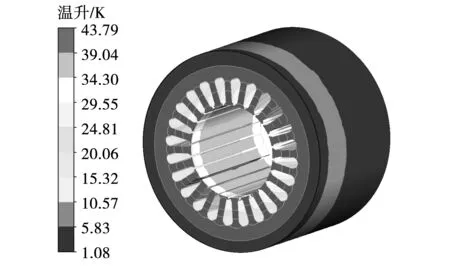
图8 定子铁心温升Fig.8 Temperature rise distribution of stator core

图9 定子股线温升Fig.9 Temperature rise distribution of stator winding

图10 永磁体温升Fig.10 Temperature rise distribution of permanent magnets

图11 水道温升Fig.11 Temperature rise distribution of water channel

3 不同通风方案冷却性能分析

3.1 方案概述

电机永磁体采用N38UH钕铁硼材料，该材料极限工作温度为180℃，通过换算可知其允许最高温升为153.15 K，而原始空、水冷冷却方案下永磁体最高温升达到130.57 K，其冷却效果仍有改进空间。通过对永磁同步电机原始方案流体场进行分析可知，两端腔内仅少量冷却空气沿气隙流向中心位置，空气对向流动将造成能量损失和冷却能力的降低，因此电机需增设水冷系统进行二次冷却。根据2.1节内容可知，通过提升水冷系统入口水速对于冷却电机转子带来的效果是有限的，而气隙与转子外表面直接接触，通过空气流动带走热量是转子散热的主要方式。因此对于降低永磁体温升应从消除气隙内对向流动，提升气隙处散热能力入手。

基于上述，提出一种轴向通风结构，在保持总风量不变的前提下，将1号入风口和2号出风口进行封堵，2号入风口速度设置为6 m/s，迫使冷却空气沿狭窄气隙流动进而形成轴向通风道，提升气隙散热能力，从而达到降低电机温升的目的。为单独分析通风结构对电机散热能力的提升效果，将入口水速设置为0，该边界条件设置下的计算结果能够更直观反映通风结构对电机的冷却效果。

3.2 不同方案仿真结果对比

保持前文基本假设以及相同求解域的前提下，对双端入风与轴向通风两种通风结构的电机分别进行仿真运算，表3给出了双端入风与轴向通风方案下各部件最高温升数据对比。由表可知该电机采用轴向通风方式后最高温升相较双端入风方案下降40.02%，各部件温升均得到改善。

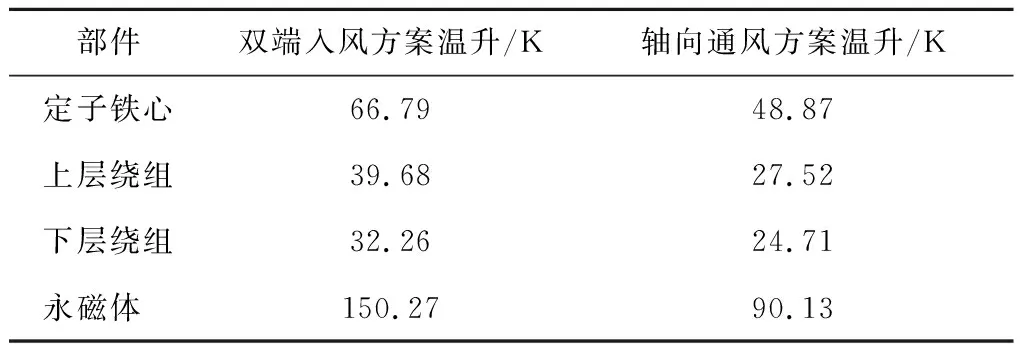
表3 不同方案中各部件最高温升对比

图12所示为两种方案下电机内流体迹线，图13为两方案中不同流域的平均流速对比。结合图片可知，轴向通风方案中各区域流体流速均高于双端入风方案，轴向通风结构避免了原始方案中空气对向流动造成气隙轴向中心位置流量为零的情况，气隙最高流速为146.95 m/s，为原始方案的1.51倍；左、右端部的平均速度分别提高了8.99 m/s和0.76 m/s，轴向通风结构有效提升了流体域整体的平均流速，改善了电机内部流场分布特性，从而利于电机内热源部件的散热。

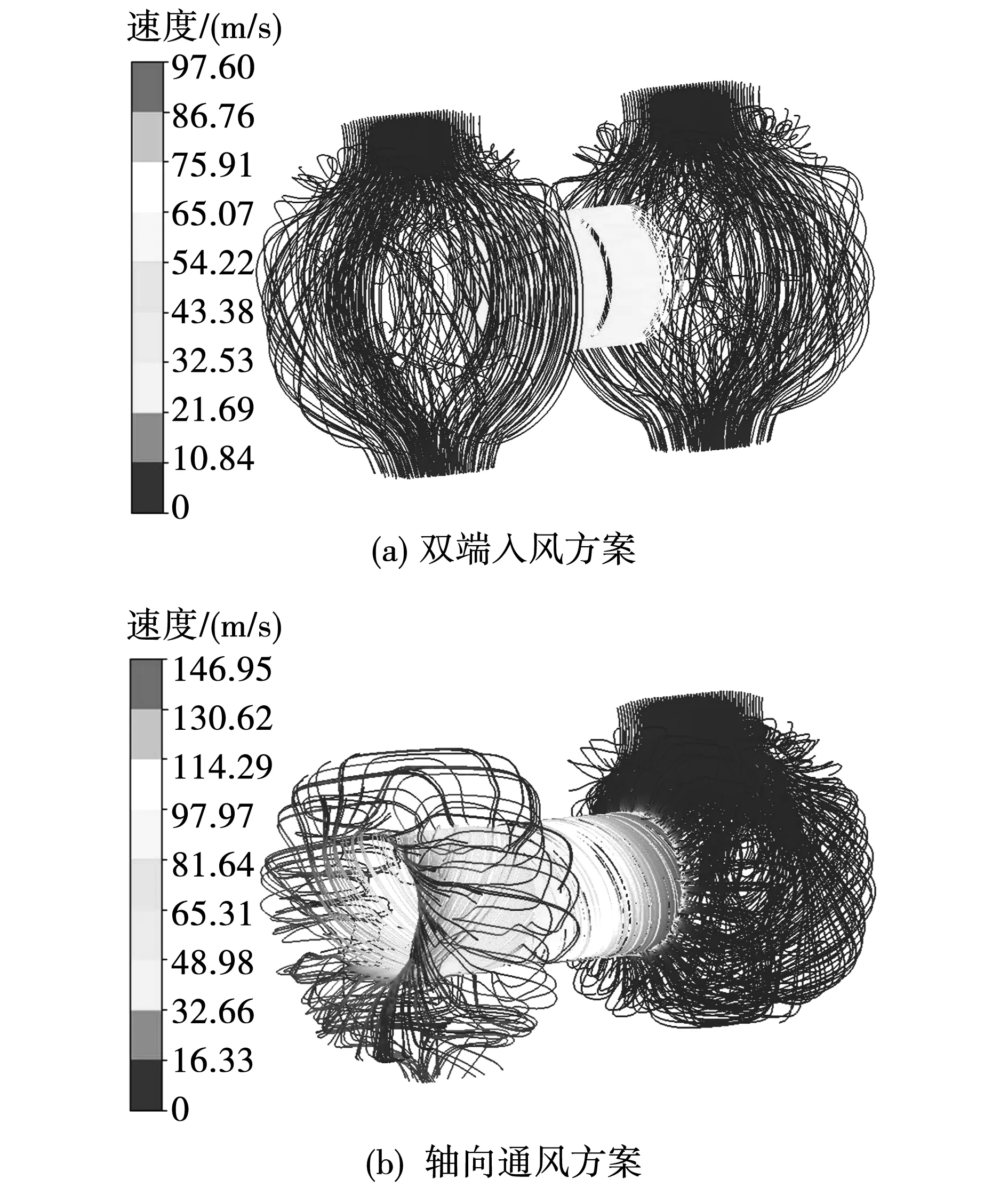
图12 不同方案中冷却空气迹线Fig.12 Cooling air trace map

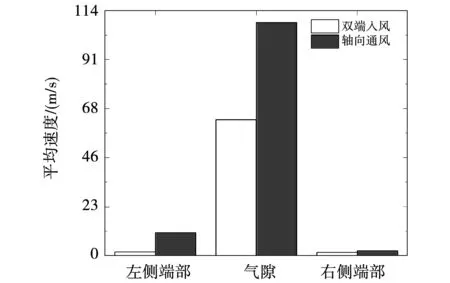
图13 不同方案中流体流速分布Fig.13 Fluid velocity distribution

图14为两种方案下电机轴向截面的温升分布，如图14(a)所示，在双端入风方案中，电机温升分布关于轴中心对称，靠近入风口处温升较低；轴向上两端气体冷却效果好，端部温升低于中心位置。由图14(b)可以看出轴向通风方案使得电机各部件温升均得到降低，最高温升降低了60.28 K；轴向上，冷却空气在沿轴向风路流动过程中，将热量一并带走，左端靠近出风口侧温升高于右端。图15为两种方案下电机轴向中心截面沿径向温升分布，转子部分温升高于定子，且轴向通风结构对转子散热性能改善显著。

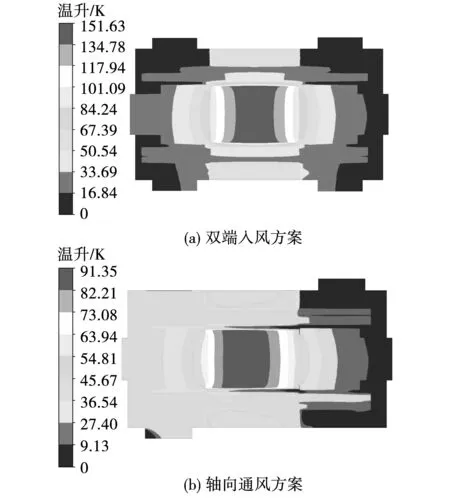
图14 不同方案中电机轴向截面温升分布Fig.14 Cooling air trace map

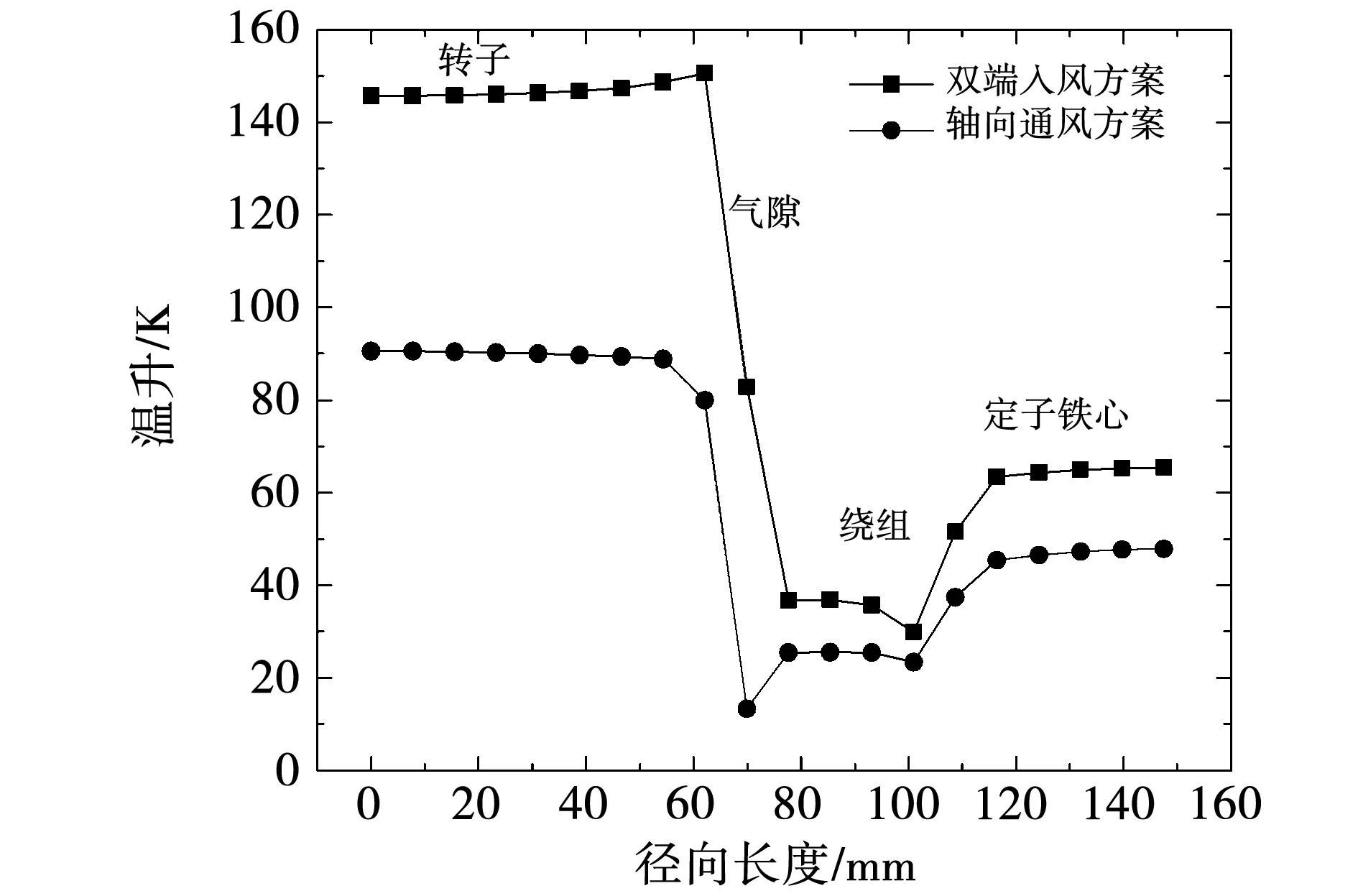
图15 不同方案中轴向中心面的径向温升分布Fig.15 Radial temperature rise distribution

根据定子铁心与永磁体所在轴向区域等设置等距采样面，提取各采样面的平均温升如图16所示。采用双端入风方式的电机结构具有对称性，因此电机内部温升最高位于轴向中心面上，温升基本沿轴向对称。而轴向通风结构迫使冷却气体沿气隙轴向通风，入风口设在电机右端，冷却气体在沿风路自右向左流通过程中与发热部件进行热交换，电机温升最高位置向左偏移20 mm，且定子铁心和永磁体右端温升低于左端。

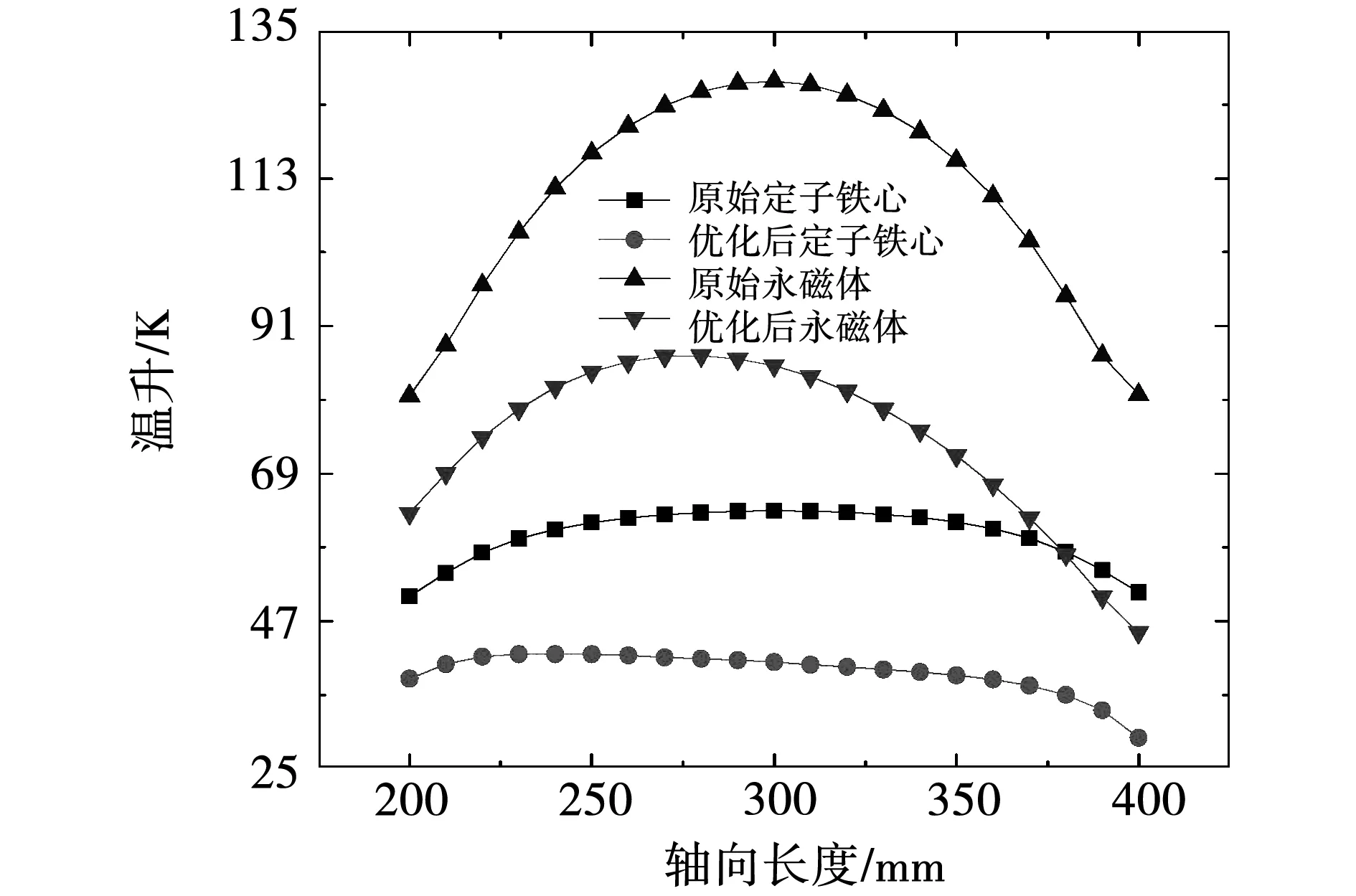
图16 不同方案中轴向中心面的轴向温升分布Fig.16 Axial temperature rise distribution

为更直观研究通风结构对定子绕组温升的影响，从电机靠近1号入风口端部向右看去，电机顶部定子槽命名为1号槽，沿顺时针方向依次进行编号，取24槽内上、下层绕组平均温升如图17 (a)所示，由图可知轴向通风方案相较于双端入风方案的上、下层绕组平均温升分别降低6.58 K和3.29 K；双端入风方案上、下层绕组在周向上温升波动差值分别为4.5 K和6 K，轴向通风方案中24槽内上、下层绕组沿周向温升差值分别降低至1.9 K和3.8 K，由此可见轴向通风结构使绕组在周向上温升整体降低且分布更为均匀。图17 (b)为两种方案中定子绕组在轴向上的温升，可以看出在双端入风方案中，定子绕组温升分布关于轴中心对称，上、下层绕组沿轴向的温升波动差值分别为15.9 K和14.4 K，上层绕组温升高于下层绕组，这主要是由于电机转子部分热生成率高，气隙宽度仅为3.5 mm，铁心段内绕组散热能力有限，而端部绕组可以与大量冷却空气直接接触，冷却效果更优，因此端部绕组温升低。轴向通风方案中，绕组在右侧端部以及气隙所在轴向段内温升均低于双端入风方案，上层绕组温升同样高于下层绕组。由于轴向通风结构会导致左侧端部空气温度上升，因此在靠出风口侧绕组冷却效果不及双端入风方案，但是总体而言，采用轴向通风结构之后，上、下层绕组轴向最高温升相较双端入风结构分别下降了11.5 K和6.6 K，上层绕组靠近气隙，而轴向通风结构提高了气隙的流动速度和冷却能力，因此上层绕组温升下降幅度高于下层绕组。

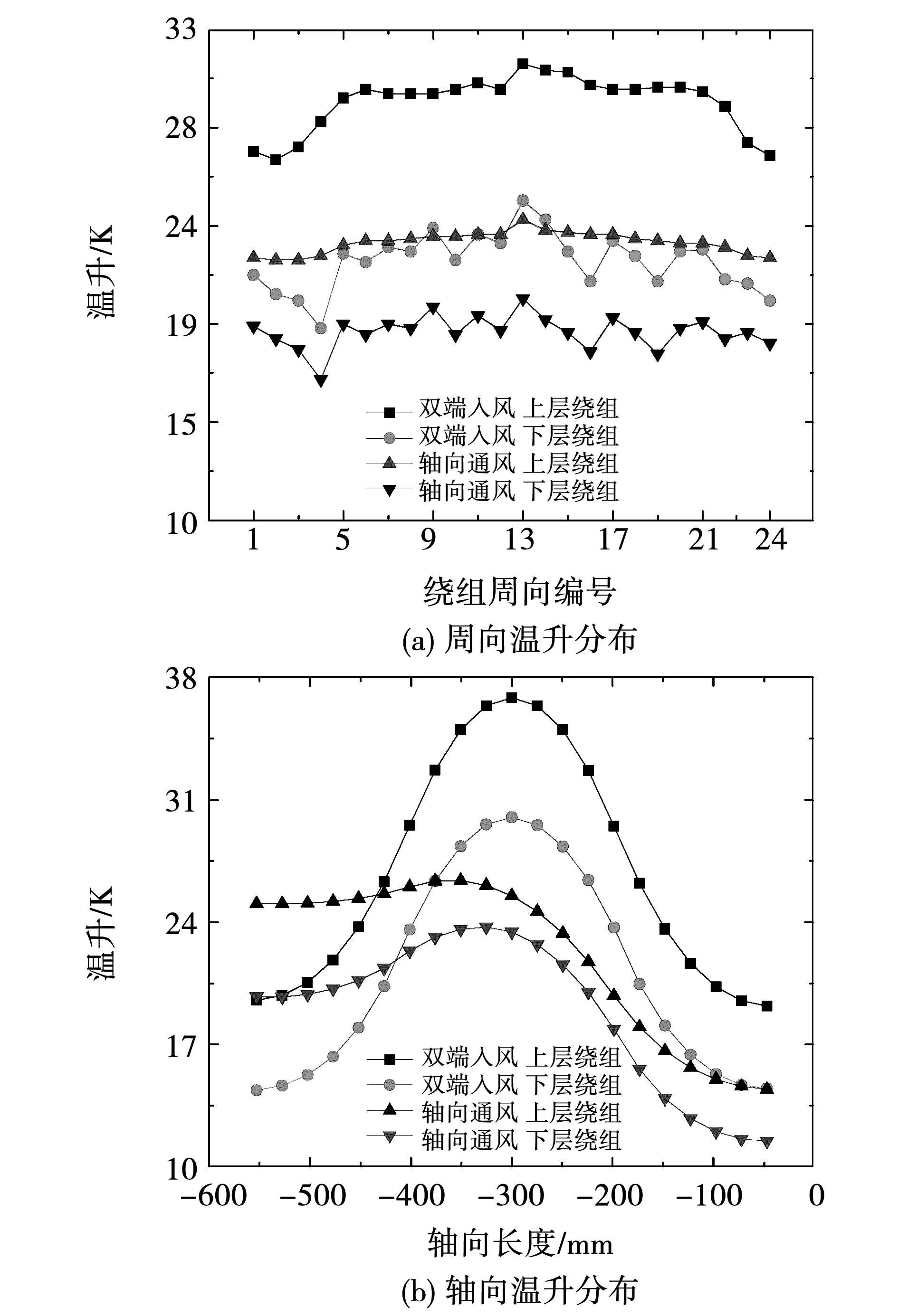
图17 定子绕组温升分布Fig.17 Temperature rise distribution of winding

4 实验验证

为验证前文分析方法的准确性，对200 kW高速永磁电机进行温升试验，并对试验工况下的电机温升进行数值求解。图18所示为电机温升试验平台，该电机在17 000 r/min工况下进行测试，实验中在永磁体表面放置温度传感器来测量温度。环境温度为33 ℃情况下，电机保持稳定运行时传感器最高温度为104 ℃，数值仿真结果中传感器位置处永磁体温升为73.28 ℃，温升误差为3.21%，证实了用数值仿真方法模拟电机温升的可行性，间接佐证了前文分析结果的准确性。

图18 温升试验平台Fig.18 Temperature rise test device

5 结 论

本文以一台200 kW高速永磁同步电机为例，通过建立三维整机求解模型，基于流体动力学及流固耦合传热理论，采用有限体积法对电机模型进行数值求解运算，得出如下结论：

1)入口水速对电机温升的影响是非线性的，水冷系统可充分带走定子部分热量，对转子冷却效果有限。

2)最优水速方案下电机两侧端腔内涡流较多，轴向中心位置流量几乎为0；转子温升高于定子，最高温升出现在永磁体上。

3)在总风量不变的前提下，采用轴向通风结构对电机内部流场分布有改善效果，气隙最高流速提高为双端入风方案的1.51倍。

4)采用轴向通风结构令电机各部件温升均得到下降，定子绕组在周向上的温升分布更为均匀，上层绕组温升下降幅度高于下层绕组。