表贴式永磁同步电机改进滑模观测器控制

吕德刚，李子豪

(哈尔滨理工大学 大型电机电气与传热技术国家地方联合工程研究中心，哈尔滨150080)

0 引 言

永磁同步电机具有结构简单，响应速度快，可靠性高，质量轻及功率因数高等优点，适用于稳态精度需求较高、调速范围需求较大的场合[1-5]。永磁同步电机转轴上安装机械传感器易受环境影响，降低其稳定性，并且增加电机成本。针对上述问题提出采用无位置传感器技术替代机械有位置传感器的改进方法[6]。目前滑模变结构控制方法被广泛应用于各种中高速无传感器控制系统中[7]。

文献[8]采用传统滑模观测器，通过观测电机的相电压和相电流估算出电机的速度和转子位置角度。由于传统滑模变结构控制会出现抖振，使结果偏离实际值，所以文献[9]提出用连续的饱和切换函数sat(x)代替传统的不连续切换函数sign(x)，重新定义滑模切换函数。文献[10-11]提出用趋近律的方法减小滑模运动中的抖振，通过指数趋近律控制缩短了运动点到达滑模面的运动时间，并降低了运动点到达滑模面时的速度。在滑模观测器后面进行二次低通滤波[12-13]或者采用卡尔曼滤波[14-15]同样可以减小滑模面上出现的抖振问题。近年来新的滑模算法被提出，通过更加复杂的算法也可以减小系统抖振，如采用超螺旋的二阶滑模算法[16-17]。此外文献[18]提出用变积分滑模观测器削弱在线性区造成的电流观测误差并减小抖振。

在向滑模面运动过程中，频繁的开关切换和惯性的存在造成系统的抖振不可避免。为了在上述抑制抖振方法基础上，进一步减小抖振。本文选取在零点处连续的切换函数代替不连续的切换函数并和指数趋近律结合的控制方法，抑制传统滑模观测器出现的系统抖振，并进行仿真和实验研究。

1 永磁同步电机的数学模型

根据永磁同步电机的永磁体在转子上摆放方式的不同，可分为表贴式永磁同步电动机、内嵌式永磁同步电动机和内埋式永磁同步电动机。表贴式永磁同步电动机具有均匀的气隙磁场，其交直轴电感系数近似相同[19-20]，磁阻转矩几乎为0，可近似等效于隐极同步电动机。因此，选取表贴式永磁同步电动机进行分析。假设永磁同步电机定子绕组三相相互对称，磁路近似为线性，转子上阻尼绕组为0，忽略定子铁心的饱和现象，不计涡流和磁滞损耗，构造永磁同步电机在两相静止α-β坐标系下的数学模型。

α-β坐标系下的定子电压方程为：

(1)

式中：uα、uβ为α-β坐标系下电压分量；iα、iβ为α-β坐标系下电流分量；R为定子电阻，L为定子电感；eα、eβ为α-β坐标系下反电动势分量。

反电动势方程为：

(2)

式中：ψf为永磁体磁链；ω为电机电角速度。

电磁转矩方程为

(3)

式中：Te为电磁转矩；pn为电机极对数；ψα、ψβ为α-β坐标系下磁链分量。

机械运动方程为

(4)

式中：J为电机的转动惯量；TL为负载转矩。

2 滑模观测器算法

2.1 传统滑模观测器原理

由式(2)可知，永磁同步电机的反电动势决定了转速和转子位置角，反电动势eα、eβ为正弦波。将永磁同步电机中可以观测到的定子相电流、相电压作为输入量，根据滑模变结构控制原理构造滑模观测器。通过滑模观测器估算出反电动势信息，进而得到所需量：转子位置角度信息与转速信息。

由式(1)可得α-β坐标系下的电流状态方程为：

(5)

根据滑模变结构控制原理定义滑模面为

(6)

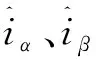
结合滑模观测理论将定子观测电流与定子实际电流做差可得到滑模切换面s(x)。选取常数切换的开关切换法则作为滑模控制函数为

u(x)=Kssign(x)。

(7)

式中：sign(x)为数学符号函数，在x大于0处函数值为1，在x小于0处函数值为-1；Ks为滑模增益。

将反电动势eα、eβ用电流误差开关信号函数表示。并结合式(5) ～式(7)最终得到传统滑模电流观测器为：

(8)

(9)

将式(9)和式(5)做差可得电机定子电流估算方程：

(10)

(11)

上述滑模观测器采用的开关控制函数sign(x)在零点处不连续，导致控制系统在时间和空间上均存在滞后现象。此外，系统惯性和测量误差使运动轨迹反复穿越滑模切换面、形成锯齿波，使系统在运行过程中出现抖振现象[21-22]。

2.2 改进滑模观测器算法

针对上述传统滑模观测器出现的抖振问题，作出了如下改进：首先选取在零点处连续的开关控制函数sigmoid(x)替代原有在零点处不连续的函数sign(x)。sigmoid(x)函数表达式为

(12)

曲线如图1所示。

由图1可知sigmoid(x)在零点处函数值为0且在实数域内连续。图中a可以调节sigmoid(x)的陡度，a的值越大sigmoid(x)在零点附近越抖。为了避免控制函数在零点附近函数值变化太快，影响控制效果。选取a=2时较平滑的sigmoid(x)作为新的切换函数。图中Δ为边界厚度，Δ越大减小抖振效果越好，但会降低控制精度。将x=Δ,y=1代入式(12)中，可以解出Δ=3。当-ΔΔ，x<-Δ时sigmoid(x)函数变成sign(x)函数，此时等效为传统滑模控制。

图1 sigmoid函数示意图Fig.1 Schematic diagram of sigmoid function

滑模运动实际上是由趋近运动和滑模运动两个过程所组成。系统的趋近运动可定义为：从任意初始状态到达切换面的运动。考虑到让系统更快速的到达切换面，结合趋近律控制，选取指数趋近律如下

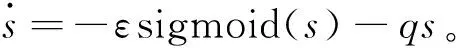
(13)

式中：ε>0,q>0，采用指数趋近律控制，可以减少系统到达切换面的时间，使趋近速度逐渐减少，最终以很小的速度达到滑模面。依然选取式(6)为滑模切换面。

此时电机的反电动势为：

(14)

结合式(5)、式(6)、式(13)、式(14)最终得到改进的滑模观测器算法：

(15)

将式(15)与式(5)作差可得电机的定子电流估算方程：

(16)

为证明滑模运动的可达性、稳定性和存在性。定义李雅普诺夫函数为

(17)

其导数应满足：

(18)

(19)

结合式(16)、式(18)、式(19)可以推得：

(20)

(21)

(22)

(23)

要满足式(18)和式(19)，且ε>0、q>0、R>0，结合式(20)～式(23)可得出

ε>>max{|eα|,|eβ|}。

(24)

通过上述公式推导可知：指数趋近律中的趋近速度ε要远大于反电动势eα和eβ的最大值，才能使滑模运动趋于稳定，并减小抖振。结合上述算法，做出改进滑模观测器的结构示意简图，如图2所示。

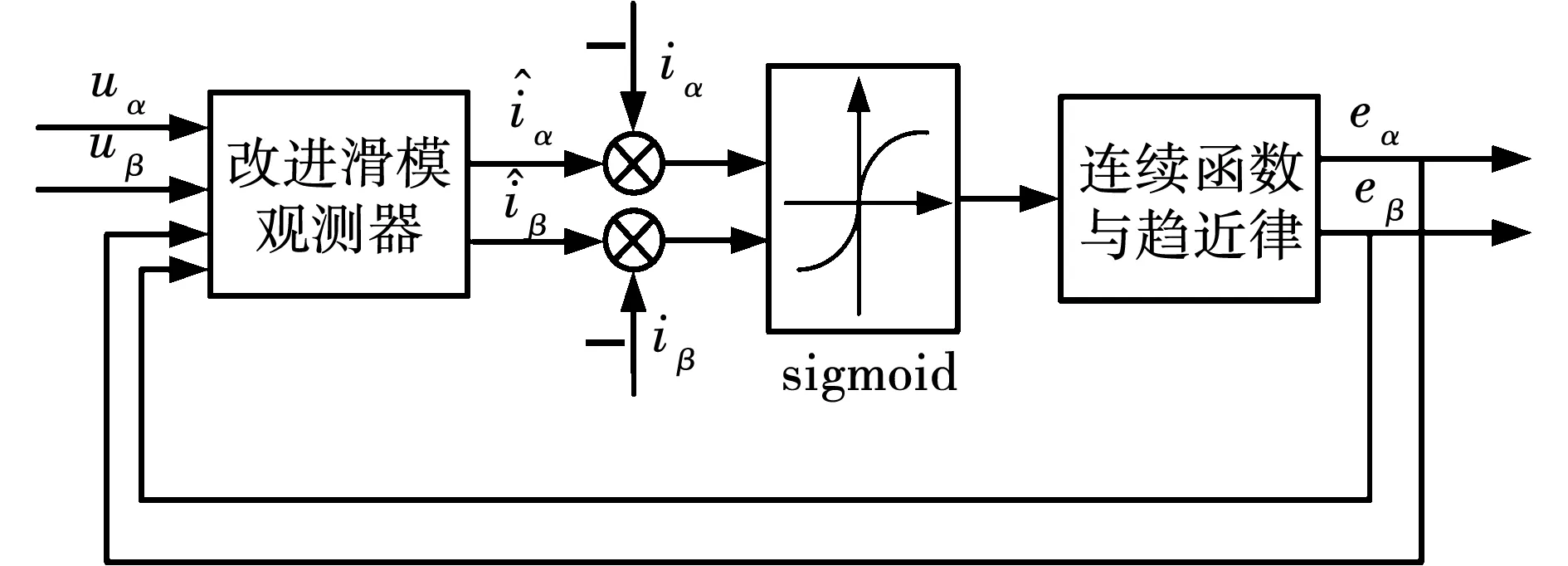
图2 改进滑模观测器结构示意图Fig.2 Structure diagram of improved sliding mode observer

由式(2)及改进滑模观测器算法可推导出永磁同步电机转速和转子位置角度计算公式：

(25)

通过对比恒压频比控制、直接转矩控制、矢量控制的优缺点。最终选取了动态响应高、调速范围较宽的转子磁场定向矢量控制方法，并采用定子直轴电流id=0的控制措施。结合改进后的滑模观测器算法，最终可得出永磁同步电机无传感器控制系统，整体控制系统原理图如图3所示。

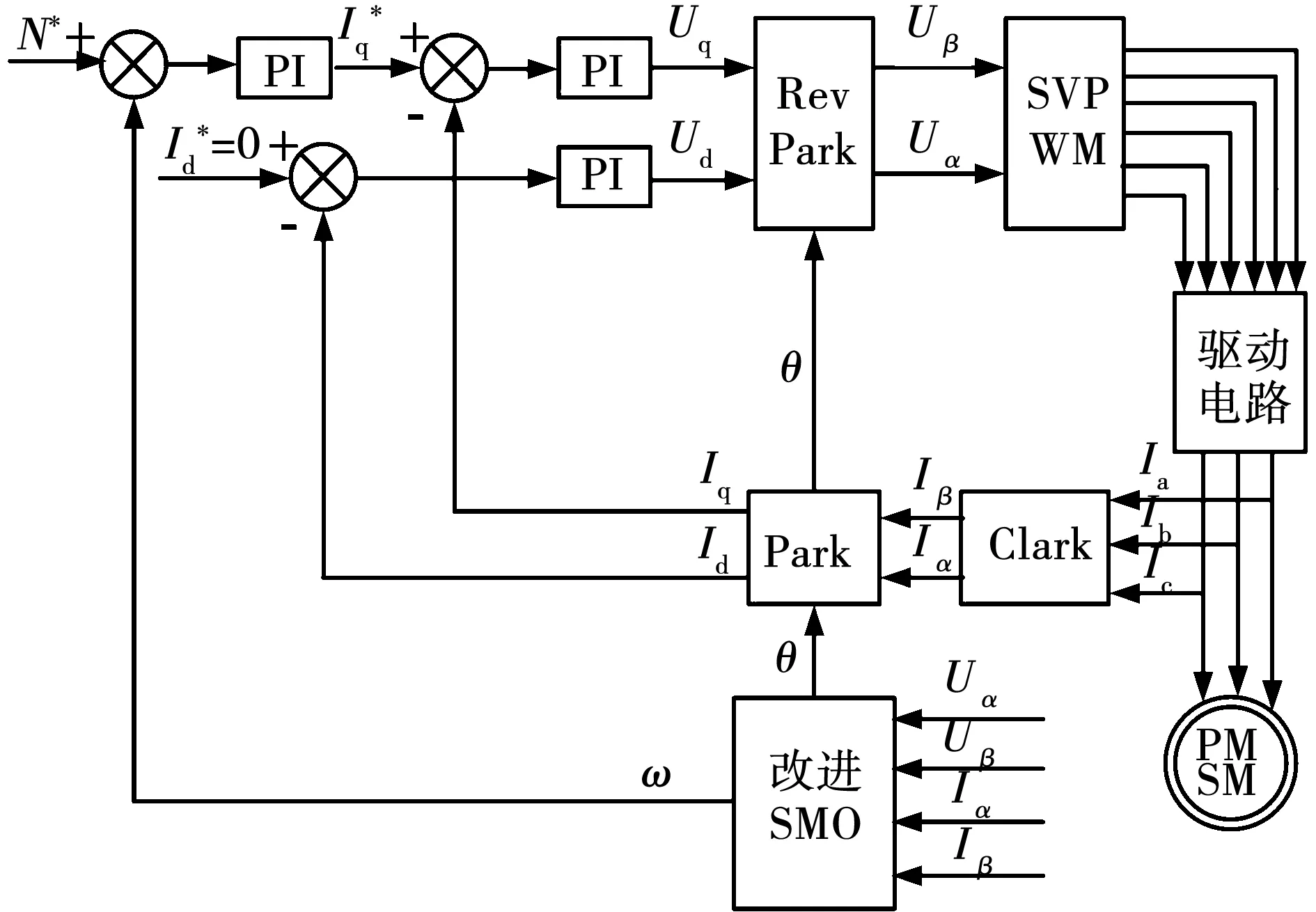
图3 永磁同步电机无传感器控制系统示意图Fig.3 Schematic diagram of sensorless control system of permanent magnet synchronous motor

3 仿真分析

3.1 改进后滑模观测器仿真分析

使用MATLAB软件中的仿真模块系统，对永磁同步电机传统滑模观测器无感控制系统和改进后的滑模观测器无感控制系统，分别进行仿真。

根据所提出的控制方法，采用固定步长2e-7，ode3算法。仿真时间设置为0.1 s，仿真转速设定为1 200 r/min，进行空载实验。MATLAB仿真实验中的仿真模型参数如表1所示。

表1 电机仿真模型的参数

为了更直观反映转子位置角度的估计值和实际值之间的关系。截取了前0.03 s的转子位置跟踪仿真图，转速仿真图截取到0.1 s。传统滑模观测器无感控制系统，仿真实验结果如图4、图5所示。

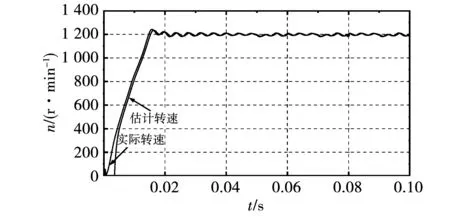
图5 传统滑模观测器转速跟踪图Fig.5 Speed tracking chart of traditional sliding mode observer

由图4可知在前0.002 5 s时，估计的转子位置值较实际值误差较大，因为在电机刚启动的时候转速比较低，在低速区滑模算法不能准确估计转子实际位置。当转速上升时，滑模算法精度变高使转子位置估计值更接近实际值。

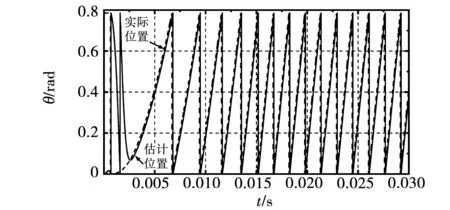
图4 传统滑模观测器转子位置跟踪图Fig.4 Rotor position tracking diagram of traditional sliding mode observer

由图5可知，估计转速在前0.002 s时一直是0，是由于电机刚启动时滑模算法估计不准确。经过大约0.017 s后估计转速达到给定值，但在给定转速1 200 r/min时小幅度波动。其值与给定转速接近，抖振大约在1.7%左右。

改进的滑模观测器控制系统，其转子位置角度仿真同样截取前0.03 s、转速仿真截取前0.1 s。仿真实验结果如图6、图7所示。

由图6可知在前0.001 2 s时，电机刚启动转速较低，滑模算法精度较低，转子位置估计值与实际值误差较大。但相比于传统滑模观测器算法，改进的滑模观测器能更快的减小转子位置估计值与实际值之间的误差。并使估计值更加接近实际值。由图7可知转速依然是先从0上升至给定值，之后稳定在给定转速处。估计的转速大约在0.013 s处达到给定值，与实际值十分接近，在1 200 r/min时波动范围很小，抖振大约在0.8%左右。

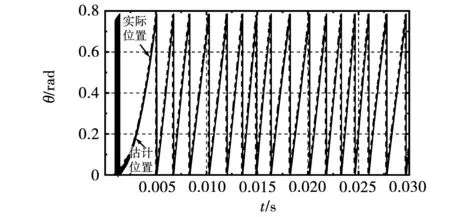
图6 改进滑模观测器转子位置跟踪图Fig.6 Rotor position tracking diagram of improved sliding mode observer

图7 改进滑模观测器转速跟踪图Fig.7 Speed tracking chart of improved sliding mode observer

综上对比传统滑模观测器和改进滑模观测器仿真实验，可以得出：改进后的滑模观测器估计出的转子位置角度和转速值与实际值更加贴近，且能快速到达稳定值，抖动更小。

3.2 与其它改进滑模观测器算法对比分析

为了突出改进后的滑模观测器算法的优势，将其它文献上已经提出的改进方法在MATLAB中进行仿真。设置相同的仿真时间，将得到的结果与改进后的算法进行对比。基于连续切换的sat(x)函数滑模观测器算法结果如图8、图9所示。基于指数趋近律的滑模观测器算法结果如图10、图11所示。

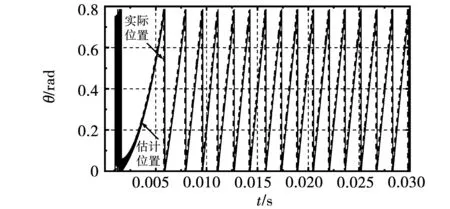
图8 基于sat函数的滑模观测器转子位置跟踪图Fig.8 Rotor position tracking diagram of sliding mode observer based on sat function

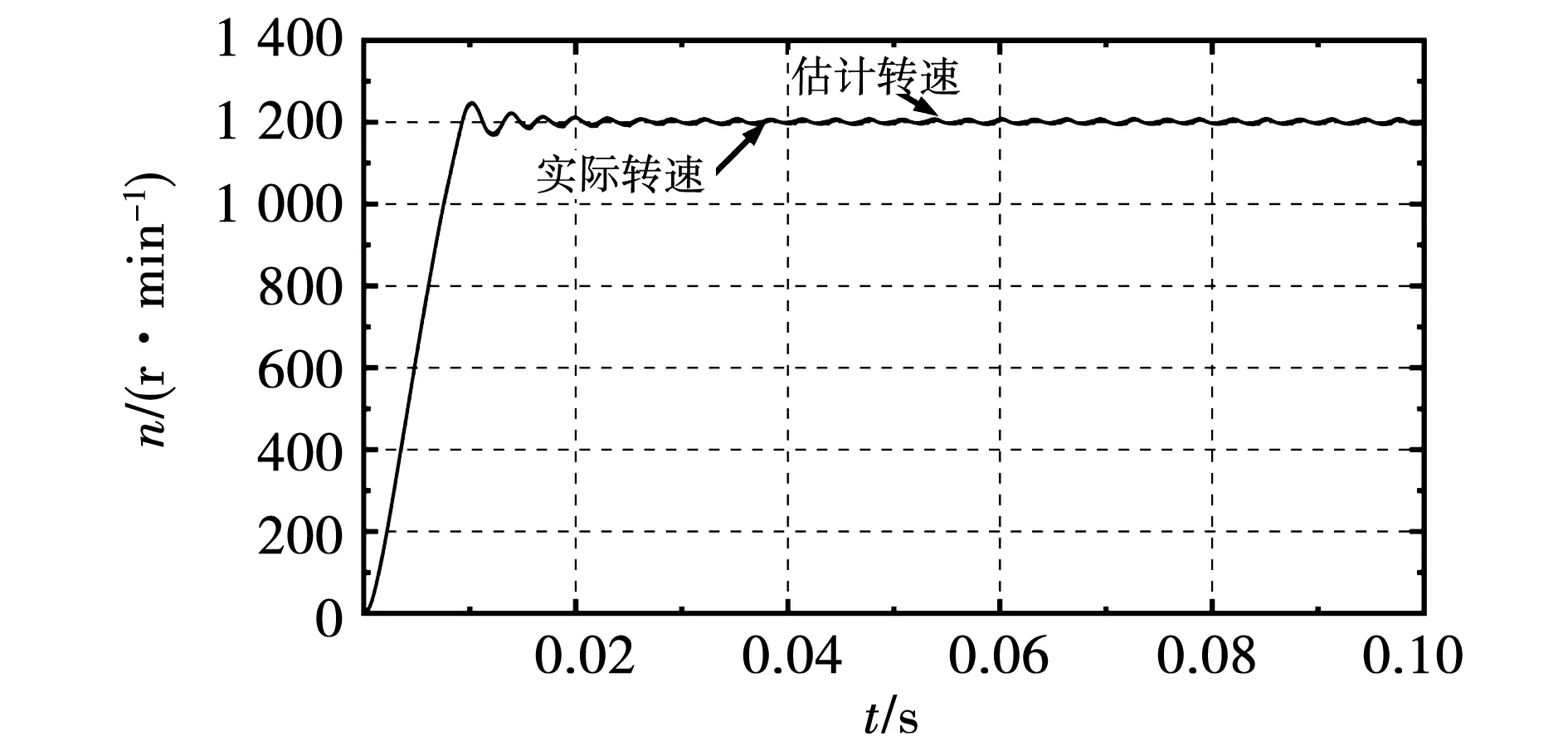
图9 基于sat函数的滑模观测器转速跟踪图Fig.9 Speed tracking diagram of sliding mode observer based on sat function

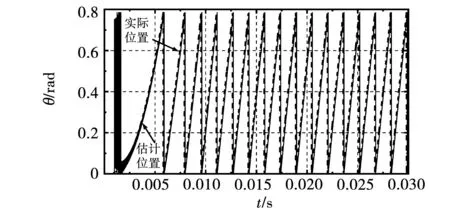
图10 基于指数趋近律的滑模观测器转子位置跟踪图Fig.10 Rotor position tracking diagram of sliding mode observer based on exponential reaching law

由图8和图10可知，转子估计的位置与实际位置较接近，相比于图4传统滑模观测器算法出现的抖振更小。由图9和图11可知，估计的转速在达到给定转速1 200 r/min后，上下波动出现抖振。与图5传统滑模观测器估计出的转速相比，其波动较小，在一定程度上抑制了抖振。但与图7改进后的滑模观测器算法相比，其转速波动较大，抑制抖振效果不明显。

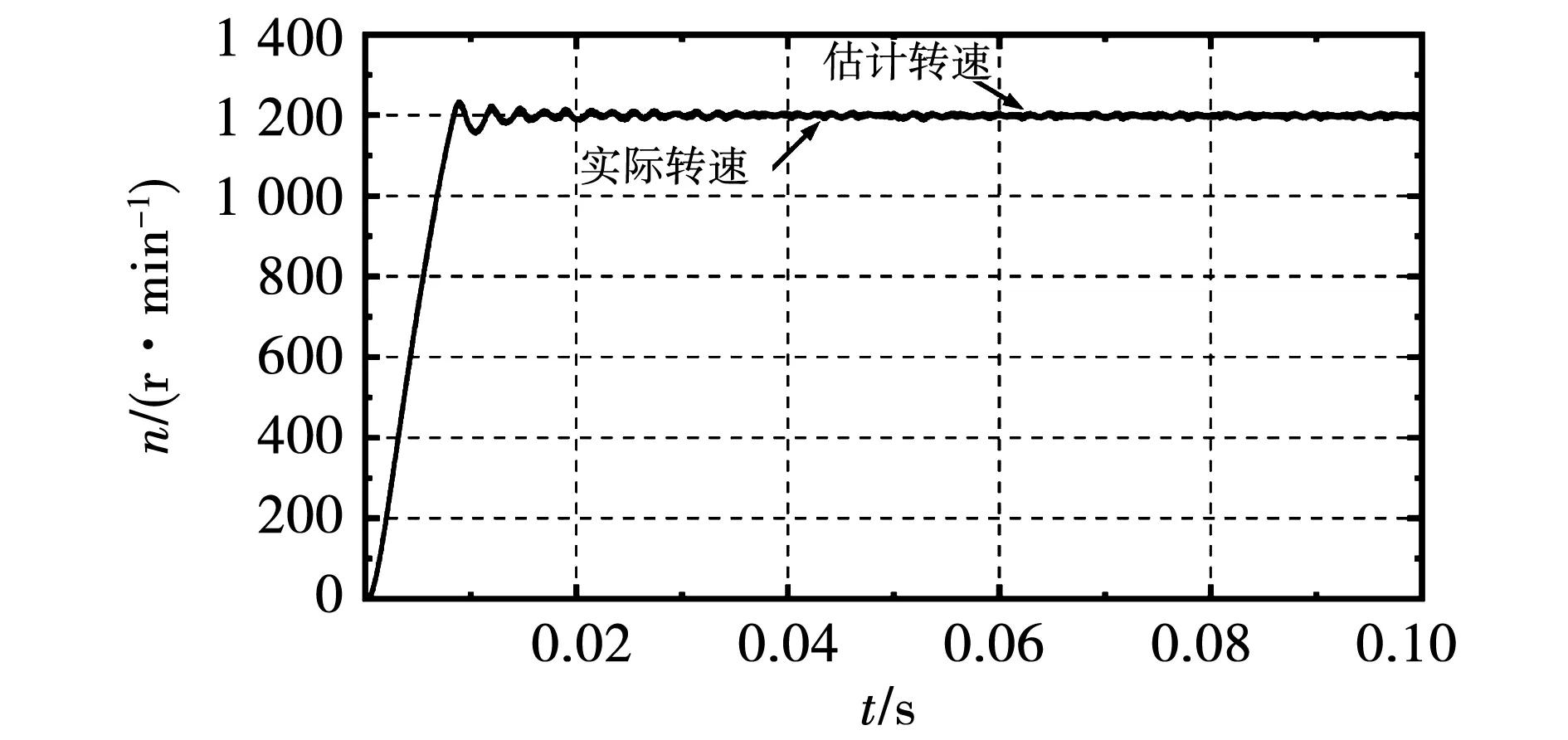
图11 基于指数趋近律的滑模观测器转速跟踪图Fig.11 Speed tracking diagram of sliding mode observer based on exponential reaching law

为了更直观的比较上述几种滑模观测器算法的效果，截取同样时间下的仿真结果，并将其绘制到一张图上进行比较。不同算法下的转子位置跟踪图如图12所示，不同算法下的转速抖动图如图13所示。图中所示内容由上到下依次为：传统滑模观测器算法结果、基于连续切换的sat(x)函数滑模观测器算法结果、基于指数趋近律的滑模观测器算法结果和改进后的滑模观测器算法结果。

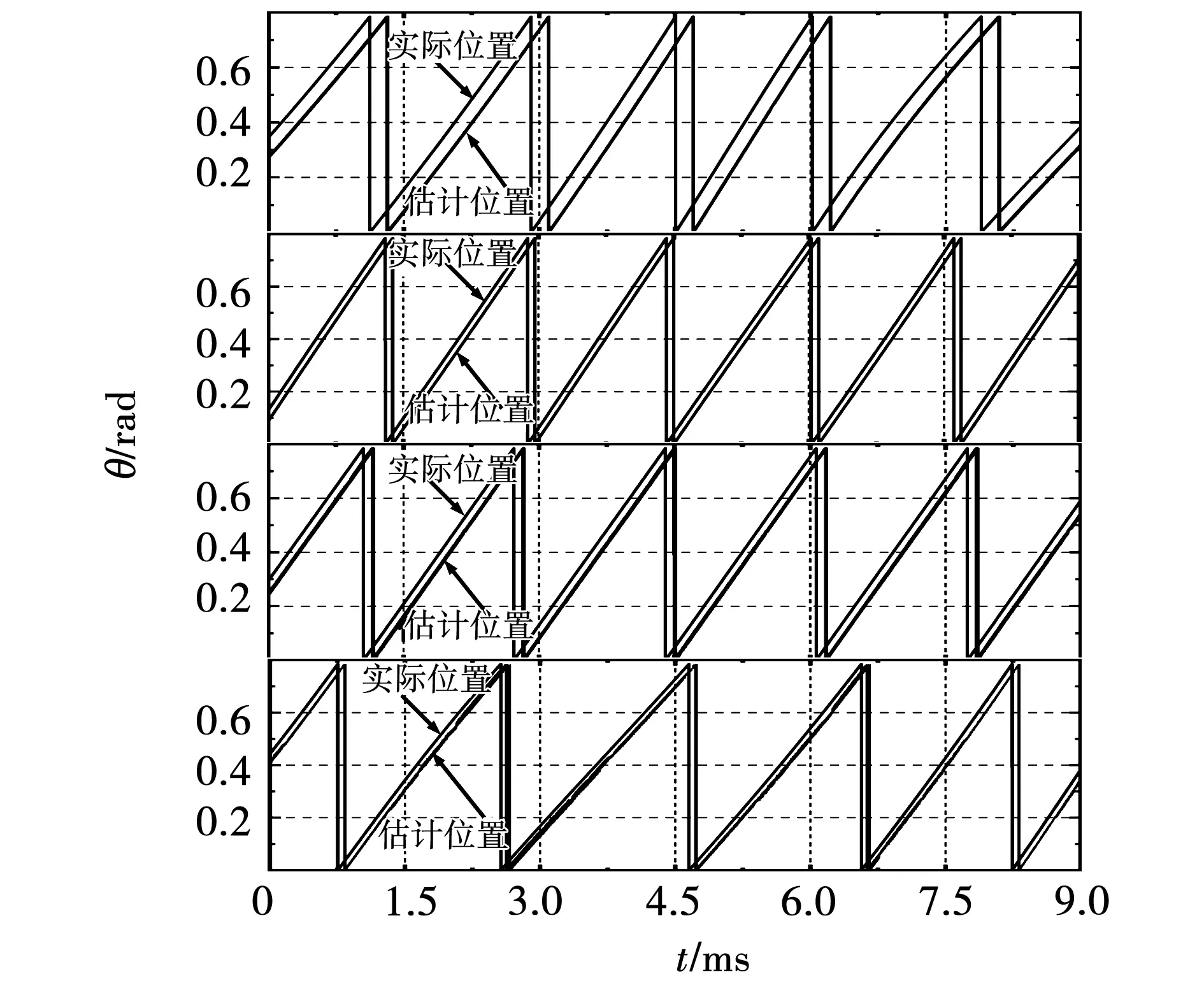
图12 不同算法下的滑模观测器转子位置比较图Fig.12 Rotor position comparison chart of sliding mode observer based on different algorithms

由图12可知，采用传统滑模观测器算法的估计位置与实际位置存在较大偏差，抖动明显。采用sat(x)函数或采用指数趋近律的改进滑模观测器算法的估计位置与实际位置较一致，出现的抖振较小。而改进后的滑模观测器算法的估计位置与实际位置更加贴近，误差更小，抑制抖振效果更明显。由图13可知，采用传统滑模观测器算法估计出的转速，抖动最大值约为20转，误差约为1.7%。采用sat(x)函数的改进滑模观测器算法估计出的转速，抖动最大值约为14转，误差约为1.2%。采用指数趋近律的滑模观测器算法估计出的转速，抖动最大值约为16转，误差约为1.3%。而改进后的滑模观测器算法估计出的转速，抖动最大值约为10转，误差约为0.8%。综上对比可知，改进后的滑模观测器算法能更好的抑制抖振，使估计值误差更小，更切合实际值。

图13 不同算法下的滑模观测器转速抖动比较图Fig.13 Comparison of the speed jitter of sliding mode observer under different algorithms

4 实验结果与分析

为了验证上述理论和仿真的正确性，搭建了永磁同步电机改进滑模观测器无传感器控制系统实验平台。实验平台如图14所示。

图14 永磁同步电机无感控制实验平台Fig.14 Experimental platform for sensorless control of permanent magnet synchronous motor

选取了TI公司生产的TMS320F28335芯片为电机控制板处理器，选用48 V永磁同步电动机以及功率驱动板、上位机、示波器。上位机端设定电机转速基准值为1 200 r/min，采用SVPWM调制方法，进行电机空载实验。为了验证无传感器控制的可行性，安装位置传感器，检测实时位置信号。实验结果如图15、图16所示。

图15 永磁同步电机空载转子位置角度跟踪图Fig.15 No load rotor position angle tracking diagram of permanent magnet synchronous motor

图16 永磁同步电机空载转速跟踪图Fig.16 No load speed tracking diagram of permanent magnet synchronous motor

由实验波形图可以得出，改进滑模观测器无传感器控制系统中转子估计位置角度与转子实际位置角度误差较小，抖振也较小。电机估计转速值与实际转速值也十分接近，误差在1%左右，略有抖振。

为了验证所提算法在不同工况下的可行性，将电机转速基准值同样设置为1 200 r/min，选取0.5 N·m的负载，采用SVPWM调制方法，进行电机负载实验。实验结果如图17、图18所示。

由图17、图18可知，改进滑模观测器无传感器控制系统在负载工况下，转子估计位置角度与转子实际位置角度差别很小接近一致，略有抖振。估计转速值十分贴近给定转速值，误差在0.9%左右。

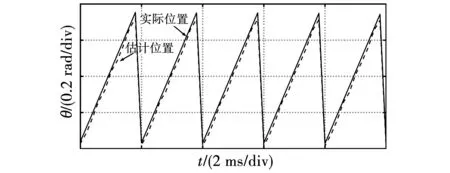
图17 永磁同步电机负载转子位置角度跟踪图Fig.17 Load rotor position angle tracking diagram of permanent magnet synchronous motor

图18 永磁同步电机负载转速跟踪图Fig.18 Load speed tracking diagram of permanent magnet synchronous motor

5 结 论

本文以表贴式永磁同步电机作为研究对象，通过对改进前后的滑模观测器无传感器控制系统进行仿真和不同工况下的实验，对结果进行对比。得出结论：采用在实数域上连续切换函数的改进滑模观测器能够减小系统抖振；结合指数趋近律控制能使系统更早地达到稳定值、更快地趋于稳定。通过对现有文献提出的改进滑模观测器算法和本文所提改进滑模观测器算法进行仿真对比。得出结论：将连续切换函数和指数趋近律控制结合的算法，可以在只采用连续切换控制函数算法或只采用指数趋近律控制算法的基础上，更进一步的抑制抖动，减小观测误差，使估计值更切合实际值。实验和仿真结合表明，本文提出的改进滑模观测器无传感器控制系统方案可行，稳定性更高。