考虑实际分布形式的水平受荷桩桩周土抗力分析方法
江 杰,付臣志,王顺苇,欧孝夺
(1. 广西大学土木建筑工程学院,广西,南宁 530004;2. 工程防灾与结构安全教育部重点实验室,广西,南宁 530004;3. 广西防灾减灾与工程安全重点实验室,广西,南宁 530004)
桩基础作为一种重要的基础形式,广泛应用于港口码头、海洋平台、风电铁塔、铁路桥梁等工程项目中,会承受由上部结构传递的水平力、竖向力、扭矩等复杂荷载作用[1-3]。对于水平受荷桩的分析,目前常用的方法有p-y曲线法、弹性地基反力法等[4-8]。然而,这些方法只能近似考虑水平向桩-土相互作用,无法考虑桩周土抗力的实际分布形式。对于只承受水平力的单桩,采用上述方法都能取得较好的计算精度,但对于水平力与其他荷载耦合作用的单桩,上述方法未能准确反映其他荷载对桩周土抗力的影响,使得桩基水平响应偏离实际。如:水平力与竖向力耦合作用时,不能考虑竖向摩阻力对环向摩阻力的影响[6-8];水平力与扭矩耦合作用时,不能考虑桩-土间的反向剪切作用[9]。因此,一种考虑实际分布形式的桩周土抗力理论分析方法亟待提出。
国内外学者对水平受荷桩桩周土抗力进行了大量研究,李洪江等[10]基于Vesic 圆孔扩张理论以均布荷载作用于被动侧桩周,近似认为土抗力沿桩径均匀分布。宋林辉等[11]基于考虑位移的朗肯土压力理论,根据桩周土的径向位移求解了径向土压力,以其水平分量作为桩周土抗力,一定程度上考虑了桩周土抗力的分布形式。值得指出的是,上述土抗力分析方法均未考虑环向摩阻力对土抗力的贡献,Smith[12]和Briaud 等[13]分析表明水平受荷桩桩周土抗力由径向土压力和环向摩阻力组成,并给出了两者沿桩周的分布模式,如图1所示。Prasad 等[14]和Lin 等[15]通过模型试验得到了桩周径向土压力,其沿桩周的分布形式与Smith[12]和Briaud 等[13]的结论一致。在此基础上,Zhang等[16]考虑径向土压力和环向摩阻力对土抗力的贡献,提出了极限土抗力计算公式,但无法给出不同桩身水平位移下土抗力沿桩周分布的具体值。此外,大多数土抗力分析方法是基于小直径柔性桩建立的,众多学者研究表明该法用于大直径桩的分析是不合理的[17-19]。因此,张小玲等[20]基于圆孔扩张理论并考虑环向摩阻力的影响,推导了适用于大直径桩的土抗力分析方法,但该法忽略了主动侧土体的抗力作用。此外,Zhu 等[21]基于桩土相互作用推导了适用于砂土地基刚性桩的土抗力分析方法,但该法考虑的环向摩阻力均为极限摩阻力,实际上环向摩阻力的大小与桩-土环向剪切位移有关。

图1 桩周土抗力分布Fig. 1 Distribution of soil resistance around the pile
综上所述,当前水平受荷桩桩周土抗力分析方法无法考虑其实际分布形式,不能用于分析水平力与其他荷载耦合作用下桩基水平响应的分析。因此本文对桩的主动侧和被动侧径向土压力的分布模式进行合理的假定,并考虑桩周环向摩阻力的影响,提出了桩周土抗力的计算方法,并通过算例验证了该方法的正确性。最后,对径向土压力水平分量和环向摩阻力水平分量随水平位移的变化规律进行探讨,通过拟合得到了近似表达式,为后续水平力与其他荷载耦合作用下桩基承载特性的研究奠定基础。
1 桩周径向土压力
1.1 桩周某点处径向土压力与径向位移关系的建立
水平受荷桩桩-土相互作用可分为2 个区域:桩移动方向前方,土压力增大,称为被动侧;桩移动方向后方,土压力减小,称为主动侧。当桩身水平位移为0 时,桩周土压力均为静止土压力。当桩顶受到水平荷载,桩身发生水平位移时,被动侧桩对土体的挤压作用使得桩周径向土压力由静止土压力逐渐增大到被动极限土压力,该过程可视为土体的加载过程。如图2 所示,Lin 等[15]给出了地面下352 mm、被动侧 α0=0°处的径向土压力与径向位移的关系。邓肯-张模型认为土体加载时的应力应变满足双曲线关系,因此本文假定被动侧桩周径向土压力随径向位移增大呈双曲线增大,对试验结果进行拟合,表达式为:
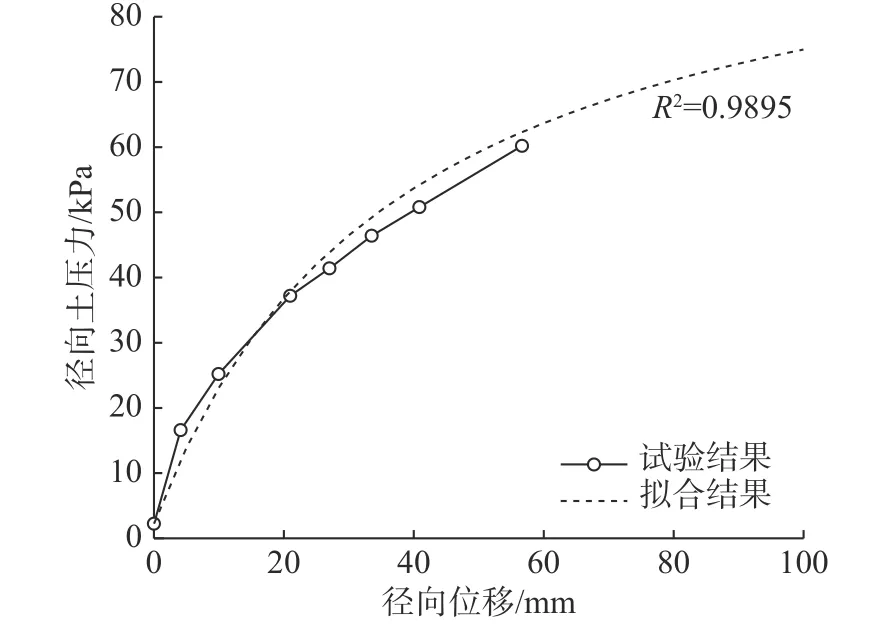
图2 径向土压力与径向位移关系Fig. 2 Relationship between radial soil pressure and radial displacement

式中:k为桩周某点的初始反力模量; σpu为被动侧径向土压力极限值;σ0为静止土压力,σ0=K0γz,K0为静止土压力系数,K0=1-sinφ′, γ为土的重度,φ′为土体的有效内摩擦角,z为深度;srp为被动侧桩周土的径向位移。
当桩身发生水平位移时,主动侧桩对土体的约束作用减弱,使得桩周径向土压力由静止土压力逐渐减小到主动极限土压力,水平位移继续增大时,主动侧土体与桩分离,桩受到的土压力变为0,该过程可视为土体的卸载过程。张磊[22]认为桩对土体的约束作用较弱,当桩身水平位移很小时主动侧土体就与桩脱离,因此主动侧土体对桩周土抗力的影响非常小。此外,Zhu 等[21]砂土地基中的模型试验结果显示,卸载时径向土压力随桩顶荷载减小呈线性减小。因此本文假定主动侧桩周径向土压力随径向位移增大呈线性减小,以此来近似考虑主动侧土压力,其表达式如下:
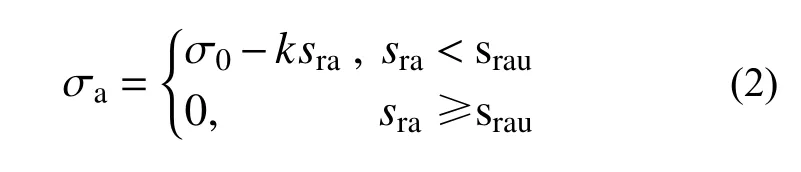
式中:sra为主动侧桩周土的径向位移;srau为主动侧桩周土的径向位移极限值,srau=(σ0-σau)/k,σau为主动土压力极限值, σau=Kaγz,Ka为主动土压力系数,Ka=tan2(45°-φ/2)。
综上所述,被动侧与主动侧的径向土压力模型可用图3 所示曲线表示。

图3 径向土压力模型Fig. 3 Radial soil pressure model
1)初始反力模量k的确定
水平荷载作用初始阶段,被动侧总土抗力增加,主动侧总土抗力减小,且两者具有相同的变化率,即被动侧总初始反力模量与主动侧总初始反力模量相等。取被动侧进行分析,如图4 所示,对被动侧每点的初始反力模量k积分可得总地基初始反力模量k′:


图4 被动侧初始反力模量分布Fig. 4 Distribution of the initial reaction modulus on the passive side
因此,桩周某点的初始反力模量为:

式中,d为桩径。
关于地基总初始反力模量k′的研究已经比较成熟,对于砂土地基,Carter[23]和Ling[24]假设地基总初始反力模量k′沿深度线性增加,并给出了考虑桩径影响的地基总初始反力模量表达式:

式中:nh为地基总初始反力模量的比例常数;dref为参考桩径,dref=1 m。
将式(5)代入式(4)可得到砂土地基中桩周某点的初始反力模量:

2)被动侧径向土压力极限值 σpu的确定
被动侧桩周某点的径向土压力极限值可按Zhang 等[16]推荐方法计算:

式中,Pu为极限土抗力。
对于砂土地基,朱斌等[25]对已有文献进行总结,建议极限土抗力按下式计算:

式中:Kp为被动土压力系数,Kp=tan2(45°+φ/2),φ为土体的内摩擦角; ξ为比例系数,取值范围为3~9。
将式(8)代入式(7)可得砂土地基中被动侧桩周某点的径向土压力极限值:

1.2 土的径向位移求解
桩身发生水平位移时会带动桩周土体一起变形,袁炳祥等[26]通过模型试验得到水平受荷桩桩周土体的位移场,其结果表明桩周土体沿着桩初始位置的径向移动;宋林辉等[11]得到的结论与袁炳祥等[26]的一致,并给出了桩周土径向位移的求解方法。
1)被动侧
根据对称性原理,取1/4 部分进行分析,如图5 所示。假设桩身任意深度z处桩截面水平位移为y,由图5 可知,A处土体移动到B处,径向位移量Srp为AB。

图5 被动侧桩周土体位移示意图Fig. 5 Soil displacement diagram of passive side of the pile
根据几何关系可得:


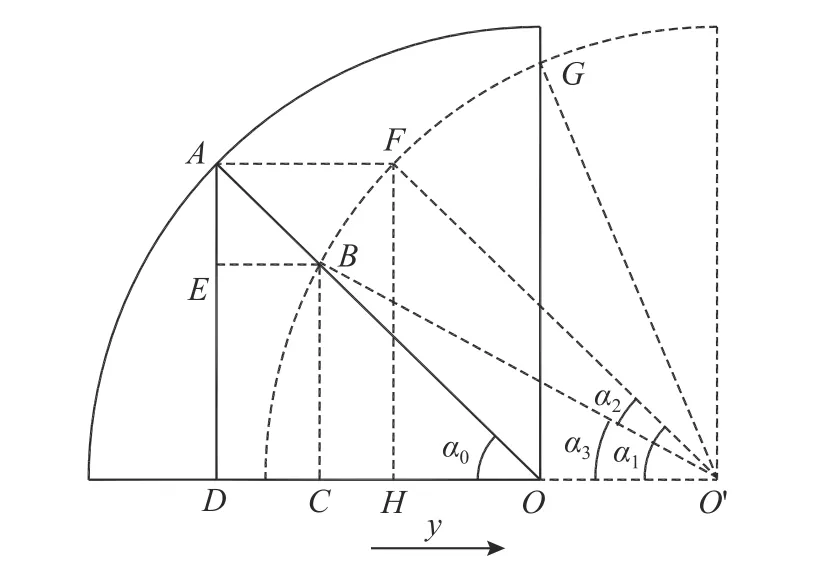
图6 主动侧桩周土体位移示意图Fig. 6 Soil displacement diagram of active side of the pile


1.3 桩周径向土压力求解
水平受荷桩桩周径向土压力分布如图7 所示,将桩周各点处的径向土压力投影到桩移动方向,即可得到水平受荷桩桩周径向土压力水平分量合力:

图7 桩周径向土压力分布Fig. 7 Distribution of radial soil pressure around pile

1)被动侧
将式(18)代入式(1)即可求得被动侧桩周某点的径向土压力,根据力学关系,将径向土压力水平分量沿桩周积分即可求得被动侧径向土压力水平分量合力:

2)主动侧
将式(25)代入式(2)即可求得主动侧桩周某点的径向土压力,根据力学关系,将径向土压力水平分量沿桩周积分即可求得主动侧径向土压力水平分量合力:

2 桩周环向摩阻力
2.1 双曲线荷载传递模型
Seed 等[27]在1955 年首次提出桩身荷载传递双曲线模型,国内外大量实验资料表明桩侧摩阻力与桩-土剪切位移之间的近似双曲线关系是存在的,这种双曲线模型也符合一般地基土的实际情况[28-29]。因此,本文采用双曲线模型模拟桩-土间的非线性剪切变形特性,如图8 所示。

图8 荷载传递模型Fig. 8 Load transfer model
桩周某点处的环向摩阻力与桩-土环向剪切位移的关系可表示为:


2.2 桩-土环向剪切位移求解
1)被动侧
根据图5,假设桩身任意深度z处桩截面水平位移为y,A处土体移动到B处,桩-土环向剪切位移量Sθp为BF。


2.3 桩周环向摩阻力求解
水平受荷桩桩周环向摩阻力分布如图9 所示,将桩周各点的环向摩阻力投影到桩移动方向即可得到水平受荷桩桩周环向摩阻力水平分量合力:

图9 桩周环向摩阻力分布Fig. 9 Distribution of friction resistance around pile
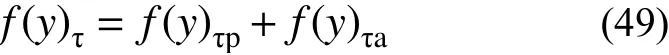
式中,f(y)τp、f(y)τa分别为被动侧、主动侧桩周环向摩阻力水平分量合力。
1)被动侧
将式(41)代入式(29)即可求得被动侧桩周某点的环向摩阻力,根据力学关系,将环向摩阻力水平分量沿桩周积分即可求得被动侧环向摩阻力水平分量合力:

3 桩周土抗力求解
桩周土抗力由径向土压力水平分量合力和环向摩阻力水平分量合力组成,两者相加可得本文考虑实际分布形式的水平受荷桩桩周土抗力计算公式:

4 方法验证
4.1 算例1
Lin 等[15]通过模型试验对水平受荷桩被动侧桩周土抗力(由径向土压力提供的土抗力)进行了研究。试验地基土采用砂土,不均匀系数Cu=6.5,曲率系数Cc=1.4,平均相对密度为32%,平均重度为16.5 kN/m3,含水率为2%,弹性模量为10 MPa,泊松比为0.2,内摩擦角为38°。空心钢管桩的弹性模量为210 GPa,桩外径为102 mm,厚度为6.4 mm,长度为1524 mm,入土深度为1394 mm。初始地基反力系数nh=9785 kN/m3,比例系数ξ=4.2。图10 给出了地面下352 mm 处桩周径向土压力沿桩周的分布规律,可以看出在不同桩顶荷载作用下,本文计算结果与试验结果均吻合较好,验证了本文方法的正确性。图11 还给出了地面下525 mm 处桩周土抗力随水平位移的变化规律,可以看出本文计算结果与试验结果总体上呈现良好的一致性,再次证明了本文方法的正确性。

图10 地面下352 mm 处桩周径向土压力沿桩周分布Fig. 10 Distribution of radial soil pressure around pile at depth of 352 mm under the ground

图11 地面下525 mm 处桩周土抗力随水平位移变化Fig. 11 Variation of soil resistance around pile with horizontal displacement at depth of 525 mm under the ground
4.2 算例2
朱斌等[25]开展了大位移条件下水平受荷单桩大比例模型试验。模型钢管桩长为7 m,直径为114 mm,壁厚为2.5 mm。试验地基土采用钱塘江粉砂土,土粒比重为2.69,塑限为22.6,液限为31.7,含水率为32.5%,饱和重度为17.5 kN/m3,相对密实度为0.23,有效内摩擦角为28.5°。初始地基反力系数nh=1850 kN/m3,比例系数 ξ =6.2。图12 给出了地面下3 倍桩径处桩周土抗力随水平位移的变化规律,可以看出本文计算结果与试验结果吻合较好,这表明用本文方法计算水平受荷桩桩周土抗力是合理的。

图12 地面下3 倍桩径处桩周土抗力随水平位移变化Fig. 12 Variation of soil resistance around pile with horizontal displacement at depth of three times pile diameter under the ground
5 参数分析
由前述分析可知,水平受荷桩桩周土抗力由径向土压力和环向摩阻力组成,为了探究径向土压力和环向摩阻力对土抗力的贡献程度随水平位移的变化规律,图13 分别给出了算例1 中泥面下3 倍桩径处和算例2 中地面下不同深度处,径向土压力水平分量合力Pσ、环向摩阻力水平分量合力Pτ与土抗力P之比的计算结果。由图可以看出,存在一个临界位移,当水平位移小于临界位移时,土抗力主要由环向摩阻力提供;当水平位移大于临界位移时,土抗力主要由径向土压力提供,这种变化趋势与Janoyan 等[37]的试验结果基本一致。此外,当水平位移达到5 mm 时,径向土压力和环向摩阻力对土抗力的贡献程度不再变化。算例1 中径向土压力、环向摩阻力分别贡献了75%、25%的土抗力,算例2 中径向土压力、环向摩阻力分别贡献了80%、20%的土抗力,这表明不同土层参数和桩基参数会影响径向土压力和环向摩阻力对土抗力的贡献程度,本文对此不做深入探讨。

图13 Pσ/P、Pτ /P 随水平位移变化Fig. 13 Variation of Pσ /P、Pτ /P with horizontal displacement
Prasad 等[14]通过模型试验研究了径向土压力水平分量沿桩径的分布形式,得到了不同深度处径向土压力水平分量平均值 σph,mea与最大值σph,max之比为0.8。笔者对算例1 和算例2 中的结果进行处理,得到了 σph,mea/σph,max随水平位移的变化规律,结果见图14。可以看出,水平位移很小时,该比值接近1.0;随着水平位移增大,该比值快速减小到0.8 而趋于稳定。这是因为,当水平位移接近0 时,被动侧桩周各点处所受的土压力相等,随着水平位移的增大,被动侧桩周各点处径向土压力发挥快慢不同,并且被动侧桩周各点处的径向土压力水平分量比例也不同。此外,σph,mea/σph,max表示桩侧径向土压力水平分量不均匀分布的形状系数,可用 η表示[13],因此考虑水平位移影响的 η可按下式计算:

图14 σph,mea /σph,max 随水平位移变化Fig. 14 Variation of σph,mea /σph,max with horizontal displacement

式中: σph,mea为不同水平位移下径向土压力水平分量平均值; σph,max为不同水平位移下径向土压力水平分量最大值。上述分析表明,极限状态下可取 η =0.8。
为了进一步探究径向土压力水平分量沿桩径的分布规律,将算例1 和算例2 的结果进行归一化处理,结果见图15。由图可以看出,两个算例归一化处理后的结果基本重合,通过拟合得到被动侧桩周某点处径向土压力水平分量与径向土压力水平分量最大值的关系:

图15 σph,i /σph,max 随sin α0 的变化规律Fig. 15 Variation of σph,i /σph,max with sin α0

当桩身水平位移y已知时,通过式(55)可以很方便地求解被动侧桩周某点的径向土压力水平分量。
图16 给出了算例2 中不同深度处环向摩阻力水平分量平均值τph,mea与最大值τph,max之比随水平位移的变化规律,可以看出该比值随水平位移增大逐渐减小到0.9 而趋于稳定。此外,τph,mea/τph,max表示桩侧环向摩阻力水平分量不均匀分布的形状系数,可用 ξ表示[13],因此考虑水平位移影响的ξ的表达式为:
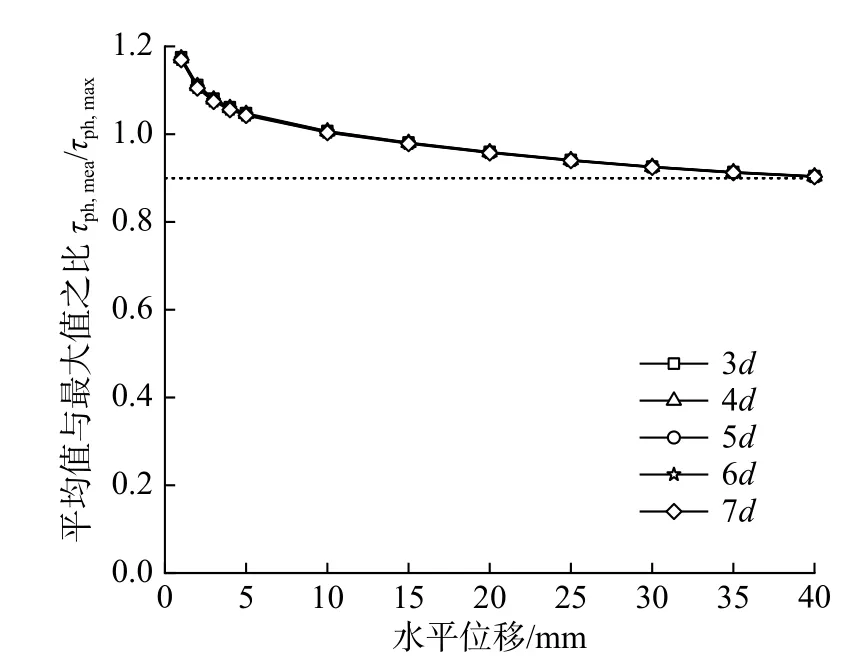
图16 τph,mea /τph,max 随水平位移变化Fig. 16 Variation of τph,mea /τph,max with horizontal displacement

式中:τph,mea为不同水平位移下环向摩阻力水平分量平均值;τph,max为不同水平位移下环向摩阻力水平分量最大值。上述分析表明,极限状态下,可取 ξ =0.9。
为了进一步分析环向摩阻力水平分量沿桩径的分布规律,图17 给出了算例2 中水平位移为40 mm 时泥面下不同深度处环向摩阻力水平分量的计算结果。可以看出不同深度处的环向摩阻力水平分量沿桩径的分布相同,最大值位于α0=±45°处。此外,不同水平位移下环向摩阻力水平分量最大值位置不同,但都介于-48°~-42°或42°~48°之间。取-48°~-42°范围内的环向摩阻力进行分析,图18 给出了泥面下3 倍桩径处不同水平位移下环向摩阻力水平分量的计算结果,可以看出该范围内环向摩阻力水平分量值几乎完全相等,因此不同水平位移下环向摩阻力水平分量最大值均取α0=±45°处的值。

图17 地面下不同深度处环向摩阻力水平分量计算结果Fig. 17 Calculation results of horizontal component of friction resistance at different depths under the ground

图18 不同水平位移下环向摩阻力水平分量计算结果Fig. 18 Calculation results of horizontal component of friction resistance at different displacements
在此基础上,对环向摩阻力水平分量进行归一化处理,结果见图19。可以看出归一化处理后的结果基本重合,通过拟合得到被动侧桩周某点的环向摩阻力水平分量与环向摩阻力水平分量最大值的关系:

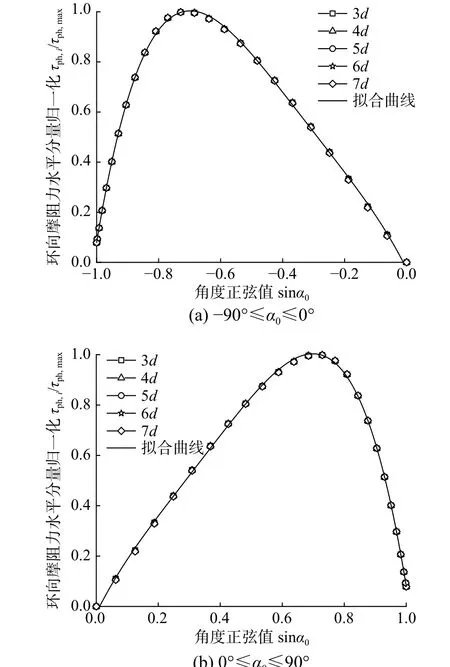
图19 τph,i /τph,max 随sin α0 的变化规律Fig. 19 Variation of τph,i /τph,max with sin α0

6 结论
鉴于当前水平受荷桩桩周土抗力分析方法无法考虑其实际分布形式,本文分别建立了桩周被动侧、主动侧的径向土压力与径向位移的关系,并对环向摩阻力的初始刚度进行修正,推导了考虑实际分布形式的桩周土抗力计算方法。通过算例验证了本文方法的正确性,揭示了径向土压力水平分量和环向摩阻力水平分量的变化规律。通过计算和分析得到的主要研究结论如下:
(1)本文假定桩周径向土压力随径向位移增加,在被动侧呈双曲线形式增大,在主动侧呈线性减小,通过算例分析表明该模型可以很好地预测桩周径向土压力。
(2)本文方法考虑了桩周土抗力实际分布形式,计算结果与试验结果吻合较好,可为水平力与其他荷载耦合作用下的桩基分析提供参考。
(3)径向土压力和环向摩阻力对土抗力的贡献程度与水平位移有关,存在一个临界位移,当水平位移小于临界位移时,土抗力主要由环向摩阻力提供;当水平位移大于临界位移时,土抗力主要由径向土压力提供。
(4)极限状态下,桩侧环向摩阻力水平分量最大值位于 α0=±45°处,通过拟合公式可以很方便地计算该最大值;桩侧径向土压力水平分量不均匀分布的形状系数 η=0.8;桩侧环向摩阻力水平分量不均匀分布的形状系数 ξ=0.9。

