一道椭圆试题的解法探究及推广

贵州省六盘水市第二中学 (553401) 张 东

一、试题呈现

(1)求椭圆E的标准方程；

(2)过F2作两条互相垂直的直线与E分别交于A，B和C，D,若M，N分别为AB和CD的中点.证明：直线MN恒过定点，并求出定点坐标.

试题评析：第(1)问以椭圆的基本概念入手，起点低，注重考查数学的基础知识、基本概念，第(2)问考查直线与椭圆的位置关系、中点弦、定点问题.试题立足通性通法，注重数学本质，试题设计多层次，入口宽，解法多样，考查学生数学运算，逻辑推理，直观想象的数学核心素养，试题有很好的教育引导价值.

二、解法探究

这里我们只探讨第(2)问,给出三种常见解法.

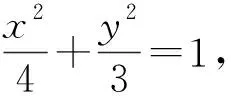
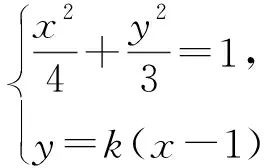
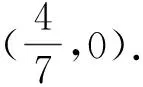
点评：联立直线与椭圆方程，由韦达定理即可求出点M，N坐标，解法立足通性通法，淡化技巧，思路清晰明了，循序渐进，思维量小，但计算量大，学生需具备扎实的数学运算，逻辑推理素养，才能完备性地求出定点.

点评：从圆锥曲线点差法的思想角度入手，探寻动点M，N满足的曲线方程(对称中心不在坐标原点的椭圆)，直线MN恒过的定点即可转化为学生熟悉的解析几何问题.

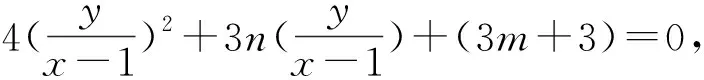
点评：在解法二的基础上，利用动点M，N满足的曲线方程，另辟蹊径，构造关于直线F2M，F2N的齐次化方程，引入韦达定理即可求出直线MN恒过的定点，该方法有一定的技巧性，可作为学生复习备考的选讲内容，拓宽学生的解题思路.

三、问题一般化

由于试题中直线AB和CD的任意性，我们可把定点F2拓展到椭圆内部任意一点，得到问题的一般性结论，为了简化证明，这里我们沿用解法三中齐次化[1]的方法给出证明过程.

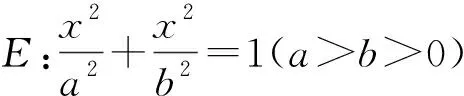
四、问题推广

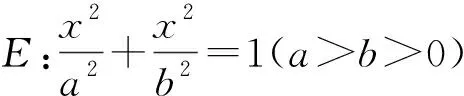
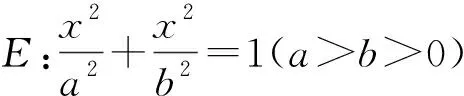
五、问题引申

性质5 已知点P(x0,y0)为抛物线E：y2=2px(p>0)内部任意一点，过P点作两条相交的直线与E分别交于A，B和C，D,且M，N分别为AB和CD的中点.若kAB·kCD=λ，则直线MN恒过定点

性质4、性质5证明过程可类比性质性质2、性质3完成，限于篇幅，这里不再一一赘述.