一道抛物线试题的探究与推广

广东省佛山市第一中学 (528000) 刘振兴

极点与极线是高等几何中的重要内容，虽然不是《高中数学课程标准》规定的学习内容，也不属于高考考查的范围，但由于极点与极线是圆锥曲线的基本特征，因此在高考试题和各地模拟题中必然会有所反映，自然也会成为高考试题中的命题背景.

在文[1]中作者给出如下定义1和定理1的证明.

定义1 已知圆锥曲线Γ:Ax2+Cy2+2Dx+2Ey+F=0，则称顶点P(x0,y0)和直线l:Ax0x+Cy0y+D(x+x0)+E(y+y0)+F=0圆锥曲线Γ的一对极点和极线.

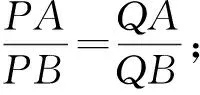
一、原题再现

题目(2021年佛山一模)已知抛物线C:y2=2px(p>0)的焦点为F，准线l交x轴于点K，过F作倾斜角为α的直线与C交于A,B两点，若∠AKB=60°，则sinα=.

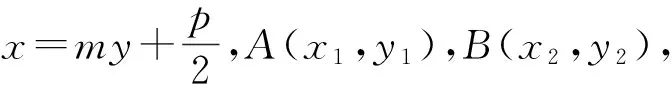
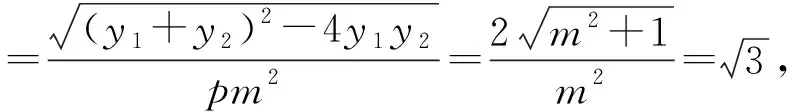
评析：解法一是常规解法，计算量偏大.解法二计算过程简洁，先证结论:∠AKF=∠BKF,再利用这个结论快速解答.

二、拓展推广

若把题目中过焦点F的直线推广到过一般点Q的直线，结论也成立.

推论1 已知抛物线Γ:y2=2px(p>0),点P(-m,0),Q(m,0)，过Q作直线交抛物线于A,B两点，则∠APQ=∠BPQ.

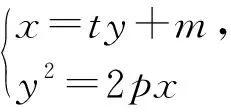
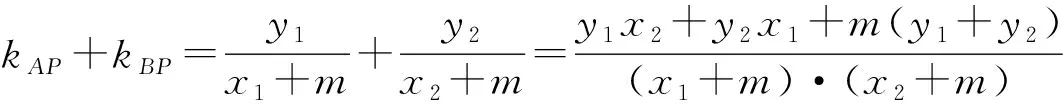
将推论1中抛物线的结论推广到椭圆和双曲线中，结论也成立.

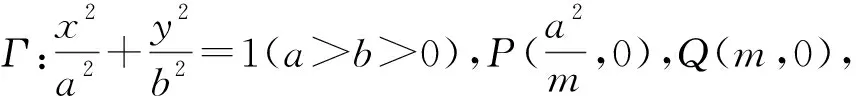
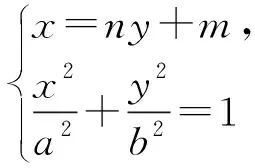
三、高考中的应用

推论1,2和3应用很广，以下两道高考题的命题背景就是推论2和推论1.

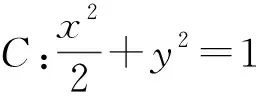
(1)当l与x轴垂直时，求直线AM的方程；

(2)设O为坐标原点，证明：∠OMA=∠OMB.

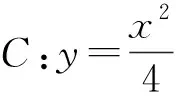
四、背景分析

上述推论1，2，3其实是圆锥曲线极点与极线的统一结论，见文献[2].

性质1 如图1、2，已知点P,Q是圆锥曲线Γ的对称轴l上两点(不在Γ上)，若P,Q关于圆锥曲线Γ调和共轭，过Q任作一条割线，交Γ于点A,B,则直线PA,PB与对称轴所成的角相等.

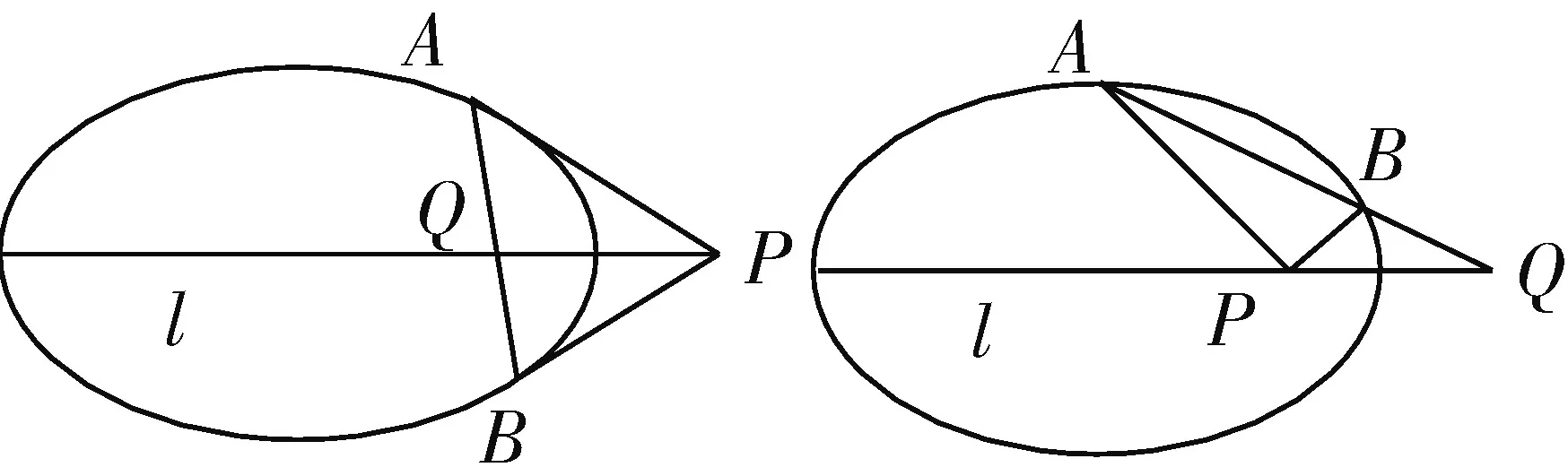
图1 图2

极点与极线的性质有很多，而且经常是圆锥曲线试题的命题背景，在复习备考中需重视.

性质2 如图3，设圆锥曲线Γ的一个焦点为Q，与Q相对应的准线为l.

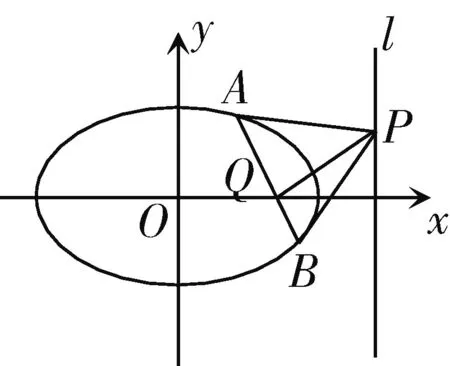
图3

(1)若过点Q的直线与圆锥曲线Γ相交于A,B两点，则Γ在A,B两点处的切线的交点P在准线l上，且PQ⊥AB;

(2)若过准线l上一点P作圆锥曲线Γ的两条切线，切点分别为A,B，则直线AB过焦点Q，且PQ⊥AB;

(3)若过焦点Q的直线与圆锥曲线Γ相交于A,B两点，过Q作PQ⊥AB交准线l与点P，则连线PA,PB是圆锥曲线Γ的两条切线.

性质3 如图4，已知点P,Q和有心圆锥曲线Γ，直线PQ经过Γ的中心O，与Γ交于点A,B(点A在P,Q之间).若P,Q关于Γ调和共轭，则OP·OQ=OA2；反之，若有OP·OQ=OA2，则点P,Q关于Γ调和共轭.

图4 图5

性质5 如图6、7，已知点Q在圆锥曲线Γ的对称轴上，直线l垂直于该对称轴，过Q作直线交Γ于点A,B，P为l上任意一点.若点Q与直线l是Γ的一对极点与极线:

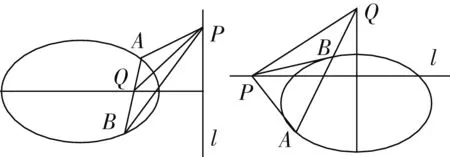
图6 图7

(1)如图6，当对称轴是x轴或平行于x轴时，kPA+kPB=2kPQ；

极点与极线在最近几年全国卷高考试题中陆续出现，例如2015全国1卷理科20题，2018全国1卷理科19题，2020高考全国1卷理科第20题.作为一名高中数学老师，应当了解极点与极线的概念，掌握有关极点与极线的基本性质，只有这样，才能“识破”试题中的蕴含的有关极点与极线的知识背景，进而把握命题规律.