两个猜想不等式的加权推广

山东省邹平双语学校 (256200) 姜坤崇

宋庆老师在文[1]中给出了如下两个猜想不等式(这里分别记为问题1、2)：

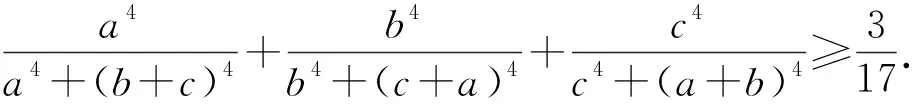
证明中用到了“以曲代曲”的新颖方法,体现了数学的美妙与神奇.笔者对此两个不等式也进行了研究，发现它们不但成立，而且还可以加权推广，得到以下两个命题.

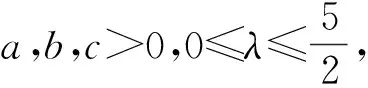
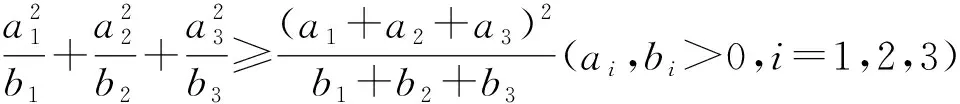
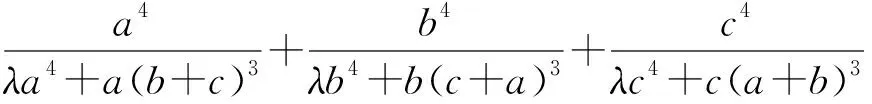
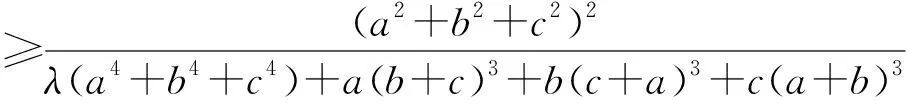
于是要证原不等式成立，只需证：

又由二元均值不等式得a2b2+c2a2≥2a2bc,b2c2+a2b2≥2b2ca,c2a2+b2c2≥2c2ab,以上三个不等式相加且两边同除以2得a2b2+b2c2+c2a2≥a2bc+b2ca+c2ab.而2λ+13>0,所以(2λ+13)(a2b2+b2c2+c2a2)≥(2λ+13)(a2bc+b2ca+c2ab)③.

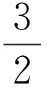
②+③+④即得①式，从而原不等式得证.

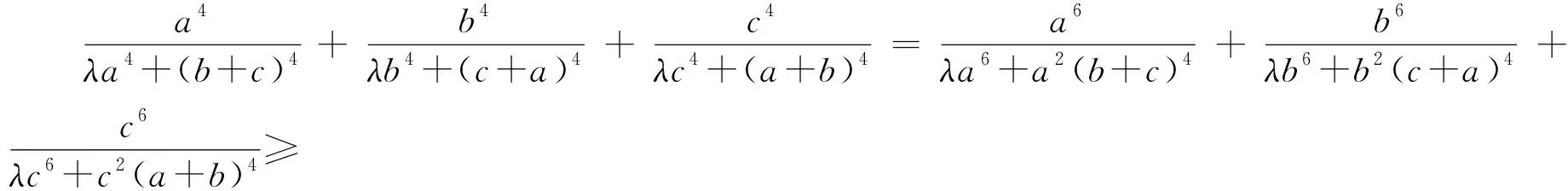
于是要证原不等式成立，只需证：

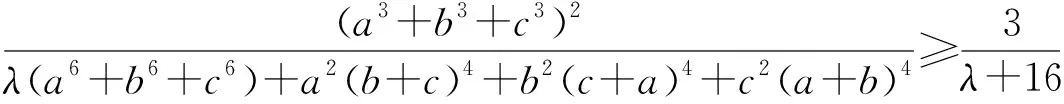
由3元均值不等式得2a6+b6≥3a4b2,a6+2b6≥3a2b4,2b6+c6≥3b4c2,b6+2c6≥3b2c4,2c6+a6≥3c4a2,c6+2a6≥3c2a4,以上6个不等式相加得6(a6+b6+c6)≥3(a4b2+a2b4+b4c2+b2c4+c4a2+c2a4)⑥.

又由3元均值不等式得a6+a3b3+b3c3≥3a3b2c,a6+b3c3+c3a3≥3a3bc2,b6+b3c3+c3a3≥3b3c2a,b6+c3a3+a3b3≥3b3ca2,c6+c3a3+a3b3≥3c3a2b,c6+a3b3+b3c3≥3c3ab2,以上6个不等式相加且两边同乘以4得8(a6+b6+c6)+16(a3b3+b3c3+c3a3)≥12(a3b2c+a3bc2+b3c2a+b3ca2+c3a2b+c3ab2)⑦.

最后再由3元均值不等式得a6+b6+c6≥3a2b2c2,a3b3+b3c3+c3a3≥3a2b2c2,而2(1-λ)≥0,2(λ+8)>0,所以2(1-λ)(a6+b6+c6)≥6(1-λ)a2b2c2⑧.

2(λ+8)(a3b3+b3c3+c3a3)≥6(λ+8)·a2b2c2⑨.

⑥+⑦+⑧+⑨即得⑤式，从而原不等式得证.

显然，在命题1、2的不等式中令λ=1可分别得问题1、2中的不等式，所以命题1、2中的不等式分别是问题1、2中不等式的推广.