从一道课本习题看向量的数量积

江西省莲花中学 (337100) 周秋良

向量的数量积是向量运算的一个重点内容，也是高考命题的热点问题.本文利用一道课本习题从多角度、分层次对问题的求解进行探索，对向量数量积的求解方法进行归纳总结，并对问题进行变式训练，同时对数学习题的设置作了一点思考.

1.习题再现

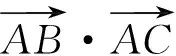
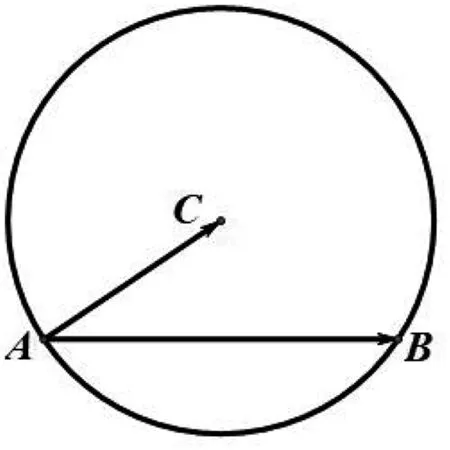
图1

2.试题分析

这是一道题干简洁、精炼，内涵丰富的应用性题目，考查了向量数量积的几何意义和向量数量积的坐标运算，这是学生必备的知识要求.本题考查学生的逻辑思维能力、运算求解能力、转化化归能力和数学建模能力.学生通过明晰运算对象，依据向量数量积的几何意义或通过建立适当的平面直角坐标系，将问题进行转化，从而解决问题.而解决这类问题的常见方法有：向量数量积定义法、坐标法、极化恒等式法、基底转化法、向量数量积余弦定理法、四边形对角线数量积法等.

3.解法探究

(1)利用向量数量积的几何意义求解.

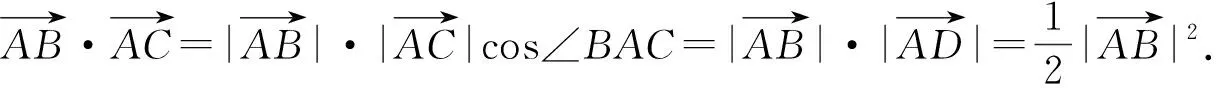
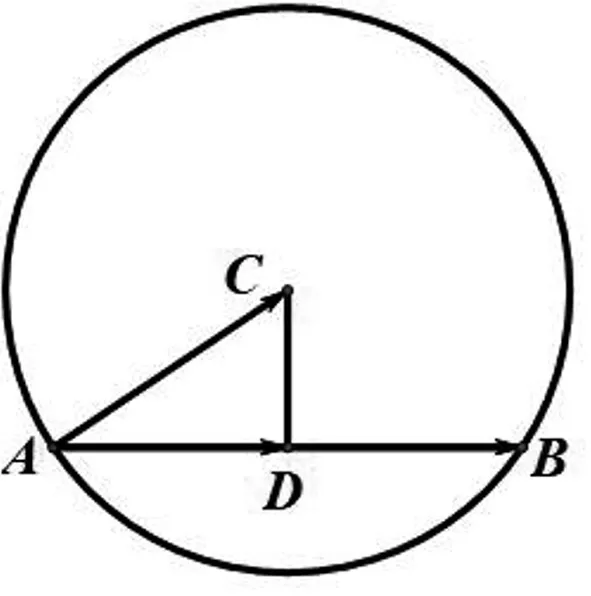
图2

(2)对向量进行转化，结合余弦定理进行求解.

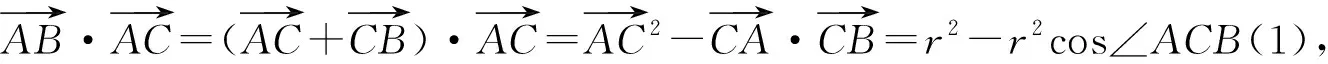
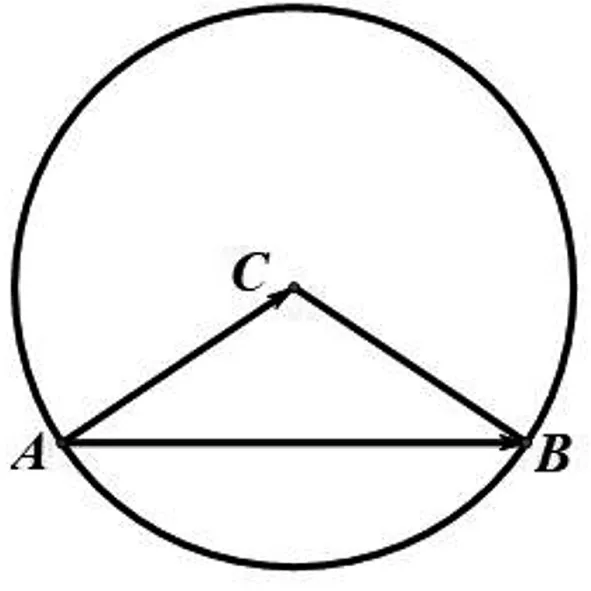
图3

(3)建立适当的直角坐标系进行求解.

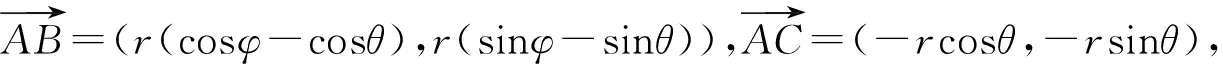
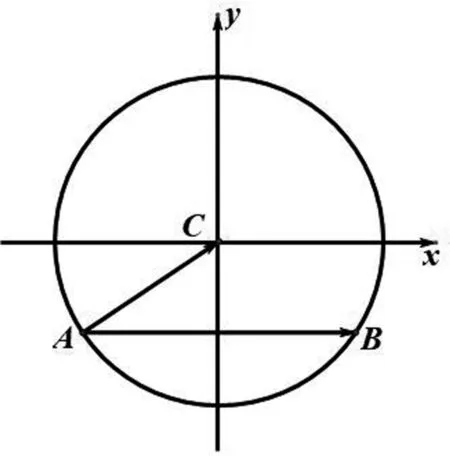
图4

(4)构造几何图形使问题得到求解.

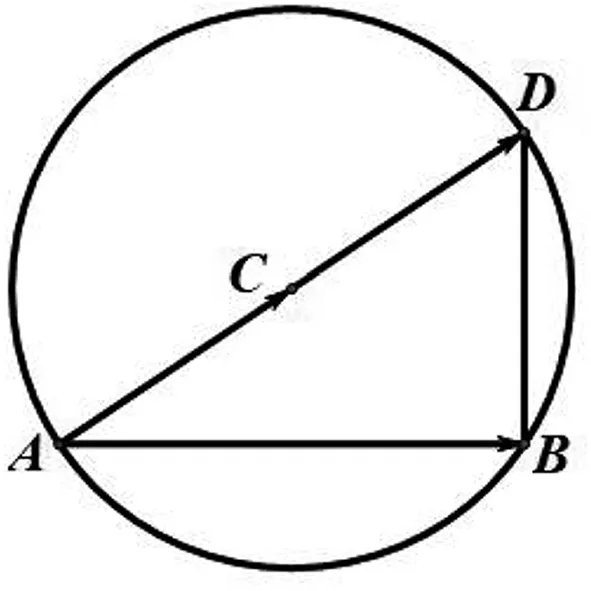
图5

(5)利用向量数量积余弦定理求解.

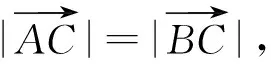
(6)利用极化恒等式求解.

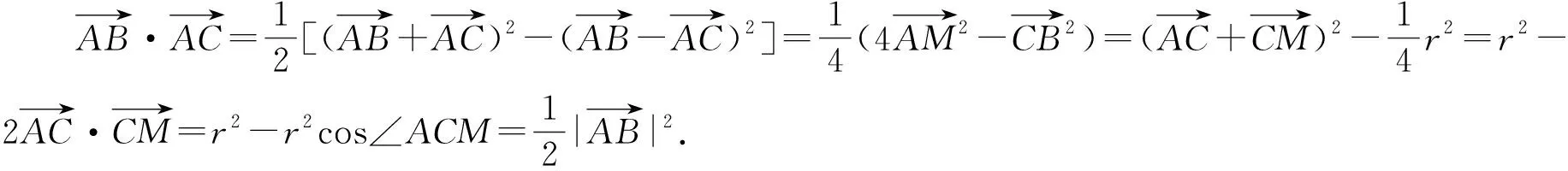
4.变式训练

A.(-2,6) B.(-6,2)

C.(-2,4) D.(-4,6)

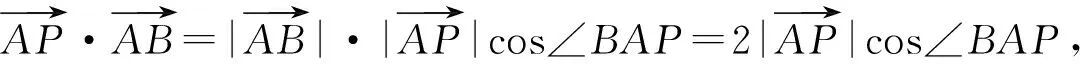
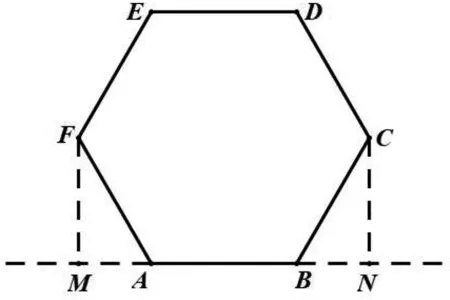
图6

评析：此解法利用数量积的几何意义，将数量积的取值范围转化为几何量的取值范围，具有直观性的特点.利用投影法求数量积时，要注意数量积的正负与向量夹角的关系.当然，也可以通过建立直角坐标系对问题进行求解.

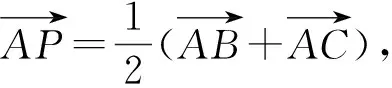
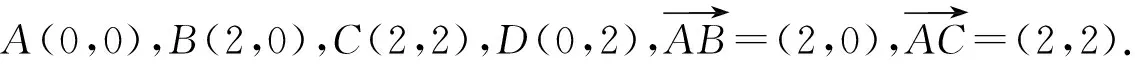
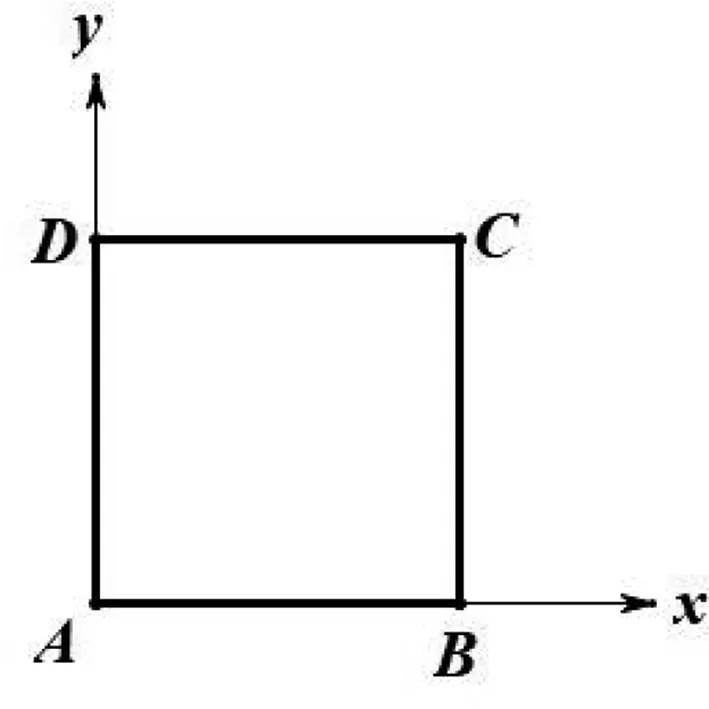
图7

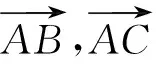
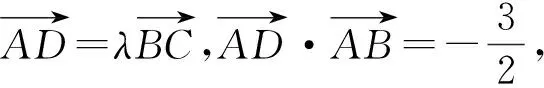
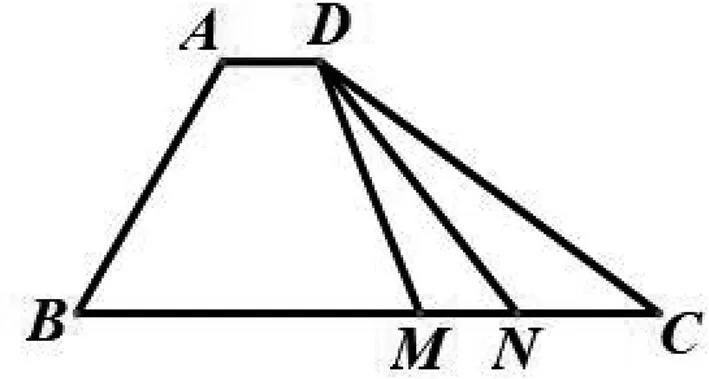
图8

评析：此处第一空直接利用已知条件求解，第二空利用极化恒等式对问题进行转化，大大减少了运算量，值得关注.

.

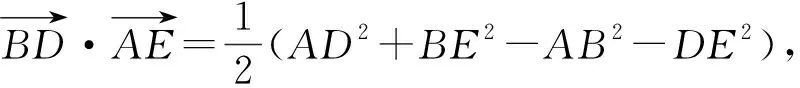
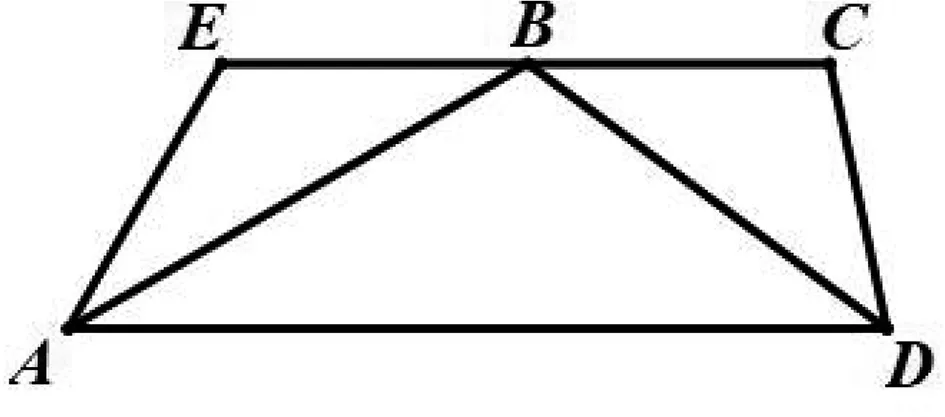
图9

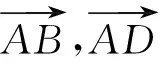
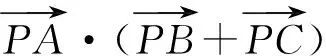
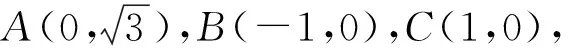
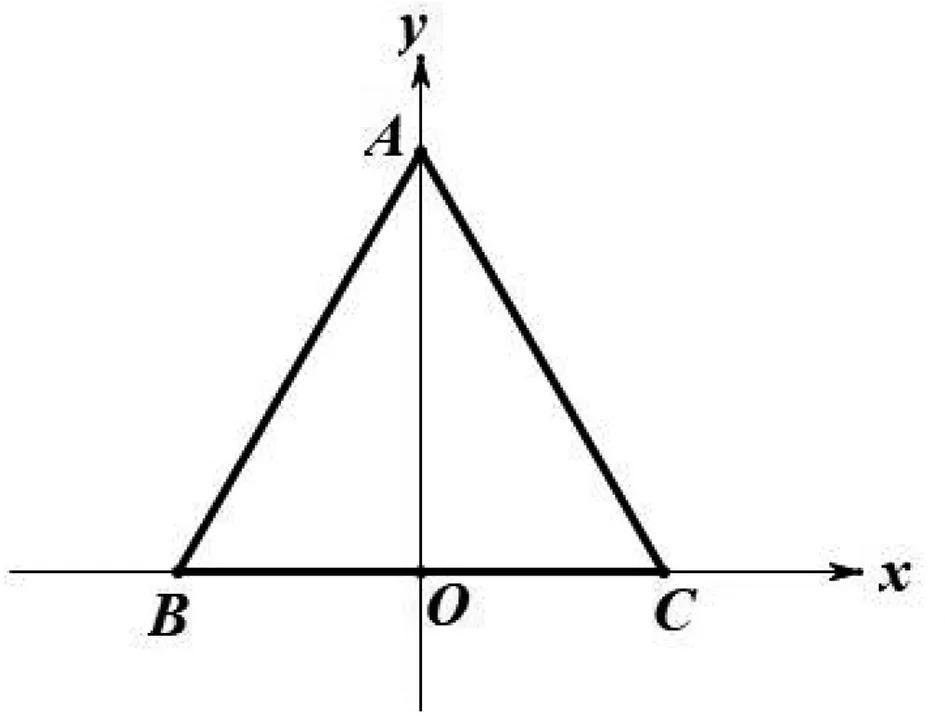
图10

评析：此处用建立直角坐标系，利用数形结合思想将问题进行转化.

5.反思总结

《普通高中数学课程标准(2017年版)》明确指出，高中数学课程以学生发展为本，要面向全体学生，实现人人都能获得良好的数学教育，不同的人在数学上得到不同的发展.基于这一课程理念，在日常的教学过程中，数学习题的设置是否合理就显得尤为重要，不仅要注重习题的有效性，还要科学、准确地把握习题的容量、难度，防止“题海战术”.

一方面，数学学科核心素养的形成，要求数学习题的设置应该具有层次性.数学的产生、发展、应用的过程是一个有序多级的系统，习题的设置应由浅入深，层层递进.教学中应给学生搭好学习数学、解决数学问题的脚手架，让学生在掌握基本知识、基本技能的同时，感悟数学的基本思想，累积数学思维的基本经验.

另一方面，“四基”、“四能”的课程目标的实现，要求数学习题的设置应该具有针对性.史宁中教授认为，数学教学目标就是培养学生学会用数学的眼光观察现实世界，会用数学的思维思考现实世界，会用数学的语言表达世界.在日常的数学学习过程中，用数学语言表达最多的就是在解决数学问题的时候，如果数学习题的设置没有针对性，那学生就很难真正学会数学语言，也不可能懂得怎样用数学思维思考现实世界，更不要说用数学语言表达世界了.

再之，由《中国高考评价体系》对高考命题的要求，强调数学命题的设置应该具有探究性.“一核”“四层”“四翼”的高考评价体系，让高考的命题有了明确的方向，对“创新性”的要求，对教育公平的助推，使得高考试题具有明显的探究性.为了更好地适应高考评价体系的要求，数学习题的设置就应该具有探究性.让学生的综合素质得到有效的培养，真正成为德智体美劳全面发展的人.

总之，合理地设置数学习题，学生通过有效地解决数学习题，能提高学习数学的兴趣，增强学好数学的自信心，养成良好的数学学习习惯，发展自主学习的能力.