基于低秩分解的异常步态活动图像序列识别

邱妍妍，高 增

(1. 兰州财经大学陇桥学院，甘肃 兰州 730000；2. 苏丹依德利斯师范大学，马来西亚 35900)

1 引言

步态主要是指人们行走时的姿态，是在远距离可监视的唯一行为特征[1]。异常步态活动图像序列识别技术的研究主要用于人体行为检测及预测，或记录行走路径，防止走丢等。通常步态行为特征具有明显的协同性，因此当步态处在一定的异常行为状态，如摔倒、疾病突发、走失等情况发生，常伴有明显的行为特征变化。

常规改变的主要有动作、位置、表情等生理参数，因此对异常步态活动图像进行收集和整理和分析，有利于正确判断异常行为状态，对人体起到保护作用[2]。目前具有代表性的识别方法主要有以下几种：张昊[3]提出基于动态二维图像序列的三维步态识别方法探究。利用动态二维图像序列指代当前三维步态的不同部分，完成异常步态识别。该方法步骤较为复杂；何正义[4]等专家提出一种集成卷积神经网络和深信网的步态识别与模拟方法。根据步态信号方向和角度变化处理图像序列，结合卷积神经网络识别图像序列，该方法识别精度相比前一种方法较好，但仍不理想。宋相法[5]等专家提出基于L(2，1)范数稀疏特征选择和超法向量的深度图像序列行为识别方法。将行为特征转化为L(2，1)范数稀疏特征，计算L(2，1)范数稀疏特征的超法向量，识别深度图像的序列。该方法在计算过程中，易出现误差，导致识别精度较低。

针对上述问题，提出一种基于低秩分解的异常步态活动图像序列识别方法。并进行仿真，验证了该方法的优越性。

2 异常步态活动图像序列的识别

2.1 基于Zermike矩的图像序列特征提取

为了描述步态运动过程，需要提前设定步态历史图像序列，作为标准运动序列。

设当前用B(x，y，t)用于表示当前检测获取的二值化图像序列，在此次设计中，步态历史运动轨迹图像可表示为

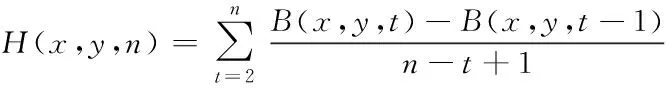
(1)

式中，n为轨迹点标准整数，t为运动时间。由此可见步态历史图像序列中每个像素数据均可以看做是当前目标点运动历史函数。而且越趋近于原始像素，其函数值越大。图像序列灰度的变化可以体现出当前步态运动方向[6]。步态历史图像的生成可以较好地将空间特征和时间信息体现在活动图像上，也就是在空间上较好地表达了当前步态活动的位置和区域，也可以在实践轨迹上描述当前步态运动的发生情况[7]。

根据上述建立的步态运动图像，图像序列中的运动行为就可以进行数据量化，用图像向量表示[8]。根据这一特性可对当前图像序列特征进行提取。目前常用的图像特征提取方法一般需要基于矩函数的特征向量[9]，这种方法不仅需要计算当前图像序列下的轮廓像素点，还需要计算当前形状的所有像素点。

对于像素点矩函数特征的识别，需选择Zernike矩作为识别方法[10]。对于当前计算机获取的数字图像，可以用积分用求代替，设p(x，y)是图像的基础序列，则结合式(1)得到历史运动轨迹图像序列特征提取结果为

(2)

其中x2+y2≤1，Vmn(x，y)为像素值多项式，m的取值范围为非0的正整数。Zermike矩的计算公式必须将图像中心进行平移，最终需要与向量数据的原点坐标重合，以此将图像像素点映射到单位圆内，完成特征向量数据提取。

2.2 基于低秩分解的结构化矩阵低秩表示模型构建

在图像序列的特征向量数据提取完毕后，当前步态活动图像序列已经完成了初步数据筛选，且所有数据格式均为向量格式时，还需充分考虑异常步态活动图像中数据所受的噪声因素，由此提高识别精度。导致传统识别方法识别精度较低的核心原因就是缺乏结构化的步态活动图像序列特征向量数据去噪过程。对此考虑，完成图像序列特征向量数据的去噪。

在矩阵低秩表示理论中，给定输入的步态活动图像特征矩阵F，它可以分解为以下两个部分：表示背景区域的低秩矩阵L和表示当前目标区域的稀疏矩阵S。在进行序列目标检测过程中，用于消解图像序列噪点，检测显著性目标矩阵的低秩表示模型可以转换为非凸优化问题。

假设当前输入图像x被划分为n个非重叠像素序列P={P1，P2，…Pn}。从每个图像序列中提取当前步态的特征维向量，xi∈R。则x可以有多个特征向量表示为F={x1，x2，…xn}。设计矩阵低秩表示模型，可以将当前的异步特征数据矩阵进行低秩分解，获取低秩矩阵L也就是当前图像的背景区域和稀疏矩阵S也就是当前异步显著目标。

因此通过最小化获取更小矩阵R的核范数，构建结构化矩阵低秩表示模型

D(z)=F(min(L)Pn+λS)

s.t.F=L+S

(3)

其中，S表示当前矩阵的核范数，λ为矩阵奇异值的和值。根据非结构化的稀疏诱导范数例对目标区域的稀疏矩阵S进行图像序列系数约束，将系数约束应用到结构化矩阵低秩表示模型中，充分完成了图像序列特征向量数据的去噪过程。

2.3 异常步态活动图像序列识别的实现

对去噪后的图像序列特征向量数据进行Curvelet特征转化，能够得到异常步态活动图像序列识别进行关键细节处理后的形变约束，根据形变约束可实现最终的图像序列识别。其具体步骤如下：

利用Curvelet算法选取出异常步态活动图像序列的待识别样本

(4)

其中，Svj为当前步态旋转角度信息，Vk为当前转换函数，ω为结构化系数，d为超像素对数，b为相邻超像素值的数据对集合。在数据转化过程中，需要填入当前步态空间数据位置在笛卡尔空间坐标中的系统描述，一般取值范围为u1>0，u2>p，p表示当前空间位置参数值。则经过Curvelet转换待识别样本公式如下

(5)

式中，DE(k，m，l)是Curvelet转换参数，E属于动态数据系数，k属于当前步态相关数据的权值参数。想要完成全步态动作的数据转换，则需要利用US转换和WS转换。

利用上述两种转换方式进行Curvelet特征转化可以用同一的描述模型，空间坐标相互关系均可以使用P(q2)表示，转换计算步骤的系数可以使用P(q2lnq)表示。这两种转换方法的区别在于US转换所包含的背景区域图像会存在步态转角的偏度，其可靠系数数值一般较大，而WS转换方式则不会出现角度偏转具体过程如下：

其次需要对全部步态数据相关数据值和图像坐标系统的分类量进行区域化处理，利用以下公式获取数值

g=δE(l)X(Vk，u，g)[q1，q2]

(6)

(7)

(8)

因为异常步态的不可避免会出现形变因素，上述利用Curvelet和2DPCA完成了数据的转换，将转换数据组成一个参数集合，{Yj，zj}表示，其中j=1，2，…，e，Yj是指在动态图像序列中，序列号是j图像的实际系数，如果zj的实际取值是1，那么代表该图像的序列为特征序列，反之则不是。根据3D渲染依靠数据系数排列可以划分为红色约束区域和绿色约束区域，制定特征数据，输入对当前数据进行图像的SVW处理，将步态关键点转换为坐标系统点，获取关键细节特征，理想平面图像的数据参数，其求解出的图像序列识别值如下

(9)

将上述参数作为图像数据的衡量标准，从而获取数据约束

zj=[X，γ(Yj)-c]-ψj>1

(10)

其中，ψ>0，j=1，2，…e，最终可以求出理想的异常步态活动图像序列识别函数如下

(11)

综上所述，通过实现当前异常步态活动图像序列的关键特点和去噪处理，即可提取点空间坐标参数内积，完成图像序列的识别。

3 实验结果分析

为了验证基于低秩分解的异常步态活动图像序列识别方法的有效性，进行仿真测试。在当前异常步态活动图像序列特征数据集MSR ACTION3D_0.1行为数据集上进行实验。该数据集共包括20种步态行为数据，每种行为数据均由5位表演者表演2次所取得平均值。为了保证序列数据识别的公平性，实验设置与文献中的数据方法完全相同，数据集中一般作为训练样本，一般作为测试样本。采用以往所最长用的超法向量特征参数作为参数设置，其中字典D中的数据值为100，正参数取值为0.17。图2给出了实验原始图像。根据图1所示的历史轨迹图像进行如下测试实验。

图1 原始历史轨迹图像

选取文献[3]方法、文献[4]方法与所提方法进行对比实验，测试方法的识别精度。图像序列特征向量数据的识别率直接影响识别精度，识别率越高，识别精度越高。经过实验，得到测试对比结果如图2所示：

图2 三种不同方法的识别率对比结果

根据图2数据可知，文献[3]方法的图像序列特征向量数据的识别率约为45%，最大识别率为58%；文献[4]方法的图像序列特征向量数据的识别率约为23%，最大识别率为35%；所提方法的图像序列特征向量数据的识别率约为90%，最大识别率为96%。对比实验结果得出，所提方法的识别率近乎是文献[3]方法和文献[4]方法识别率的一倍。充分说明所提方法的识别率更高，识别精度更高，具有优越性。

所提方法中基于Zermike矩的图像序列特征提取这一步骤，其提取准确度对整个方法的识别精度起到决定性的作用。为此，分别对文献[3]方法、文献[4]方法和所提方法的序列提取准确度进行测试，得到三种不同方法的对比结果如图3所示。

图3 三种不同方法序列提取准确度对比

根据图3中的数据可以分析出，采用文献[3]方法对图像序列进行提取，在第10次实验时出现最大提取准确度为58%，10次实验的平均序列提取准确度约为40%；采用文献[4]方法对图像序列进行提取，也是在第10次实验时出现最大提取准确度为61%，10次实验的平均序列提取准确度约为45%；采用所提方法对图像序列进行提取，依然是在第10次实验时出现最大提取准确度为80%，10次实验的平均序列提取准确度约为76%。对比三种不同方法的序列提取准确度可得出，所提方法的图像序列提取准确度远远高于文献[3]方法和文献[4]方法的序列提取准确度，说明所提方法的识别过程具有更准确地步骤基础，验证出所提方法的识别精度更高。这是由于本文方法在选取序列特征时，选择Zernike矩识别像素点矩函数特征，选择并提取图像序列有效特征，排除无效图像序列特征的干扰，一定程度上提升了序列数据提取的准确度。

所提方法构建的结构化矩阵低秩表示模型主要用于解决图像序列特征向量数据的噪声问题，以信噪比为测试指标，分别测试文献[3]方法、文献[4]方法和所提方法的去噪效果。得到对比结果如图4所示。

图4 三种不同方法的信噪比对比结果

分析图4结果得出，文献[3]方法和文献[4]方法在模型去噪的100s时间内，信噪比大幅度变化，从1dB低至0.05dB，在90s时再缓慢上升到1dB。所提方法的信噪比则较为稳定，只在40s到70s时，出现了一次1dB，整体上稳定在0.02dB。对比结果可看出，所提方法信噪比最稳定，去噪效果最理想。

4 结束语

基于低秩分解的异常步态活动图像序列识别方法，在经过仿真验证得出，其序列向量数据的识别率可高达90%，识别精度高，且去噪效果好。但未对所提方法的识别效率进行测试，接下来会对识别效率进行深入研究。