基于模型预测控制的直升机轨迹跟踪控制
高莘青,马 钊,梁颖茜
(航空工业西安飞行自动控制研究所,陕西 西安 710076)
1 引言
实现精准的直升机航迹跟踪在实际应用中具有重要的意义。然而,直升机气动特性复杂,各轴(俯仰、滚转、航向和总距)响应耦合严重,操纵较困难[1]。在该背景下,针对轨迹跟踪问题,近年来提出了众多的基于非线性理论的控制方法,包括滑模控制[2],自抗扰控制[3]、反步控制[4]等。大量仿真结果表明上述非线性控制方法能够保证良好的跟踪效果。然而,直升机的实际操纵对于系统状态以及操纵输入通常具有约束,而非线性控制理论难以同时考虑上述约束,对模型精度要求高,制约了其在工程实施的大规模推广应用。
模型预测控制(MPC)是工业控制领域应用广泛的多变量控制算法,并且占据了较大的市场份额[5]。模型预测控制的核心是滚动优化:在每个控制周期内,在已知当前系统状态以及输入的前提下,通过预测系统未来的状态并最小化优化目标,计算系统输入[5]。利用优化技术计算系统输入的显著优势在于,其能够融入系统状态以及输入的约束,而上述约束在实际应用中通常是需要考虑的关键问题。此外,MPC可通过凸优化求解,具有丰富的理论支撑。上述优点保证了MPC在工业界的广泛应用。
在飞行控制领域,MPC在轨迹跟踪领域进行了相关研究,可参考相关文献[6,7]。然而在实施中,需要关注以下关键问题。第一,计算代价。理论上,MPC算法可嵌入控制增稳层,也即通过MPC直接计算直升机的周期变距以及总距的控制量。对于工业控制,对象的动态特性比较缓慢,因此MPC的控制周期通常为5s~20s,而 MPC本身的计算代价在实施中并不需要太多关注。然而对于控制增稳回路,控制周期约为10ms,且飞控计算机算力有限,难以实时支撑MPC的在线优化。第二,直升机响应类型限制。理论研究通常忽视了各轴实际的响应类型,影响了MPC的实际可实施性。第三,在实际应用中需要合理地整定MPC参数,保证其对各轴响应类型动态不确定性具有一定的鲁棒性。
综上所述,本文主要工作总结如下。第一,提出了基于分层架构的MPC轨迹控制方法:底层控制增稳回路对直升机的速度以及姿态进行调节,而MPC架设在顶层的制导回路,通过对底层回路的姿态和速度指令进行调度,以期实现直升机轨迹的精确控制。与控制增稳回路相比,制导回路的动态特性更加缓慢,可采用更长的控制周期实施MPC,因此显著降低计算代价。第二,针对直升机典型的各轴响应类型,设计实用的MPC控制策略,确保各轴操纵符合预期。第三,针对实际对象的非线性特性,用了分段线性的方法,保证滚动优化的全局最优性。第四,针对响应动态的不确定性,采用了基于min-max原则的MPC参数整定法,保证了算法的鲁棒性以及在不同飞行条件下的可适用性。
2 直升机模型
本文考虑单旋翼以及带尾桨的直升机对象。根据欧美坐标系,直升机动力学方程、运动学方程和导航方程为

(1)

(2)

(3)
其中,VB=[VxVyVz]T为机体坐标系下机体线速度,Ω=[pqr]T为机体坐标系下机体角速度,Θ=[θφψ]T为欧拉角向量,P=[xy-h]T为北向、东向坐标和海拔高度,J为直升机的三轴转动惯量矩阵,Q为欧拉角向量与角速度向量直接的转换矩阵,TBE为从机体坐标系到地理坐标系的转换矩阵。FB与MB为机体坐标系下受到的由旋翼以及机体气动产生的力和力矩
FB=Fmr+Ftr+Ffus
MB=Mmr+Mtr+Mfus
(4)
其中,下标mr、tr、fus分别表示由主旋翼、尾桨和机体产生的力或力矩,详细的计算方式可参考文献[8]。直升机主要通过操控主旋翼总距、纵横向周期变距以及尾桨距,从而改变Fmr、Mmr、Ftr、Mtr,四轴操纵量分别为:纵向周期变距角θ1s,横向周期变距角θ1c,总桨距角θmr,尾桨桨距角θtr。
3 基于分层结构的MPC轨迹控制策略
3.1 轨迹控制基本架构
对于实际的工程应用,最通用的控制架构是基于时间分离尺度,自底向上依次构建分层次的姿态控制回路、速度控制回路和空间位置控制回路。本文将沿袭上述思路进行轨迹控制回路的搭建。需要注意的是,对于实际直升机控制,需要额外关注直升机的操纵响应类型[9]。由于直升机本身气动特性特点,飞控系统需要针对不同的飞行状态设计各轴响应类型。对于轨迹回路的设计,本文主要考虑表1所示的各轴响应类型,说明如下。

表1 直升机各轴操纵响应类型
俯仰通道:带速度保持的姿态控制响应类型(ACVH)。通过操纵改变机体俯仰角,并通过俯仰角的变化实现机体前向速度的控制。操控回中后,速度保持在当前值上。
滚转通道:带姿态保持的姿态控制响应类型(ACAH)。通过操纵控制滚转角,当操纵结束后,操纵回中,姿态回中。
航向通道:协调转弯模态(TC)。目标是在机体进行滚转动作时通过航向轴的控制实现侧滑的消除。
总距通道:垂速控制(Rate)。
上述响应类型是直升机在中高速下典型操纵响应类型:纵向操纵直接控制直升机前飞速度,横向操纵通过改变滚转控制直升机的偏航角速度,总距操纵直接控制直升机的爬升速度。根据上述的操纵类型,MPC控制架构如图1所示。MPC架设于顶层的制导回路,通过综合期望的直升机航迹、位置反馈信息以及对于实际操纵和直升机状态的约束,实时计算底层回路的前飞速度指令、滚转角指令以及垂速指令,最终实现直升机轨迹的精确控制。整套控制方案总结如下:通过调整前飞速度指令控制直升机飞行速度,调整滚转角指令控制直升机的航线方向,调整垂速指令控制直升机飞行高度,而航向通道与滚转通道进行交联,在直升机进行滚转机动时通过调整机头方向,实现侧滑的消除。需要注意的是,尽管直升机的操纵输入是4自由度,然而对于本文采用的MPC架构,MPC的输出仅有3自由度,并无航向通道。这是因为内回路航向通道的模态为协调转弯,其与滚转回路进行交联以实现侧滑的消除。
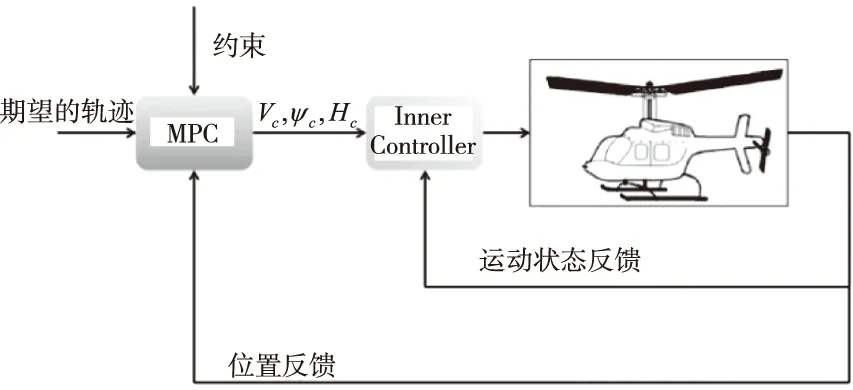
图1 MPC控制架构
3.2 工程可实施性分析
对于本文采用的控制策略,MPC并未在底层的控制增稳层实施,而是针对各轴实际响应类型,在顶层制导回路架设MPC控制器,通过对内回路指令进行调度,最终实现轨迹的精确控制。尽管MPC作为先进控制算法,理论上可以架设于直升机的控制增稳回路,但是从工程可实施性的角度,本文采取的控制架构具有如下优势。
第一,有效降低MPC实施的计算成本。直升机内部的控制增稳回路与直升机的稳定性和安全性密切相关,并且由于角速度和加速度响应的快速动态特性,因此需要较短的控制周期。在实际的工程应用中,控制周期在10ms左右。MPC尽管能保证良好的闭环效果,但其核心是优化问题,需要较高的计算代价,而实际飞控计算机算力有限,难以支持MPC的毫秒级的在线实时优化。对于顶层的制导回路而言,其涉及到的响应为速度响应和航向角响应。与角速度和加速度相比,速度响应与航向角响应的动态特性更加缓慢,响应时间通常为秒级。因此,0.1~0.5秒的控制周期通常可以保证制导回路的精准控制。与直接架设在控制增稳回路相比,计算代价至少可以降低90%。
第二,降低了对模型精度的苛刻要求。MPC需要对未来系统的状态进行预测,因此对模型的精度具有较高要求。直升机动力学具有高度非线性以及强耦合的特点,难以获取完全精确的模型。在底层通过合理的内回路设计,可以有效地对模型不确定性和耦合进行补偿。对于控制增稳回路的设计,PID控制以及模型跟随控制已经取得了成熟的工程应用[10]。对于本文采用的控制架构,MPC仅需要考虑各轴响应的动态,故建模难度以及模型不确定性将显著降低。以速度保持和姿态保持为例,内回路通常采用积分器,因此响应模型的增益为1,而响应的动态可基于飞行数据进行估计,因此有效降低了建模过程中的模型不确定性。事实上,闭环响应动态特性的估计是飞行品质评估的核心问题,在工程应用中已有较成熟的解决方案[11]。尽管在不同的飞行状态下各轴的响应特性具有一定的差异,仍然可以通过整定合理的MPC参数保证闭环控制的稳定性和鲁棒性。
4 基于模型预测控制的轨迹跟踪算法
4.1 MPC优化问题
考虑如下离散形式的系统模型
x(k+1)=Ax(k)+Buu(k)+Bdd(k)+Bww(k)
y(k+1)=Cx(k)+Ddd(k)+Dww(k)
(5)
其中:x(k)为系统状态向量,y(k)为系统输出,u(k)为系统输入,也称作操作变量,d(k)为干扰变量,其含义为可以测量但是无法直接控制的外扰,MPC通过前馈的机制对其进行补偿。w(k)为不可测的高斯噪声。
在每个控制周期,MPC通过上述系统模型对未来系统状态进行预测。定义x(k|k-1)为在k-1时刻通过系统模型对k时刻的状态预测值。在k时刻采集到系统实际状态,通过如下状态观测器对状态预测值进行修正

(6)
其中L为误差反馈矩阵,可采用Kalman滤波理论进行设计。对于预测步长p,系统状态可根据如下方程预测
X(k)=Γ0x(k|k)+H0u(k-1)+HΔuΔU(k)+HdD(k)
(7)
其中



未来时刻系统输出可根据式(8)进行预测
y(k+i|k)=Cx(k+i|k)+Ddd(k+i|k)
(8)
MPC通过以下带约束的优化问题计算计算系统输入[5]

(9)
其中,Y(k)为未来时刻系统输出预测y(k+i|k)所构成的数据向量,Yref(k)为期望的系统输出,正定矩阵Q和R为系统误差加权矩阵。优化目标为最小化跟踪误差,并同时保证系统输入的变化率尽可能平缓。此外,MPC优化考虑了系统输入和输出幅值以及变化率幅值的关键实际约束。
对于线性系统,MPC问题为凸优化问题,故ΔU(k)对于问题(9)而言是全局最优解。从长期的视角而言,如果模型是完全准确的,且全系统没有不可测干扰,则ΔU(k)可以保证是系统的最优输入。然而,由于模型的不确定性或者未知外扰的存在,则系统的预测和真实值存在差异。以长远的视角,ΔU(k)不能保证长时最优性。故在每一个控制周期内,MPC只实施ΔU(k)头m个分量,在第m个控制周期之后,通过滚动优化的方式,通过优化问题(9)重新计算系统输入ΔU(k)并实施前m个分量。通过式(6)状态观测器对系统误差的补偿以及滚动优化的形式,保证了MPC的可实施性。
4.2 分段线性MPC
针对第3.1节所述的直升机各轴响应类型,俯仰通道的响应为

(10)


(11)
垂直通道的响应为
+Gh(s)Vh_cmd(s)
(12)
对于MPC的实施,需要对上述传递函数进行离散化。对于直升机轨迹跟踪控制,以地面坐标系为参考。需要注意的是,因为直升机水平面(XY轴)的响应的参考系为机体系,故需要进行坐标转换:

(13)
其中Cθ、Sθ分别表示sinθ和cosθ,[VxVyVz]T和Vh分别为体轴速度和直升机垂直爬升率。

基于上述的MPC控制变量分配,对(13)进行线性化。对于直升机的机动,机体滚转角和俯仰角在幅值上具有限制,故在线性化的过程中认定SθSφ≈0。线性化的结果为
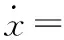
-SCVy-(SCC+SS)Vz

+(SSC-CS)Vz
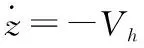
(14)
其中,上标“^”表示在当前控制周期内运动状态参数的测量值。
5 鲁棒MPC的设计
5.1 响应模型形式
基于实际直升机各轴内回路的实际特性,本文采用如下形式的响应模型

(15)
需要注意到,如果内回路的设计采用了积分器,可先验获取模型的稳态增益。在式(10)~(11)中的各轴响应模型中,对角元素的稳态增益为1,故模型参数应满足如下约束
Kz1z2=piω2
(16)
对于非对角元素可视为其它轴的操纵输入对本轴响应的干扰,而内回路的积分器可完全消除常值外部干扰,从而模型参数应满足约束
z1z2=0
(17)
5.2 MPC参数的鲁棒设计
内回路的三轴响应模型可利用飞行数据进行辨识,模型获取的难度相较直升机动力学模型显著降低。尽管如此,在实际的工程应用中模型仍然存在一定的不确定度。模型不确定性主要来源于两个方面:
1) 辨识误差。在进行飞行试验的过程中,由于测量噪声或者外扰的存在,导致所辨识的模型存在一定的误差。
2) 不同飞行条件下响应动态特性的差异,尤其是空速大小的影响较显著。
对于MPC参数的设计,需要考虑实际的模型不确定性。针对式(15)中的参数形式,本文考虑如下具有参数不确定性的模型:

(18)
需要注意,如果内回路采用了积分器,尽管模型具有两个零点,但是其不确定性仅仅只有1个自由度,因为零点必须满足约束(16)或者(17)。
影响MPC性能的关键参数总结如下:预测步长p、控制步长m、模型输入输出权重矩阵Q和R。上述参数通过如下基于min-max准则的优化问题进行优化[12]

(19)
上述优化问题是双层优化问题。内层优化变量是响应模型的参数,其目标是对于给定的MPC参数,搜索最坏的控制效果;外层优化变量是MPC参数,其目标是确定最优参数,以保证对于所有可能的响应模型,使得MPC在最坏情况下的控制误差是最小的,也即最小化最坏情况下的控制误差。
6 仿真验证
本节通过数值仿真对提出方法的有效性进行验证。期望的直升机跟踪轨迹采用螺旋上升曲线
xref(t)=350sin(2πt/250)+150
yref(t)=350cos(2πt/250)
zref(t)=0.5t
(20)
基于直升机内回路的设计,三轴的指令与响应直接的动态关系见表2。直升机的初始位置坐标为(0,0,0),偏航角为0rad。基于对各轴内回路动态特性分析,MPC的控制周期设为0.25s。

表2 直升机3轴指令模型
其中,G11(s)~G33(s)传递函数为
根据实际直升机的操纵需求,各轴指令应满足如下约束
-3m/s≤Vx_cmd≤15m/s
|ΔVx_cmd|≤0.6m/s
-1.5m/s≤Vh_cmd≤3m/s
|ΔVh_cmd|≤0.5m/s
(21)
其中,Δ表示变量在相邻控制周期内的变化量。在确定上述操纵变量的约束后,通过离线优化,预测步长p设置为15,控制步长m设置为1,输入输出权重矩阵Q和R分别为diag[1,1,1]和diag[0.115,0.115],其中符号diag表示对角矩阵。
尽管MPC的控制周期为0.25秒,远远高于控制增稳回路的控制周期(10ms),但是其仍然能够保证精准的航迹跟踪效果。MPC操纵变量的求解本质上为凸优化问题,基于已有的快速凸优化技术,在0.25秒内足够控制步长的求解。
图2~4展示了3轴的航迹跟踪结果。由于直升机纵横的耦合作用,水平面的跟踪效果与高度轴相比稍差,然而仍然在合理的水平:跟踪误差在50秒左右快速收敛到合理的水平,在100秒之后误差收敛至1.5米以内。

图2 X轴轨迹跟踪结果

图3 Y轴轨迹跟踪结果

图4 高度轴轨迹跟踪结果
图5展示了3维平面的轨迹跟踪控制结果:直升机的实际轨迹能够快速跟踪参考轨迹,而跟踪误差也能快速收敛。上述结果验证了基于MPC的轨迹控制方法的合理性。

图5 3维度轨迹跟踪结果
7 结论
本文提出了基于MPC的直升机轨迹跟踪控制方法。在工程应用中,直升机具有特定的各轴响应类型。针对实际响应类型的约束,本文提出了基于制导层指令调度的MPC控制架构。一方面,该架构保证了针对不同响应类型的可扩展性,另一方面也能够确保MPC以更合理的控制周期进行解算,显著降低了计算成本,保证了工程可实施性。基于分段线性MPC的控制策略扩展了方法对实际非线性过程的适用性。针对实际工程应用中的模型不确定性,采用了依据min-max准则的MPC设计方法,提高了方法的鲁棒性。仿真案例验证对方法的有效性与合理性进行了验证,结果表明方法控制精度和计算代价合理,具有工程推广前景。

