航速和力对潜艇垂直面运动影响仿真分析
胡 坤,何 斌,张建华,杨国栋
(海军潜艇学院,山东 青岛 266199)
1 引言
潜艇垂直面运动指的是只改变或保持纵倾和深度而不改变航向的潜艇运动。相对于水平面的航向控制来说,潜艇在垂直面内能够安全航行的水深大约只有潜艇艇长的3到5倍左右,既不能超出极限深度,也不能不适时宜地浮出水面。由于现代潜艇的高航速、大潜深特点,潜艇的运动幅度大,特别是潜艇在水下航行一旦由于战斗破损、操纵失误以及海水比重突然变小等原因使潜艇突然出现较大的负浮力时,若无法及时运用堵、封、排等措施限制进水往往会造成严重的危险纵倾掉深险情[1]。因此,垂直面的深度与纵倾控制对潜艇操纵来说更为重要。
潜艇在垂直面改变深度的方法有两种[2]:一种是通过浮力调整水舱的注排水或首尾纵倾平衡水舱间的调水造成浮力差、力矩差等静力方法,使潜艇潜浮或同时形成纵倾,再用车变深。第二种也是最常用的方法时是操艏艉升降舵使潜艇做有纵倾或无纵倾变深运动。无论是浮力调整水舱水舱的注排水还是操纵升降舵,归根结底都是在航行中的潜艇上施加了垂直方向的外力(矩)。因此,研究航行中的潜艇在垂直面外(矩)作用下的运动特性显得尤为关键。本文以模型潜艇为研究对象,基于潜艇垂直面操纵运动方程,通过理论推导和仿真验证,分析了不同航速的潜艇在静力和升降舵舵力作用下的运动特性以及艏艉升降舵的操纵特性。
2 潜艇垂直面运动方程
2.1 潜艇垂直面操纵非线性方程
潜艇在垂直面中的航行机动与水平面运动虽然有类似的地方,但是由于引入了重力等静力,因此其操纵特点与水平面还是有显著差异的地方(例如,垂直面不可能出现像水平面那样的360°旋回现象等)。潜艇在垂直面运动时,除了受到流体动力作用外,还受到重力、浮力、扶正力矩等静力(矩)的作用,这些静力(矩)会对潜艇的垂直面运动产生重要影响。文献[3]详细推导了潜艇垂直面操纵运动非线性方程式,形式如下
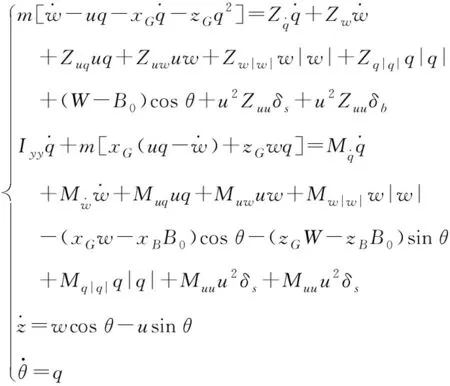
(1)
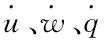
如果给定潜艇质量、转动惯量以及相关的水动力系数便可以采用(1)式对潜艇垂直面的操纵运动进行相关的数值仿真[4]。
2.2 潜艇垂直面操纵线性方程
当潜艇在垂直面内作弱机动时,运动参数Δu、w、q、δb、δs均为小量,计及剩余静载P、Mp和扶正力矩Mθθ,便可以将潜艇垂直面操纵非线性方程简化为潜艇垂直面操纵线性方程
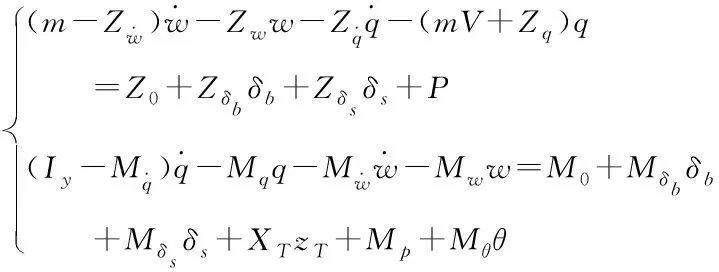
(2)
潜艇在实际垂直面航行中的操纵表明,绝大多数情况下潜艇的纵倾、垂速等关键运动参数的变化都不打,特别是对产生艇体水动力有重要影响的冲角在变深机动时大约只有1°~3°左右,超过4°的情况很少出现,纵倾角受到安全性的要求,通常也在7°~10°以内。大量的理论数值计算也表明,潜艇垂直面操纵运动方程中的相关非线性对潜艇的实际航行机动影响很小。因此,采用垂直面线性方程与非线性方程在解算潜艇垂直面运动的数值解几乎没有差别。
文献[5]采用仿真技术具体分析了潜艇垂直面线性与非线性方程的数值解的误差,得出的结论是线性方程与非线性方程的最大数值误差均在10%以内。由于解算线性方程的速度要比解非线性方程快得多,并且线性方程中的各个参数物理意义也非常容易理解,因此垂直面操纵运动线性方程对于潜艇操纵理论分析有很高的实用价值。由垂直面操纵线性方程退化的俯仰定常运动方程是研究潜艇行进间均衡、保持定深直航、计算承载负浮力和分析垂直面机动特征量的基础。因此,本文的理论研究与仿真分析均是基于形如式(2)的潜艇垂直面操纵线性方程。
3 潜艇在静力作用下运动特性的理论分析
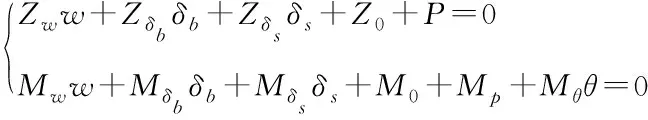
(3)
潜艇在水下运动的大多数情况下,如航渡、巡逻、阵地待机、使用武器(鱼雷攻击、发射导弹等)时,都处于或接近于无纵倾等速直线定深运动。当潜艇以一定航速作定深直航时,若受到外力P(不失一般性,假设外力P的方向是向下的)的持续作用,在经过一段非定常运动后,最终将进入新的定常直线潜浮运动。相对于原等速定深直航运动来讲,潜艇在新增加的外力作用下的运动参数应满足以下平衡方程[3]
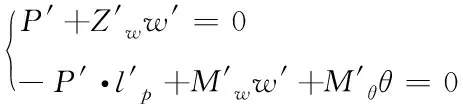
(4)
上式中已经对各个参数进行了无因次化,并有以下两点说明:
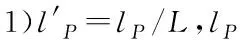
2)Z′w、M′w分别是潜艇有冲角艇体水动力系数和有冲角艇体水动力矩系数,对艇型一定的潜艇来说均为常数。
3)M′θ比较特殊,它与航速的平方成反比,其表达形式为:M′θ=-m′gh/V2。
通过式(4)可以进而求解得到冲角α和纵倾角θ的表达形式,即
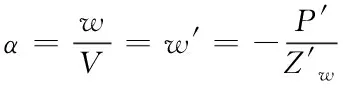
(5)

(6)
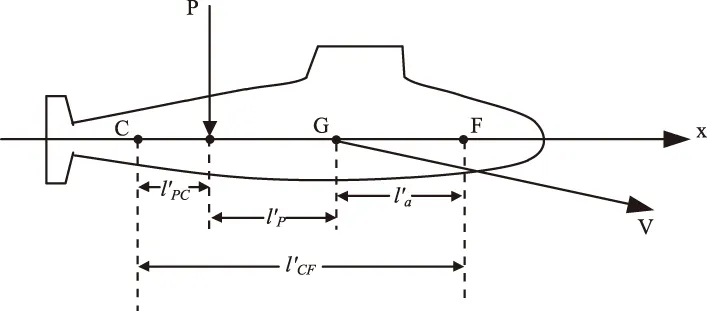
图1 潜艇垂直面力臂
由于潜艇垂直面运动时,潜浮角的大小等于纵倾角与冲角的差值(χ=θ-α),因此有了冲角α和纵倾角θ的表达式,便不难推导出潜浮角χ的表达式
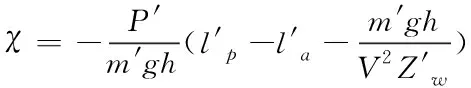
(7)
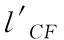
因此,潜浮角的表达式可进一步简化为
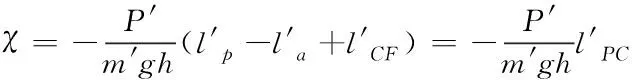
(8)
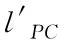
1)若外力作用在F点之前,最终使潜艇埋首下潜;
2)若外力正好作用在F点上,最终使潜艇无纵倾下潜;
3)若外力作用在F点之后。将引起抬首。潜艇是下潜或上浮取决于载荷作用点P与潜浮点C的相对位置:当航速高,C点向首移动,以致C点位于P点之前。此时将引起抬首上浮;当航速低,C点向尾移动,以致C点位于P点之后。此时将引起抬首下潜。
4 数值仿真分析
由于潜艇垂直面操纵线性方程形式简洁,解算速度快,并且与非线性方程的数值解非常接近,因此本文采用垂直面操纵运动线性方程式(2),以模型潜艇为研究对象,利用C#语言编制潜艇垂直面仿真运动软件[6][7]。通过仿真计算进一步分析不同的航速以及外力作用点的差异对潜艇垂直面操纵运动特性的影响。
4.1 航速对潜艇运动特性的影响
当潜艇受到的外力一定时,通过上节的分析可知,随着航速的不同,会引起潜浮点C在潜艇纵轴方向上的移动,导致外力的作用点与潜浮点C之间的距离发生变化,进而影响到最终的潜浮状态。
表1为不同航速时,力臂lC(也就是C点的纵向坐标值)的计算值。从表1可以看出,低速时(小于4kn)潜浮点在重心之后,随着航速的增大,潜浮点逐渐前移,到18kn时,已经移动至重心之前16.5m处。潜浮点随航速向前移动的极限是F点,也就是说当航速趋近于无穷大时,lCG的极值为17.36m。
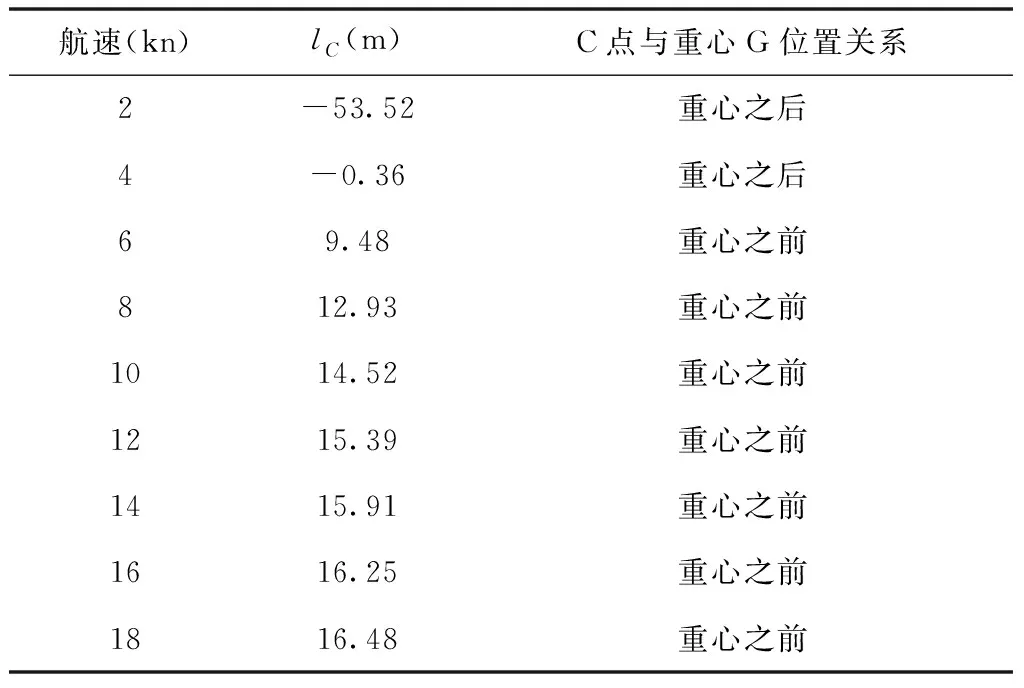
表1 不同航速时的潜浮点坐标值
不失一般性,假设潜艇水下均衡完毕保持无纵倾定深航行,浮力调整水舱注水10t(相当于在潜艇重心处施加一个向下的10t的力P),图2为航速分别为2kn、4kn、6kn和8kn时,在力的作用下的运动响应。
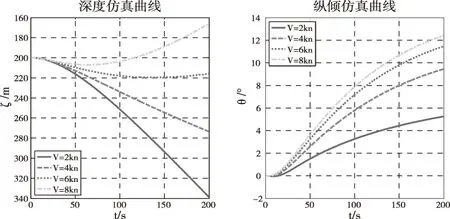
图2 深度及纵倾响应
通过深度及纵倾响应仿真结果可以看出,不同航速时,潜艇在给定外力下的运动响应有很大不同。当航速较小时,潜浮点C位于重心之后,潜艇在这个向下的力的作用下最终做下潜运动(见V=2kn、V=4kn时的仿真曲线);当航速较大时,C点逐渐前移至重心之前,潜艇在这个向下的力的作用下最终做上浮运动(见V=6kn、V=8kn时的仿真曲线)。需要指出的是,由于潜艇的水动力中心点F是一个定值,因此无论航速高低,潜艇在这个力P的作用下的纵倾的符号是一定的,从图中可以看出,潜艇均呈现尾倾状态。也就是说,航速较低时,潜艇最终做尾倾下潜运动,航速较高时,潜艇最终做尾倾上浮运动。
当潜浮点C与重心重合时,在重心上施加的力只造成潜艇的纵倾,而不引起深度的改变,令χ=0,由(7)式求得对应的航速为
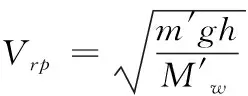
(9)
该航速称之为作用点位于潜艇重心处的静力逆速,带入模型潜艇的相关数据,可以解算出作用点位于潜艇重心处的静力逆速为4.04kn。也就是说当航速等于4.04kn时,潜浮点C与重心G重合,潜艇在作用点位于潜艇重心处的静力的作用下,最终将做定深航行;当航速小于4.04kn时,潜浮点C位于重心之后,潜艇在作用点位于潜艇重心处的静力的作用下,最终将做下潜运动;当航速大于4.04kn时,潜浮点C位于重心之前,潜艇在作用点位于潜艇重心处的静力的作用下,最终将做上浮运动。这与表1的计算结果及图1的仿真结果是一致的。
作为一个特例,如当潜艇突然进入密度较小的海域,相当于在浮心上(此时lp=0)受到一个负浮力作用,此时潜艇最终的潜浮状态显然与当时的艇速有关。低速时,潜艇将在负浮力作用下抬首下潜,高速时,此负浮力最终将使潜艇抬首上浮。
4.2 力的作用点位置对潜艇运动特性的影响
当潜艇航速和受到的静力大小一定时,随着静力作用点的不同,潜艇也会呈现出不同的运动特性。由表1可知,6kn航速下,lC=9.48m,也就是说潜浮点C位于重心之前9.48m。同时由lα的计算公式可以解算出lα=17.36m,即水动力中心点F位于重心之前17.36米。假设有一个向下的力P作用在潜艇上,以下针对三种不同情况展开进行讨论:
1)若力的作用点位于潜浮点C之后,不失一般性,假设该力作用在重心上,如图3所示。

图3 外力作用点在C点之后
通过前面的分析可知,由于P的作用点在潜浮点C之后,也在水动力重心F点之后,因此解算出来的潜艇的纵倾角和潜浮角均为正值。下图为模型潜艇水下均衡完毕,以6kn航速保持无纵倾定深航行,在lp=0处施加一个大小为10t的力后,潜艇的深度及纵倾响应曲线,可以看出,在外力的作用下,潜艇最终会做尾倾上浮运动,这与第三节的理论分析结果是一致的。
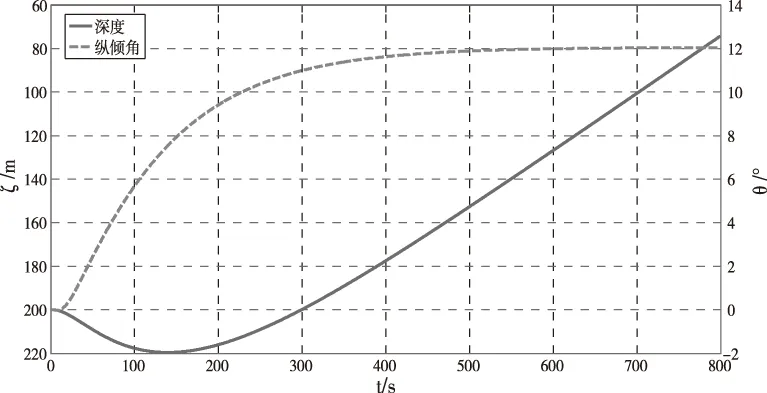
图4 V=6kn,lp=0,深度及纵倾响应
2)若外力的作用点位于潜浮点C和水动力中心点F之间,如图5所示。
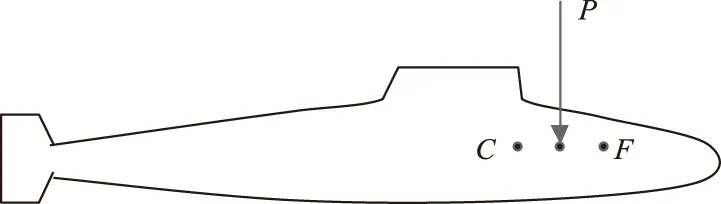
图5 外力作用点在C点和F点之间
由于P的作用点在潜浮点C和水动力中心点F之间,也就是说在C点之前,F点之后,因此解算出来的潜艇的纵倾角为正值,潜浮角为负值。图6为模型潜艇水下均衡完毕,以6kn航速保持无纵倾定深航行,在lp=12m处施加一个大小为10t的力后,潜艇的深度及纵倾响应曲线,可以看出,在外力的作用下,潜艇最终会做尾倾下潜运动。
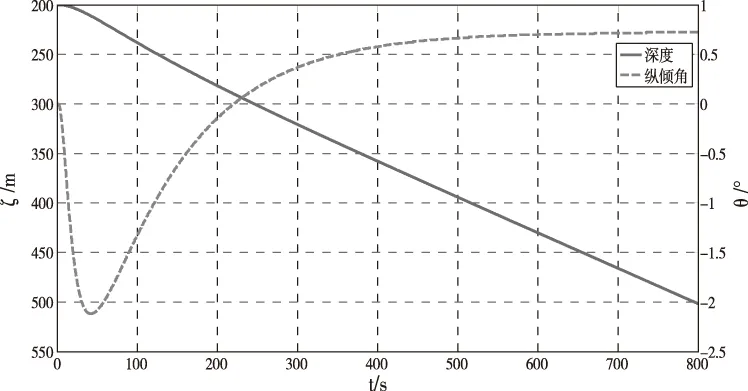
图6 V=6kn,lp=10,深度及纵倾响应
3)若外力的作用点位于水动力中心点F之前,通过前面的理论分析可知,潜浮点C一定在水动力中心点之后,因此这时外力的作用点也一定在潜浮点C之前,如图7所示。

图7 外力作用点在F点之前
由于P的作用点在潜浮点C和水动力中心点F之前,因此解算出来的潜艇的纵倾角为负值,潜浮角也为负值。图8为模型潜艇水下均衡完毕,以6kn航速保持无纵倾定深航行,在lp=20处施加一个大小为10t的力后,潜艇的深度及纵倾响应曲线,可以看出,在外力的作用下,潜艇最终会做首倾下潜运动。

图8 V=6kn,lp=20,深度及纵倾响应
4.3 艉舵逆速
潜艇在水下航行时,为了争取时间攻击敌人或规避敌人的攻击,均要求潜艇能迅速地、准确地改变深度。而通过操纵升降舵改变深度,简便、迅速,又易控制,所以是最基本的变深方式。当操纵升降舵时,相当于在升降舵的舵板中心处施加了一个外力,在这个外力作用下潜艇将产生新的艇体水动力和艇体水动力矩,并进一步改变深度和姿态[3][8]。
现代潜艇有一般布置有艏、艉两个升降舵,其中艏升降舵一般布置在水动力中心点之前,因此,无论航速高低,艏升降舵的操纵特性是不变的,操艏上浮舵潜艇最终会做尾倾上浮运动,操艏下潜舵潜艇最终会做首倾下潜运动。而艉升降舵布置在靠近潜艇艇尾处,故一定会存在一个航速,使得在这个航速下,通过式(6)解算出的潜浮角χ=0,相当于在这个航速下潜浮点C移动到了艉舵舵板中心点。在这个航速下,艉升降舵的任何转舵都不能改变潜艇的潜浮角(即不能变深),因此这个航速称为艉舵逆速,记作Vrs。通过前面分析可知,随着航速的降低潜浮点C逐渐向艇尾移动,又由于艉升降舵靠近艇尾,所以艉舵逆速均处于低速区。通过潜艇垂直面线性操纵方程可以推导得出艉舵逆速公式,其表达形式如下
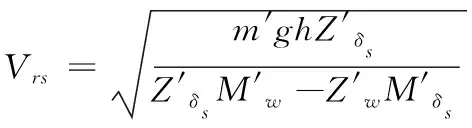
(10)
对于本文的模型潜艇来说,将相关水动力系数等参数代入式(9)可以解算出艉舵逆速在2.3kn左右。当潜艇航速高于艉舵逆速时,潜浮点C位于艉舵作用点之前,这时艉升降舵将呈现正常操纵性。图9为行进间均衡好的潜艇以6kn航速保持无纵倾定深航行,艉升降舵操下潜舵10°舵角后,潜艇垂直面深度及纵倾相应仿真曲线。
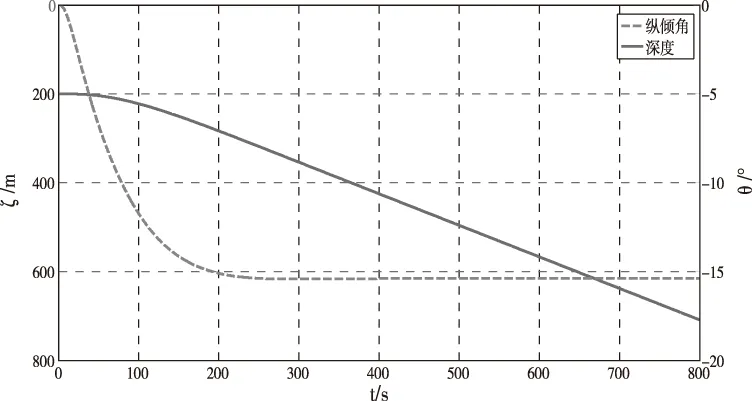
图9 V=6kn,δs=10°,深度及纵倾响应
通过仿真可以看出,当航速大于艉舵逆速时,操纵艉下潜舵,经过一段历时较短的过渡过程后,潜艇最终做首倾下潜运动,这时艉升降舵呈现正常操纵性。
当潜艇航速低于艉舵逆速时,潜浮点C位于艉舵作用点之前后,这时艉升降舵将呈现反操纵性。图10为行进间均衡好的潜艇以2kn航速保持无纵倾定深航行,艉升降舵操下潜舵10°舵角后,潜艇垂直面深度及纵倾相应仿真曲线。
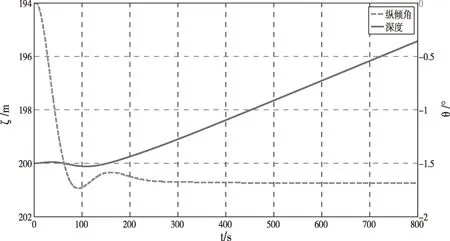
图10 V=2kn,δs=10°,深度及纵倾响应
可以看出,当航速小于艉舵逆速时,操纵艉下潜舵,经过一段历时较短的过渡过程后,潜艇最终做首倾上浮运动,操下潜舵潜艇反而会做上浮运动,说明在这个航速下艉升降舵呈现出反操纵性。因此在低速时操纵艉升降舵应特别注意这一现象。
5 结束语
本文针对航速和力对潜艇垂直面操纵运动的作用,比较分析了了潜艇垂直面线性操纵运动方程和非线性操纵运动方程。以线性方程为基础,对潜艇在静力作用下运动特性进行了理论分析。以模型潜艇为研究对象,基于潜艇垂直面线性操纵运动方程,仿真分析了不同航速、不同力的作用点的条件下潜艇垂直面深度及纵倾变化规律。潜艇在外力作用下的深度变化规律与潜浮点和外力作用点的前后关系密切相关,而纵倾变化规律由水动力中心点和外力作用点的前后关系确定。进而分析了艉舵逆速存在的条件以及艉舵在不同航速条件下的操纵特性。仿真结果表明,航速对潜艇的操纵特性有着重要的影响,作用在潜艇上的外力一定时,在不同的航速条件下潜艇会呈现出完全不同的运动特性。最后需要指出的时,本文研究的潜艇在外力作用下运动规律,均为经过短暂过渡过程后潜艇处于定常运动时的运动特性。

