基于毗域动力学的机身蒙皮疲劳裂纹仿真
王杰铖,常锦才,祝青钰
(1. 华北理工大学理学院,河北 唐山 063210;2. 中国航空综合技术研究所,北京 100028)
1 引言
多部位损伤(MSD,Multiple Site Damage)问题[1]的提出起源于Aloha事故,多裂纹的连通造成了蒙皮结构的破坏。此后,人们发现该问题普遍存在于飞机、火车[2]、桥梁[3]等工程结构中。疲劳裂纹的存在削弱了结构损伤容限特性[4],严重影响了其使用寿命。因此,需要精确的结构健康检测技术来对结构演变趋势进行预测分析,以保证结构在设计寿命内的安全性和可靠性,并节约成本。目前,结构损伤模型问题使用最为广泛的方法是有限元方法(FEM, Finite Element Method)。隋立军等[5]通过试验对机身蒙皮试件进行了有限元分析,结果表明了多裂纹的共同作用造成了裂纹扩展速率的增加。学者们在常规有限元方法的基础上提出了它的改进算法扩展有限元法(XFEM, Extended Finite Element Method),解决了二次网格划分问题,节约了计算时间。谢俊杰等[6]利用扩展有限元对滚动轴承内部裂纹扩展问题进行了模拟仿真,计算出裂纹扩展释放的能量;王综轶等[7]将扩展有限元法应用于交通信号支撑结构的疲劳寿命预测。这些表征裂纹演变的方法基于物体是连续体这一基本假设,仿真过程对网格具有较强的依赖性。
为实现多部位损伤的机身蒙皮结构裂纹演化仿真,采用毗域动力学方法(PD,Peridynamics)建立疲劳裂纹演化运动方程。该方法摒弃了物体的连续性假设,以离散晶格间的相互作用力形式对宏观不连续现象进行了重新定义,物体在形变过程中仅需满足柯西四个基本假设中的能量守恒律,以积分方程的形式来描述选定区域内材料的断裂情况,避免了导数在不连续处不存在的奇异性。
2 疲劳裂纹仿真原理
毗域动力学最早由Silling提出并得到推广[8,9],而后引发了国内学者[10-12]的关注。该方法适用于处理复杂物理模型的建立问题。本质上是对连续性的一种非局部新定义,从微观角度以积分形式表征宏观连续现象,避免了在裂纹处求导的困难。
2.1 模型建立
局部思想的裂纹运动方程以Hamilton算子来表征:
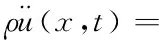
上式的求解需要对应力张量求偏导,在面对复杂物理模型时,方程难以求解。在处理此问题时,以粒子间的相互作用力为出发点,从微观角度对裂纹进行了重新定义,认为结构上任一点x与该点所视范围δ内的所有物质点均存在相互作用力,这些完整的力键构成了宏观意义H上的连续,如图1所示。

图1 物质点间的非局部作用
通过对物质点做效果叠加,将裂纹处梯度方程转换成如下积分运动方程
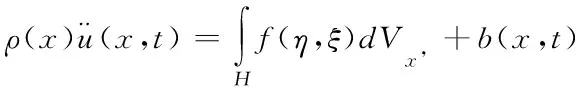
(1)

对于弹性材料,点对相互作用f可以由点对间的弹性势能推出
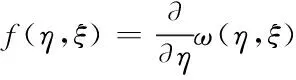
(2)
若材料的拉伸与点对间的弹性势能呈线性变化趋势,则
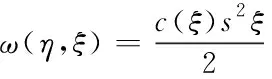
(3)
式中,c(ξ)为微模量函数,表示的是材料点对间键的弹性刚度,s是键的伸长量

(4)
通过对式(4)积分可以得到毗域范围内点对的材料断裂能W

(5)
假设微模量函数c(ξ)=c0是常数,由式(5)与载荷所做的功联立可得
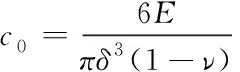
(6)
式中E是材料的杨氏模量,ν是泊松比。
毗域动力学理论中引入了损伤的概念,用于判断点对间的相互作用效果,当超过了键的临界伸长量s0,则点对间不再存在相互作用,即产生裂纹。对于二维案例,有

(7)
将式(3)和式(4)带入式(2),并联立式(7)可得点对相互作用力f

(8)
2.2 模型离散化
根据PD理论将机身蒙皮结构离散成晶格的思想,式(1)可转换成求解有限和的形式
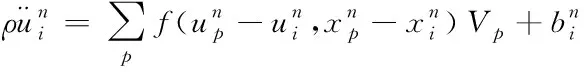
(9)
式中n为时间步长,Vp为节点p处的体积,下表为节点号。
对于线性化模型,有

(10)
左边的加速度场表示为
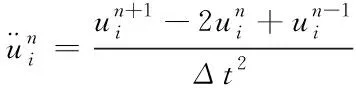
(11)
在式(10)中,为保证方程求解的稳定性,令

(12)
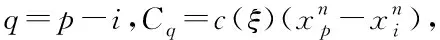
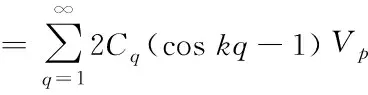
(13)
定义

(14)
用式(14)代入(13)求解ξ可得

(15)
由于|ξ|≤1,有

(16)
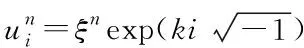

(17)
因此
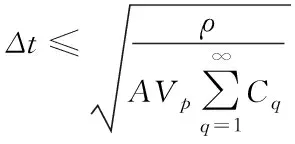
(18)
更加普遍的形式为
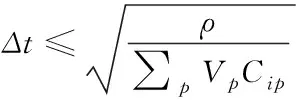
(19)
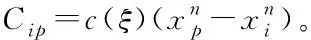
3 仿真实验
3.1 基于毗域动力学的裂纹演化模拟
以二维含孔机身蒙皮结构为研究对象,假定蒙皮结构是均匀,各向同性的弹脆性材料,蒙皮结构其杨氏模量为192GPa,泊松比为0.3,密度为8000kg/m3,尺寸为长50mm,宽50mm,孔直径10mm,毗域半径为δ=3.015Δx,晶格常数Δx为0.5mm,临界伸长量s0为0.02,节点体积为ΔV=1.25×10-10m3,时间步长Δt=1.0s,时间步数为1000。通过毗域动力学方法模拟裂纹演化结果如图2所示。


图2 基于PD的单孔裂纹模拟
如图2所示,分别对单孔边裂纹扩展的四个时间步长进行了可视化模拟,在时间步长为675时,孔边裂纹开始产生,随着步长的增加,裂纹开始扩展,直至时间步长为1000时,整个机身蒙皮结构破裂。
现行的损伤容限技术考虑的仅是单一裂纹情况,没有考虑多裂纹的存在,多裂纹连续扩展会产生干涉效应,导致裂纹扩展速率加快、临界裂纹尺寸减少等现象。因此,多裂纹对工程结构造成的危害远大于单一裂纹,多裂纹结构剩余寿命预测方法的研究迫在眉睫。针对该问题,采用PD方法对双孔孔边裂纹的演化过程进行模拟,结果如图3所示。
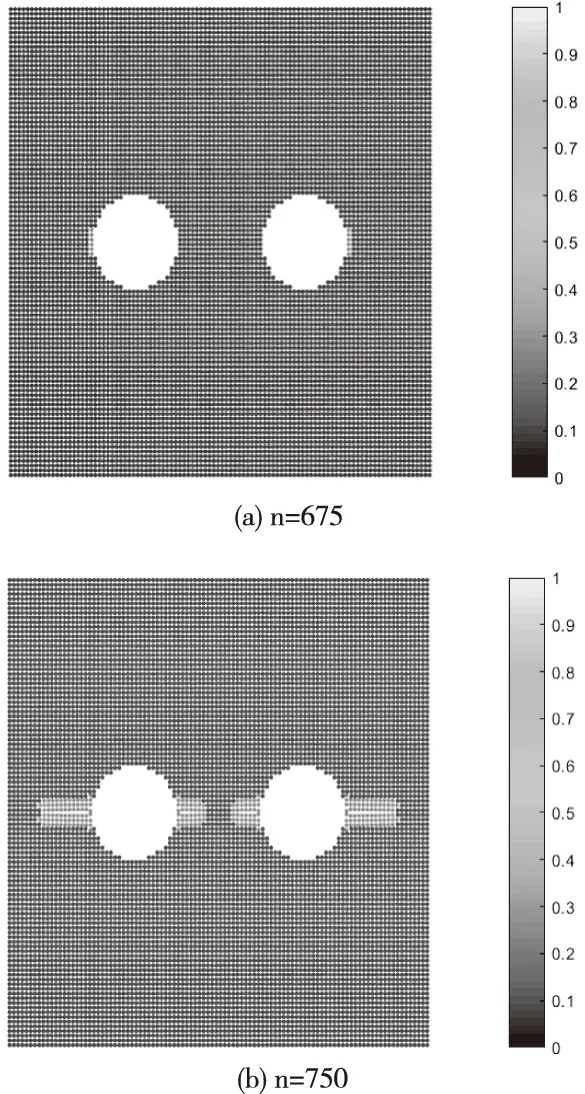

图3 基于PD的双孔裂纹模拟
通过图3双孔孔边裂纹演化的模拟可知,在时间步长为675时,双孔孔边外侧裂纹开始萌生,在时间步长为750时,双孔内侧裂纹扩展长度小于外侧,在时间步长为825时,双孔之间的裂纹已经联通,整个结构就已基本破裂。验证了在多裂纹存在的情况下,由于干涉效应的存在,导致了裂纹扩展速率的加快,加速了机身蒙皮结构的破裂。
上述仿真基于理想状态下进行,离散化的每个粒子在受外力情况下具有相同的初速度,产生了对称的疲劳裂纹。在通过MTS Landmark电液伺服疲劳试验机系统对多种金属结构进行疲劳裂纹试验中发现,裂纹的开口位置和扩展方向通常不具有对称性。如图4-图6所示。

图4 MTS Landmark电液伺服疲劳试验机系统

图5 机身蒙皮结构

图6 7050铝合金HST645-6高锁栓连接件
实际疲劳试验中,对物体施加外载荷,离散粒子的运动状态可以视为流体运动,在运动过程中存在层流现象,各层粒子以不同的速度向前运动,影响疲劳裂纹的扩展速度和方向。根据牛顿粘性定律对离散模型粒子的初始速度进行了修正,速度分布呈抛物线,其仿真结果如图7所示。
如图7所示,在时间步长为675时,由于离散粒子初始速度的降低,孔边疲劳裂纹并没有产生,表明疲劳裂纹的萌生时间延后了,在时间步为750时,右侧孔边裂纹开始萌发并扩展,时间步为825时,双孔的疲劳裂纹都已经产生,时间步为1000时,双孔的疲劳裂纹连通。根据该仿真结果与实际的疲劳裂纹图片对比可见,两者之间具有较高的相符度,证明了该方法在处理疲劳裂纹演化问题的优势。

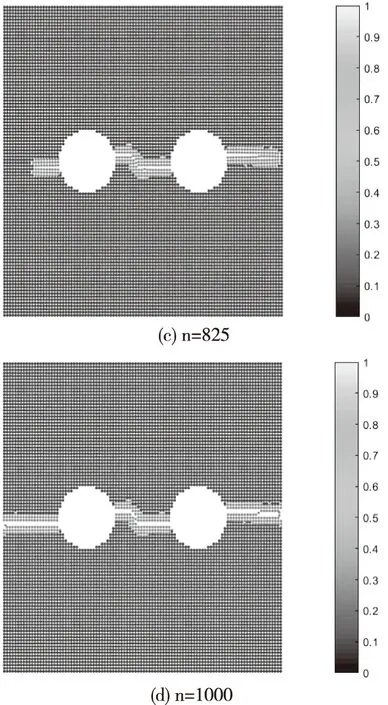
图7 基于PD的修正双孔裂纹模拟
3.2 基于扩展有限元方法的裂纹扩展模拟
采用传统方法中的扩展有限元方法对裂纹演化进行了模拟,其结果如图8所示:


图8 基于XFEM的单孔裂纹模拟
通过上图可知,扩展有限元法可以用于单孔裂纹演化过程的模拟,但是其仍需进行网格划分,对网格具有较强的依赖性,且该方法基于连续性假设,并不能很好地解释应力尖端的奇异性,自然也不能考虑尖端应力强度因子之间的干涉作用。因此,该方法在双孔裂纹演化模拟上的应用有待进一步研究。
4 结论与展望
毗域动力学方法提供了一种积分的思想,从非局部的观点来重新定义裂缝的萌生,生长和扩展,较好地解释了应力尖端的奇异性,对裂纹路径形状、分支模式和传播速度有较好的预测能力,解决了连续介质力学在遇到含裂纹的材料时,方程求解困难的问题。该方法摒弃了物体变形时仍保持连续性的基本假设,对连续性进行了非局部新定义,以微观粒子间作用力的表现形式将局部和非局部思想统一在一个体系下。相较于有限元方法,其数值求解过程是一种无网格法,能较好地自发模拟裂纹演变过程。本文建立了航空连接结构裂纹演变问题的非局部模型,结合实际疲劳试验对PD模型进行了修正,并将毗域动力学方法与扩展有限元方法进行了对比,算例表现了毗域动力学方法在处理不连续区域时的优势,避免了有限元法的网格依赖性,从微观粒子角度解释了应力尖端的奇异性,与实际疲劳试验具有较高的相符度。该方法可应用于航空故障诊断与预测,将可推广应用在缺陷、相变、位错等其它需要考虑材料内部作用的复杂问题,为非局部问题提供新的解决方法。非均匀材料的离散化问题有待进一步研究。

