深度建构分数认知，循着逻辑学会思维——以三上《分数的初步认识》一课的教学为例

李晓飞

数学教学必须超越具体知识和技能深入到思维层面，由具体方法和策略过渡到一般性的思维策略与思维品质的提升，由教师指导下进行学习逐步转变为学会学习。只有从数学知识的逻辑结构切入，以宏观的知识体系观照每个知识点的价值，依循知识点的内部逻辑结构，找准学生的经验起点和延伸点，合理设计课堂教学，让学生经历操作（手脑）探究、总结反思等再认识思维活动，寻求、体会并主动缔结知识的内在联系，建立起个性鲜明的结构性认识，才能帮助学生完整地经历由浅入深、由一般到具体的思维过程，真正学会学习。

从整体结构来看，苏教版三上《分数的初步认识》一课是对数概念的扩展，是典型的“种子课”。教师教学时需要让学生结合具体情境理解几分之一，感知分数能表示部分和整体之间的关系，也能表示具体数量，体会平均分在分数中的特定价值，能比较几分之一的大小，为后续相关内容的学习做好孕伏。教学应从经验出发，依循知识结构组织教学内容，促使学生主动加工数学活动经验，通过再创造生成深层认知，学会数学地思维。

一、生活→数学：超越技能进入思维层面

由学生熟悉的情境引入教学，基于学生在生活中对“量”的感知抽象出数的概念，这符合知识的逻辑结构和学生的认知顺序。教材从“半个”切入分数教学。“半个”是二分之一个，表示具体数量；二分之一表示把一个整体平均分成两份，其中的一份与这个整体之间的关系。

（一）通过语言转换生活现象，激活数学思维

半个是一个的一半——量与率的转换。语言是思维的物质外壳。通过语言转换，促使学生从感性体验走向深层认知。依据情境图提供的信息，学生主动将每种食品均分给两位小朋友（每人2瓶矿泉水、1个苹果、半个蛋糕）。针对均分结果，教师提出问题：每人分得的矿泉水、苹果都能用具体的数量表示，半个蛋糕是什么意思？通过课件演示将一个蛋糕分成大小不等的两半，激发学生的认知冲突，明确半个是平均分得到的。然后演示均分过程，让学生指出“半个”在哪里、有几个“半个”。这一环节表面上是判断“半个”量的大小，实质上是渗透“半个”与“一个”之间的关系。接着引导学生看图思考：半个蛋糕就是这一个蛋糕的……有了前期铺垫，学生很快就得出“半个就是一个的一半”。看似是生活经验之间的转换，实际上是“二分之一个是一个的二分之一”从量到率的数学转换，激活了学生的数学思维。

（二）再创造兼容数学史，催生理性思维

寻求“二分之一”的本质特征时，教师借助蛋糕图，让学生体会“一个的一半”比“0”大且比“1”小，无法用整数表示，可以通过画图表征进行再创造，如将实物图或平面几何图形（线段图、长方形、正方形、圆形等）均分成两份后涂出一份来表示。接着引导学生对比发现，“平均分、分2份、取1份”是这些表征的共性，亦即二分之一的内涵。超越表征技能，揭示“具有这些特征的一半用二分之一表示”成为必然，再融入数学史介绍二分之一的由来，以此固化学生新生长出的数学思维。

二、经验→思维：超越具体提升思维品质

通过回顾反思、沟通联系、归纳总结、优化认知等思维分析活动，加工、改造数学活动经验，学生更容易理解和掌握数学本质，体会普遍的思维模式或方法策略。

（一）改造经验，构建知识思维双结构

数学学习不是数学活动经验的简单累积，需要教师设置适切的问题，引导学生自觉、主动地对自己获得的经验进行加工改造，从而实现知识与思维的双建构。

1.核心问题引领，回顾反思促理解。

分子“1”表示均分多份中的任意一份。任何类型的思维守则都在于掌握和恰当地运用一系列合适的提问，启发和引领学生的思维。受直觉思维的影响，学生常会错误地认为“分子1”表示“1个蛋糕”。因此，借助多种表征的共性介绍“这样的一半用二分之一表示”后，教师及时组织学生观察思考：现在知道“这样的一半”为什么用二分之一表示了吗？依据直观表征，学生明晰了“二分”就是平均分成两份，“之一”就是两份中的任意一份。问题引领彰显个体思维，促使学生将感性经验提炼成理性认识，深度构建出了分子的意义（表示选取的份数）。

对二分之一的理解从具体向一般性过渡。核心问题能驱动学生遵循知识逻辑结构加工数学活动经验，使得新知与已有的知识、经验建立同化或顺应关系，提升学生的思维品质。针对“蛋糕的一半就是蛋糕的二分之一”，教师要求学生思考：蛋糕的二分之一是什么意思？在回顾反思中归纳总结：把一个蛋糕平均分成两份，每份都是它的二分之一。引发学生再思考：这句话中的关键词是什么？“每份”“它的”指的是什么？问题链推动学生深度思考，让学生感受“平均分”在分数中的重要性，体会分子“1”与单位“1”（1个蛋糕）之间的联系与区别。教师继续引发学生思考：还能找到其他的二分之一吗？能说说什么是二分之一吗？推动学生对二分之一的理解从具体形象思维向一般性思维过渡，为其认识几分之一做好经验迁移准备。

2.结构化联系，储备后续学习经验。

统一量与率的关系，为后续学习做好孕伏。教师要注意从整体上分析思考相关联的各个教学内容，把握它们各自的逻辑关系及其相互间的内在联系，精致化处理每个教学细节，相机为学生播下思维的“种子”。“分数的初步认识”涵盖了量与率的关系，既为高段学习“分数的意义”积累感性经验，也对“分数与除法的关系”的教学影响深远。当学生理解了二分之一，能厘清分子“1”和单位“1”（1个物体/图形）的区别后，教师可以借助具体情境组织学生思考：用二分之一表示（这样的）“一半”，那“半个”该怎样表示？通过交流明确：“半个”就是二分之一个；二分之一个是一个的二分之一。量与率的统一，为学生建构整体知识结构奠定了基础，使得具体思维方法更具有普适性。

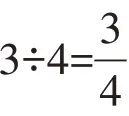
（二）超越技能方法，生长高阶思维

要将具体认知上升到一般性的数学思维，教师应注意引发学生更为深刻的思考，促进他们超越表象认识数学本质，提升思维品质。

1.操作体验，归纳总结见真知。

在数学操作中，教师应注意引导学生加深体验，在体验中归纳思考，寻求正确的逻辑结构，力求建构准确的认知，促进思维发展。学生通常会用对边折或对角折的方法找到正方形纸的二分之一。教师可以引导学生比较两种不同的折法，并思考：每份形状不同，为何都用二分之一表示？进而发现“折法不同，每份形状不同，却都表示均分的两份中的一份”，充分凸显平均分在分数中的价值。

2.透视表象，优化认知促生成。

在动手操作及直观体验的基础上，引导学生对初步形成的技能、方法进行对比优化，突破浅层认知，触及数学本质，有助于促进学生的思维向高阶发展。出现两种折法后，教师可以启发学生探究其他折法，在他们发现用不同的折法也可以得到两个同样大的梯形后，引导他们说明其中是否也有二分之一。接着，教师用课件演示几种不规则的平均分，鼓励学生找出并解释二分之一的意义。有了采用非对折方法寻找二分之一的体验，学生才能突破表象的桎梏，领悟“平均分”的深层含义：任一形状，只要平均分成两份，每一份都能用二分之一表示。

三、指导→自主：超越引领学会学习

数学教育不仅要培养和训练学生的思维能力，还要促进学生逐步从教师指导下的学习转变为自觉学会学习，并能通过数学学习学会思维。因此，教师要注意处理好教学中“引”与“放”的关系。

（一）引发生活经验先行猜测

生活经验告诉我们：平均分的份数越多，每一份就越小。教师教学时应注意鼓励学生根据已有经验先行“动脑”判断，感受数学知识的逻辑结构后再动手操作验证。比较几分之一的大小，可以先让学生说说“在这个蛋糕上还可以找到几分之一，分别表示什么意义”，并根据学生的回答引发其思考：分数是个数，就会有大小之分。那么，蛋糕的几分之一最大？学生根据分蛋糕的经验得出“平均分的份数越多，每一份就越小”“二分之一最大”。接着，教师引导学生凭借经验完成对几分之一大小的预判。

（二）放手让学生自主思考研究

“同样大的圆片”是比较分数大小的前提。以生活体验促进学生展开数学思维，建立完备的知识思维双结构，需启发学生“数学地思考”。教学时，教师可以引导学生先在各自同样大的圆片上创造不同的几分之一，验证“平均分的份数越多，每一份就越小”，并用数学事实证明几分之一中二分之一最大，加深学生对分数的理解。然后，引导学生通过交流组内各不相同的圆片，发现：大小不等的圆片上有相同的分数，同一个分数在不同的圆片上大小不等。随后，启发学生深度思考：分数的大小比较是否需要条件？进而得出“同样大小的物体或图形”是“平均分的份数越多，每一份就越小”的前提，也是本节课比较几分之一大小的默认前提。

综上可知，帮助学生遵循知识的逻辑结构建立优质的认知结构，需要从整体上深度研读教材，依据学生实际重构教学内容，设置核心问题启发引领，用联系的观点缔结相关知识的内部逻辑，才能让学生超越具体的知识技能深入到思维层面，学会数学地思维，生成一般性的思维策略，真正成为学习的主人。