基于涨落耗散理论的能量本征态规范研究

郭 凯

（华能武汉发电有限责任公司，湖北 武汉 430415）

0 引言

热涨落是物理学中的基础现象之一。基于统计物理理论，涨落耗散理论（fluctuation dissipation theorem，FDT）主要描述分子的随机运动导致系统的能量损失，在远离热力学平衡条件（熵最大值）下，系统的熵会在某一定时间中增加或减少的相对概率［1］。尽管分子运动的动能很小，但是，在超精密测量领域中，例如，地基激光引力波探测器，分子运动导致的热涨落占据主要的噪声贡献［2-4］。热力学第二定律预测了一个独立系统的熵应该趋向增加，直到其达到平衡为止。但是，在统计力学被发现后，物理学家才发现第二定律只是统计上的一种行为，因此，应该总有一定的概率使得独立系统的熵会自发性地衰减；而涨落定理准确地量化了此概率［5］。这个定理与物理学中的许多现象、概念和定理有着密切的联系，而且广泛应用于布朗运动、磁介质磁化、电介质极化、回路中的热涨落导致的电噪声、等离子体、固体中的光散射以及各种输运过程等问题［6］。

涨落耗散是热平衡态的理论形式之一，它提供物体的反应（即耗散，dissipation）与关联（即涨落，fluctuation）的统一关系［7-8］。独立的量子多体系统是否接近于热平衡态是一个值得深入研究的问题，例如，在量子热化过程中，关于超冷原子的探测与应用的理论研究和实验研究都引起人们的广泛兴趣。一个独立的量子系统进入一个稳态后的缓和态已经在大范围系统与初态之间得到验证。热化过程则需要稳定态与平衡微正则态之间存在区别。随着平衡动力学被详细的量化，热平衡系统的动力学反应函数和相关函数不是相互独立的关系，而是彼此之间紧紧联系。涨落耗散理论已经被用于区别平衡与非平衡动力学［9］，以及用于测量微观量子系统的温度［10-11］。

本 征 热 化 假 说（eigenstate thermalization hypothesis，ETH）弥补了稳态与Gibbs 态之间的理论空白。ETH表示局域可观测量的矩阵元素在哈密顿本征态中的假说条件。在这种条件下，可观测量的期望值与微正则态系统平衡均值一致。在不可积分系统中，ETH 已经被广泛验证，且可观测量的矩阵元素显示了ETH的统计性质。在量子湮灭与热动力作用之后的热化过程也能在ETH 条件下得到很好的解释。在一个独立的量子系统中，大量的工作已经或正在研究量子热力学与涨落和耗散之间的关系。文献［12］和文献［13］已经研究了非热可积量子系统的弛豫动力学性质。基于Lieb-Robinson 边界条件［14］，文献［15］提出了一种静态与动态关联的争议关系。文献［16］研究了一种独立量子系统的FDT，它涉及到可观测量的期望值的关系，这相当于全量子力学FDT 的经典极限［17-18］。文献［19］已经证明单个可观测量的FDT符合本征热化假说，两个不同可观测量的FDT 则需要假定随机变量的行为，本征热化假说也需要进一步得到验证。

在Gibbs 态中，涨落耗散理论是热平衡系统的重要特征之一。但是，现在的问题是能否在一个能量本征态的独立量子系统中验证涨落耗散理论的合理性与正确性？在本征热化假说条件下，可通过能量本征态或对角矩阵的双时相关函数计算得到规范的表达式。在无限大系统条件下，这种规范表达式既是FDT 的充分条件，也是FDT 的必要条件。此外，在有限大系统中，这种规范表达式也能获得有限的相关关系。即，无论是有限大系统，还是无限大系统情况下，能量本征态的规范表达式可以通过涨落耗散理论进行合理的解释［20］。

1 能量本征态的规范研究

1905年，爱因斯坦发表论文讨论了一定温度条件下，悬浮于液体介质中微小粒子的运动规律，即布朗运动［21］。因此，涨落耗散的研究可以追溯爱因斯坦。若液体介质中微小粒子的浓度n是不均匀的，那么液体介质会存在梯度为p的渗透压力。由于渗透压力的作用，微小粒子就从浓度高的地方流向浓度低的地方，若把布朗运动粒子作为理想气体，其压力梯度p与粒子浓度n的关系可表示为

事实上，做布朗运动的粒子由于热运动作用，存在两种流动形式，分别定义为扩散流和漂移流。扩散流是由粒子浓度不均匀导致，漂移流是受力的作用产生。因此，可把粒子平衡式（2）当作扩散流和漂移流的平衡，即有关系式

式（4）中，μ表示粒子的迁移率；μG表示粒子的漂移速度，它主要是由于重力G、粒子与介质的摩擦决定；D表示粒子的扩散系数。通过详细比较式（3）和式（4）之间的差异，可以得到

在统计物理学中，在满足给定宏观条件系统的所有稳定状态下，宏观物理量的定义为相应微观物理量的平均值，其数学表达式为

式（6）中，Bs表示微观物理量；ρ表示微观物理量的密度分布；S表示分布区域。采用偏差平方的平均值表示B对Bˉ的涨落，得到涨落耗散的准热力学理论关系式

因此，式（5）是爱因斯坦关于涨落耗散理论研究的雏形。其核心思想是原子的独立性，即原子的数目、原子的大小都具有有限性，这都可能在涨落耗散现象式（7）中显现出来，这种涨落耗散理论的概念正是统计物理学中表现粒子的规律性及其核心思想。

2 涨落耗散理论应用探讨

熵增原理可以简单地描述为孤立系统经绝缘过程由一状态达到另一状态，熵值只可能增大，不可能减少。这个定律最先在1864 年首先由克劳修斯提出。在统计力学被发现后，物理学了解到热力学第二定律只是一个统计规律。波尔兹曼用大数定律在理论上证明了熵增原理［22］。

但是，学者发现应该有一些概率会使得独立系统的熵自发性地减少。为了证明该现象，波尔兹曼从而提出了涨落理论。涨落定律准确地量化了那些使熵自发性地减少的概率。其中，在讨论宏观系统时，涨落力通常可以忽略；而在讨论微小系统时，熵增定律往往不适用［23］。

此外，涨落是种理论，也是一个物理现象，最常见的涨落现象是布朗运动［24］。布朗用显微镜观察到一些比分子大数百亿倍的物体，如花粉。花粉在永不停息地作不规则运动，这种运动被称为布朗运动。布朗运动是由涨落引起的，花粉会受到周围气体或液体分子不停的撞击。如果各方向撞击机会均等，在合力为零的情况下，花粉是不会动的［25］。但实际上，由于涨落能的影响，花粉周围的区域内气体或液体分子的分布是不均匀的。从而使得撞击产生的合力并不为零，而是一种大小和方向随机变化的涨落力，这种力推动花粉不停移动。

一些精密测量仪器的微小部件也会发生布朗运动，这影响了测量精度，所以国内外学者对此开展了广泛研究［26］。以悬镜式电流计为例，在没有电流或电流没有变化的情况下，悬挂在石英丝上的镜子，会保持不停摆动，从而使得测量数据产生明显误差［27］。以往在研究这个问题时，考虑的是如何减少涨落力的负作用。而考虑涨落力的利用，可使该问题产生正面意义，并研究能量在这一过程中的利用。如当小镜子在涨落力作用下转动一定角度时，石英丝就拥有弹性势能。石英丝这种压电晶体被扭转还能产生电能等［28］。这些能量的数值不大，但从本质上说它是可以传递和转化的自由能。负熵和自由能本来就是密不可分的，涨落产生了负熵因而产生了自由能。

海洋深处有一种靠波力发电机提供能量的航标灯［29］。图1 所示是一种简单的波力发电机的结构原理，图中A是装置外的密封浮箱；B是用弹簧与水箱联在一起的重物；C是一个可双向转动的发电机，定子固定在浮箱上，转子的齿轮和重物相配合。对于波力能发电机而言，当海潮冲击浮箱时，将所含的动能传递给浮箱，并使浮箱产生位移。但箱内的重物并没受到直接冲击，且由于弹簧的缓冲作用以及自身惯性影响，这浮箱与重物之间就产生了相对运动，并带动介于两者之间的发电机往复转动起来。因此，这台波力发电机能在有波浪的海里不断输出波动的电能。

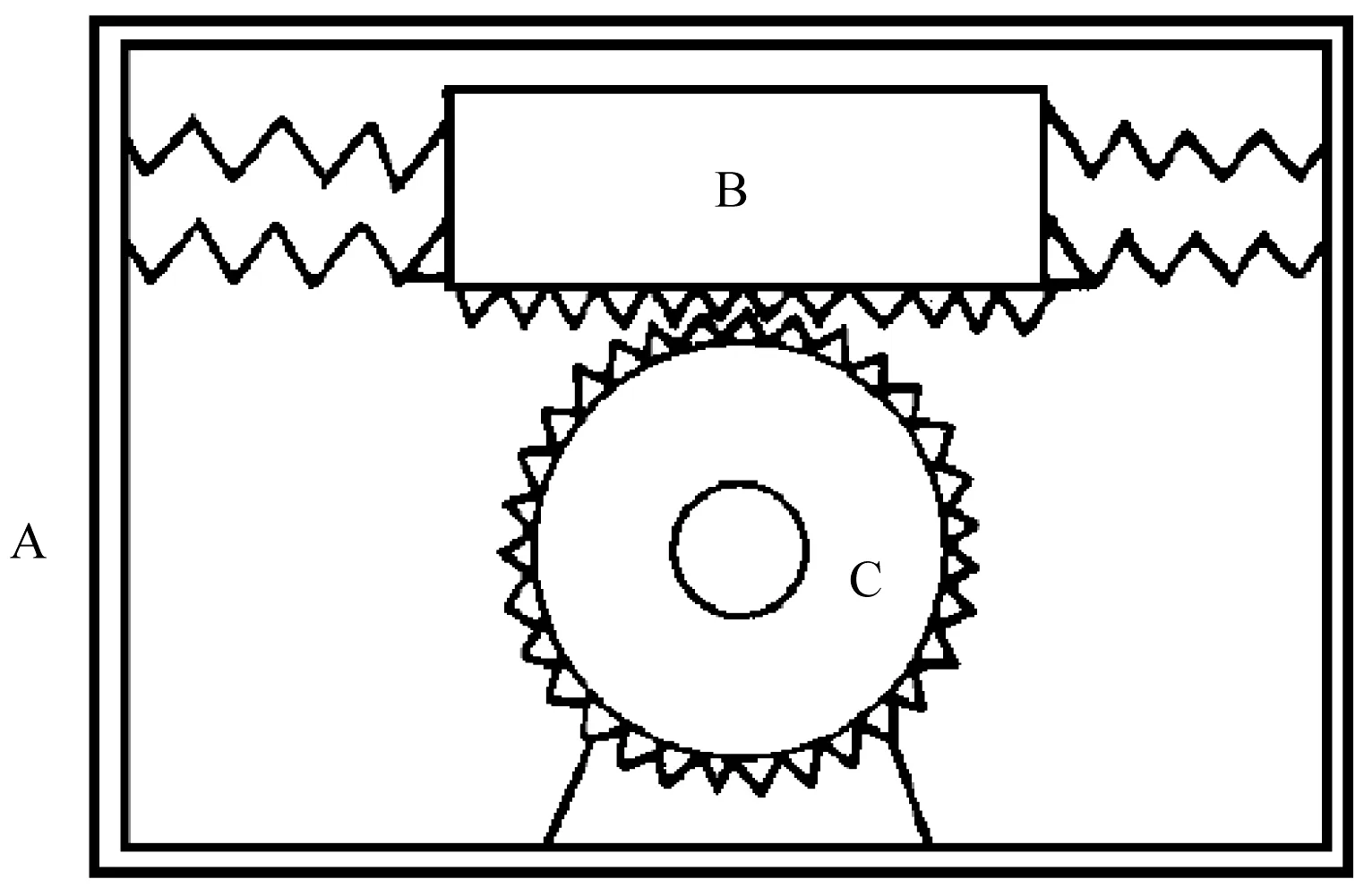
图1 波力发电机原理图Fig.1 Wave generator schematic diagram

帆船在航海时，遇到顺风就把帆张开乘风前进，遇到逆风就把帆扯下抛锚停下来，等到顺风重新来到。一根木头在海上漂浮的时候同样会遇到顺风和逆风，由于木头不能对不同风向的作用力进行选择，它只能在海上忽东忽西的梦游，很难向特定的目标进发。和随风飘流的木头不一样，帆船的行为是一种目的性的形为。学术界通常认为只有生物才能具有这种行为方式，要从物理学角度研究目的性行为，目前有进展但依然困难重重。

有种滑锁装置，它由一个弹簧闸和一个带齿的圆柱组成，前者叫滑车，后者叫滑道，滑道的一个斜面大于摩擦角，另一个小于摩擦角，如图2所示。

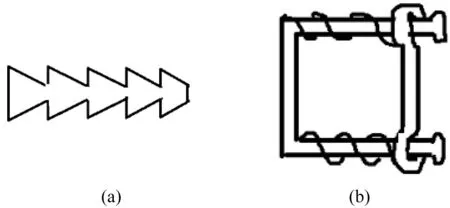
图2 滑锁装置简图Fig.2 Sliding lock device diagram

把滑车套在滑道上，可以推动它沿滑道前进。但不能把它往后推，反向推动滑车就卡在滑道上了。这样滑车只能沿滑道前进，不能后退。如果滑车小到一定程度就变成了一个“有理有智”的花粉，涨落力只能使它沿滑道前进，而不能使它后退和偏离滑道。这时在涨落力的作用下它的运动方式不是无规则的布朗运动，而是有规则的定向移动［30］。

滑车可以沿环状滑道永远地单向转动，也可以沿滑道爬升，如图3。滑车爬升过程中涨落产生的负熵和自由能并不是重新消失了，而是以重力势能的形式积累起来。本文只讨论了控制一个滑车爬升的工作原理，但用同样方法能使亿万个滑车进行同样的工作，如并排修建多滑道，或者在每个滑道上串入多滑车，那么就能把大量涨落能转换成重力势能，使问题进入宏观层次［31］。

图3 滑车示意图Fig.3 Schematic diagram of pulley

3 结语

作为近平衡态统计物理最重要的理论之一，涨落耗散理论深刻揭示了平衡系统同时存在涨落、耗散这两种根本现象之间的关联，且在宏观上通过平衡性质表现非平衡性质。在近平衡态热力学统计物理中，涨落耗散理论与输运系数对称理论、最小熵理论之间都存在密切关系，且输运系数对称理论可根据涨落耗散定理与微观可逆性导出，结合理论，对可能的应用方向进行了探讨。