G-布朗运动环境下欧式期权价格数值模拟

陈毛毛,薛红,王琪

（西安工程大学理学院,陕西西安710048）

期权定价一直是金融数学的核心问题之一,最早可以追溯到1973 年,Black 和Scholes 发表了一篇题为“期权定价与公司债务”的论文,同时提出了著名的Black-Scholes 期权定价模型[1],得到了Black-Scholes 期权定价公式.但是Black-Scholes 公式中假设波动率为常数,这与实际金融市场并不相符,1985 年Rubinstein[2]首次发现实指和虚值期权的隐含波动率比较高,两平期权的隐含波动率比较低,并将此现象称为波动率微笑.为了解决这一问题,学者们提出了一系列随机波动率模型,假设波动率是随机过程,其中Scott[3]假定波动率服从指数过程,Hull 等[4]假定波动率服从平方根过程,Shanno[5]提出了不确定波动率模型.另一种对Black-Scholes 模型的修正是以Cox 等[6]、Geske[7]、Rubinstein[8]和Bensoussan 等[9]为代表,利用具有价格依赖型波动率的扩散过程来描述股票价格,认为波动率是股票价格和时间的函数.彭实戈[10]在2006 年引入了次线性期望空间,在G-框架下构造了相应的G-布朗运动.且得到了一系列重要结果,参见[11-14].文献[15]讨论了G-正态分布和G-布朗运动的数值模拟,文献[16]讨论了G-布朗运动二次变差的模拟,徐静等[17]给出了G-框架下的欧式期权定价公式.但是并没有学者利用G-布朗运动进行期权价格的模拟计算,上证50ETF 期权在2015 年2 月上市,研究其对于中国发展金融衍生品市场具有重要借鉴意义.本文在G-布朗运动环境下建立金融市场模型,假设股票价格服从由G-布朗运动驱动的随机微分方程,利用蒙特卡洛方法以及保险精算方法数值模拟计算期权价格并用50ETF 进行实证分析.

1 预备知识

定义1（G-正态分布[12]）在次线性期望空间中,如果一个随机变量满足

定义2（G-布朗运动[12]）次线性期望空间上的实值随机过程称为G-布朗运动,如果对每一个,有,且满足两条性质：

（1）B0=0；

（2）对每一个t,s＞0,增量Bt+s-Bt服从,并且对每一个,增量

定义3（二次变差过程[13]）G-布朗运动的二次变差过程定义为

引理1假设U 服从上的均匀分布,F 是一个严格递增的连续分布函数,那么F-1（U）服从分布F[18].

算法1模拟G-布朗运动及其二次变差过程的步骤如下：

Step1：在方程

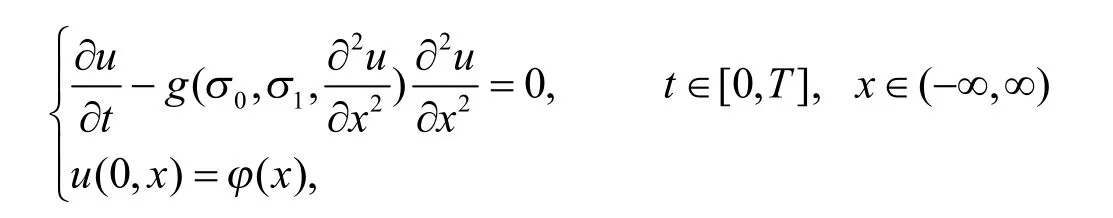
Step2：生成n 个在区间[0,1]上服从均匀分布的随机数

Step4：由于G-布朗运动的增量 Bti-Bti-1服从分布,且对每一个 i = 1,2,…,n,均独立于把Step3 得到的xi, i = 1,2,… ,n 逐项累加就得到一条G-布朗运动的轨道；

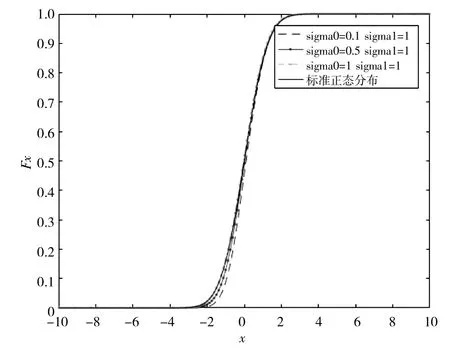
图1 G-正态分布的分布函数 Fig.1 G-normal distribution function

图2 G-正态分布的密度函数Fig.2 G-normal density function

G-布朗运动及其二次变差的轨道见图3 和图4.

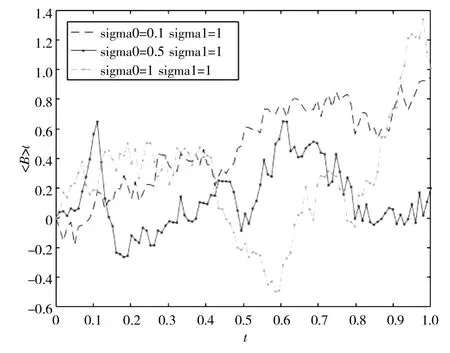
图3 G-布朗运动的样本轨道 Fig.3 Sample path of G-Brownian motion

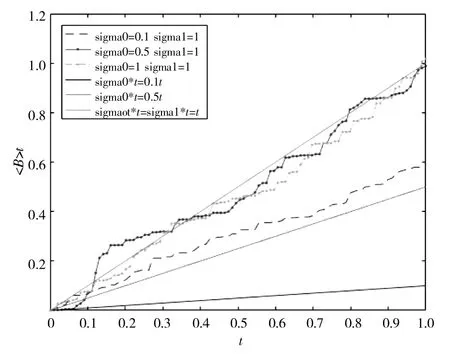
图4 G-布朗运动二次变差的样本轨道Fig.4 Sample path of ＜B＞t

2 基于G-布朗运动的欧式期权数值模拟

2.1 股价基本模型

假设股价满足随机微分方程

式（2）中：St代表t 时刻股价,μ 为期望收益率,Bt为G-布朗运动,

式（3）中：＜B＞t为G-布朗运动的二次变差过程.

2.2 参数估计与数值模拟

随机微分方程（1）的离散形式为

故有

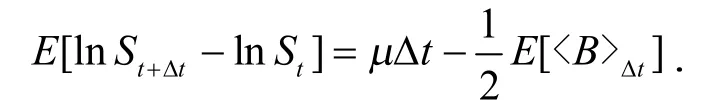
即

计算每个窗口的方差,取其中最大值为总窗口中的方差上界,即,取其中最小值为总窗口中的方差下界,即.在μ 已经被确定的情况下可以获得关于下方差和上方差的最优渐进无偏估计

式（6）、式（7）中：风险资产按其期望回报率贴现,期望收益率无风险资产按无风险利率r 贴现.

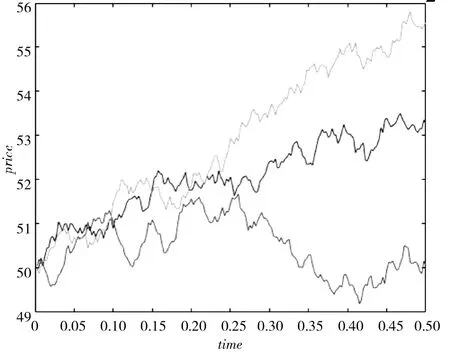
图5 基于布朗运动的股价3 条样本轨道 Fig.5 Three sample paths of stock prices based on Brownian motion

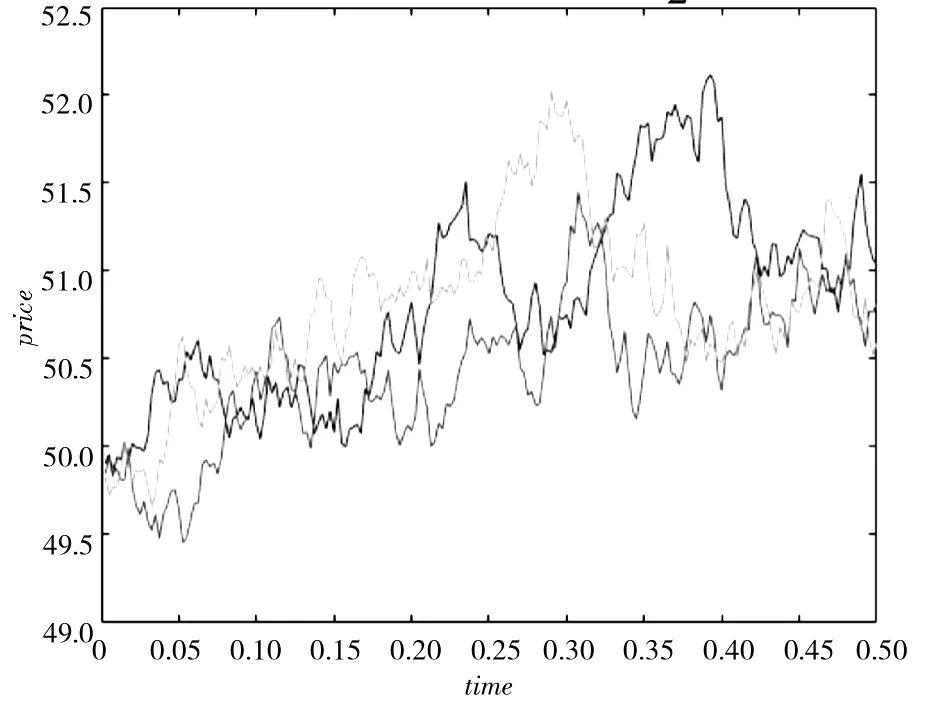
图6 基于G-布朗运动的股价3 条样本轨道Fig.6 Three sample paths of stock price basedon G-Brownian motion

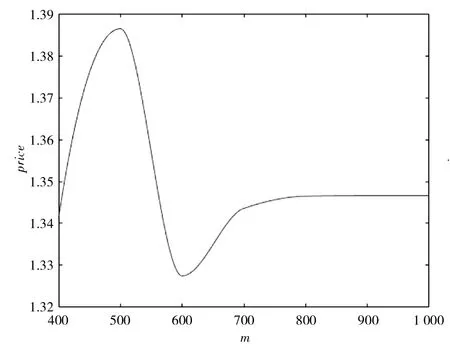
图7 不同模拟次数下的欧式看涨期权价 Fig.7 European call option price with different simulation times

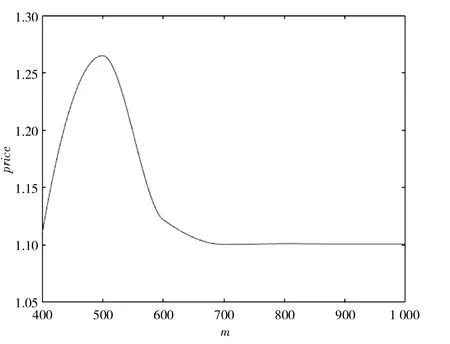
图8 不同模拟次数下的欧式看涨期权价格Fig.8 European put option price with different simulation times

3 实证分析

选取50ETF 期权（标的物代码为510050）来进行实证分析.选择2018 年10 月23 日中到期日为11月28 日的全部合约,基本信息见表1.已知2018 年10 月23 日50ETF 的收盘价格为2.511 元,即S0=2.511,因此模拟接下来26 个交易日的股票价格走势,无风险利率选取央行2018 年定期存款3 个月的利率,为1.1%,故r=0.011.所用到的数据来源于交易所行情数据借接口.

表1 上证50ETF 的基本信息Tab.1 Basic information of SSE 50ETF

3.1 参数估计

对G-布朗运动的参数进行估计时选取滑动窗口法, 根据2018 年1 月2 日至2018 年10 月23 日50ETF 数据,将对数收益率序列看作总窗口M,子窗口长度N 设为24,共有171 个窗口,计算出上方差和下方差分别为

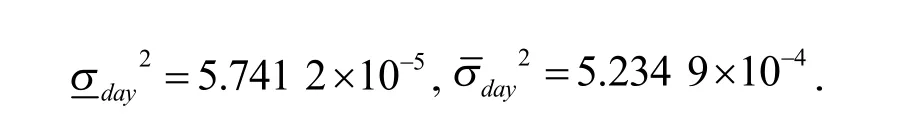
同样,对数收益率序列的均值

即

在布朗运动环境下进行参数估计时计算得到对数收益率序列的均值μ 和波动率

故

即

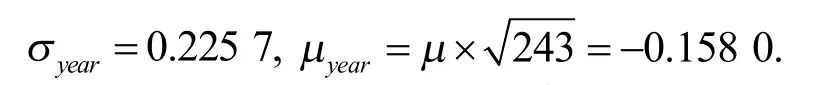
3.2 结果分析

表2 为分别利用Black-Scholes 公式所计算的看涨、看跌期权价格与布朗运动环境下和G-布朗运动环境下的模拟计算的看涨、看跌期权价格对比分析.

利用表2 数据,可得3 种方法计算结果与实际价格的均方误差：

（1）Black-Scholes 公式下均方误差

（2）布朗运动环境下均方误差

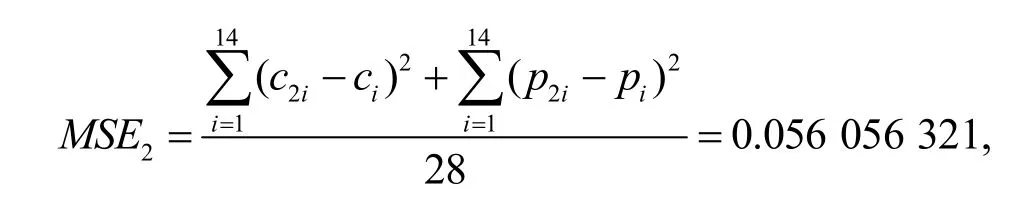
（3）G-布朗运动环境下均方误差

通过上面的分析可以看出,MSE3＜MSE2＜MSE1,G-布朗运动下模拟的期权价格较Black-Scholes 公式以及布朗运动环境下模拟的期权价格而言,能更好地刻画市场运动,并得到较精确的市场定价,再次说明了G-布朗运动比布朗运动更适合描述复杂的金融市场.

4 小结

本文通过假设股票价格随机微分方程由G-布朗运动所驱动,模拟股票价格轨道,利用保险精算方法模拟计算期权价格,同时用50ETF 真实数据进行实证分析,利用一系列模型进行对比,得出G-布朗运动环境下的期权定价模型比布朗运动环境下的期权定价模型偏差小, 故G-布朗运动能得到较合理的市场期权定价的结果.总体而言,G-布朗运动环境下的数值方法比布朗运动环境下的数值方法更具有优越性.