关于数列极限求法的探讨*
2021-11-15 08:56刘喜富王艳辉
读与写 2021年29期
刘喜富 王艳辉
(重庆师范大学数学科学学院 重庆 401331)

1.利用等价替换求极限



2.利用两个重要极限求极限

因此可得

3.利用夹逼定理求极限
无法直接求数列极限时,可以将数列适当的缩小和放大,使得缩小、放大后的数列易于求出其极限,且具有相同的极限值,则原数列极限存在,且等于二者的共同值。




4.利用单调有界定理求极限
我们知道单调有界数列必有极限[1]。在运用此定理时,通常先根据数列的特点,证明该数列是单调有界,然后假设其极限为a,然后通过解方程求出的值,且要注意根的取舍问题。
例4:证明下列数列极限存在,并求其极限值:设





5.利用定积分定义求极限
当遇到极限形式是和或者积的形式时,先判定其是否可以化作某一个函数在某一区间上的积分和,如果可以,则原极限就可以转化为计算一个定积分。
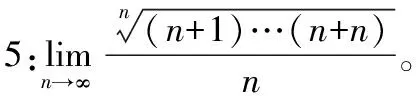
解:先化解极限式
根据定积分定义式,有

6.利用级数求极限
在求数列极限时,有些数列可以通过判断级数的收敛性,进而来求通项的极限。

4.结束语
数列极限的求解方法有很多,通过对一些方法和技巧的整理,在做题时,我们可以根据题目特点,选择合适的方法进行求解。当然,有时候一道题需要运用多种方法进行求解,除了一些基本的方法,特殊方法也是需要我们去考虑和筛选的,有时可能会达到意想不到的效果。因此,这就需要我们对各种方法的熟练和透彻的了解。
猜你喜欢
科技风(2022年26期)2022-10-10
中学生数理化(高中版.高二数学)(2022年3期)2022-04-26
中学生数理化(高中版.高考数学)(2021年11期)2021-11-24
中学生数理化(高中版.高考数学)(2021年6期)2021-07-28
语数外学习·高中版上旬(2020年10期)2020-09-10
中学生数理化(高中版.高考数学)(2019年5期)2019-11-28
中学生数理化(高中版.高考理化)(2019年6期)2019-11-26
知识文库(2019年4期)2019-10-20
华东师范大学学报(自然科学版)(2019年3期)2019-06-24
学苑创造·A版(2018年7期)2018-08-07

