基于EWT−MCKD的机车轮对轴承故障诊断
张龙,闫乐玮,熊国良,胡俊锋
(1.华东交通大学 机电与车辆工程学院,江西 南昌 330013;2.中国铁路南昌局集团有限公司 科学技术研究所,江西 南昌 330013)
轮对轴承作为高速列车走行部的“关节”,长期处在高速运行的状态下,不仅承受机车车体自重的垂向力,在列车转向时还承受着轮轨间的径向力。在多种外力的联合作用下,轮对轴承极易产生故障,而机车在高速运行的状态下一旦产生故障,将造成一系列的、难以预料的后果。因此,轮对轴承的故障诊断一直是研究的热门之一。机车轮对轴承的故障诊断方法主要有直接观察法、温度检测法、油液光谱分析法和振动噪声频谱分析法等。其中,振动噪声频谱分析法适用性高、效果好,测试信号处理简单直观,使用最广泛。在振动噪声频谱分析法中,信号处理是非常重要的一个环节,其目的是去除得到的信号中的噪声,将信号转变成容易识别和处理的形式,以便于后续的研究处理。经验模态分解自HUANG等[1]于1998年提出后,一直在信号处理方面发挥着重要的作用,其没有任何函数公式,而是依据原信号的时间尺度对信号进行分解,理论上可以应用在任何类型的信号上,因此在处理非线性非平稳信号上具有明显的优势。LIU等[2−3]用经验模态分解方法研究分析了轴承和齿轮箱,都得到了比较好的结果。但不可否认的是,EMD没有一个准确的函数关系式,缺乏理论基础,且端点效应和模态混叠始终是待处理的难题。为了抑制模态混叠效应,WU等[4]在2009年首次提出集合经验模态分解,EEMD方法利用了高斯白噪声在频率范围内均匀分布的统计特性,并且噪声辅助信号不仅具有均匀的尺度去分解,而且还平滑了脉冲干扰等异常状况,可以良好解决模态混叠的问题。但是EEMD方法中仍然存在大量不敏感的IMF分量,还需要经过筛选和去除[5],这无疑增大了工作量。基于此问题,GILLES[6]于2013年提出了经验小波变换,该方法不仅具有严谨的函数公式,还去除了繁多的IMF分量,而且没有出现模态混叠的问题,在旋转机械的故障诊断[7−8]及寿命预期[9]等方面都有良好表现。然而在实际工作环境中,总是面临着强噪声的严重干扰,虽然EWT仍然还可以很好的将Fourier频谱分段并得到模态分量,但是得到的模态分量中混杂着与故障冲击相似的噪声成分,导致其包络谱分析的结果往往并不理想[10]。因此在对EWT的改进方案上,需要对模态分量进行降噪处理。峭度是降噪方法中常用的一种指标,对冲击信号特别敏感,特别适用在轴承表面早期损伤的检测,但在强噪声环境下易受到干扰,从而无法表征出冲击成分[11]。相关峭度在峭度的基础上增加了解卷积周期T和移位数M的概念。当解卷积周期T与轴承故障周期相同的话,相关峭度值会很大,说明信号中的故障冲击成分占比大。移位数M的增加弥补了峭度在处理周期性冲击信号上的不足,因此特别适合应用在轴承的故障诊断上[12]。重载高速、高寒高温的恶劣工作环境使得机车轮对轴承频发故障,本文提出的EWT-MCKD方法将2种方法有机地结合到一起,前者可以将掩藏在强噪声下的机车轮对轴承振动信号有效地分离出来,后者则可以很好地表达出故障信号的周期性,仿真信号和实验信号均验证了该方法的可行性。
1 理论基础
1.1 经验小波变换
经验小波变换是由GILLES[6]在2013年提出的一种信号处理的技术。EWT的优点是可以设计适当的小波滤波器来提取信号的不同模态。每个模态对应信号中包含的一个单声道AM-FM分量,且有紧凑的傅里叶频谱支撑[13]。因此,从信号中提取一组模态,相当于用一组带通滤波器来分离信号中不同的AM-FM分量,并将每个AM-FM分量放入相应的频段中[14]。
首先确定分割区间,假设一段信号在傅里叶域[0,π]中被分为N段,每段用Λn=[ωn-1,ωn]表示,所以。可 以 用Littlewood-Paley和Meyer小波的构造方法来建立每段的经验小波,信号的经验尺度函数和经验小波分别为:
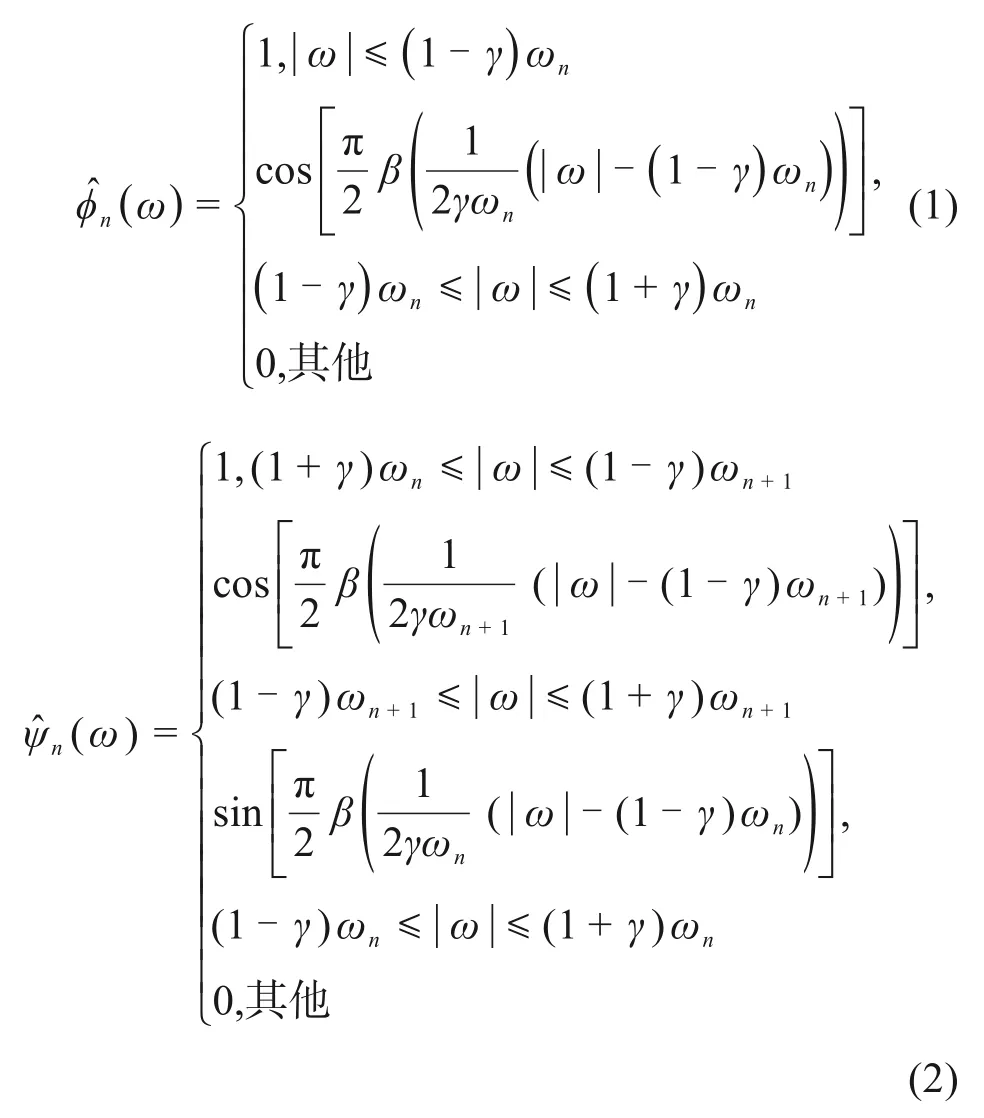
这里γ是决定小波框架的系数:

且当0≤x≤1时,β(x)+β(1-x)=1,满足条件的β(x)很多,最常用的为:

EWT的信号分解过程与小波变换相似,EWT的近似系数为信号和尺度函数的内积:

EWT的细节系数为信号与经验小波的内积:

EWT中的经验模态可以表示为:

重构信号的公式为:

1.2 最大相关峭度解卷积
最大相关峭度解卷积(MCKD)方法是MCDONALD等[15]在最小熵解卷积(MED)的基础上提出的一种新的解卷积技术,MED是一种曾广泛使用的去噪方法,它使用峭度作为去噪指标,但在处理周期性信号时,峭度会变得很小,不易被观察到,这使得MED在旋转机械的故障诊断中有很大的局限性[16]。MCKD将峭度改进为相关峭度(CK),其表达式为:

其中:M是移位的阶数;TS是迭代周期的对应采样点,可由式(12)得出:

其中:fS为采用频率;T为故障周期。
MCKD迭代的选择有限脉冲响应滤波器,使滤波后的CK值最大,结合反滤波器表达式(13),将MCKD的优化函数(14)对滤波系数f求导并使其为零,最终得到迭代表达式(15),得到最优滤波系数。
反滤波的一般表达式如式(13):

其中:xn是输入信号;yn是输出信号;f是滤波系数;L是滤波器长度;N是信号的采样数。
MCKD的优化函数表达式为:
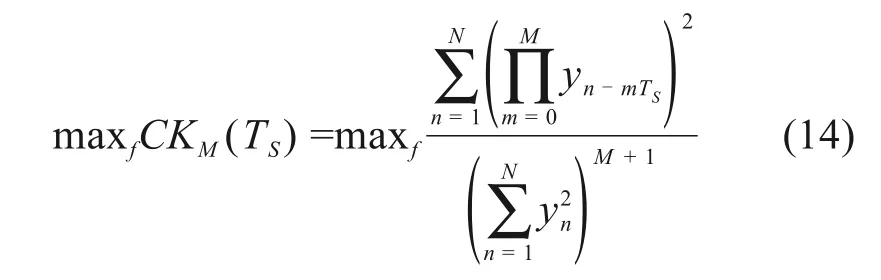
滤波器系数的最终迭代表达式为:

其中:X0XT0是原始信号x的toeplitz自相关矩阵,逆矩阵(X0XT0)-1是假设存在的,右上角的T表示转置。
式(15)中的Xr,αm,β分别如下:

1.3 EWT-MCKD流程
本文使用经验小波变换方法将振动信号分解为若干模态分量,以裕度因子为指标选出对故障最敏感的模态分量,再用最大相关峭度解卷积对其进行降噪处理分析,最后通过包络谱分析得出轮对轴承故障特征,其实现如图1所示。
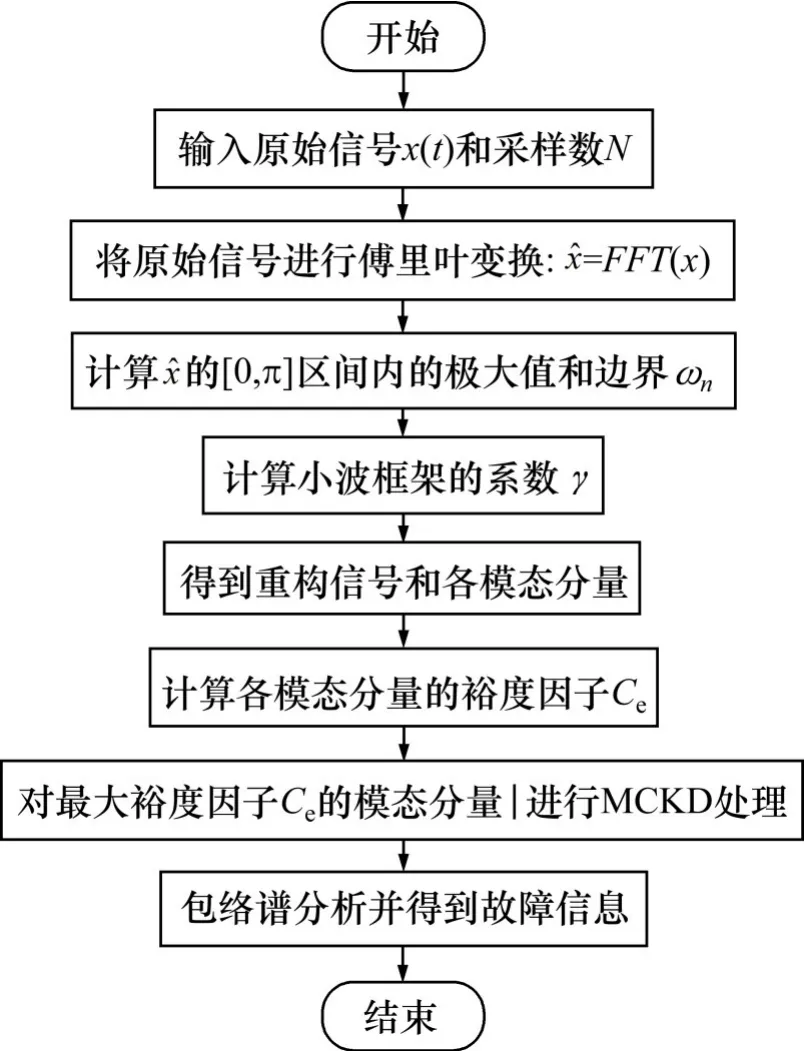
图1 EWT-MCKD流程图Fig.1 Flowchart of EWT-MCKD
基本步骤包括:
1)输入原始信号x(t)并进行傅里叶变换,得到傅里叶频谱x̂。
2)将x̂的[0,π]范围内分割为N段,计算范围内的极大值,个数记为M。则有如下2种情况:
M≥N:得到了足够的极大值,保留前N−1个极大值,M 3)计算EWT的近似系数和细节系数,并对信号进行重构,得到EWT的经验模态xn(t)。 4)计算经验模态xn(t)的裕度因子Ce。 5)对裕度因子最大的经验模态进行MCKD处理。 6)对结果进行包络谱分析,得到故障特征频率。 7)在仿真信号和实验信号上测试提出方法的有效性。 构建滚动轴承外圈故障仿真信号来验证提出方法的有效性,设系统的固有频率fn=3000Hz,采样频率fs=20 000 Hz,外圈故障特征频率BPFO=125 Hz,仿真信号表示为: 式中:ωn为固有振动角频率,幅值y0=5,阻尼系数ξ=0.1,采样点数为4 096。外圈故障原始仿真信号如图2所示,为使仿真信号能够更好地模拟真实的轴承早期故障信号,在仿真信号中添加了强烈的白噪声(SNR=−8),生成的仿真信号如图3所示,并对仿真信号进行了包络谱分析。由图3可以看出,原始仿真信号的冲击成分被强噪声掩盖,看不到明显的冲击成分,包络谱图中也得不到故障特征频率。 图2 外圈故障原始仿真信号Fig.2 Original simulation of the outer ring fault signal 图3 仿真信号时域图和包络谱图Fig.3 Time-domain and envelope spectrograms of simulated signals 普通的包络谱方法难以诊断仿真信号的故障,故引入本文提出的方法,将仿真信号进行EWT处理,在Fourier频谱中将仿真信号划分为3部分,如图4所示,再将各个频谱段分别重构,得到3个模态分量,如图5所示。 图4 仿真信号Fourier频谱划分Fig.4 Fourier spectral partitioning of simulated signals 图5 仿真信号EWT分解结果Fig.5 EWT decomposition results for simulated signals 计算各个模态分量的裕度因子Ce,其计算公式为: 其中:xpeak为峰值,xr为方根幅值。裕度因子对比其他因子(峰值因子、脉冲因子、波形因子、峭度因子等)在敏感性和稳定性方面均有更好的表现[17]。 图6给出了仿真信号3个模态分量的各项因子比较图,裕度因子是对故障的敏感程度是最强的,模态分量2最能体现仿真信号的脉冲成分。对模态分量2进行包络谱分析,如图7所示,得到的包络谱图得不到有用的信息,将模态分量2进一步做MCKD处理(参数设置为:L=300,T=163,M=5),结果如图8所示,可以清楚地看到,包络谱图中有3条突出的频率谱线,分别为f0(127 Hz),2f0(249 Hz),3f0(376 Hz),与理论外圈仿真故障频率基本相同。从分析结果可以判断,轴承外圈已经发生故障,本文提出的方法切实有效。 图6 3个模态分量的各项因子比较Fig.6 Comparison of factors for the three modal components 图7 模态分量2的包络谱图Fig.7 Envelope spectra of the second modal component 图8 模态分量3经MCKD处理后的包络谱图Fig.8 Envelope spectra of the third modal component after MCKD treatment 实验在南昌铁路局机车轮对轴承故障诊断实验室进行,试验平台为JL-501机车轴承动态诊断台,如图9所示。故障轴承为NSK NJ2232WB型可分离圆柱滚子轴承,外圈直径为290 mm,内圈直径为160 mm,节径为225 mm。图10(a)中故障轴承外圈滚道的故障大小约为30 mm×4 mm,图10(b)中故障轴承内圈滚道的故障大小约为56 mm×4 mm。其相应的内圈和外圈故障特征频率分别为BPFI=81.5 Hz,BPFO=60 Hz。试验采用3个CAYD-187T加速度传感器并安装在故障轴承外圈的竖直和平行方向上;使用national instruments数据采集仪采集故障轴承竖直和水平方向的振动信号,并在LabVIEW程序中处理信号数据,故障轴承转速为500 r/min,采样频率为20 kHz,采样时长为10 s。 图9 实验装置图Fig.9 Experimental setup 图10 轴承内外圈故障Fig.10 Bearing inner and outer ring failure 图11为内圈故障轴承竖直方向上加速度传感器采集到的一段(20 000个点)时域信号及其包络谱。由图11可以看出,时域波形图中存在较多的冲击波形,在包络谱图中存在一些幅值较大的谱线,但均不是内圈故障特征频率的谱线(60 Hz),因此无法判断是否发生外圈故障。 图11 内圈故障信号时域波形图和包络谱图Fig.11 Time domain waveforms and envelope spectra of the inner ring fault signal 对内圈故障信号的Fourier频谱进行划分,如图12所示,得到一系列模态分量,如图13所示。 图12 内圈故障信号Fourier频谱划分Fig.12 Fourier spectral delineation of fault signals in the inner circle 图13 内圈故障信号EWT分解结果Fig.13 EWT decomposition results for inner ring fault signals 根据计算得到的各模态分量的裕度指标Ce来选出包含最多故障信息的模态分量,各模态分量的裕度值如下表1所示。 由表1可知,模态分量2的裕度值最大,故选取模态分量2进行包络谱处理,得到如图14所示的包络谱图。 表1 内圈故障信号各模态分量的裕度值Table 1 Margins for each modal component of the inner ring fault signal 在图14的包络谱图中未能发现故障特征频率,故将其做MCKD处理(参数设置为:L=300,T=79,M=5),结果如图15所示,经MCKD处理后的包络谱图消除了绝大部分杂乱的无关谱线,包络谱图中转频fr(8.33 Hz)峰值突出,内圈故障特征频率及其倍频1~3fi(fi=81.2 Hz,2fi=163 Hz,3fi=244.8 Hz)清晰可见,并且被转频调制的边频带也清晰可见,和理论值相差无几,能够准确地诊断出轮对轴承内圈故障。 图14 模态分量2的包络谱图Fig.14 Envelope spectra of the second modal component 图15 模态分量2经MCKD处理后的包络谱图Fig.15 Envelope spectra of the second modal component after MCKD treatment 为了对比,采用EMD方法将上述内圈故障信号进行分解,计算得到的12个IMF的裕度因子,表2为前4个裕度因子较大的IMF,取其中裕度因子最大的IMF1进行MCKD处理。 表2 EMD处理后的各IMF的裕度值Table 2 Margin value of each IMF after EMD processing 图16(a)为IMF1的包络谱,图16(b)为IMF1经MCKD处理后的结果,图中没有提取出任何与内圈故障特征相关的信息。通过对比,更加验证了本文提出方法在频谱分割上有较好的效果,克服了传统EMD方法在频谱分割上的不足。 图16 内圈故障轴承经EMD方法处理后的结果Fig.16 Result of the inner ring failure bearing after EMD method 图17为1 s的轮对轴承外圈故障信号,时域信号有明显的周期冲击波形,而在包络谱图中频线杂乱,不能有效地提取出故障特征信息。故将故障信号经EWT处理,得到故障信号的Fourier频谱划分图,如图18,和得到的4个模态分量图,如图19。 图17 外圈故障信号时域波形图和包络谱图Fig.17 Time domain waveform and envelope spectrum of outer ring fault signal 图18 外圈故障信号Fourier频谱划分Fig.18 Fourier spectral partitioning of outer ring fault signals 图19 外圈故障信号EWT分解结果Fig.19 EWT decomposition results for outer ring fault signals 计算各模态分量的裕度值,结果如表3所示,模态分量2的裕度值最大,其包含的故障信息最多,故对模态分量2进行包络谱分析,结果如图20。 表3 外圈故障信号各模态分量的裕度值Table 3 Margins for each modal component of the outer ring fault signal 由图20的包络谱图可以看到,包络谱线依旧杂乱,得不到明确的故障特征频率,将模态分量2进行MCKD处理(参数设置为:L=40,T=83,M=5),并做其包络谱,得到结果如图21所示,可以看到得到的外圈故障特征频率61.65 Hz,2倍外圈故障特征频率122.7 Hz和3倍外圈故障特征频率184.3 Hz清晰且突出,与理论外圈故障特征频率相差不大,能够诊断轮对轴承外圈故障。 图20 模态分量2的包络谱图Fig.20 Envelope spectra of the second modal component 图21 模态分量2经MCKD处理后的包络谱图Fig.21 Envelope spectra of the second modal component after MCKD treatment 为了对比,采用EMD方法将本节外圈故障信号进行分解,计算得到的11个IMF的裕度因子,下表4为前4个裕度因子较大的IMF,取其中裕度因子最大的IMF1进行MCKD处理。 表4 EMD处理后的各IMF的裕度值Table 4 Margin value of each IMF after EMD processing 图22(a)为IMF1的包络谱,图22(b)为IMF1经MCKD处理后的结果,在图中得不到有用的外圈故障信息。综上,本文提出的方法优于传统的EMD方法。 图22 外圈故障轴承经EMD方法处理后的结果Fig.22 Result of outer ring failure bearing after EMD method 1)小波变换在信号的分解和重构上有很大的优势,其具有完备的理论基础,没有模态混叠效应的产生,有较强的鲁棒性。 2)最大相关峭度解卷积则有效地弥补了经验小波变换在强噪音环境下的不足。 3)衔接2种方法之间使用的裕度指标可以有效地选择出包含最多故障特征信息的模态分量,极大地减少了工作量。 本文通过分析仿真信号和实验信号,验证了EWT与MCKD相结合方法的有效性,在实际工程应用中有一定的使用价值,下一步考虑如何能更科学地划分傅里叶谱。2 仿真信号分析








3 实验信号分析
3.1 实验装置和数据采集


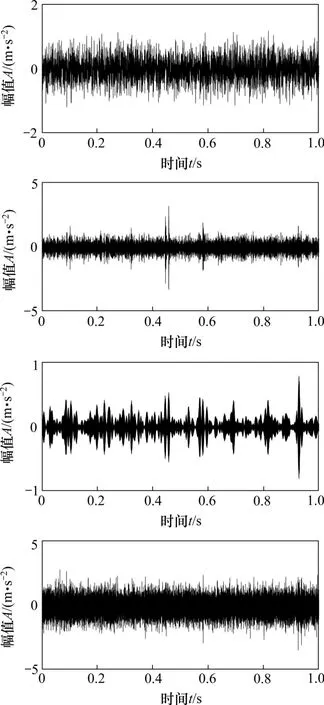
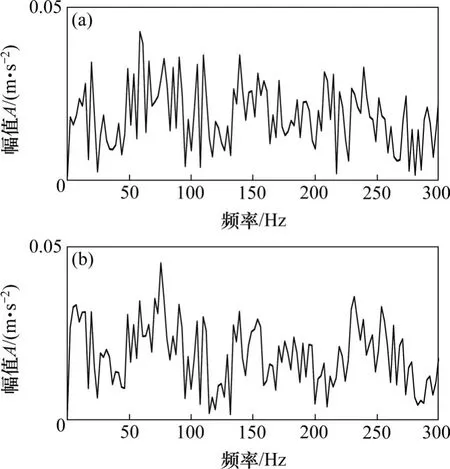
3.2 内圈故障试验信号分析






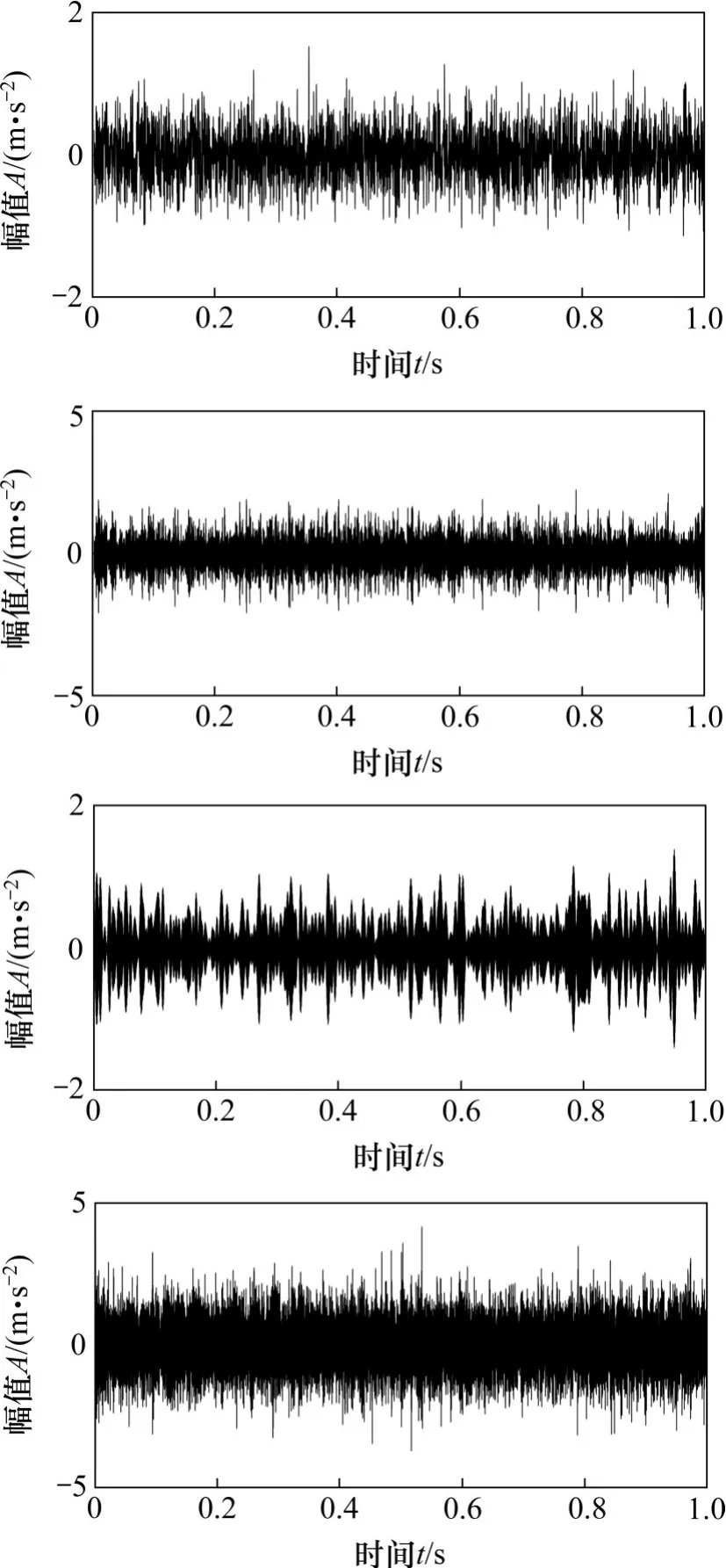
3.3 外圈故障试验信号分析







4 结论

