装配式建筑施工质量风险评估模型的构建与应用研究

陈蓉芳，姜安民,2，董彦辰,2，熊奇伟，陆银锐

(1.湖南城建职业技术学院，湖南 湘潭 411100；2.中南林业科技大学 土木工程学院，湖南 长沙 410004；3.湖南大学 土木工程学院，湖南 长沙 410082；4.中建八局苏南建设有限公司，江苏 苏州 215000)

部品部件预先在工厂完成加工，施工现场工人采用机械吊装方式进行装配，最终所形成的建筑即装配式建筑[1]。装配式建筑有着节能环保、缩短建设周期等诸多优点，大大提高了资源、能源的利用率，促进了建筑业的转型升级[2]。2017年起，我国开始全面推进装配式建筑的发展[3]，在国务院发布的《关于大力发展装配式建筑的指导意见》(国办发〔2016〕71号)文件中明确指出，力争用10 a左右的时间，使装配式建筑占新建建筑面积的比例达到30%[4]。在此背景下，学者们对装配式建筑施工质量问题展开相关研究。在装配式建筑施工过程中，施工质量的好坏直接影响了建筑结构的安全性、耐久性，也成为了影响装配式建筑在我国建筑业中推进进程快慢的关键因素。国外针对装配式建筑施工质量问题展开了大量研究，TAKENAGA等[5]对罗科岛市东院3号楼装配式建筑施工质量问题展开研究，建立了质量控制体系；LEE等[6]对装配式建筑施工质量风险评估问题进行了研究，考虑的因素较为全面，对风险评价及风险影响程度问题研究得较为详细。除此之外，STAUB等[7−8]也分别从模拟施工及质量评估框架搭建等角度对装配式建筑施工质量问题展开研究。在国内，针对装配式建筑施工质量问题的研究主要集中在定性分析与量化评估2个方面，其中风险量化评估是研究的重点。王志强等[9,2,10−11]分别采用云模型法、模糊综合评价法、博弈法及粗糙集法对装配式建筑施工质量风险进行量化研究，确定风险所处等级。本文主要是对风险进行量化评估研究，并结合实例验证了评估方法的可靠性。为克服以往量化研究中权重计算不准确的缺陷，本文引入了区间层次分析法(IAHP)，在确定指标相对重要程度时运用数值区间代替单点数值，很好地解决了指标间相对重要程度较为模糊的问题，使得权重结果更加可靠；通过构造隶属度函数，确定指标隶属度，该方法可以很快地对单一指标风险等级的隶属情况做出判断。基于区间层次分析法与模糊理论的装配式建筑施工质量风险评估方法操作相对简单，具有较强的适用性。

1 装配式建筑施工质量风险评估指标体系

影响装配式建筑施工质量的因素较多且复杂，从不同的角度及阶段进行分析，所建立的评估指标体系也存在一定差异，但总体的划分方式有矩可循，即按工作先后顺序进行划分。如洪文霞等[12]将风险划分为构件供应、施工准备、施工过程、竣工验收4大方面，在此基础上进行详细划分并构建风险评估指标体系；刘占坤等[13]则分为设计、生产、运输、安装4大类。本文同样遵循工作先后原则进行大类划分(划分及建立过程见图1)，参考文献[11,14−15]并听取专家建议，建立装配式建筑施工质量风险评估指标体系。本指标体系贯穿从设计到施工完成的主要质量控制点(规范控制点及质量控制薄弱处)，见表1。

表1 装配式建筑施工质量风险评估指标体系Table 1 Construction quality risk assessment index system of prefabricated buildings

图1 评估指标体系建立流程Fig.1 Establishment process of evaluation index system

2 基于区间层次分析法与模糊理论的装配式建筑施工质量风险评估模型

2.1 区间层次分析法(IAHP)

传统的层次分析法存在受主观意愿影响较强的缺陷，介于此，1994年吴育华提出区间层次分析 法(Interval Analytic Hierarchy Process，简 记IAHP)的概念。区间层次分析法是对传统层次分析法的一种改进，在建立成对判断矩阵的过程中运用数值区间代替单点数值，这样可以减弱人为主观意愿的影响，能更好地反映做出判断的不确定性。区间层次分析法的具体操作流程如下。

2.1.1 建立层次结构模型

根据评估指标体系，建立层次结构模型，本文的层次结构模型包括目标层，1级指标层及2级指标层。

2.1.2 建立成对判断矩阵

将评估指标两两对比，建立成对判断矩阵，为保证建立成对判断矩阵的可靠性，本文从从事本专业年限、职称、学历3方面对做出判断的专家进行考量，见表2。

表2 判断矩阵可靠性考量表Table 2 Reliability considerations of judgment matrix

区间层次分析法同样采用1～9标度进行量化，具体规则见表3。如果实数a为一个区间数，同时a=[a-,a+]，则可以用A=(aij)n×n表示区间判断矩阵。矩阵中元素，表示指标i相对指标j的重要程度。

表3 1～9标度量化规则Table 3 1～9 scaling rules

2.1.3 进行一致性检验

确定判断矩阵能否通过一致性检验，若不能通过，则对判断矩阵进行调整，直至通过为止，一致性检验具体方法如下：

1)计算k值、β值

2)一致性判定当k≤1，β≥1时，认为通过检验，即矩阵一致性较好；当k>1，β<1时，则认为不通过检验，即矩阵一致性较差。

2.1.4 计算评估指标权重

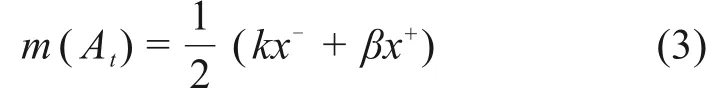
最后，需对求解的权重向量m(At)进行归一化处理，进而得到最终的权重向量如下：

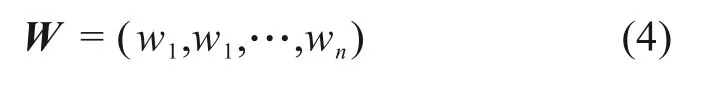
2.2 基于区间层次分析法与模糊理论的风险评估模型

影响装配式建筑施工质量的因素较多、较为复杂，同时具有一定的模糊性。介于此，基于区间层次分析法并引入模糊理论，构建装配式建筑施工质量风险评估模型，具体操作流程如下。

2.2.1 装配式建筑施工质量风险评估指标体系

本评价指标体系包含3项1级指标，19项2级指标，见表1。

2.2.2 确定装配式建筑施工质量风险评语

参考《建设工程项目管理规范》GB/T50326—2017，根据施工质量风险大小，将风险划分为5级。并结合风险等级，确定模糊分布，见表4。

表4 装配式建筑施工质量风险评语集Table 4 Quality risk assessment of prefabricated building construction

对各评估指标制定装配式建筑施工质量风险等级判别标准，见表5。

表5 装配式建筑施工质量风险等级判别标准Table 5 Construction quality risk grade criteria for prefabricated buildings

2.2.3 确定评估指标权重

基于评估指标体系，将评估指标两两对比，构造成对判断矩阵。对判断矩阵进行一致性检验，若通过则进行下一步，若不通过则需要对判断矩阵进行调整。根据判断矩阵A得到矩阵A-和A+，分别计算各矩阵最大特征根对应的特征向量，该特征向量即为权重向量，运用式(3)，对矩阵A和A+对应的权重向量进行组合，得到最终权重向量。对权重向量进行归一化处理，即得到各项指标最终权重。

2.2.4 确定隶属度矩阵

定性法与定量法是确定评价指标隶属度常用的2种方法，定量法较于定性法更加客观，本研究即采用该方法。通过构造梯形隶属度函数(见表4)确定评估指标隶属度，形成隶属度矩阵R，Ⅰ～Ⅴ等级具体隶属度函数图形，见图2。

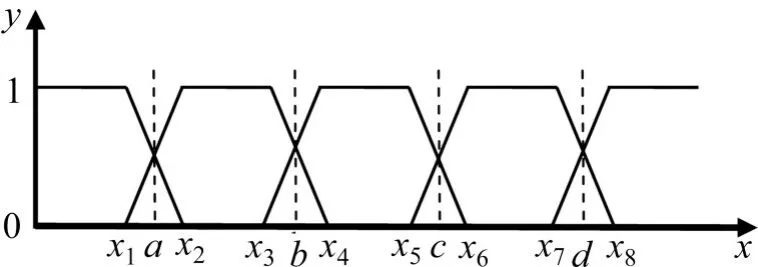
图2 梯形隶属度函数Fig.2 Trapezoidal membership function

各等级隶属度函数，见式(5)～(9)。

Ⅰ级(风险高)：

Ⅱ级(风险较高)：

Ⅲ级(风险中等)：

Ⅳ级(风险较低)：

Ⅴ级(风险低)：

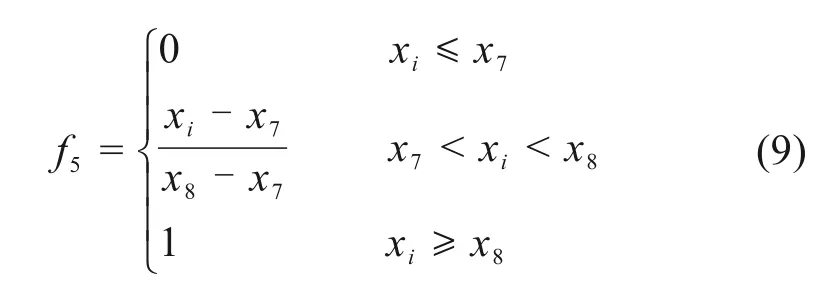
式(5)～(9)中，x1,x2,x3,…,x8取值为1,2,3,…,8。

通过计算各指标对风险等级的隶属情况，形成隶属度矩阵R，具体如下：

2.2.5 进行风险综合评估

运用权重向量与隶属度矩阵进行合成，进而得到结果向量B，具体如下：

2.2.6 结果分析并给出结论

根据最大隶属度原则，确定装配式建筑施工质量风险所处等级，并根据评估结果给出相关结论。

3 工程实例

X理工大学新校区，总建筑面积32.54万m2，包括图书馆、教学实验楼等20栋单体建筑。本工程建筑面积5 000 m2以上单体建筑的三板(楼板、内墙板、楼梯板)装配率均达到40%。本工程中需满足“三板”要求的单体，楼梯板均预制；楼(屋面)板中，除屋面、中间楼层卫生间区域，地下室顶板采用现浇板外，其余均采用预制楼板；剪力墙采用预制剪力墙板。

本工程预制装配式结构是由预制叠合楼板、预制墙板、预制楼梯板等混凝土预制构件组成，在施工现场拼装后，采用墙板间竖向连接缝现浇、上下墙板间主要竖向受力钢筋灌浆套筒连接以及楼面梁板叠合现浇形成整体的结构形式。结合本工程实际情况，展开装配式建筑施工质量风险评估，具体评估流程如下。

3.1 确定装配式建筑施工质量风险评语

根据施工质量风险大小，将风险划分为Ⅰ～Ⅴ，共5个等级，各等级具体描述见表4。

3.2 确定评估指标权重

3.2.1 建立成对判断矩阵

邀请10位从事本行业且对本工程较为熟悉的专家，基于表2对各个专家分别进行考量，综合分值分别为：9，6.5，7.6，6.5，7.6，7.2，8，8，7.6，6.1，均通过考量。各位专家根据评估指标的相对重要程度，构造成对判断矩阵，以一级评价指标Xi为例，见表6。

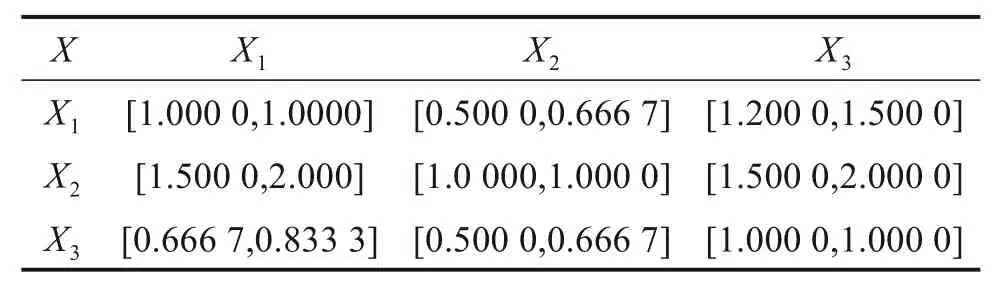
表6 X-Xi成对判断矩阵Table 6 Paired judgment matrix

3.2.2 进行一致性判定

根据表6成对判断矩阵可得到矩阵A-和A+，具体如下：

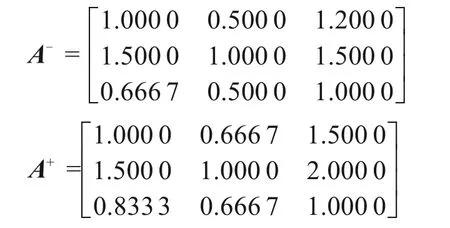
依据式(2)计算β值为1.042 2；依据式(1)计算k值为0.975 1。则满足k≤1且β≥1的条件，即矩阵有较好的一致性，通过检验。

3.2.3 计算评估指标权重

利用特征根法计算矩阵A-和A+的权重向量，具体如下：

运用式(3)计算X1，X2和X3的权重值，具体如下：

对各指标权重进行归一化处理，得到1级指标权重，具体如下：

采用同样方法，计算所有2级指标权重，见表7。

表7 2级评估指标权重Table 7 Weight of secondary evaluation index

3.3 确定隶属度矩阵

上述10位专家，根据工程实际情况，通过对现有工程资料进行整理，并依据《装配式混凝土结构技术规程》(JGJ 1—2014)、《装配式混凝土建筑技术标准》(GB/T 51231—2016)、《混凝土结构工程施工质量验收规范》(GB 50204—2015)等相关规范，对本装配式建筑施工质量风险大小做出评分，评分取0～10，具体评分结果见表8。

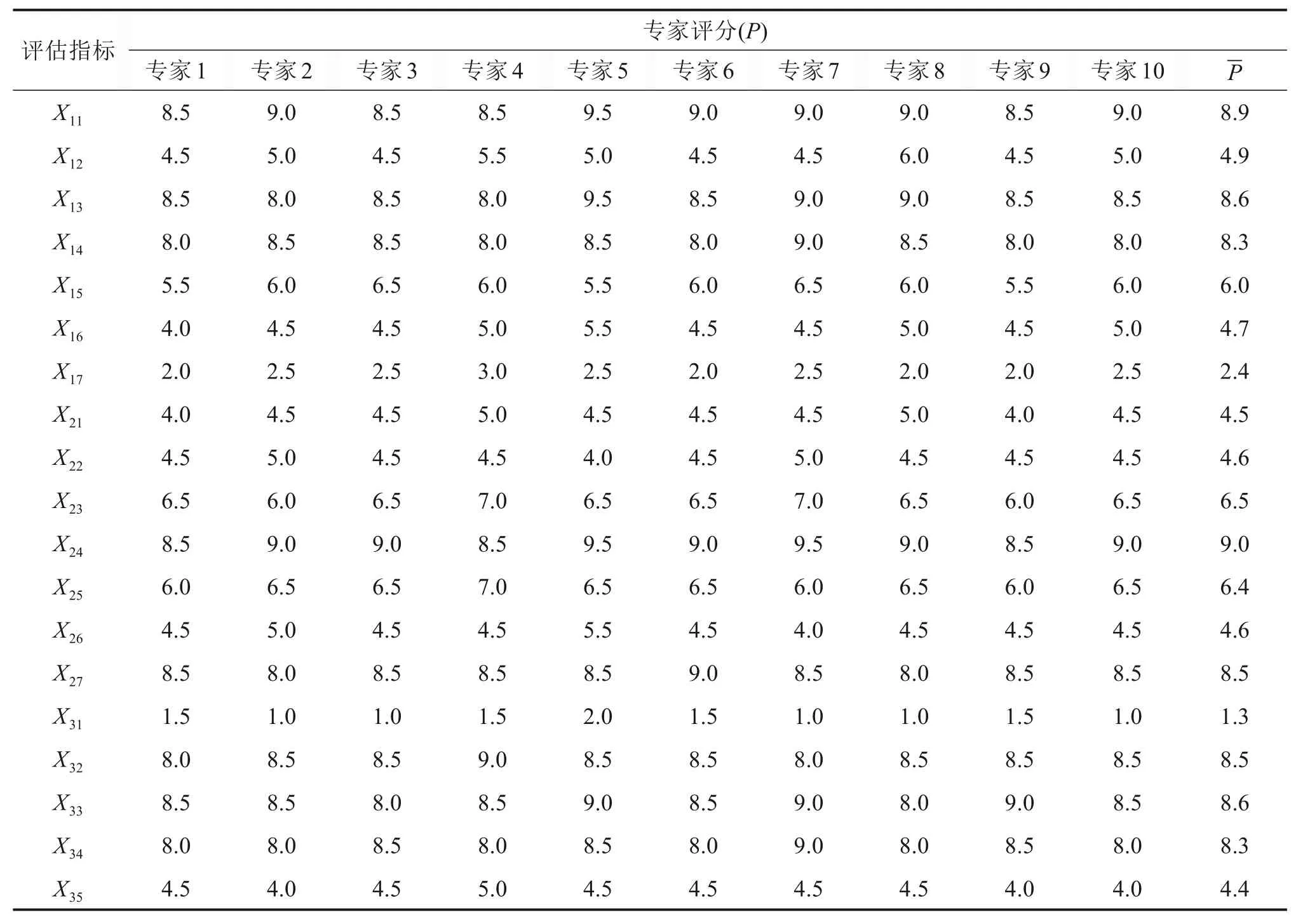
表8 专家评分Table 8 Expert scoring table

根据表8评分情况，计算各评估指标对各风险等级的隶属度，以指标X11为例。X11综合评分为8.9，代入式(8)，可知指标X11对Ⅰ～Ⅴ，5个风险等级的隶属情况分别为0，0，0，0，1，同理通过计算其他指标隶属情况，进而得到1级指标X1的隶属度矩阵R1如下：

采用同样方法，计算其他各1级指标隶属度矩阵如下：

3.4 进行风险综合评估

3.4.1 2级风险综合评估

对装配式建筑设计、构件制作及施工准备风险X1中各2级风险进行综合评估，具体如下：

对装配式建筑施工风险X2中的各2级风险进行综合评估，具体如下：

对施工完成后质量检查风险X3中的各2级风险进行综合评估，具体如下：

3.4.2 1级风险综合评估

对装配式建筑施工质量总体风险X进行评估，具体如下：

3.5 评估结果分析

根据最大隶属度原则可知，1级风险中，装配式建筑设计、构件制作及施工准备风险X1所处等级为Ⅴ(风险低)；装配式建筑施工风险X2所处等级为Ⅲ(风险中等)；施工完成后质量检查风险X3所处等级为Ⅴ(风险低)；项目总体风险为低，从风险整体分布可以看出，为中等偏低状态。

4 结论

1)通过文献研究并听取专家建议的基础上，对装配式建筑施工质量风险进行识别，并建立装配式建筑施工质量风险评估指标体系。本评估指标体系相对完善，指标设置较为合理，具有一定的参考价值。

2)引入区间层次分析法确定各指标的相对重要度，该方法可以很好地解决指标间相对重要程度较为模糊的问题，使计算的权重更加准确。通过构造隶属度函数的方式确定指标对风险等级的隶属情况，简便快捷。本文基于区间层次分析法与模糊理论，构建了装配式建筑施工质量风险评估模型。

3)运用基于区间层次分析法与模糊理论的装配式建筑施工质量风险评估模型，对X理工大学新校区装配式建筑施工质量进行风险评估，得出项目总体质量风险处于偏低状态的结论，施工质量风险总体可控。虽然风险总体处于中等偏低状态，但仍不能掉以轻心，从设计、施工到施工完成后的质量检查仍需要严格的按照规范执行，建立完善的质量监督管理制度，密切关注个质量控制点，进而实现问题早发现、早控制、早解决。

4)通过实例研究验证了模型的合理性与可靠性，同时风险评估结果可以作为质量控制的重要依据。