考虑风险的国际集装箱多式联运路径选择研究

冯芬玲，孔祥光，吴庆芳

(中南大学 交通运输工程学院，湖南 长沙 410075)

国际集装箱多式联运作为一种高效的运输组织形式，把多个运输方式整合起来，使得运输全程形成一条完整的运输链。近年来，随着“一带一路”倡议的推进及国际贸易合作的加深，国际货物运输行业发展迅速，国际集装箱多式联运逐渐成为国际物流活动的重要形式，研究国际集装箱多式联运路径选择问题具有重要的理论和现实意义。由于运输距离长、涉及范围广、中间环节多等特点，国际集装箱多式联运作为一个较复杂的系统，在运输过程中会面临着各种各样的不确定风险，而且一旦发生事故则会造成较大的经济损失，其安全问题不容忽视。在研究国际集装箱多式联运路径选择时加入对运输风险的考量，有利于提高运输可靠性，促进国际集装箱多式联运系统的安全、稳定运行。在集装箱路径优化模型研究领域，学者们主要从影响路径选择的关键因素入手，以影响因素中的一个或多个为决策目标构建单目标或多目标优化模型，例如，刘维林[1]构建了运输成本最小化的单目标模型来研究天津至墨西哥的集装箱多式联运路径优化问题，ZHAO等[2−3]基于海铁联运网络提出了总成本最小的集装箱路径规划模型，RESAT等[4−6]以成本最小和时间最小作为模型的目标函数，CHEN等[7]建立了最小化运输时间、运输成本和集装箱使用成本的多目标规划模型，SUN等[8−10]在优化目标中增加了碳排放因素来研究低碳环境下的集装箱多式联运路径优化问题，HAO等[11−12]将集装箱多式联运服务质量也作为模型的优化目标之一。通过对大量文献的阅读和总结发现，现有研究中的集装箱多式联运路径优化模型多以成本、时间作为优化目标，近年来也有不少学者考虑环境保护和服务水平等影响因素，将碳排放、服务质量、客户满意度等加入到优化目标中去，但很少有学者会在优化模型中考虑到联运风险的影响，刘清等[13]虽在研究长江干线集装箱多式联运路径优化问题时考虑了运输风险，但运输风险的度量采用的仅是个人主观赋予的相对值，没有具体的风险值测算依据。本文将构建国际集装箱多式联运风险评价指标体系，把突变级数法应用于多式联运风险的量化上，然后将联运风险纳入路径选择模型中，建立以运输费用、时间、风险和综合能耗为综合优化目标的国际集装箱多式联运路径选择模型，以期实现国际集装箱多式联运经济性和安全性的综合最优。

1 多式联运风险评估

国际集装箱多式联运风险是指集装箱货物在国际多式联运过程中受到某些因素影响而发生事故造成货损的可能性，由路段运输风险和节点换装风险加和求得。国际集装箱多式联运面临的内外部环境复杂多变，具有较强的突变性，故本文选择以突变理论为基础的突变级数法来计算联运风险。国际集装箱多式联运风险的具体计算步骤如下。

1.1 风险评价指标体系构建

分析集装箱在路段运输和节点换装的风险影响因素，筛选出1级和2级评价指标，并通过两两比较的方式确定指标的相对重要性排序，分别构建路段运输风险评价指标体系和节点换装风险评价指标体系，如图1所示，其中位置靠左的指标的重要性相对更高。

图1 国际集装箱多式联运风险评价指标体系Fig.1 Risk evaluation index system of international container multimodal transport

1.2 评价指标归一计算

突变模型分为多个类型，不同突变类型的状态变量和控制变量的数量不同[14]。本文研究中所涉及到的突变模型包括尖点突变、燕尾突变和蝴蝶突变，这3个突变模型对应的控制变量分别为2个、3个和4个。不同突变模型对应的归一公式也有所不同，根据相符的突变模型选择对应的归一公式进行计算。例如，1级指标自然环境因素下设有2个2级指标，构成尖点突变模型；人员管理因素下设有3个2级指标，则构成燕尾突变模型。

通过邀请国际集装箱多式联运相关领域的10位专家对各2级指标打分，并与搜集到的不完整的客观信息和数据进行对比、修正，得到2级指标初始值a，b，c，d，再根据归一公式计算出其突变级数值，然后取2级指标突变级数值的平均值作为1级指标的初值。

1.3 风险值计算

突变级数法是通过逐级向上递归进行运算的，本文以求出的总突变隶属函数值作为风险值。路段运输风险评价下设有4个1级指标，构成蝴蝶突变模型，采用蝴蝶突变的归一公式向上递归计算得出路段运输风险值；而节点换装风险则采用燕尾突变的归一公式向上递归计算得出。

2 路径选择模型建立

将国际集装箱多式联运路径选择问题描述为：有一批集装箱货物需要从国内某城市O运送到国外某城市D，中间有n个城市，可从其中选择若干个城市作为途径节点，每相连的2个城市节点之间存在多种运输方式可供选择，选取运输费用、运输时间、综合能耗和运输风险作为集装箱运输路径及其运输方式选择的决策目标。该问题的假设条件包括：1)同一批货物在运输过程中不可分割；2)货物在2个节点之间至多只能选择一种运输方式；3)货物在每个节点上至多转换一次运输方式；4)节点和路段的容量均可满足运输需求；5)不考虑货物的通关时间和铁路换轨时间。

2.1 相关参数及变量说明

i：多式联运网络中的城市节点，i=1,2…,n；k,l：运输方式，取值为1,2,…,m，k≠l；α：取值为1或2，α=1表示国内段运输，α=2表示国外段运输；Q：货物运输量；：货物从i节点到i+1节点采用k运输方式时的运输距离；：货物从i节点到i+1节点采用k运输方式时的运输基价1；：货物从i节点到i+1节点采用k运输方式时的运输基价2；：货物在i节点由运输方式k转换为l时的单位换装成本；vk：运输方式k的行驶速度；：货物在i节点由运输方式k转换为l时的单位换装时间；ek：货物采用k运输方式时能源的单位消耗量；ek,l：货物由运输方式k转换为l时能源的单位消耗量；：货物从i节点到i+1节点采用k运输方式时的路段运输风险；：货物在i节点由运输方式k转换为l时的换装风险；：0-1变量，判断货物是否从i节点采用k运输方式运送到到i+1节点；：0-1变量，判断货物是否在i节点由运输方式k转换为l；zi,i+1：0-1变量，判断货物从i节点到i+1节点属于国内段还是国外段运输。

2.2 模型构建

1)目标函数

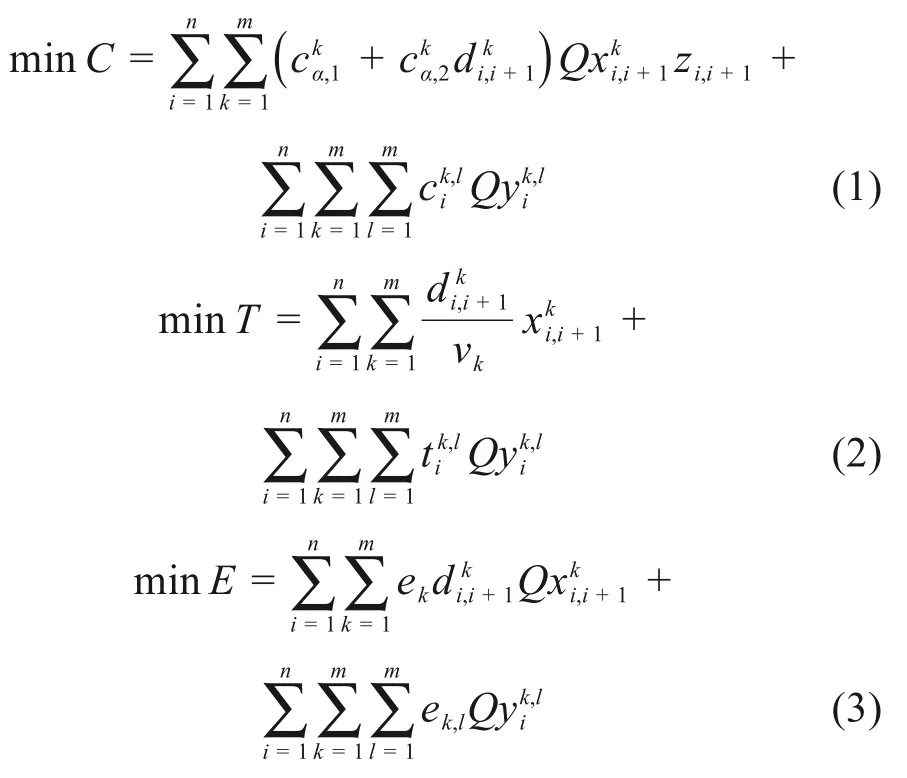
2)约束条件

式(1)～(4)分别为运输费用、运输时间、综合能耗和运输风险的函数；式(5)保证运输过程的连续性；式(6)保证2节点之间只能选择一种运输方式；式(7)保证同一节点上只能进行一次运输方式的转换；式(8)定义了决策变量为0-1变量；式(9)表示集装箱运输量不能为负数。

3 算例分析

3.1 算例介绍与相关数据

本文选取长沙为国际集装箱多式联运的始发城市，德国柏林为终点城市，综合考虑亚欧大陆桥、传统海运、瓜达尔铁海联运、西部陆海新通道、东盟通道等多个运输通道，选取了武汉等25个城市作为中间节点。设定有10个20英尺的集装箱(配货毛重17.5 t)将从长沙运往柏林，每相连2个城市节点之间有铁路、公路、水路中的1～3种运输方式可供选择。该算例的集装箱多式联运网络如图2所示。通过查阅网站、官方文件、专家打分以及参考文献[9,12]搜集得到所需算例数据，部分原始数据或经初步处理过的数据如表1至表4所示。

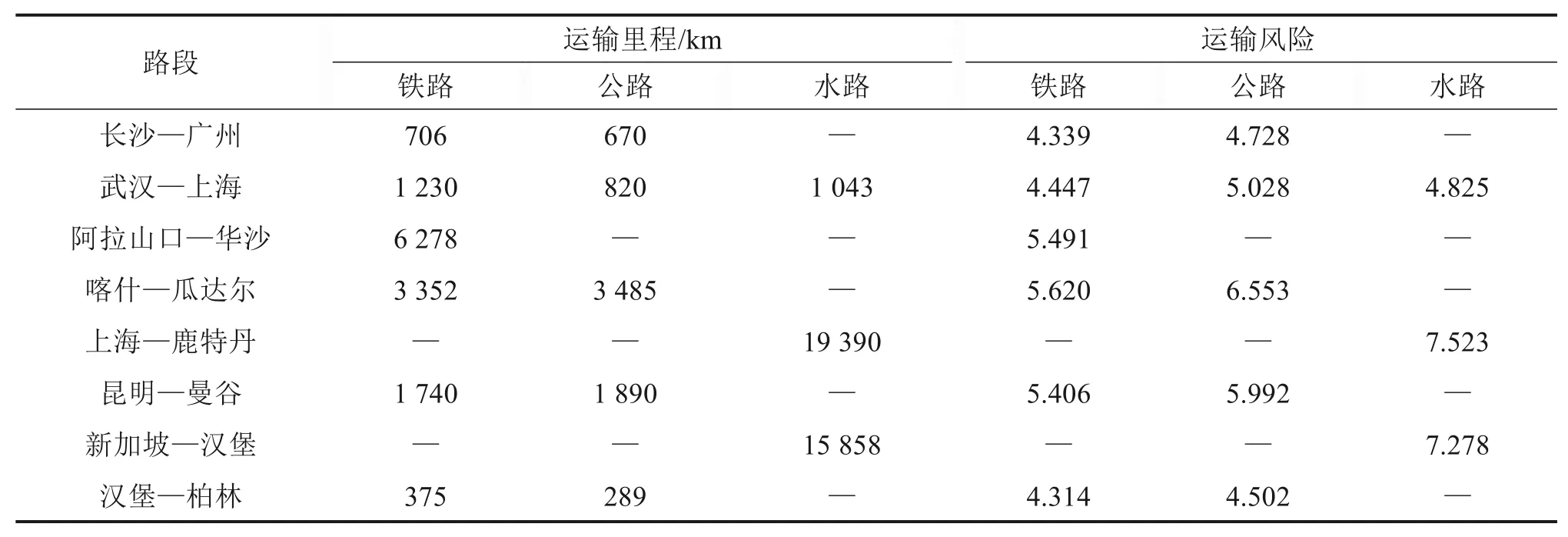
表1 部分路段运输里程及运输风险Table 1 Transport distance and risks of part of the route

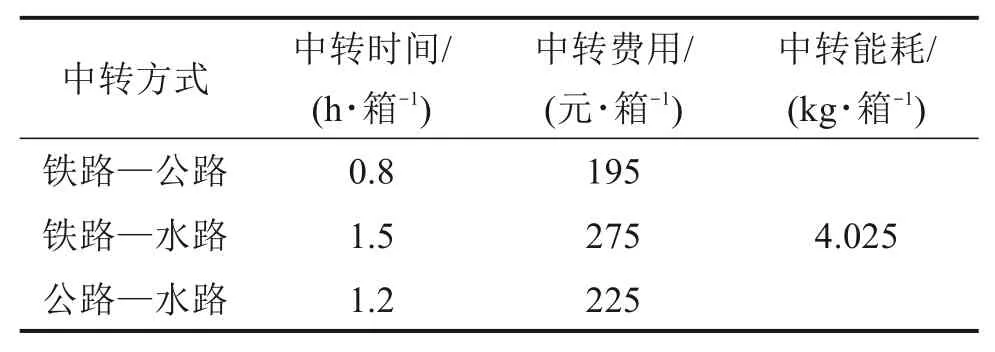
表4 中转时间、费用及能耗Table 4 Transit time,cost and energy consumption

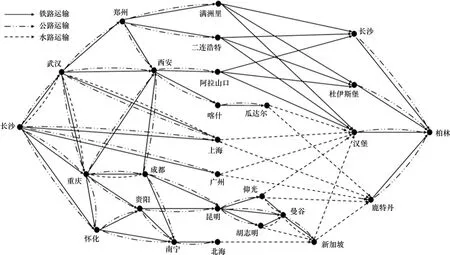
图2 长沙至柏林集装箱多式联运网络Fig.2 Container multimodal transport network from Changsha to Berlin

3.2 结果及分析

参考文献[15]所设计的遗传算法，分别以运输费用最低、运输时间最短、综合能耗最少、运输风险最小、4个目标综合最优为决策目标对算例进行求解，结果如表5所示。当决策目标发生变化时，长沙—柏林的集装箱多式联运最优路径及运输方式也会不同。由于水路运输的单位成本和能耗均低于其他运输方式，所以在以运输费用最小和综合能耗最小分别作为决策目标时，求得的最优运输方案是相同的。

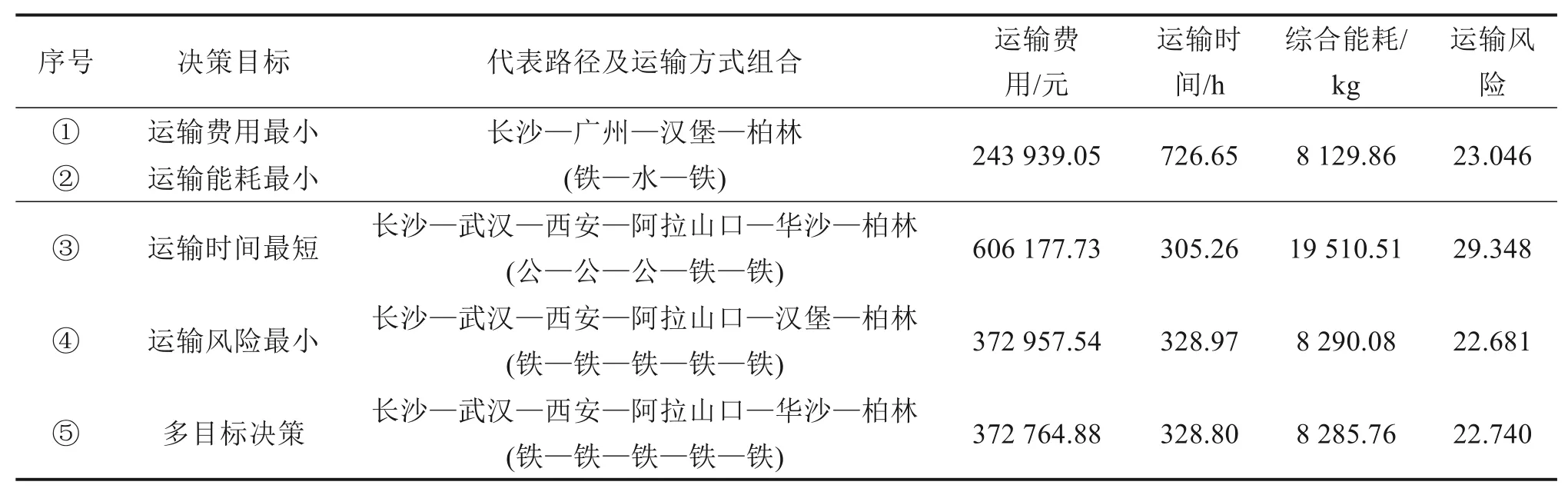
表5 不同优化目标下的最优方案及目标函数值Table 5 Optimal schemes and objective function values under different optimization goals

1)多目标优化结果有效和可行

不同优化目标下求得的各运输方案的运输费用、运输时间、综合能耗和运输风险值的对比情况如图3所示。通过对比分析可知，水路运输虽能降低运输费用和综合能耗，但由于行驶速度慢及航行距离远，从而使得集装箱运输时间过长，结果①的运输时间约为结果⑤的2.2倍；公路运输虽能在一定程度上降低运输时间，但其费用、能耗及风险均较高，从图3中可以看出，结果③的运输费用、综合能耗和运输风险都明显高于其他几个运输方案；多目标优化结果⑤较好地降低了运输费用，缩短了运输时间，减少了综合能耗，同时也在一定程度上降低了运输风险，从而能够实现综合效益的最优。

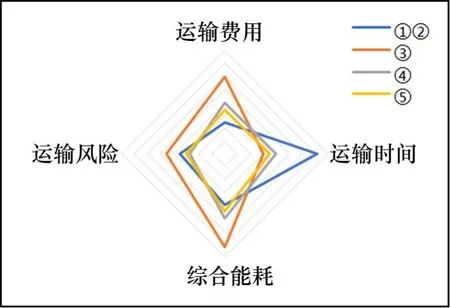
图3 各运输方案的费用、时间、能耗及风险对比Fig.3 Comparison of cost,time,energy consumption and risk of each transportation plan

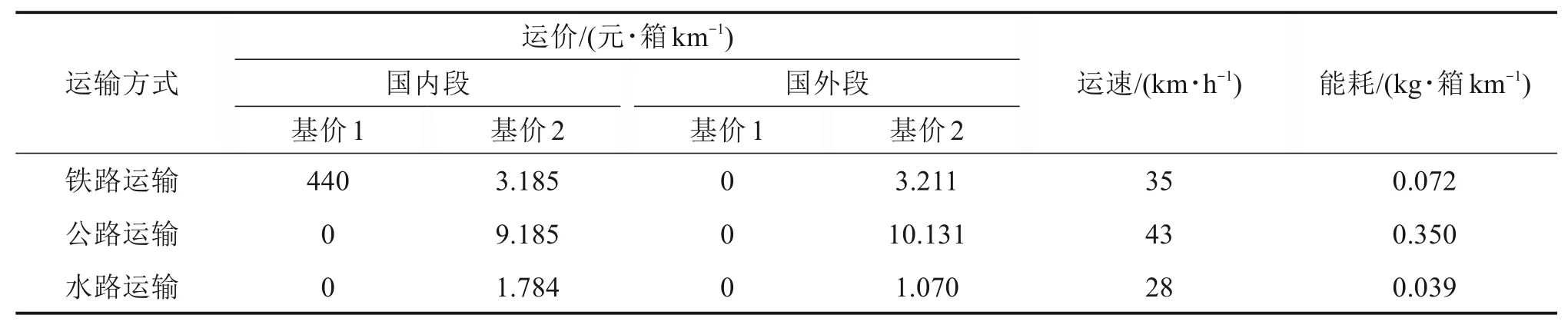
表2 各运输方式的运价、运速及能耗Table 2 Price,speed and energy consumption of each mode of transportation

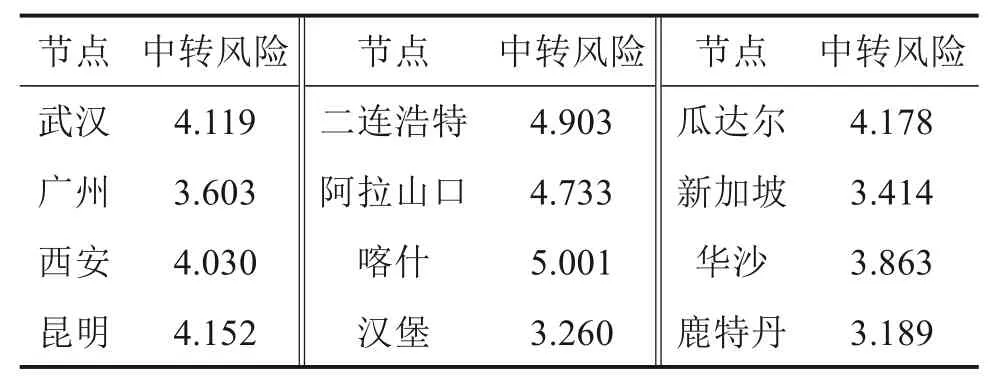
表3 部分节点中转风险Table 3 Transit risks on the part of nodes

2)不同决策者的偏好路径有所差异

国际集装箱多式联运的参与者较多，由于不同多式联运参与者的偏好不同，当他们分别作为决策者时所可能选择的运输方案也会有较大差异。若决策者为政府，相比经济效益，会更多关注运输过程中的节能效应，所以会偏好于综合能耗最小的路径，如结果②。若决策者为托运人，运输费用和运输时间将会被优先考虑，其次考虑的是运输过程中的安全性，综合能耗对其决策没有影响；若决策者为多式联运经营者，将更多追求的是经济利益，会优先考虑运输成本、时间和风险，并对综合能耗有一定程度的关注。由于托运人和多式联运经营者的偏好相似，他们可能都更偏向于选择结果⑤代表的运输路径。

3)不同品类货物的优势路径不同

由于自身价值和时间价值等特性的差异，不同品类货物可选择的最优运输路径也会不同。以中欧贸易为例，参考中欧班列的去程货物，将中欧贸易货物品类及其特性进行归纳分析如表6所示。电子产品类货物由于时效性要求高，自身价值也较高，适合选择运输时间较短、风险较小的路径，如结果④或⑤；机械家电类货物的销售周期较长，市场需求较为稳定，则可以选择运输费用较低的路径，如结果①；而日用百货类货物的自身价值较低，对运输时间的要求也不高，结果①、④和⑤均可以作为其运输的备选路径参考。

表6 中欧贸易货物分类及其特性Table 6 Classification and characteristics of goods in China-Europe trade

4)中欧班列在中欧贸易中优势明显

多目标优化结果⑤的路径及运输方式组合与现行的中欧班列几乎重合，这也从侧面验证了中欧班列的优越性和可行性。相比结果①和②，结果④和⑤的运输费用和综合能耗虽略高，但其运输时间却大大缩短，运输风险也有所降低；与结果③相比，结果④、⑤的运输费用、综合能耗和运输风险都远低于结果③，但其运输时间并没有相差太多，结果③仅比结果④、⑤节省了约一天的时间。综合来看，中欧班列具有成本低、能耗少、速度快、风险小等优点，相比其他运输路径和运输方式的竞争优势较为突出。

5)不同运输通道的经济与安全水平差异显著

长沙—柏林有多个运输通道可供选择，不同运输通道的经济效益与安全水平差异明显。各选择一条运输路径代表其所属的运输通道，求解各运输通道代表路径的运输费用、运输时间、综合能耗、运输风险的值，如表7所示，并对比如图4所示。

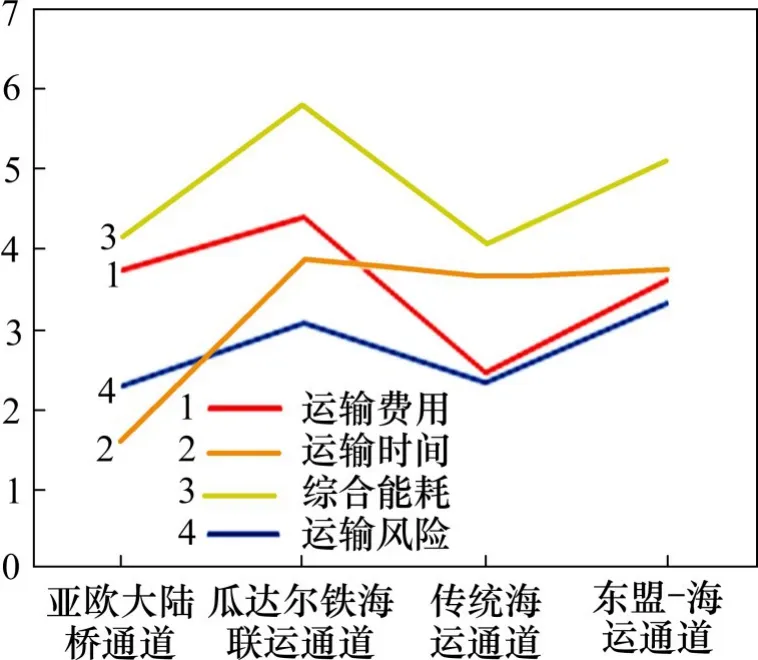
图4 各运输通道的经济与安全水平对比Fig.4 Comparison of economic and security levels of each transportation channel

表7 不同运输通道代表路径的费用、时间、能耗及风险值Table 7 Values of cost,time,energy consumption and risk of the representative route of each transportation channel

亚欧大陆桥通道在运输时间和风险方面的优势最大，运输费用和综合能耗也都处于中间或偏低水平，综合效益在4个运输通道中最高；瓜达尔铁海联运通道虽然缩短了中国与西亚地区间的运输距离，但其途径自然条件较为恶劣的青藏高原地区，且在中欧运输中路径迂回，造成其运输费用、时间、能耗和风险均较大，在中欧贸易中几乎没有竞争优势；传统海运通道的运输费用和综合能耗最低，运输风险较小，运输时间却比亚欧大陆桥通道高了近131%；由于东南亚地区的道路条件及社会秩序相对较差，东盟—海运通道的运输风险最高，运输费用、时间和能耗的优势也很小，故其在中欧运输中的竞争力薄弱。

4 结论

1)国际集装箱多式联运面临的情况复杂多变，某一影响因素发生变化都可能造成严重后果。本文构建了国际集装箱多式联运风险评价指标体系，将突变级数法应用于联运风险的量化评估，并在路径选择模型中加入了对运输风险的考量，旨在实现运输费用、时间、能耗和风险的综合最优，保证国际集装箱多式联运经济效益的同时，提高国际集装箱运输的安全性。

2)在从长沙至柏林的算例中，综合考虑了亚欧大陆桥、传统海运通道、瓜达尔铁海联运通道、西部陆海新通道、东盟通道等多个运输通道，更好地丰富了途径节点和路段备选集，使得算例更加贴近实际。

3)算例求解结果符合预期，相比单一目标优化结果，多目标优化方案较明显地缩短了运输时间，降低了费用、能耗和风险，能够有效地为国际集装箱多式联运路径选择提供参考。同时，求解了不同优化目标下的运输方案，能够为不同运输需求或不同品类货物的国际集装箱多式联运提供相应的路径参考依据。此外，求解结果也从侧面验证了中欧班列在中欧集装箱运输竞争中具有较为突出的优势。

4)由于当下一些外部因素对国际运输的影响，导致其稳定性相对较差，真实稳定的班期数据不易获取，而本文侧重于研究常态化的国际集装箱多式联运情景，故在模型中暂未考虑铁路列车和轮船的班期限制，即未考虑由于班期原因造成的在节点上的等待时间和堆存费用等。若后续能够获取真实稳定的班期相关数据，则可将班期限制加入到模型中进一步研究。