高速铁路路基B组填料振动压实参数优化室内试验研究

叶阳升，陈晓斌，惠潇涵，蔡德钩，尧俊凯，金亮星

(1.中国铁道科学研究院集团有限公司，北京 100081；2.中南大学 土木工程学院，湖南 长沙 410075；3.中南大学 重载铁路工程结构教育局重点实验室，湖南 长沙 410075；4.中国铁道科学研究院集团有限公司 铁道建筑研究所，北京 100081)

高速铁路路基填料以粗粒土为主，具有强度高、稳定性好的特性，其压实质量是确保高速铁路路基平稳运行的关键因素。振动压实法是路基填筑的常用方法[1]，具有效率高、稳定性好、传播深度深等优点。已有研究表明，选择合理的振动参数能使粗粒土填料达到最佳密实状态；而颗粒破碎是粗粒土的基本特性之一，在振动压实作用下,由于粗颗粒骨架点接触的特点容易造成颗粒破碎现象[2]，粗颗粒间主要以点接触为主，在振动压实作用下，由于应力集中更加容易发生颗粒破碎现象，从而导致粗粒土的变形和强度特性发生改变，引发沉降变形、翻浆冒泥等工程灾害。故有必要开展路基填料振动压实特性及颗粒破碎演化规律研究，为高速铁路路基的填筑作业提供技术参考及试验依据。目前，针对粗粒土压实特性的研究主要包括2个方面[2]，一是填料本身特性，包括级配、含水率、母岩强度等，二是振动参数的选取即频率、幅值、激振时间。针对填料本身特性，冯瑞玲等[4]对8种不同级配的粗粒土展开振动压实试验研究，发现级配特性对粗粒土的压实效果有很大影响，级配良好的土有着更好的压实效果。吴二鲁等[5]通过对16组不同级配粗粒土进行表面振动压实试验，引入级配曲面面积指标对压实效果进行评价，并依次确定了粗粒土的最优级配区间及对应级配曲线面积。杜俊等[6]对多个级配不同含水率的粗粒土进行击实试验，研究了粗粒含量、含水率对干密度及颗粒破碎率的影响规律；近年来，随着智能压实技术(IC)的提出，更多的学者针对振动压实参数优化展开研究，WERSÄLL等[7−8]研究了振动压路机工作频率对碎石材料的影响，结果表明振动压路机在接近共振的频率下工作压实效果最好且更加省时、节能。黄强[9]通过表面振动压实试验确定了粗粒土合理振动压实时间为3 min。COMMURI等[10]提出了一种基于神经网络的沥青压实分析仪的方法，能够连续预测施工过程中的密度变化；AN等[11]提出了一种基于遗传算法对压实参数动态优化方法，能够有效提高压实效率，但优化过程需要大量的样本数据进行机器学习。由于现场测试的复杂性，南兵章等[3,12−14]根据自主研制的可调频调幅室内振动压实仪，先后研究了振动参数对粉土、砂土、水泥稳定碎石、土石混合料等填料的压实特性，确定了静压力、激振力、振幅和频率对填料干密度的影响规律，并验证了室内振动压实仪的可行性。HUANG等[15]通过图像处理技术发现多孔沥青混凝土(PAC)在振动压实过程中上部最先压实，并发现振动频率过大容易导致粗颗粒破碎。路基填料的压实性能是路基沉降控制的关键指标，而影响填料压实性能的参数非常复杂。目前对于不同类型的路基填料，尚未有广泛适用的研究结论，需要针对具体材料具体特性开展针对性研究。对于高速铁路B组填料这种特殊填料的振动压实特性亟待开展专门试验研究。本文采用室内振动压实仪模拟现场压路机的实际碾压过程，分析了振动频率、激振荷载、振动次数等因素对高速铁路B组填料粗粒土的干密度和破碎特性的影响，基于振动压实机理对试验结果进行了探讨，并确定了高速铁路B组填料粗粒土的合理振动参数范围。研究结论可为高速铁路B组填料粗粒土现场碾压作业提供理论依据和技术参考。

1 试验材料及方案

1.1 试验材料

试验材料取自某高铁路基B组填料，为保证试验土样级配与现场一致，通过对现场取得的200 kg填料进行颗粒筛析，得到现场基床底层填料级配，但由于试验筛析出来的最大粒径为60 mm，超过了室内压实筒的所允许的最大粒径，根据《铁路工程土工试验规程》需剔除粒径大于40 mm的颗粒，通过左永振等[16]对4种缩尺方法适用性探讨结果，等量替代法具有保持原有粗粒、细粒含量不变的优点，适合超径含量小于40%的粗粒土填料。故选取等量替代法对现场填料进行缩尺，缩尺方法见式(1)，缩尺后级配如图1所示，图中，P为小于某粒径的颗粒含量，d为粒径。

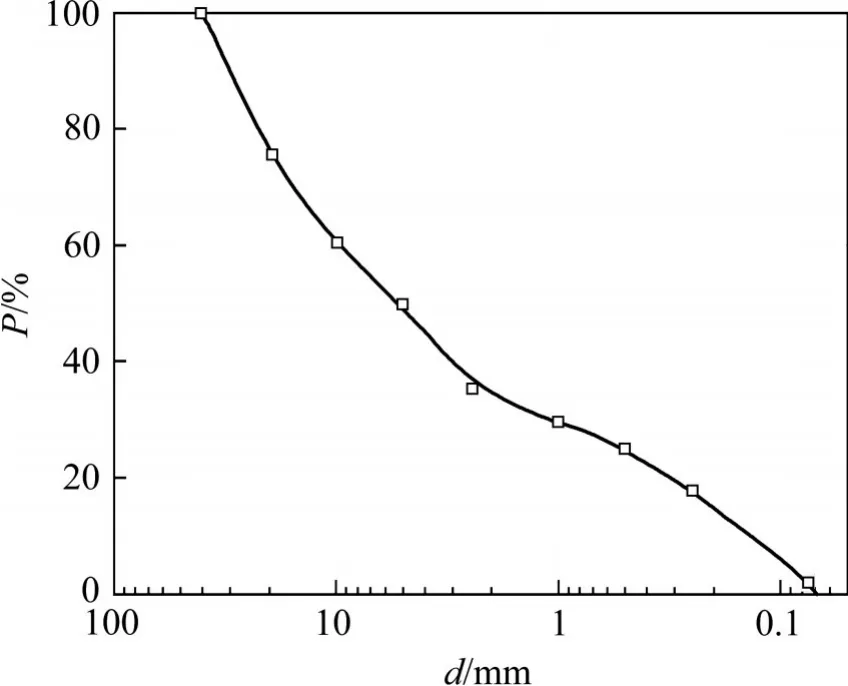
图1 试验材料级配曲线Fig.1 Gradation curve of tested materials

式中：Pi为剔除后某粒组含量；Poi为原级配某粒组含量，%；Pdmax为超径颗粒含量，%；P5为大于5 mm粒径土含量，%。

1.2 试验方案

试验采用室内振动压实仪，能够充分模拟现场振动压路机碾压过程。为分析频率f，名义振幅A0，振动次数n等参数对粗粒土压实特性的影响，设计5种频率、3种振幅下共15种组合工况，并记录压实过程中干密度随振动次数变化值。具体试验工况如表1所示。文中采用的振幅为名义振幅，即将压路机的钢轮悬空所计算的振幅，计算公式如式(2)所示。

表1 试验方案Table 1 Testing programs

式中：A0为名义振幅；MP为参振质量；md为偏心块质量；e为偏心距。

2 振动压实参数对粗粒土压实性能的影响

2.1 振动频率−干密度关系

为了分析振动频率对材料压实特性的影响，整理了不同振幅下的频率与干密度的试验结果，如图2所示。

通过图2可以看出，4种振幅下干密度随频率变化的趋势保持一致，其变化趋势可以分为3个阶段：1)缓慢增加阶段，当名义振幅A0较小时，粗粒土填料在激振频率为10～20 Hz区间内缓慢增加，当名义振幅A0较大时，粗粒土填料在激振频率为10～15 Hz区间内缓慢增加，这是由于当激振频率较低时，颗粒保持在初始位置振动，导致细颗粒不能充分填满孔隙。2)迅速增加阶段，粗粒土填料干密度随激振频率迅速增加，粗粒土填料振动响应明显，细颗粒易偏离初始位置能够充分填满孔隙，土体结构逐渐密实。同时当振幅较大时由于振动强度增加填料在较低频率便能进入迅速增加阶段。3)最优振动频率阶段，此阶段相比低频压实，土体结构更加密实，干密度随激振频率增加的变化逐渐变缓，但存在一最优频率使得干密度出现最大值，此时激振频率接近粗粒土填料的固有频率，从而引起共振现象，提高振动压实效果，使得粗粒土填料达到最佳密实状态[9]，并确定试验土样最佳振动频率为25～30 Hz，这一结果与现场压路机作业的振动频率[17]一致，说明试验所用仪器能很好的模拟现场压路机碾压作业。

图2 不同振幅下频率与干密度间关系Fig.2 Relationship between frequency and dry density with different amplitude

同时分析频率和振幅对干密度影响程度的敏感性，以频率为25 Hz为例，压实后干密度随幅值变化依次为4.8%，1.0%；以幅值为0.3 mm为例，压实后干密度随频率变化依次为3.6%，4.1%，9.7%，1.7%，由此可见，频率对压实后干密度的影响更大。

2.2 激振荷载−干密度关系

土体在有限空间内发生剪切破坏颗粒重新排列的过程，就是土体密实的过程[18]。粗粒土振动压实过程可以简化为，土体受到循环作用的激振力，引起循环剪切应力，使土体发生周期性颗粒重新排列而压实的过程。

激振力是由2个对称分布的偏心块高速旋转的离心力带动激振头上下运动所产生。激振力与振动频率、偏心块质量、偏心距有关，具体计算公式如式(3)所示[19]。

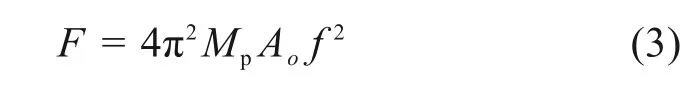
式中：F为激振力；f为激振频率。

施加到土体上的激振荷载Ps如式(4)所示，得到激振荷载与干密度间关系，如图3所示。

图3 激振荷载与干密度间关系Fig.3 Relationship between excitation force and dry density

式中：S为激振头与击实筒的接触面积。

根据图3结果可以看出，当振动频率在10～30 Hz区间时，随着激振荷载的增加干密度存在一包络区域。处于上包络线上对应此激振荷载作用下最优振动频率，相反下包络线代表激振荷载的振动频率最低值。以Ps=50 kPa为例，可以看出，在包络区域内，试样干密度由大到小对应的频率依次为25，30，20和15 Hz，使得干密度最大频率恰好处于最优频率区间25～30 Hz。

对比水平向关系可以看出，干密度随激振荷载的增加呈“S”型增长，即缓慢增加−迅速增加−趋于平稳3个阶段，“S”型曲线的2个拐点分别记为第1临界荷载(CL1)和第2临界荷载(CL2)。以下包络线为例，第1临界荷载CL1约为20 kPa，当激振荷载小于此临界荷载时，此时粗粒土填料受到的动应力较小，颗粒振动响应较弱，此时压实主要是由于静载作用。当激振荷载大于第1临界荷载CL1时，颗粒振动响应增强，使得土颗粒之间相互摩擦减小，填料能够得到有效压实；当激振荷载继续增大超过第2临界荷载L′2时，约为110 kPa，此时土体已达到稳定密实结构，干密度的增长趋于平稳，且由于荷载较大，粗颗粒容易发生破碎导致填料级配发生改变。对于上包络线往往在较小的激振荷载下便能达到稳定密实结构，这是由于填料的固有频率与振动频率接近，发生共振现象，使得实际振幅增大，颗粒间更加容易发生重新排列。

综上所述，确定路基填料最优振动参数时，需同时满足2个条件：1)振动频率为土体最优振动频率，2)激振荷载需大于第2临界荷载。

2.3 振动次数—干密度关系

为了研究振动次数对土体压实特性的影响，对振动次数与干密度的试验数据进行了分析。压实过程中干密度随振动次数变化如图4所示，具体划分标准如图5所示。

图4 不同频率下振动次数与干密度间关系Fig.4 Relationship between vibration times and dry density with different frequencies

粗粒土填料在不同频率压实过程中干密度变化随振动次数均呈现对数增长，压实速率随干密度的增加逐渐变缓。对比不同频率压实稳定所需振动次数，发现当频率越大所需振动次数越多，这是由于频率较大时往往能够达到较大干密度，所需能量增加，故需要更多振动次数。当振动频率为最优振动频率区间时，即f∈[25 Hz,30 Hz]时，合理振动次数n应为[2 500,5 000]，对应振动时间t为100～200 s之间。

图5中还显示出不同振动频率下干密度与振动次数增加关系存在相同趋势，故对不同振动频率下压实阶段进行统一划分。首先对振动次数和干密度做归一化处理，计算公式如式(5)和式(6)。

式中：i为当前压实状态；Δρi为i状态的干密度增量；Δρmax为干密度最大增量；记为i状态的相对干密度；ni为i状态的压实次数；nmax为压实稳定时最大压实次数；记为i状态相对压实次数。

归一化处理后不同压实频率下，相对干密度ρ*与相对压实次数n*关系如图5所示。

图5 不同频率下n*-间关系Fig.5 Relationship between n*andwith different frequencies

根据图5，不同压实频率下相对干密度ρ*随相对压实次数n*增长均呈线性−非线性−线性的增长规律。根据ρ*将压实过程分为3个阶段。当ρ*＜0.6时，为阶段Ⅰ，此阶段相对干密度与相对振次间呈快速线性增加。此时，材料结构松散，没有形成牢固的骨架，抵抗整体变形的能力主要由颗粒间摩擦力提供。由于此时激振力产生的剪应力大于填料变形抗力，故振次与干密度能保持线性关系，并迅速将填料压密；当0.6≤ρ*＜0.9时，为阶段Ⅱ，此阶段材料结构逐渐密实，颗粒间摩擦力逐渐增大并且逐渐形成牢固的骨架。此时填料抵抗变形的能力逐渐增加，ρ*随n*的变化速率逐渐变缓，振次与干密度的关系逐渐由线性向非线性转变；0.9≤ρ*时，为阶段Ⅲ，此阶段相对干密度与相对振次间呈缓慢线性增加，材料结构达到相对密实状态，干密度变化趋于平稳。激振力产生的剪应力已难以克服颗粒间摩擦力以及颗粒骨架间的支持力，振次与干密度关系的非线性减弱，干密度极少量增加，看作是由于粗粒土在振动压实作用下发生颗粒破碎，破碎后的细颗粒进一步填充了粗粒土骨架孔隙，造成密实度增加[20]。

3 颗粒破碎对粗粒土压实性能的影响

3.1 级配演化特性

统计粗粒土在不同激振频率下振动压实后级配如图6所示，根据级配曲线可以看出击实后各粒径筛孔的通过率皆呈增大趋势，并且随着频率的增加，级配的变化程度也逐渐增大。

图6 不同频率下振动压实前后级配曲线Fig.6 Gradation curves before and after vibration compaction with different frequencies

级配的改变引起各粒径组质量同样发生改变，为分析频率对级配变化的影响，引入质量变化率(RMC)对各粒径含量变化展开分析，RMC计算公式如式(7)所示，其中RMC为正值代表颗粒含量增加，RMC为负值代表颗粒含量减少。

式中：Mi为击实后某粒组含量，g；Moi为试验级配某粒组含量，g。

根据图7结果显示，当频率为10 Hz时，此时频率较低各粒径RMC值变化均比较小，主要是由于频率较低时，所受到的峰值应力较低，颗粒很少破碎。当振动频率为15～30 Hz时，试样在压实前后各粒径含量均出现明显变化，对于20～40 mm颗粒RMC值均为负，且随频率的增大RMC值逐渐减小；10～20 mm和5～10 mm粒径组范围内RMC值均为正，即破碎造成的质量损失小于由较大粒径组破碎增加的质量，故而导致颗粒含量增加；同理2～5 mm间RMC值为负，即破碎造成的质量损失大于由较大粒径组破碎增加的质量，故而导致颗粒含量减小；而对于小于2 mm颗粒，可以看出RMC值趋于一个稳定值，不随频率的改变而改变，证明了破碎后细颗粒含量的有界性[21]，可以为振动压实级配演化过程提供参考。

图7 不同频率下粒径RMC变化Fig.7 Variations of particle RMC with different frequencies

3.2 颗粒破碎特性

为进一步描述振动压实作用下粗颗粒破碎特性，在振动频率为25 Hz，名义振幅为0.3 mm，振动时间4 min工况下进行压实，并通过染色追踪的方法对粗颗粒进行标记，待压实后统计各粒径颗粒破碎质量，并根据GUYON[22]提出的分类方法，对颗粒破碎的类型进行划分为破裂、破碎和研磨3种形式，如图8所示。

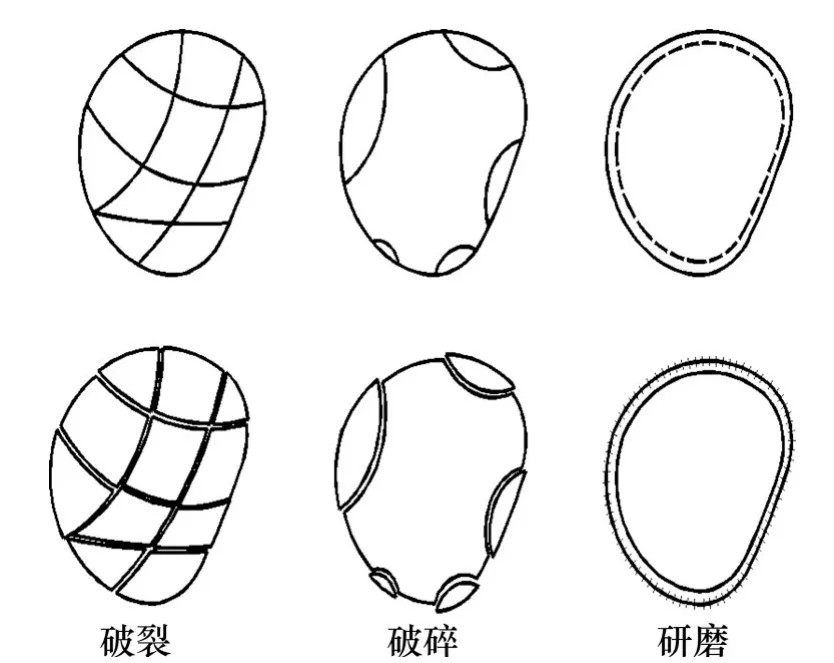
图8 颗粒破碎类型示意图Fig.8 Sketch map of particles breakage types

图9(a)和图9(b)分别展现出成型后试样的横剖面及纵剖面，可以看出染色粗颗粒间并未直接接触，而是由细颗粒填充于粗颗粒之间，即悬浮密实型组构[23]，因此未形成以粗颗粒骨架的力链，导致粗颗粒间应力集中现象减少，难以发生粗颗粒破裂，主要以研磨、破碎类型为主。

图9 振动压实后试样剖面图Fig.9 Specimens profile after vibration compaction

为了定量描述振动压实前后试样的颗粒破碎程度，采用BOBBY等[24]提出的相对破碎率Br作为度量指标展开分析，计算公式如式(8)～(10)所示。

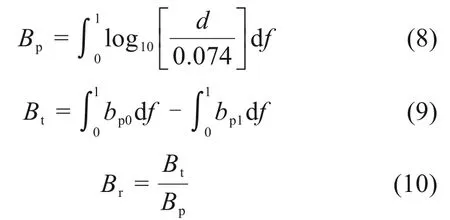
式中：d是颗粒粒径；bp是粒径d对应的潜在破碎可能性，bp0和bpf分别为压实前后土体的bp值；Bp为破碎势，Bt为破碎量；df为bp对应粒径的筛分通过率；Br为土体的相对破碎率。

求得试样在不同频率下振动压实后的破碎率Br并绘制破碎率与频率、干密度关系图如图10所示，可以看出破碎率随频率的增大而增大，与频率和干密度间关系呈现出相同的变化趋势，并在振动频率为最优频率区间时破碎率出现最大值，说明破碎率与填料的密实程度有关，即干密度越大，颗粒破碎率越大，但破碎量的增加往往会改变填料的物理力学性质，所以使用最优振动频率对土体压实时应考虑颗粒破碎对压实性能造成的影响。

图10 频率与破碎率、干密度的关系Fig.10 Relationships between frequency and broken rates

4 结果讨论

现场振动压路机的工作参数除振动频率、名义振幅外还包括碾压速度、碾压遍数；现场实际碾压速度和碾压遍数需根据室内振动次数结果进行确定。同时现场施工时需注意以下事项：

1)填筑路基时，应确保填料粗细颗粒混合均匀，避免出现粗细颗粒集中出现，引起路基压实不均匀[25]。

2)确保现场填料含水率为最优含水率，防止由含水率不足或过多，引起路基欠压实或粗细颗粒发生离析。

3)现场进行压实时，应先进行1～2次静压使压实度达到80%并摊铺平整，防止振动压路机实际振幅过大造成压路机使用寿命减小[26]。

由于室内条件与现场边界条件的不同，室内完全侧限条件下更有利于压实，导致试验结果偏大，现场施工时需适当增加振动次数。

5 结论

1)振动击实频率对干密度的影响可分为3个阶段：10 Hz≤f<15 Hz，缓慢增加；15 Hz≤f<25 Hz，迅速增加；25 Hz≤f<30 Hz，共振，并确定高速铁路B组填料最优振动频率为25～30 Hz。

2)振动压实激振力对干密度的影响同样可以分为3个阶段：0≤PsCL2=110 kPa。

3)振动压实次数对干密度的影响仍然划分为3个阶段：0≤ρ*＜0.6，快速线性增加阶段；0.6≤ρ*＜0.9，非线性增加阶段；0.9≤ρ*<1,缓慢线性增加阶段，此阶段材料达到密实状态。最优振动频率及激振荷载作用下，B组填料合理振动次数n为2 500～5 000次之间。

4)颗粒破碎造成的小于2 mm颗粒的RMC值趋于稳定，证明了颗粒破碎的有界性；颗粒破碎类型以研磨破碎为主，颗粒破碎率随频率的增加而增加，在最优频率区间出现最大值。