一类基于广义比例积分观测器的磁悬浮系统分散输出反馈抗干扰控制
穆静静, 张会远, 兰奇逊*, 李亚杰, 杨玉骞, 徐华锋
(河南城建学院 a. 数理学院; b. 土木与交通工程学院, 河南 平顶山 467036)
磁悬浮列车作为新型轨道交通工具,具有良好的发展前景.电磁悬架作为磁悬浮列车悬架形式之一, 广泛应用于磁悬浮列车.由于任何一种电磁悬架都受系统内部不确定因素和外来干扰的影响, 所以针对磁悬浮系统开展抗干扰控制具有重要的意义和价值.近年来,磁悬浮系统抗干扰控制的研究受到了广泛关注,并取得了一些有意义的成果[1-3].Vo等[4]提出了一种自适应定时干扰观测器和定时控制算法相结合的控制器,并给出了在固定时间收敛的鲁棒控制方法,提高了系统的跟踪精度;李维[5]针对磁悬浮列车系统的非线性特性,在建立系统结构模型的基础上,分别对系统进行基于平衡状态点处的线性控制和反馈线性镇定控制,并利用幂次趋近律和双幂次趋近律的滑模控制算法对系统进行改善;刘武斌等[6]将轨道弹性加入悬浮模型,在使用Hankel范数近似法对模型进行降阶的基础上设计系统的控制算法,解决了轨道弹性引发的系统镇定问题.以上算法均针对磁悬浮系统中的不同控制问题, 采用不同方法提高了闭环系统的鲁棒性能和抗干扰能力.为了快速补偿/抵消干扰的影响[7-10], Yang等[11]通过设计合理的干扰补偿增益,提出一种新的复合控制器来抵消磁悬浮系统输出通道的不匹配干扰,扩展了基于干扰观测器控制方法的适用性;针对磁悬浮系统受负载不确定性和外部干扰的情况下,Li等[12]基于反步法和扩张状态观测器技术,提出一种自适应控制方法;针对磁悬浮列车半转向架结构系统, Chen等[13]利用扩张状态观测器技术,提出分散抗干扰控制方法.本文拟运用广义比例积分状态观测器(generalized proportional integral observer,GPIO)技术[8-9]和输出反馈占优技术[14],实现一类磁悬浮列车半转向架结构系统的分散输出反馈抗干扰控制,以期提高系统的抗干扰能力.
1 问题描述


图1 半转向架结构示意图Fig.1 Structural sketch of semi-bogie

(1)
其中
f1(t,x(t))=-kxksx11-kxcsx12-kzksx21-kzcsx22,f2(t,x(t))=-kzksx11-kzcsx12-kxksx21-kxcsx22,
(2)

|fi(t,x(t))|≤c(|x11|+|x12|+|x21|+|x22|),i=1,2.
(3)
本文的目的是利用系统的输出信息设计分散抗干扰控制器, 使系统输出yi(t)跟踪参考轨迹ri(t).

(4)

2 主要结果
为了实现系统(4)的分散输出反馈抗干扰控制, 假设:

2.1 广义比例积分观测器的设计
(5)
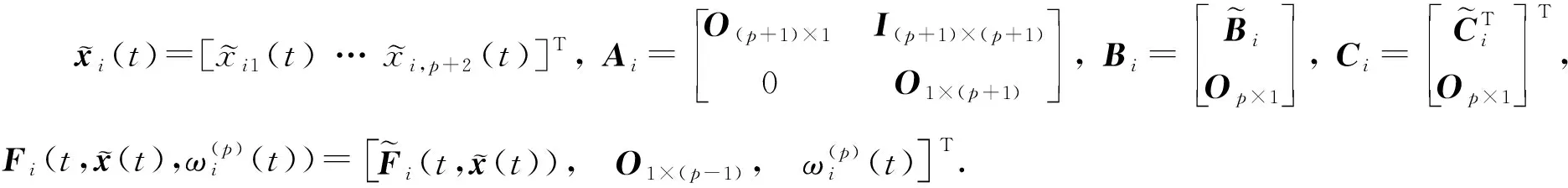
(6)

(7)

2.2 分散输出反馈抗干扰控制器的设计
根据GPIO对系统未测量状态和干扰的估计, 可为系统(6)设计分散输出反馈抗干扰控制器
(8)
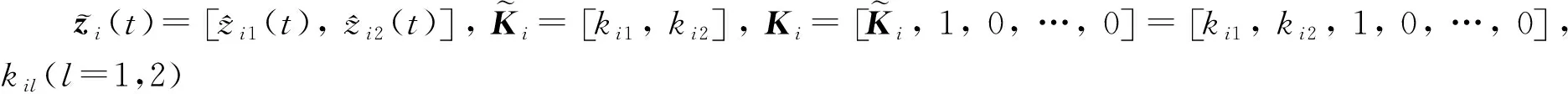
3 闭环系统稳定性分析

(9)
代入式(8), 得闭环系统
(10)



(11)

(12)
故若假设1和假设2成立,则闭环系统(10)的所有状态全局收敛到有界区域B.定理1得证.
推论1对于互联系统(1), 如果假设1和假设2成立, 且当t→∞时,θ→0, 则根据复合控制率(8), 整个闭环系统(10)全局指数稳定.

注1在假设2中,扰动模型ωi(t)设定为带有误差项的p阶泰勒多项式,该模型可以用来描述广泛种类的扰动,例如常值干扰,多项式干扰等.根据设计的广义比例积分观测器,p越大, 获得的估计效果也会越好;当p=1时,广义比例积分观测器将简化为扩张状态观测器.
4 仿真分析
取真空磁导率μ0=4π×10-7N·A-2, 重力加速度g=9.81 m·s-2, 每个电磁铁的有效面积A=0.001 4 m2, 半转向架的质量m=5.2 kg, 半转向架的长度l=0.65 m, 二阶系统的弹性系数ks=0.05, 二阶系统的阻尼因数cs=0.05.


图2 子系统1Fig.2 Subsystem 1

图3 子系统2Fig.3 Subsystem 2

