基于复合干扰观测器的三相逆变器控制方法

黄赛金, 沙 骏, 胥 峥, 杨 波, 王翔宇*

(1. 东南大学a. 自动化学院; b. 复杂工程系统测量与控制教育部重点实验室, 南京 210096;2. 国网江苏省电力有限公司盐城供电分公司, 江苏 盐城 224008; 3. 中国电力科学研究院有限公司, 南京 210003)

随着全球生态环境日益恶化和化石能源枯竭, 开发和利用可再生能源已成为世界主要国家的战略选择．三相逆变器是风力发电、光伏发电等可再生能源并网以及交直流电网互联的重要接口[1], 其可靠稳定运行对电力系统有着重要意义．然而, 在实际应用中三相逆变器系统性能常常受到干扰影响, 例如, 负载投切变化引起的干扰、系统内部参数摄动、输入电压侧的周期性干扰等．为处理上述干扰影响, 提升三相逆变器系统性能, 研究人员已提出多种控制算法, 如比例积分微分(proportional integral derivative, PID)控制、重复控制、滑模控制、自适应控制和模型预测控制等．

PID控制[2]具有易于实现、经济性好等优点, 在三相逆变器实际工业控制中得到广泛应用, 但其控制性能很大程度上取决于控制增益的选取, 依赖工程经验,适应性较差, 且无法精确跟踪周期参考信号; 重复控制[3-5]适用于周期参考信号的跟踪控制, 通过建立周期信号模型并嵌入到控制系统中, 可实现周期信号零稳态误差跟踪, 但其存在控制滞后性, 闭环系统动态性能较差; 滑模控制[6-7]和自适应控制[8-9]对系统参数摄动等干扰具有一定鲁棒性, 但滑模控制存在抖振的缺陷, 而自适应控制一般较为复杂, 计算量大, 难以在实际工程应用中推广; 模型预测控制[10-13]在三相逆变器控制中得到较好应用, 能处理参数受限、控制量耦合等问题, 但缺点在于计算量较大, 成本较高．上述控制方法可从不同角度提升三相逆变器系统性能, 但大多是基于反馈偏差调节的被动抗干扰控制, 对干扰的抑制和处理不够直接、快速．

主动抗干扰控制是根据干扰测量值或估计值在控制器中对干扰进行前馈补偿的控制方法, 能有效弥补上述控制方法的不足, 已得到广泛应用[14-16]．曹文远[1]和Kim[17]等将受负载投切变化影响的负载电流视为系统干扰, 通过设计负载电流观测器估计电流值, 并将其前馈补偿, 从而抑制负载投切变化对系统的影响; Do[8]、Dang[9]、Nguyen[10]等利用干扰观测器处理三相逆变器系统中的负载突变干扰及内部参数摄动; Li等[18]采用扩张状态观测器估计三相逆变器系统中的内部参数摄动, 并进行前馈补偿,以解决参数摄动对系统的影响．在离网运行环境下, 现有三相逆变器抗干扰控制方法大多研究的是限定为常值或慢变类型的负载侧干扰及系统内部参数摄动, 对于输入侧的谐波干扰考虑较少, 而实际工程应用中三相逆变器系统在控制器输出到三相逆变桥输出过程中常会受到谐波干扰影响．为解决上述问题,本文拟设计一种能够同时准确估计负载侧突变干扰和输入侧周期性干扰的复合干扰观测器,并构造基于干扰估计值的前馈补偿项, 与比例微分(proportional derivative, PD)控制器相结合,提出复合控制方法, 抑制干扰影响, 以期改善三相逆变器闭环系统的动态和稳态性能．

1 基础知识与问题描述

1.1 基础知识

记维数为n的零向量0n=[0,…,0]T∈Rn．

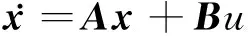
1.2 系统建模与问题描述

在离网运行环境下, 三相逆变器由直流电压源(Vdc), 三相脉宽调制逆变器, 滤波电感(L), 滤波电容(C)和三相负载构成,其系统框图如图1所示．

图1 三相逆变器系统框图Fig.1 Block diagram of a three-phase inverter system

由基尔霍夫电压/电流定律, 三相逆变器系统数学模型为

(1)

(2)

在两相旋转坐标系下, 三相逆变器最常用的控制方法是双闭环比例积分(proportional integral, PI)控制, 但基于反馈偏差调节的PI控制器难以快速抑制干扰对系统的影响, 并且在有输入侧谐波干扰的情况下, 无法实现负载电压的零稳态误差跟踪．为提升闭环系统抗干扰性能及动态和稳态性能, 本文将进一步研究含有负载侧干扰和输入侧周期性干扰的三相逆变器系统(2)的输出电压跟踪问题．

2 控制设计与稳定性分析

2.1 干扰观测器与控制器设计方案

(3)

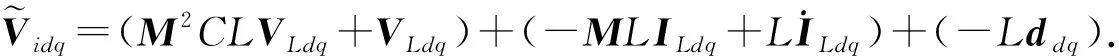
为补偿x2动态中与输出电压VLdq有关的分量, 控制量Vidq分为Vidq-d和Vidq-i两部分, 其中Vidq-d=M2CLVLdq+VLdq,Vidq-i将在后续控制设计中给出．将Vidq代入式(3), 系统模型变换为

(4)

(5)

根据系统模型(5), 复合干扰观测器(composite disturbance observer, CDO)设计为

(6)

基于干扰估计值, 构造前馈项, 并与PD控制器相结合, 复合控制器(PD+CDO)设计为

(7)

其中k1和k2为控制器增益．

在后续仿真对比中和PD反馈控制加干扰观测器(disturbance observer, DO)前馈补偿的复合控制方法(PD+DO)及PID控制方法进行对比．干扰观测器设计为

(8)

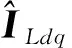
(9)

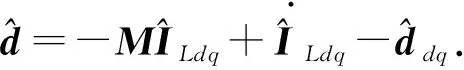
(10)

PID控制器为

(11)

其中kI和kD分别为积分环节和微分环节的控制参数,τ为积分变量．

2.2 闭环系统稳定性分析

闭环控制系统框图如图2所示．首先, 霍尔传感器实时测量电感电流和输出电压, 将测得的三相电感电流和三相输出电压,通过坐标变换至两相旋转坐标系;其次,根据变换后的状态信息(即电感电流和输出电压),采用复合干扰观测器实时估计负载侧突变干扰和输入侧周期性干扰,并结合干扰估计值和状态信息,利用复合控制器计算控制量;最后,将控制量进行坐标变换和空间矢量脉宽调制(space vector pulse width modulation,SVPWM), 生成开关信号, 控制三相逆变桥,实现输出电压的跟踪控制．

图2 闭环控制系统框图Fig.2 Block diagram of the closed loop control system

(12)

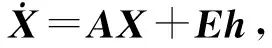
(13)

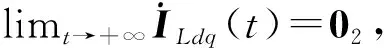
定理1在假设1下, 通过调节观测器增益和控制增益, 复合干扰观测器(6)的观测误差和系统(5)的输出跟踪误差都将渐近收敛到零, 闭环系统渐近稳定．

证明 基于假设1和引理1, 通过调整控制增益和观测器增益, 使A为Hurwitz矩阵, 则误差向量X渐近收敛到06, 即复合干扰观测器(6)的观测误差和系统(5)的输出跟踪误差均渐近收敛到零, 闭环系统渐近稳定．证毕．

3 仿真分析

为验证本文所提PD+CDO控制方法的有效性, 在MATLAB/Simulink平台进行仿真测试, 并与PD+DO复合控制方法及PID控制方法进行对比．系统主要参数如下: 直流电压源Vdc=650 V, 滤波电感L=0.01 H, 滤波电容C=0.001 F, 负载电阻R=100 Ω,d轴输出电压设定值为220 V,q轴输出电压设定值为0 V．仿真过程中, 在0.5 s处输入侧突加100 V、50 Hz的谐波干扰, 同时负载电阻从100 Ω突降至60 Ω．

3种控制器的具体参数如表1所示．通过理论分析, 观测误差系统矩阵的极点-P(P>0)位于左半平面才能使观测器系统稳定; 极点配置越远, 系统收敛速度越快, 但初始阶段系统的超调越大, 且观测器系统矩阵极点越远, 带宽越大, 引入噪声越多．因此, 观测器增益的选取须兼顾收敛速度和噪声, 本文通过调节增益,将四重极点配置于-400处．图3为3种控制方法下三相逆变器系统d-q轴控制输入的仿真对比图．由图3可知, 3种控制方法的控制量幅值在同一水平, 确保了仿真测试的公平性．

表1 控制器参数

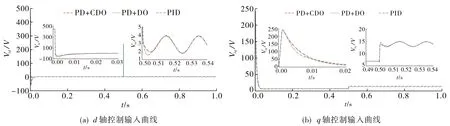
图3 控制输入对比图Fig.3 Control input comparison diagrams

图4和图5分别为3种控制方法下三相逆变器系统d-q轴输出电压和电感电流的响应曲线图．由图4可知, PD+CDO控制方法作用下三相逆变器系统具有更好的输出电压跟踪性能, 启动阶段PD+CDO控制方法作用下系统输出电压超调量更小, 且调节时间更短; 干扰突加处PD+CDO控制方法作用下系统的恢复性能也优于PID和PD+DO控制方法, 且在有输入侧谐波干扰时能实现电压的零稳态误差跟踪．由图5可知, PD+CDO控制方法作用下系统电流响应的动稳态性能更佳, 有谐波干扰时, PD+CDO控制方法作用下电流的稳态性能也显著优于PID和PD+DO控制方法．

图4 输出电压仿真对比图Fig.4 Output voltage simulation comparison diagrams

图5 电感电流仿真对比图Fig.5 Inductance current simulation comparison diagrams

3种控制方法具体的仿真结果如表2所示．其中调节时间指从零时刻到输出电压跟踪误差进入电压稳态值±5%且不再越出的时间; 恢复时间指从干扰施加到输出电压跟踪误差进入电压稳态值±5%且不再越出的时间; 超调量和调节时间为系统启动阶段, 波动量和恢复时间为干扰突加处．由表2可知, 启动阶段PD+CDO控制方法较PD+DO和PID控制方法作用下系统输出电压具有更小的超调量, 且调节时间较短;干扰突加处PD+CDO控制方法的恢复时间和波动量小于PD+DO和PID控制方法,且PD+CDO控制方法作用下系统的总谐波失真(total harmonic distortion,THD)分量更小．综上得出, 本文提出的PD+CDO复合控制方法具有较好的控制性能,能够有效改善三相逆变器系统的抗干扰性能及动态和稳态性能．