汽车发动机弹性齿轮平衡系统动态特性分析

周震宇, 韦源源, 尹 航, 龚俊杰*, 陆永乐, 王 卫

(1. 扬州大学机械工程学院, 江苏 扬州 225127; 2. 扬州保来得科技实业有限公司, 江苏 扬州 225127)

发动机振动是汽车振动和噪声的主要来源之一, 影响汽车运行时的平稳性和舒适性[1]．针对发动机的振动特性及减振措施, 国内外学者进行了深入的研究．Cellek等[2]分析1.4 L四缸奥拓发动机在不同节气门开度和不同转速下垂直轴的振动特性, 发现不同节气门速率下发动机转速的增加均会引起垂直轴振幅的增加; 胡鸿飞[3]通过在发动机前端安装橡胶扭振减振器以降低发动机的扭转振动, 得出双级并联扭振减振器对轴系的减振效果较单级扭振减振器更加明显; Huang[4]对涡喷发动机进行振动测试,将采集到的发动机压气机壳体和涡轮壳体振动信号进行功率谱分析,发现涡喷发动机主转子质量不平衡会引起振动; Jin等[5]运用智能传感器检测农业机械中的发动机振动,指出双层隔振系统能够有效减少发动机振动．四缸发动机平衡系统多选用齿轮传动来传递运动和动力,但在齿轮啮合过程中, 内部激励会产生振动和噪声[6-7]．为了尽量减少振动,使发动机满足高速、低噪声、低振动的要求,本文拟将弹性齿轮运用到汽车四缸发动机平衡系统中,采用弹性齿轮替代金属齿轮作为从动齿轮,分析弹性齿轮平衡系统的固有频率,评价平衡系统运转过程中的减振效果,以期为汽车四缸发动机平衡系统减振技术的发展提供科学依据．

1 发动机弹性齿轮平衡系统模型构建

为满足汽车发动机平衡系统高速转动要求, 须通过柔性环节吸收齿轮的高频振动．弹性齿轮采用橡胶圈作为阻尼环[8], 轮毂与外齿圈分开,橡胶圈粘接在轮毂和外齿圈之间, 具体结构如图1所示．弹性齿轮平衡系统主要由1个驱动齿轮、2个从动齿轮和2个平衡轴组成, 其中驱动齿轮、平衡轴、从动齿轮的外齿圈和轮毂材料选用20CrMnTi, 密度为7 850 kg·m-3, 弹性模量为2.06×105MPa, 泊松比为0.30; 中间减振材料采用氟橡胶, 密度为1 800 kg·m-3, 弹性模量为4.44 MPa, 泊松比为0.48．2个从动齿轮设计为弹性齿轮, 与驱动齿轮接触的弹性齿轮为从动齿轮1, 另一个为从动齿轮2．驱动齿轮和从动齿轮设计参数如表1所示．

表1 齿轮基本参数

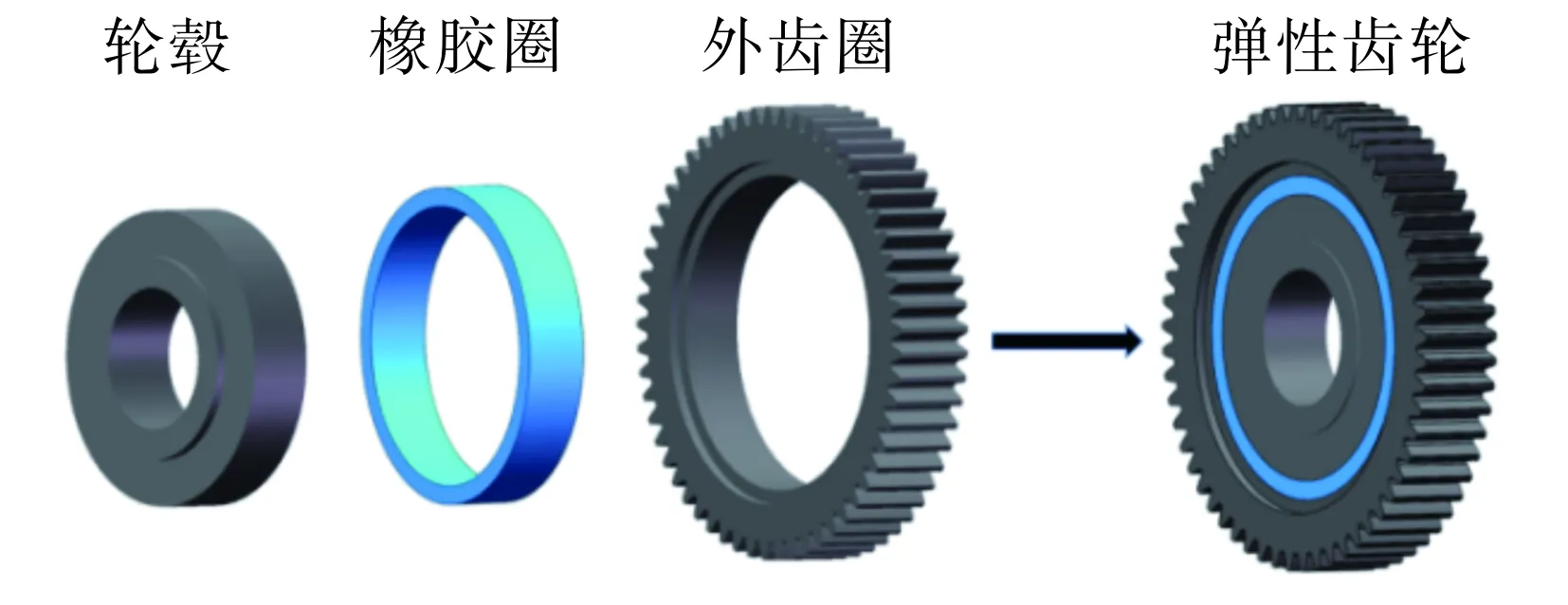
图1 弹性齿轮结构示意图Fig.1 Schematic diagram of elastic gear structure

图2为发动机弹性齿轮平衡系统有限元模型．平衡系统模型划分为257 990个实体单元, 共442 959个节点．齿轮间的运动副接触区域建立Frictional接触, 摩擦系数设置为0.05, 2个弹性齿轮的外齿圈和轮毂与橡胶减振元件采用绑定接触．

图2 弹性齿轮平衡系统有限元模型Fig.2 Finite element model of elastic gear balancing system

2 平衡系统模态分析

在结构振动中, 低阶模态对结构的影响较大, 因此主要考虑低阶模态的固有频率与齿轮副工作频率是否会产生共振[9]．本文对弹性齿轮平衡系统和金属齿轮平衡系统的前六阶模态进行对比分析, 图3为弹性齿轮平衡系统的不同模态振型．由图3可知, 平衡系统振型从一阶模态到四阶模态变形量逐渐增大, 随后又逐渐降低, 其中四阶模态平衡系统变形量最大, 为3.738 mm．

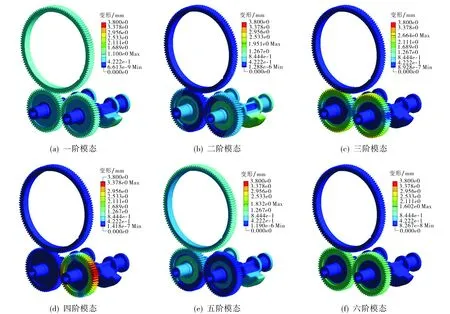
图3 弹性齿轮平衡系统的不同模态振型Fig.3 Different modes of vibration of elastic gear balancing system

表2为弹性齿轮平衡系统和金属齿轮平衡系统的不同模态固有频率和振型．由表2可知,除一阶固有频率相近外, 金属齿轮平衡系统的固有频率均远大于弹性齿轮平衡系统．齿轮啮合频率f=nz/60, 其中n为齿轮转速, r·min-1;z为齿轮齿数．汽车正常行驶过程中, 发动机转速约为1 000～3 500 r·min-1, 齿轮啮合频率约为1 900～6 650 Hz．通过对比发现,弹性齿轮平衡系统前六阶固有频率远小于齿轮啮合频率, 因此, 采用弹性齿轮能够使平衡系统较好地避免运转时齿轮啮合引起的共振．

表2 两种平衡系统不同模态固有频率和振型

3 平衡系统瞬态分析

为了进一步验证弹性齿轮在发动机平衡系统的减振性能, 对平衡系统进行瞬态动力学分析．橡胶是一种超弹性材料[10], 受力过程中具有材料非线性和几何非线性,以及各向同性、不可压缩的超弹性特征,因此在平衡系统动态分析中, 橡胶减振材料采用Mooney-Rivlin[11]五参数模型的自建Rubber材料．氟橡胶Mooney-Rivlin模型的材料系数[12]为C10=-2.11 MPa,C01=3.19 MPa,C20=0.43 MPa,C11=-0.28 MPa,C02=1.43 MPa,D1=0．

3.1 匀加速运动工况

汽车四缸发动机转速可在5 s左右从0 r·min-1加速到3 000 r·min-1．根据发动机运转情况, 从0 s到0.4 s驱动齿轮转速由0 r·min-1到240 r·min-1, 分析发动机平衡系统匀加速工况, 对比弹性齿轮平衡系统和金属齿轮平衡系统的计算结果．图4为弹性齿轮平衡系统和金属齿轮平衡系统的最大应力和最大应变对比结果．由图4可知, 两种平衡系统最大应力随转速增加趋势相同,弹性齿轮平衡系统的变形远大于金属齿轮平衡系统．

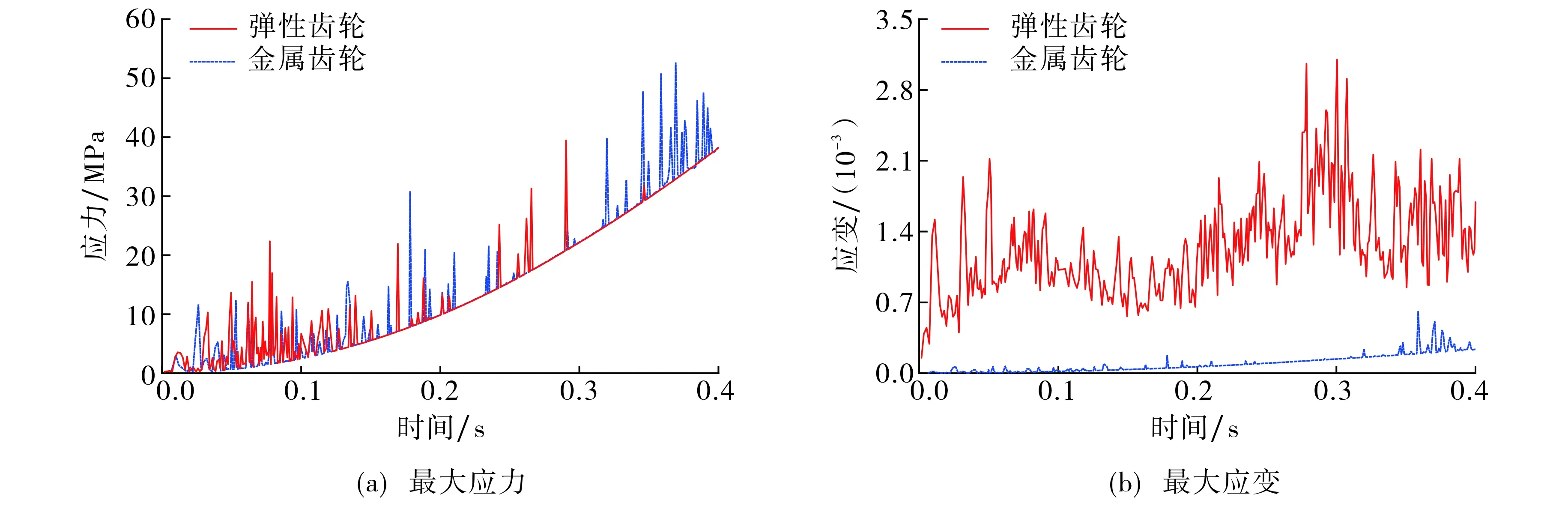
图4 平衡系统最大应力和最大应变对比图Fig.4 Comparison diagram of maximum stress and maximum strain of balance system

平衡系统通过齿轮啮合最终将运动和动力传递给平衡轴, 平衡轴的振动情况能够反映系统的振动效果．提取平衡轴轴心A点加速度变化值, 结果如图5所示．由图5可知, 在转速为0～240 r·min-1的低速运行过程中,弹性齿轮平衡系统A点的加速度远大于金属齿轮平衡系统, 此时弹性齿轮平衡系统运转产生的振动远大于金属齿轮平衡系统．

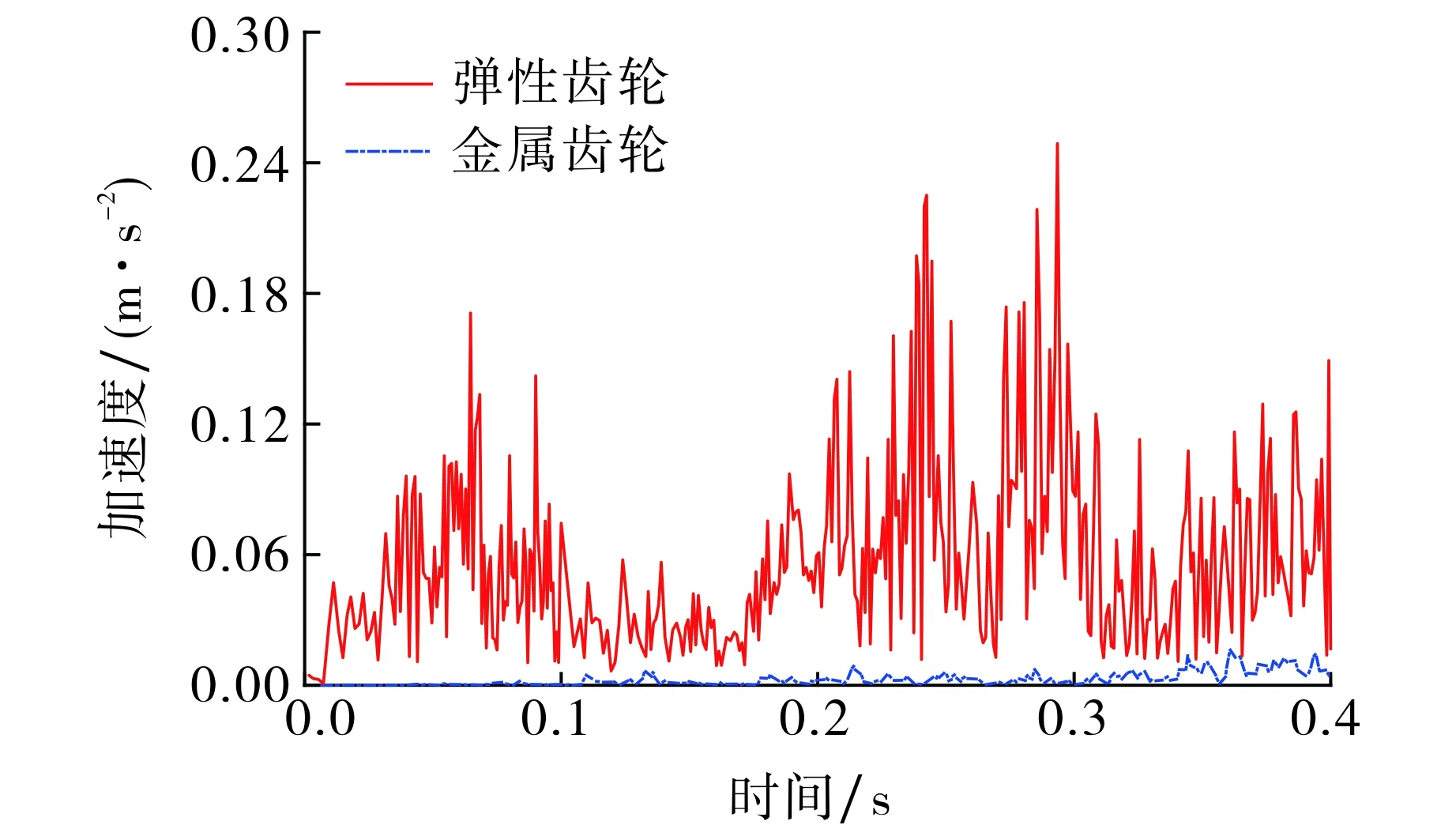
图5 A点处加速度对比图Fig.5 Acceleration contrast map at point A

3.2 匀速运动工况

发动机转速为3 000 r·min-1左右时, 输出扭矩最大, 之后扭矩和转速呈反比, 所以车辆在正常行驶时发动机转速在3 000 r·min-1左右较为合适．为了便于求解平衡系统匀速运动工况, 将动力学分析分为两个阶段．首先是匀加速阶段, 时长为0.02 s, 使驱动齿轮转速由0 r·min-1加速到3 000 r·min-1; 其次是匀速阶段, 从0.02 s到0.04 s, 驱动齿轮转速保持在3 000 r·min-1．

图6为0.02 s到0.04 s匀速运动状态下弹性齿轮平衡系统的应力和应变云图．由图6可知, 弹性齿轮平衡系统最大应力出现在2个弹性齿轮接触面及其附近区域, 最大应力为740.7 MPa, 小于20CrMnTi屈服极限850 MP; 弹性齿轮平衡系统的最大应变出现在弹性齿轮橡胶圈处, 最大应变为0.286 3, 而轮毂和外齿圈部分应变小于0.031 8, 可忽略．图7为橡胶圈应力和应变云图．由图7可知, 橡胶圈作为减振元件, 最大应变出现在主从动齿轮1橡胶圈的外圈上,最大应变为0.286 3, 最大应力为2.719 MPa, 小于橡胶的许用应力18 MPa．

图6 平衡系统应力和应变图Fig.6 Stress and strain diagram of balance system

图7 橡胶圈应力和应变图Fig.7 Stress and strain diagram of rubber ring

对相同工况下金属齿轮平衡系统进行动态分析, 提取0.02 s到0.04 s齿轮匀速啮合状态下平衡轴轴心A点的加速度,结果如图8所示．由于弹性齿轮具有吸收高频振动的效果,在驱动齿轮转速为3 000 r·min-1的工况下, 弹性齿轮平衡系统中平衡轴A点的振动加速度远小于金属齿轮平衡系统中平衡轴的振动加速度, 弹性齿轮在高速转动时具有良好的减振效果．

图8 A点处加速度对比图Fig.8 Acceleration contrast map at point A

4 结论

本文将弹性齿轮运用到四缸发动机平衡系统中,建立了弹性齿轮四缸发动机平衡系统模型, 分析了平衡系统的动态特性．结果表明, 系统高速运转时弹性齿轮能够有效降低传动过程中的振动, 为弹性齿轮在四缸发动机平衡系统中的应用提供了理论依据．