带有输入饱和的化工聚合过程抗干扰跟踪控制

顾 翔, 张晓莉, 周 鹏, 裔 扬

(扬州大学信息工程学院, 江苏 扬州 225127)

在高分子化工领域, 乳液聚合具有多相性和可比较性等特点且能为产品提供更高的通用性, 故多数情况下聚合效果均优于本体聚合和溶液聚合[1]．乳液聚合生成高分子聚合物的过程中, 由于链长不同而导致聚合物性质(如热力学特性、硬度或抗冲击强度等)差异, 所以通过对聚合反应的全过程控制来改变聚合物的粒径分布(particle size distribution, PSD)对于化工聚合物的微观质量控制具有重要意义[2-3]．乳液聚合过程中粒子成核机理的多样性和复杂性使得聚合过程对外部干扰极为敏感, 但已有的研究大多基于反应机理考虑温度或乳化剂种类等对反应的影响, 却未考虑其他种类干扰甚至是饱和现象和干扰同时存在的情况下体系的稳定性问题[4]．

B样条函数因在理论上可逼近任意紧集上的连续函数而被广泛应用于各类函数的逼近与拟合[5-6]．本文拟应用B样条函数将乳液聚合体系中的分布控制问题简化为对一组已知权重的动态跟踪．当被控系统受外部干扰影响时,采用基于干扰观测器的控制 (disturbance observer control, DOBC)算法进行干扰观测及补偿时反应速度快且适应性良好[7-8]．当系统中存在饱和现象时传统的抗干扰控制策略效果较差, 故林宗利[9]和邵立人[10]等采用凸包表示法, 通过引入辅助矩阵将饱和约束完全线性化,从而提高控制效率．本文将对化工乳液聚合的动态过程进行机理建模并引入B样条函数逼近其粒径分布, 在DOBC算法中引入凸包表示法处理执行器饱和限制, 研究同时存在不确定性干扰和执行器饱和情况下系统的抗干扰分布控制．

1 模型建立

考虑一种半连续VAc(醋酸乙烯酯)/BuA(丙烯酸丁酯)乳液聚合体系．根据其动力学方程[11], 建立物质平衡方程:

(1)

进一步地, 聚合物的粒径分布函数为

(2)

式中Zentry(r),Zdesorption(r),Ztermination(r)分别表示低聚自由基进入、解离和终止的频率．选定一组B样条基函数ξi(r)(i=1,2,…,n), 重新表示目标粒径分布函数为

(3)

式中vi(t)表示与基函数对应的权值．由于基函数是预先确定的, 所以控制的目标可转换为对一组权系数vi(t)的动态跟踪问题．建立控制输入和权系数向量间的动态模型:

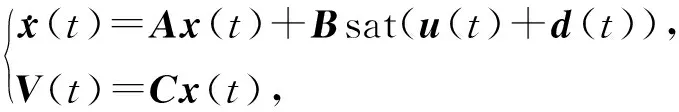
(4)

式中x(t)为状态向量;A,B,C为系统矩阵; sat(·)表示饱和约束;u(t)为系统输入;d(t)为外部干扰, 可由模型

(5)

来描述, 其中w(t)为干扰系统的中间状态,M,N为与干扰类型有关的系数．为了能够获得良好的跟踪性能,扩张系统描述如下:

(6)

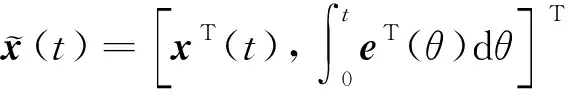
2 控制器设计

为了对干扰d(t)进行估计和补偿, 现构造如下干扰观测器:

(7)

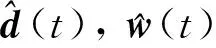
对饱和约束设计凸包进行线性化处理:

(8)

(9)

结合式(7) (9)易得

(10)

3 性能分析

(11)

(12)

(13)

(14)

4 仿真分析

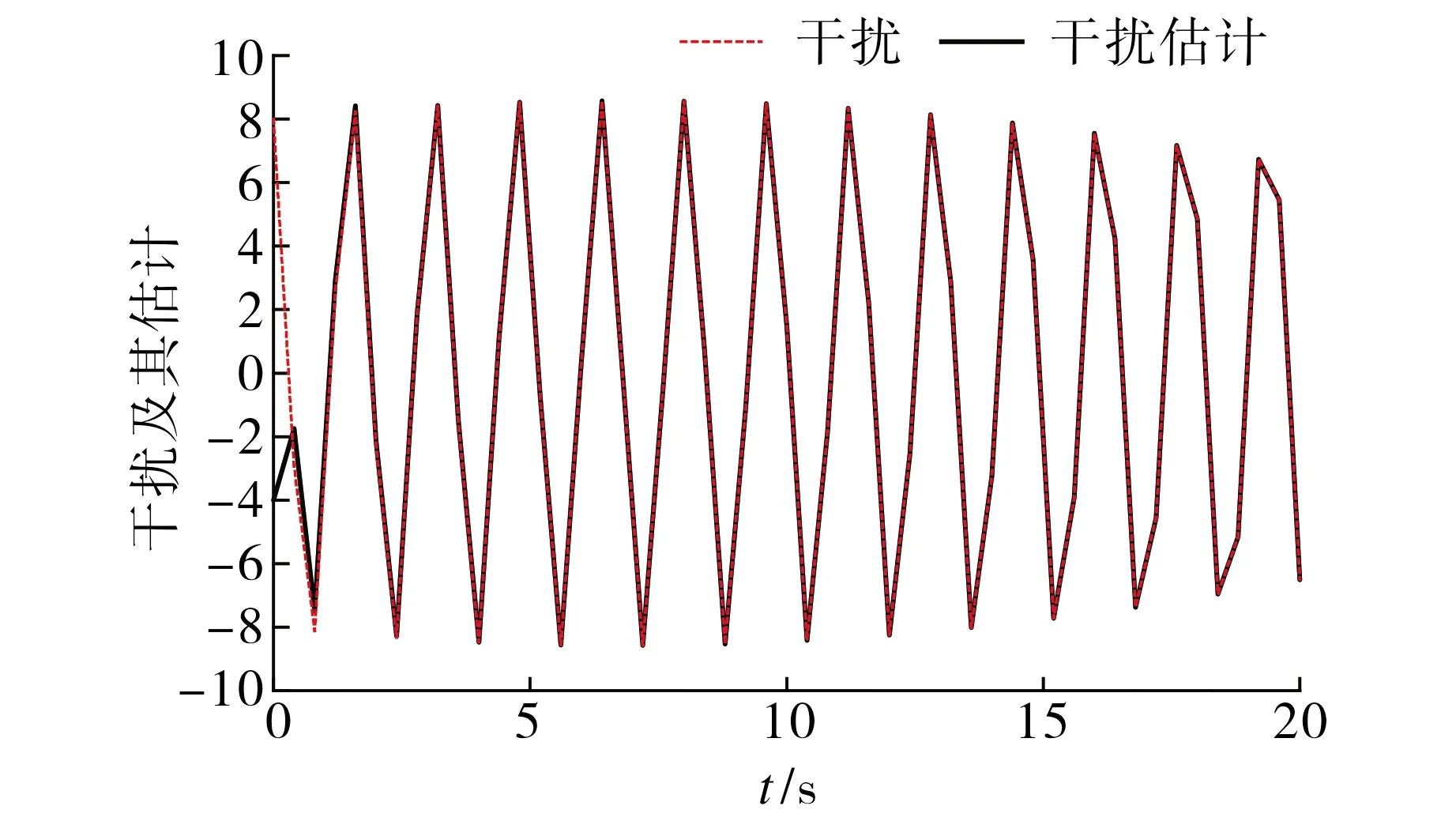
图1 干扰及其估计值Fig.1 Disturbance and its estimation

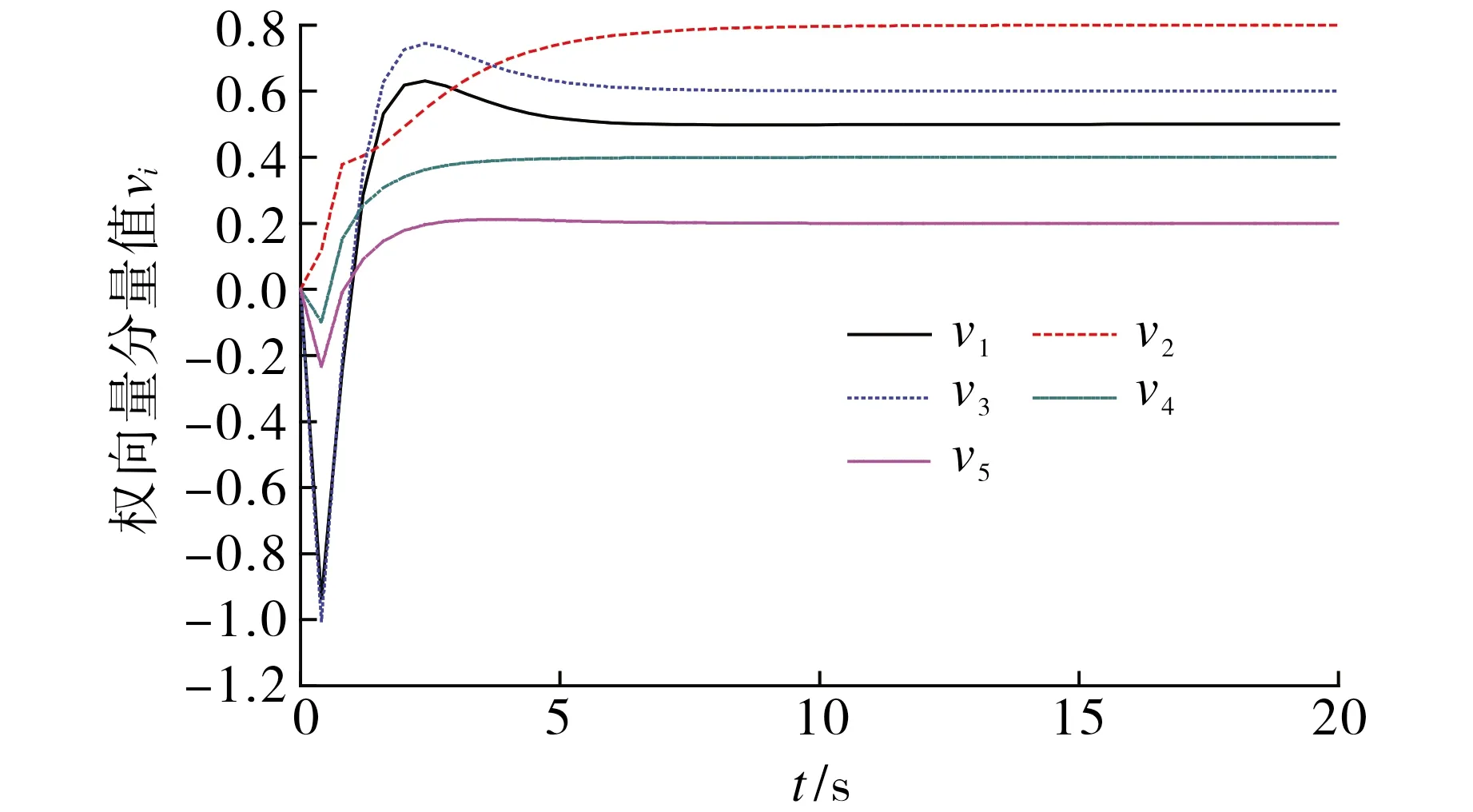
图2 动态跟踪性能Fig.2 Dynamic tracking performance

图3为采用DOBC算法前后输出PSD的3维分布图．由图3可见,在采用DOBC算法后,输出聚合物的粒径具有良好的分布特性．

图3 采用DOBC算法前后输出PSD的3维图Fig.3 3-D plot of output PDFs with and without DOB control method

5 结论

本文针对半连续VAc(醋酸乙烯酯)/BuA(丙烯酸丁酯)乳液聚合体系进行建模,利用B样条函数对系统的粒径分布函数进行逼近,将控制问题转化为对一组已知权系数的跟踪问题．基于Lyapunov分析方法,在考虑存在干扰和输入饱和的情况下,向系统中引入干扰观测器和凸包表示设计复合控制器,保证系统的稳定性和良好动态跟踪性能,并获得良好的PSD分布．