Toeplitz矩阵填充的加速临近梯度截断算法
闫喜红, 姬路鑫, 王 政
(太原师范学院a. 数学系; b. 管理系, 太原 030619)
矩阵填充问题因在机器学习[1]、图像恢复[2]、计算机视觉[3]等领域被广泛应用而备受关注.Candès等[4]认为, 通过求解优化问题
min ‖X‖*, s.t.Xij=Mij,∀(i,j)∈Ω
(1)

Toeplitz矩阵作为一种特殊的重要矩阵, 在图像处理, 信号处理等方面起到了至关重要的作用[9].针对Toeplitz矩阵的特殊结构, 王川龙等人利用Toeplitz矩阵的快速奇异值分解算法, 提出了Toeplitz矩阵填充的均值算法[10]和改进的増广Lagrange乘子算法[11]等, 这些算法都能使每步的迭代矩阵保持Toeplitz矩阵结构.众所周知,加速技巧可以使算法在运算效率方面进一步提高[8].本文拟利用文献[8]中给出的截断技术,针对Toeplitz矩阵提出了两种加速临近梯度截断算法.
1 预备知识
定义11个n×n的Toeplitz矩阵定义为
定义2(奇异值分解(singular value decomposition,SVD)) 对于秩为r的矩阵X∈Rn1×n2, 则必存在正交矩阵U∈Rn1×r和V∈Rn2×r, 使得X=UFrVT, 其中Fr=diag(σ1,…,σr), 式中σ1≥σ2≥…≥σr≥0.
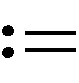
注文献[8]中提出的APG算法是针对求解一般矩阵填充问题的算法; 而本文要解决的填充问题是针对Toeplitz矩阵的, 故本文提到的APG算法是在文献[8]的APG算法步3中将矩阵X进行Toeplitz化后再进行迭代.

2 加速临近梯度截断算法
众所周知, 对未运用任何加速技巧的APG算法, 迭代矩阵Xk的奇异值通常会分离成2个簇, 且第一个簇的均值比第二个簇的均值要大得多, 从而可以把第一个簇类中奇异值的数量看作模型(1)低秩最优解秩的一个估计数.此外, 第二个簇中较小的正奇异值(在μ/τ附近)可能导致数据M中存在噪声, 故可将第二个簇中奇异值抛弃而不影响算法的收敛性.因此, 本文提出第一种算法(A), 步骤如图1所示.
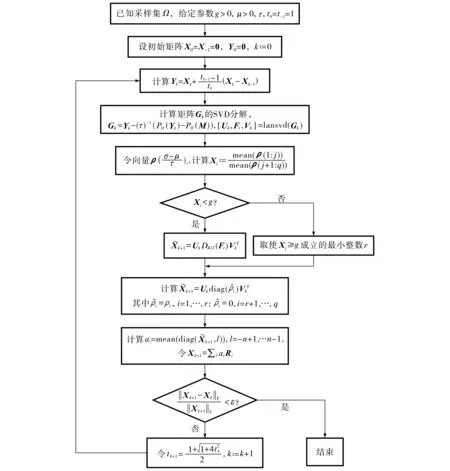
图1 加速临近梯度截断算法(A)流程图Fig.1 Accelerated proximal gradient truncation algorithm(A)
算法A每次迭代过程中出现的截断都会消耗时间, 故为了减少计算量, 提高算法的运算效率, 提出了改进的算法(B).算法B的流程如图2所示.

图2 w步加速临近梯度截断算法(B)流程图Fig.2 w-Steps accelerated proximal gradient truncation algorithm(B)
3 收敛性分析
利用模型(1)的罚函数可以将Toeplitz矩阵填充问题转化为无约束优化问题:
(2)

假设1假设模型(2)存在最优解, 记为X*.
假设2对于矩阵Xk+1, 如下不等式成立:

证明 根据文献[8]中引理2.1, 有F(Xk+1)≤Q(PL(Yk+1),Yk+1)≤Q(Xk+1,Yk+1), 从而
F(X)-F(Xk+1)≥F(X)-Q(Xk+1,Yk+1).
(3)
又因f,g是凸的, 则f(Xk)≥f(Yk+1)+〈Xk-Yk+1,f(Yk+1)〉,g(Xk)≥g(Xk+1)+〈Xk-Xk+1,μ∂‖Xk+1‖*〉.将上述不等式相加, 得F(Xk)≥f(Yk+1)+〈Xk-Yk+1,f(Yk+1)〉+μ‖Xk+1‖*+〈Xk-Xk+1,μ∂‖Xk+1‖*〉, 代入式(3), 由假设2得F(X)-F(Xk+1)≥F(X)-Q(Xk+1,Yk+1)≥〈Xk-Yk+1,f(Yk+1)〉+〈Xk-Xk+1,μ∂‖Xk+1‖*〉-〈Xk+1-Yk+1,f(Yk+1)〉-证毕.
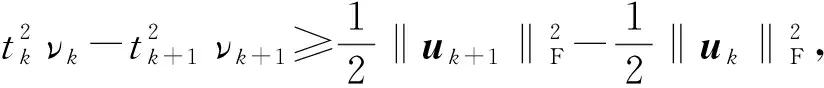
证明 由引理1得
(4)
(5)

引理3[12]令{ak,bk}为正实数序列, 满足ak-ak+1≥bk+1-bk, 并且对任意的k≥1, 有a1+b1≤c,c>0.那么, 对于任意的k≥1都有ak≤c.
引理4[12]正序列{tk}由算法A或B产生, 对于t1=1, 满足任意的k≥1时, 有tk≥(k+1)/2.

4 数值实验
通过数值实验比较本文算法与APG算法.计算机的CPU为Intel Core i3-4030U, 内存4 GB, 操作系统为Windows 8, 所有代码由MATLAB编写.实验中, Toeplitz矩阵的维数n分别取100,200,300,400,500,1 000,2 000,3 000; 采样率p分别取 0.3,0.4,0.5;Y表示最优解;m表示迭代次数; 运行时间t,s;r(X)=5; 参数Lf=1,ε=10-4.不同算法的数值实验结果对比见表1.从表1可以看出, 本文提出的2种新算法的迭代次数均比APG算法少, 运行时间也较短, 且新算法的精度比APG算法更优.
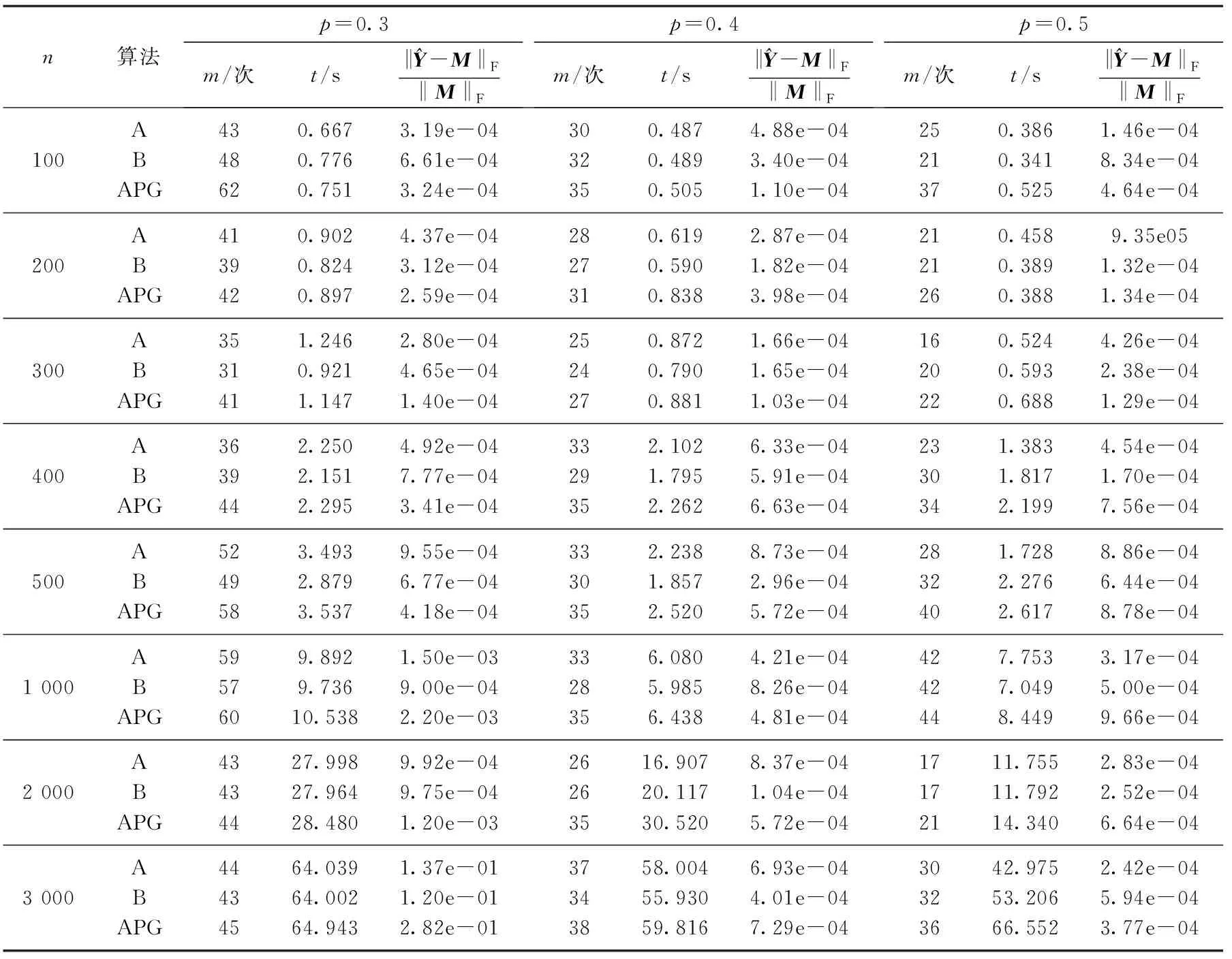
表1 不同算法的数值实验结果对比

