基于误分类代价的粗糙模糊集近似集

2021-11-08 03:05杨洁，袁利，罗天

重庆邮电大学学报(自然科学版) 2021年5期

杨洁，袁利，罗天

(1.遵义师范学院物理与电子科学学院，贵州遵义 563002；2.云南大学软件学院，昆明 650091)

0 引言

作为粒计算[1-2]的工具之一，粗糙集[3]是一种利用当前信息粒来处理不确定性信息的有效模型，即采用上、下近似集对不确定性目标概念进行近似描述。作为粗糙集的扩展模型，粗糙模糊集[4]是一种有效处理目标概念为模糊集时的粒计算模型，通过定义上、下近似集来刻画一个模糊目标的概念，从而进行知识获取，更具有普遍性。当前，有许多关于粗糙模糊集方面的研究，大致分为3个方面：理论研究，扩展模型和应用。其中，Rehman[5]提出了基于向上可加一致性的广义多粒度模糊粗糙集模型，构造了一种新的多属性决策方法。Xue[6]提出了基于多粒度支持直觉模糊粗糙集的三支决策模型，设计了一个决策规则提取算法。Li[7]提出了基于粗糙模糊理论的双定量多粒化决策模型，研究了包含相对定量信息和绝对定量信息的决策规则。Yang[8]借鉴Vague集中支持度和反对度的思想,构建了多粒度邻域粗糙模糊集的不确定性度量方法。

近年来，Zhang[9-10]分别从模糊距离和相似度的角度出发，提出了经典粗糙集近似集的相关理论，通过利用已知信息粒直接对目标概念进行近似描述，从而构建粗糙集的近似表示，一方面，证明了该近似集比上、下近似具有更高的近似度；另一方面，证明了0.5-近似集在一定约束条件下是最优近似集，即阈值为0.5时最优。在粗糙集近似集的基础上，Zhang进一步研究了粗糙模糊集近似集[12]和vague集的近似集[13]的相关理论，并将近似集理论应用到属性约简[14-15]、图像分割[16]、粒度优化[17]等领域上。虽然当前粗糙集近似集理论方面具有一定的研究成果，但是，基于隶属度的近似集可能存在对象误分的情形[18]，而从决策风险的角度出发，通常希望划分结果带来的误分类代价尽可能小，此时基于相似性的近似集模型不再适用于代价敏感的应用场景。现实应用中，误分类代价是一种决策代价，分析误分类代价在一定程度上有助于提高决策质量。从三支决策[19]的角度来说，边界域中的等价类在作为近似集时会产生误分类代价，如何使得构建的近似集的误分类代价最小是值得研究的问题。再者，在分层递阶的多粒度知识空间中，随着知识空间的细化，边界域中对象可能会发生重新分类，使得边界域中用于表示近似集的等价类发生变化，从而导致每个知识空间上近似集的误分类代价也会随之发生变化。

从多粒度的角度来说，在不同粒层上对同一个问题进行近似处理的结果可能具有相近的意义，但是这些近似处理的误分类代价不尽相同。因此，针对以上问题，本文从误分类代价的角度，提出了粗糙模糊集近似表示模型，以保证得到的近似集对应的误分类代价在当前粒度下最小，并在此基础上进一步研究了多粒度知识空间中误分类代价的变化规律。

1 相关定义

在介绍粗糙模糊集的不确定性度量之前，我们先回顾一些基本概念。

定义1(粗糙集)[3]设一个信息系统S=(U,C∪D,V,f),R⊆C，X⊆U, 那么X的上、下近似集分别定义为

(1)

(2)

(1)—(2)式中，[E]R代表由等价关系U/R诱导的等价类, 即U/R={[E]R}={E1,E2,…,El}。

(3)

(4)

(5)

定义2(粗糙模糊集)[4]设一个信息系统S=(U,C∪D,V,f),R⊆C，X是一个在U上的模糊集, 那么X的上、下近似集可以定义为一对模糊集，其隶属度分别定义为

(6)

(7)

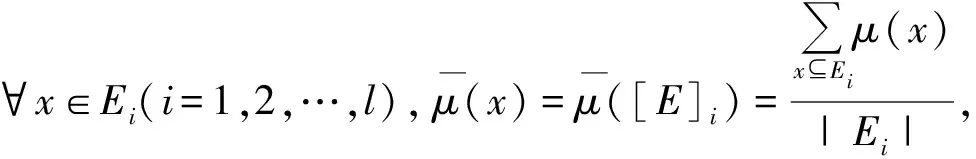
传统的粗糙集没有利用现有的知识粒近似刻画边界不确定的目标概念，为了利用已有信息粒构建目标概念的近似刻画，文献[10]从隶属度的角度给出了粗糙模糊集的近似表示方法，如定义4。

定义4(基于隶属度的粗糙模糊集近似集)[10]

假设S=(U,C∪D,V,f)是一个信息系统，R⊆C，X是U上的一个模糊集。U/R={E1,E2,…,El}为U上的一个知识空间，则在U/R上对X的α近似表示可定义为

0<α≤1

(8)

例1给出了一个关于选取优秀教师的信息系统(见表1)。R1，R2和R3分别代表3个评估指标(科研、获奖、教学)，为了方便说明，假设它们的属性值为离散值，D是决策属性。

表1 有关选取优秀教师的信息系统

2 基于误分类代价的粗糙模糊集近似表示

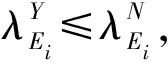
定义5假设R={R1,R2,R3}是一个信息系统，R⊆C，X是U上的一个模糊集。U/R={E1,E2,…,El}为U上的一个知识空间。λ11表示当对象x属于目标概念X时将x作为近似表示时所产生的损失函数，λ12表示当对象x不属于目标概念X时将x作为近似表示时所产生的损失函数，λ21表示当对象x属于目标概念X时将x不作为近似表示时所产生的损失函数。λ22表示当对象x不属于目标概念X时将x不作为近似表示时所产生的损失函数。则U/R中等价类被用于近似描述X的误分类代价表示为

(9)

U/R中等价类不被用于近似描述X的误分类代价表示为

(10)

(11)

定义6设一个信息系统S=(U,C∪D,V,f)，阈值α、β(0≤β≤α≤1)，R⊆C，X是U上的一个模糊集，U/R={E1,E2,…,El}为U上的一个近似空间，那么X的上、下近似集分别定义为

(12)

(13)

论域U通常被划分为正域、负域和边界域，分别定义为

(14)

(15)

(16)

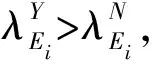
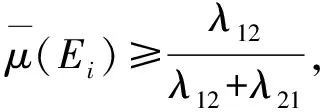
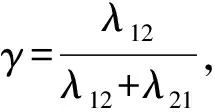
本文进一步提出了基于误分类代价的粗糙模糊集近似集，如定义7所示。

定义7(基于误分类代价的粗糙模糊集近似集)

假设S=(U,C∪D,V,f)是一个信息系统，R⊆C，X是U上的一个模糊集，U/R={E1,E2,…,El}为U上的一个近似空间。令

(17)

(17)式中，Ei∈U/R。称R(X)为基于误分类代价的粗糙模糊集近似集。

图1 基于误分类代价的近似集(折线所围部分)

(18)

定理1设一个信息系统S=(U,C∪D,V,f)，R⊆C，X是U上的一个模糊集，U/R={E1,E2,…,El}为U上的一个近似空间，则以下性质成立

(19)

(20)

(19)—(20)式中，Ei∈U/R(i=1,2,…,l)。

由定理1可知，BNDI(X)域中等价类用于作为近似集时的误分类代价总是小于或等于不作为近似集时的误分类代价，BNDII(X)域中等价类不用于作为近似集时的误分类代价总是小于或等于作为近似集时的误分类代价。

证明：由定义6可知

(21)

(22)

(23)

由于BND(X)=BNDI(X)∪BNDII(X)，可得

(24)

(25)

因此，由定理1可得

定理3设一个信息系统S=(U,C∪D,V,f)，R⊆C，X是U上的一个模糊集，U/R={E1,E2,…,El}为U上的一个近似空间，当λ1=λ2时，R(X)=R0.5(X)。

证明：由条件可知，当λ1=λ2时，由定义6可得γ=0.5。

由定理3可知，当λ1=λ2时，基于误分类代价的粗糙模糊集近似集R(X)将退化为R0.5(X)。

3 多粒度知识空间下的粗糙模糊集近似表示

随着信息的不断完善，知识空间不断细化，边界域中对象可能会发生重新分类，导致边界域中用于表示近似集的等价类发生变化。本节将分析多粒度知识空间中粗糙近似集模型误分类代价的变化规律。

定理4设一个信息系统S=(U,C∪D,V,f)，R1⊆R2⊆C，X是U上的一个模糊集，则DC(R1(X))≥DC(R2(X))。

证明：假设U/R1={E1,E2,…,El}和U/R2={F1,F2,…,Fm}是U上的2个知识空间。由于R1⊆R2，故U/R2⪯U/R1。为了简单化，假设仅有一个信息粒E1(E1∈U/Ri)细分为2个更细的信息粒F1，F2(F1,F2∈U/R2)(其他复杂情形均可转化为这种情形，这里不再重复)，则E1=F1∪F2,E2=F3,E3=F4,…,El=Fm(m=l+1)，即U/R2={F1,F2,E2,E3,…,El}。

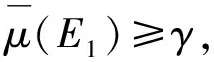
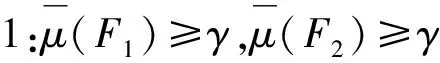
由情形1可知，F1⊆R(X)，F2⊆R(X)。如图2a为BNDI(X)中等价类发生细分的一种情形，可知

图2 近似集模型的BNDI(X)中等价类发生细分情形

(26)

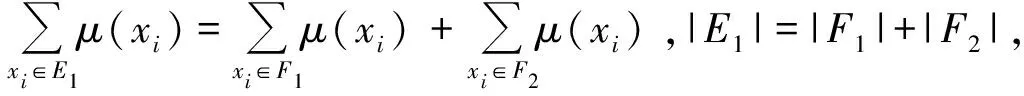
由情形2可得：F1⊆R(X)，F2⊄R(X)。图2b为BNDI(X)中等价类发生细分的一种情形，可知

ΔDCR1-R2=DC(R1(X))-DC(R2(X))=

(27)

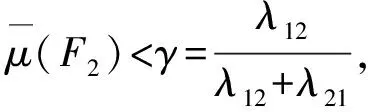
由情形1可知，F1⊆R(X)，F2⊄R(X)，图3a为BNDII(X)中等价类发生细分的一种情形，可得

图3 近似集模型的BNDII(X)中等价类发生细分情形

(28)

由情形2可得，F1⊄R(X)，F2⊄R(X)，图3b为BNDII(X)中等价类发生细分的一种情形，可知

(29)

综上所述，无论为哪种情形，DC(R1(X))≥DC(R2(X))都成立，因此，定理4成立。定理4表明知识空间近似模糊概念的误分类代价随着粒度的细化呈单调递减，这个结果符合人的认知习惯。

为了简化，本文仅以BNDI(X)为例，分析它对应的误分类代价的变化规律。

定理5设一个信息系统S=(U,C∪D,V,f)，R1⊆R2⊆…⊆RM⊆C，X是U上的一个模糊集，仅有BNDI(X)中的信息粒通过ΔR=R1-R2发生细分，则DCR1(BNDI(X))≤DCR2(BNDI(X))。

证明：假设U/R1={E1,E2,…,El}和U/R2={F1,F2,…,Fm}是U上的2个知识空间。由于R1⊆R2，故U/R2⪯U/R1。为了简单化，假设仅有一个信息粒E1(E1∈U/Ri)细分为2个更细的信息粒F1，F2(U/R2⪯U/R1)(其他复杂情形均可转化为这种情形，这里不再重复)，则E1=F1∪F2,E2=F3，E3=F4,…,El=Fm(m=l+1)，即U/R2={F1,F2,E2,E3,…,El}。