基于三支决策的高斯混合聚类研究
万仁霞,王大庆,苗夺谦
(1.北方民族大学 数学与信息科学学院,银川 750021;2.同济大学 计算机科学与技术系,上海 201804)
0 引 言
高斯混合模型(Gaussian mixture model,GMM)[1]是由k个单高斯模型组合而成的模型,这k个子模型是混合模型的隐变量。高斯混合模型可以看作是K-means模型的一个优化,是一种生成式模型,理论上可以拟合出任意形状的数据分布。何明等[1]针对数据统计分布的随机性和复杂性,从统计聚类的角度出发,采用高斯混合模型来描述整个数据的概率密度函数,从而提出了一种基于高斯混合模型的粗糙聚类分析方法。Najar等[2]对流行的有限高斯混合模型进行了深入的研究,分别评估了4个著名的基于高斯混合模型的数据聚类性能。Wang等[3]为了解决当数据稀缺时,基于高斯混合模型的传统聚类算法不再有效的问题,提出了一种基于高斯混合模型的传输聚类算法,利用源域中的数据信息对目标域中的数据进行聚类。王宏伟等[4]从概率统计方法出发,提出了一种基于高斯混合模型聚类与递推最小二乘算法的非均匀采样系统的多模型建模方法。陶志勇等[5]针对高斯混合聚类算法对初始值敏感且容易陷入局部极小值的问题,利用密度峰值算法全局搜索能力强的优势,对高斯混合聚类算法的初始聚类中心进行优化,提出了一种融合密度峰值的高斯混合聚类算法,解决了其对初始聚类中心依赖的问题。此外,高斯混合聚类能够较好地捕获属性之间的相关性和依赖性,对异常值有较强的可识别性[6]。
高斯混合聚类依据概率分配聚类成员,因此,相较于经典的K-means聚类具有更灵活的类簇形状。风险及代价在指导人们做出某项决策时具有重要的意义,而现有的高斯混合聚类算法及其改进并没有考虑到聚类错误的风险及代价。
三支决策(three-way decisions,3WD)理论是由加拿大学者Yao在2010年提出的一种朴素的“三分而治”和“化繁为简”的决策理论[7]。该理论从应用的角度对粗糙集的核心概念正域、负域和边界域给出了合理的语义解释[8-9]。由于三支决策符合人类思维和认知特点,且能较好地处理实际决策过程中出现的不确定性问题,它一经提出便得到国内外学者的广泛关注,刘盾等[10]从三支决策3个历史发展阶段出发,通过粗糙集和粒计算2个研究视角对三支决策的发展踪迹和演化过程进行介绍;于洪等[11]从类内紧凑性和考虑近邻类间分离性角度出发,定义了分离性指数、聚类结果评估有效性指数,并提出了一种基于K-means的自动三支决策聚类算法,为处理具有不确定信息的基于K-means算法框架的聚类数目自动确定的难题提供了一种新的解决思路。
三支决策理论倾向于关注分类错误带来的风险代价,是具有代价敏感性数据分析的有效工具[12]。三支决策理论中损失函数的确定需要先验信息和专家知识,存在一定的主观能动性,与高斯混合聚类算法的客观性某种程度上形成了互补。本文将三支决策思想融入高斯混合聚类算法中,提出一种基于三支决策的高斯混合聚类算法。
1 相关理论
1.1 高斯混合聚类模型
高斯混合模型是对高斯模型的扩展,同时也是多个高斯分布函数的线性组合[13]。高斯混合模型假设所有的样本数据均服从混合高斯分布,即对样本数据集的概率密度函数进行估计,所估计的模型就是高斯模型的线性组合,每个高斯分布均为一个簇[6]。
高斯混合聚类利用高斯分布概率模型来进行聚类,假设x为n维样本空间M中的随机向量,若其服从高斯分布,则概率密度函数[14]可以表示为
(1)
(1)式中:μ是n维均值向量;Σ是n×n维协方差矩阵。可以看出,该函数由μ和Σ唯一确定,因此,可以将函数表示为p(x|μ,Σ)。

(2)
高斯混合聚类模型中,首先根据先验分布α1,α2,…,αk选择高斯混合成分,αi为选择第i个高斯混合成分的概率,然后根据被选择的高斯混合成分的概率密度函数进行采样,从而生成样本。若数据集D={x1,x2,…,xn}由上述高斯混合过程生成,则令随机变量zj∈{1,2,…,k}表示生成样本xj的高斯混合成分。显然,zj的先验概率P(zj=i)=αi。根据贝叶斯定理,zj的后验分布为
(3)

(4)
对于模型的求解,主要在于求解参数Θ={(αi,μi,Σi)|i=1,2,…,k}。根据给定样本集D,可以采用最大化对数似然的方法,计算公式为
(5)
为使(5)式最大化,常用的求解方法是利用EM算法[15]进行迭代优化,在迭代过程中不断更新参数αi,μi和Σi,直至满足算法迭代终止条件。参数更新公式为
(6)
(7)
(8)
1.2 三支决策
三支决策的研究主要基于决策粗糙集,整个论域被划分成3个部分,即正域(positive region,POS)、负域(negative region,NEG)和边界域(boundary region,BND),分别代表着接受、拒绝和不承诺3种决策结果。决策粗糙集模型理论(decision-theoretic rough sets,DTRS),是由姚一豫等在1990年提出[16-18]。它将概率粗糙集和最小风险贝叶斯决策结合起来,通过计算各类分类决策风险损失值,对POS、NEG和BND进行划分。
文献[19]中对三支决策给出了具体解释:假设有2种状态的集合Ω={X,X},X和X是互补关系的2种状态,即对象属于X或者属于X。由于分类结果有3个域,给定决策集A=(P,B,N),其中P,B,N分别表示将对象划分到正域、负域、边界域的决策行为。由于采取不同决策行为会产生不同的损失,λPP,λBP,λNP分别代表当x属于X时,x被划分到正域、负域、边界域的损失;λPN,λBN,λNN则分别代表当x不属于X时,x被划分到正域、负域、边界域的损失。表1为对应的决策损失矩阵。

表1 3种决策的损失代价矩阵
根据Bayes决策过程的推导,通过引入参数α,β可得到基于决策粗糙集的三支决策规则:
若P(X|[x]R)≥α,则x∈POS(X);
若β 若P(X|[x]R)≤β,则x∈NEG(X)。 其中, (9) (10) 设讨论的对象集合为U={x1,x2,…,xi,…,xN},聚类结果为CS={C1,C2,…,Ci,…,Ck}。其中,x={x1,x2,…,xd,…,xD},k表示类的个数,D表示对象属性个数,xd表示对象x在第d维属性上的值。论域U中任意一个元素必须存在于至少一个类中。 三支聚类结果中一个类C被表示为互不相交的3部分,即CL,CM和CR,又称为L域、M域和R域。L域中的对象确定属于这个类;M域中的对象可能属于这个类也可能不属于这个类;R域中的对象确定不属于这个类。显然,CR=U-(CL∪CM)。类簇C为一个二元组,即C=(CL,CM)。 引入参数α,β且0<β<α<1,三支聚类决策规则如下[20]: 若P(Ci|xj)≥α,则xj∈POS(Ci); 若β 若P(Ci|xj)≤β,则xj∈NEG(Ci)。 三支聚类结果则表示如下: CS={(C1L,C1M),(C2L,C2M),…, (CiL,CiM),…,(CkL,CkM)} 且满足如下性质: i)CL≠∅; ii)∪(CiL,CiM)=U,i=1,2,…,k。 性质i)要求CL不能为空,即为了保证聚类有实际意义,每个类中至少要有一个对象;性质ii)保证了集合U中每个对象至少被划分到一个类中。 算法的主要思想是:将三支决策理论与高斯混合聚类算法相结合得到的一种聚类方法。聚类结果中任意类簇都是由核心域和边界域组成,核心域中的样本比较密集而边界域中的样本相对而言比较稀疏。 算法主要分为2个阶段:①通过高斯混合聚类算法计算每个数据对象由各混合成分生成的后验概率;②以计算出的后验概率为评价函数,进行三支聚类。 输入:样本集D={x1,x2,…,xn},聚类簇数k,最大迭代次数Iter,EM算法收敛阈值ε,损失代价λPP,λBP,λNP,λPN,λBN,λNN。 输出:簇划分结果 CS={(C1L,C1M),(C2L,C2M),…, (CiL,CiM),…,(CkL,CkM)} Step1初始化高斯混合分布模型参数,Θ={(αi,μi,Σi)|1≤i≤k},并根据(9)式、(10)式计算得到α,β的值。 Step2EM算法估计模型参数,计算后验概率。 算法迭代: forj=1,2,…,ndo end for fori=1,2,…,kdo 根据EM算法,更新参数,即 协方差向量: end for fori=1,2,…,kdo 对于每一类Ci,任取xj∈Ci, end for 三支高斯混合聚类(T-GMM)算法主要利用三支决策思想具有代价敏感性的优势,将后验概率作为评价函数进行三支决策划分,通过三支决策划分边界域,以便对边界域对象进行更深一步的分析与决策,避免直接做出属于某一类或不属于某一类的决策所需承担的风险,采取了比一般高斯混合聚类算法更加谨慎的态度,以减小误判风险及代价。 1)实验使用UCI数据库中的8组标准数据集进行验证,具体信息如表2。 表2 实验使用的UCI数据集 2)实验环境为Python 3.7。工作站环境为Windows 10,为Intel(R)core(TM)i5-4200U CPU;4 GByte安装内存;编码语言使用的IDE环境为Anaconda Spyder。 实验结果根据聚类算法评价指标(davies bouldin index, DBI)[21]、轮廓系数[22]进行评价。 1)DBI定义为 (11) (11)式中:ci表示第i类中的所有样本元素到聚类中心wi的平均距离;‖wi-wj‖2表示类i与类j之间的欧式距离;k表示聚类数。DBI评价一个聚类结果的好坏的依据是:要求类内元素相似度高,类间元素相似度低。DBI计算任意两类的类内平均距离之和除以两聚类中心距离求出最大值,DBI越小,意味着类内距离越小,同时类间距离越大,聚类结果质量越高。 2)单个样本xi的轮廓系数Si定义为 (12) (12)式中:ai表示样本xi与同类中其他所有样本的平均距离;ai称为类内相异度,ai越小说明该样本属于该类的可能性越大。(12)式中bi=min{D(xi-cj)},D(xi-cj)表示样本xi到类ci所有样本的平均距离,bi称为类间相异度,bi越大说明该样本属于其他类的可能性越小。也就意味着,轮廓系数值越大,聚类效果越好。 针对部分实验数据集属性个数较大,本文采取PCA方法[23-24]降维之后再进行聚类。在本实验过程中设定λPP=0,λNN=0,λNP=18,λPN=8,λBP=9,λBN=4。根据公式(9)、(10)计算得到阈值参数为β=0.308,α=0.615,EM算法最大迭代次数Iter设为100,收敛阈值ε设为0.001。 图1、图2、图3分别为Vehicle数据集的散点图、GMM聚类和T-GMM聚类的实验效果图,图4、图5、图6分别为Iris数据集的散点图,GMM聚类和T-GMM聚类的实验效果图,图7、图8、图9分别为Ionosphere数据集的散点图,GMM聚类和T-GMM聚类的实验效果图。 图1 Vehicle数据散点图 图2 GMM聚类结果 图4 Iris数据散点图 图5 GMM聚类结果 图7 Ionosphere数据散点 图8 GMM聚类结果 图3、图6、图9中,Co(i)表示类别i的核心域,Fr(i)表示类别i的边界域,图中倒三角代表每一类的聚类中心。 图3 T-GMM聚类结果 图6 T-GMM聚类结果 图9 T-GMM聚类结果 从图3、图6、图9的运行结果图的情况可以得出,在各数据集中清楚地找到了类与类之间的重叠部分,并且把重叠部分的对象划分到了类的边缘域中。通过上述在标准数据集的对比实验结果可以看出,本文提出的T-GMM算法不仅确保了聚类效果,且对于边缘点进行了甄别,根据对象属于各个类的最大概率,对类中对象做进一步区分,从而得出更加丰富的信息,便于后面部分对聚类结果作出进一步分析。 为了进一步测试算法性能,将本文提出的T-GMM与GMM聚类以及K-means聚类算法进行比较试验。基于表2所示数据集上的实验结果,各个算法的DBI和轮廓系数S的评价结果如表3。 表3 各算法的评价指标对比 从表3中可以看出,T-GMM在Vehicle,Iris,Sonar,Vote,Breast,Wpbc等数据集上,对比比较算法均表现出具有更小的DBI值和更大轮廓系数S值,表明T-GMM在这些数据集上有优于GMM,K-means的聚类效果;在Ionosphere数据集的实验结果对比中,可以明显的看出,在DBI评价指标方面T-GMM具有最小值,表明T-GMM得到的类间最大相似度的均值是最低的,具有最好的聚类效果,而在评价指标S方面K-means算法的值最低,这是由于Ionosphere数据集的样本较为分散,而T-GMM主要处理的是边界域,由于边界的重叠性,导致轮廓系数值提高不明显。 图10—图13分别为Sym数据集的散点图,GMM聚类、T-GMM聚类和K-means聚类的实验效果图。图10中,sym数据集包含3个不同形态的数据簇,这一特殊性使得T-GMM,GMM的DBI值和廓系数S值均不如K-means算法。为进一步分析各算法在sym数据集的聚类性能,同时,考虑到数据集本身并不完全为凸形数据簇,而经典的密度聚类方法DBSCAN算法[25]可以处理不同大小或形状的簇,故本文将DBSCAN算法一并作为对比算法进行比较实验。图14为sym数据集在DBSCAN算法下的聚类结果图。 图10 Sym数据集散点图 从图13可以看出,K-means聚类结果准确率不高,其聚类准确率仅为78%,这是因为K-means算法更适用于球形类簇数据集的聚类,对于非球形数据集和不同大小的簇的聚类存在一定的不足。从图14可以明显看出,DBSCAN将原本3个类的数据集聚类成为了2个类簇算法的聚类准确率为仅有71.43%。T-GMM和GMM均能有效识别出3个类簇,由此可见,T-GMM算法对于非球形数据集上的聚类具有很好的聚类性能。 图11 GMM聚类结果 图13 K-means聚类结果 图14 DBSCAN(eps=0.3, MinPts=6)的聚类结果 总体来看,在各个标准数据集上,本文提出的T-GMM聚类算法的聚类效果普遍更好,聚类划分也更加准确。 本文将三支决策思想融入高斯混合聚类算法中,提出一种基于三支决策的高斯混合聚类模型。模型利用高斯混合模型计算得到每个数据对象属于各个类簇的后验概率,以此作为三支决策的评价函数,进行三支聚类,从而确定聚类结果中的正域、负域和边界域。三支决策思想的引入,旨在进一步提高算法的聚类有效性。实验结果表明,对比同类算法,三支高斯混合聚类算法不仅继承了原有算法的优越性能,同时可以得到更好的聚类效果,并且对非球形数据簇的聚类具有良好的性能。1.3 三支聚类[11]
2 基于三支决策的高斯混合聚类
2.1 算法思想
2.2 三支高斯混合聚类






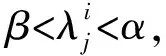

3 实验与结果分析
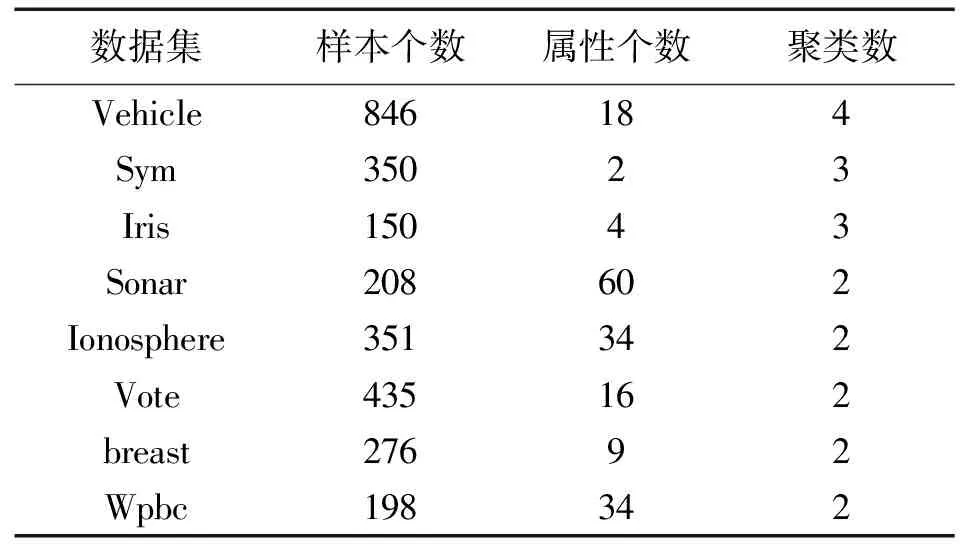
3.1 实验数据与实验环境
3.2 实验评价指标
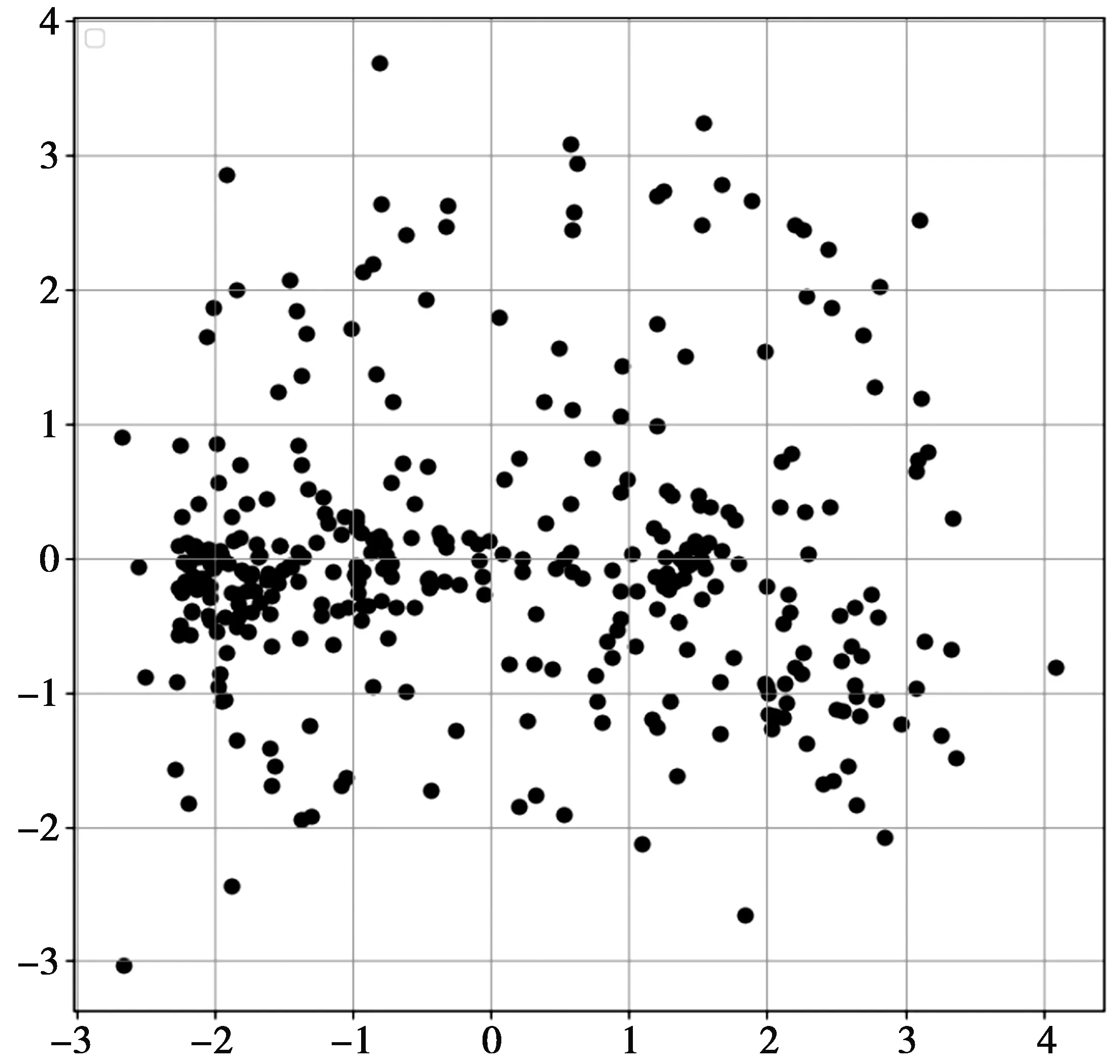
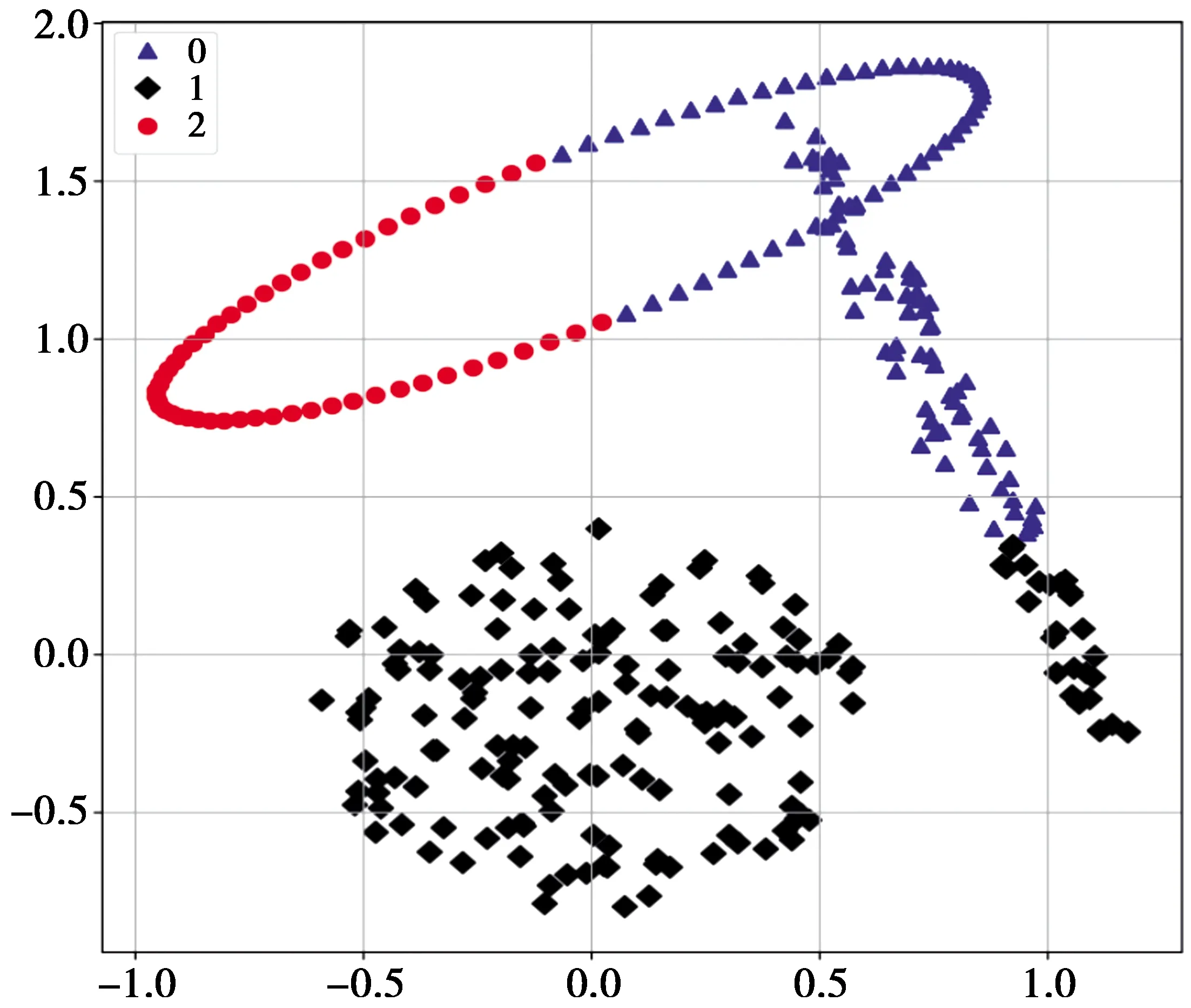
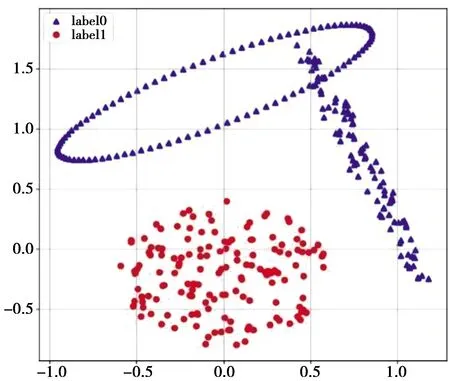
3.3 实验结果分析











4 结束语

