以“运”助“算”，提升学生运算能力

刘凤

[摘 要]运算能力可以进一步拆分为“运”的能力和“算”的能力。其中，“运”的能力侧重于意识领域，指向的是思想、策略，属于高阶思维活动;“算”的能力侧重于技能领域，其指向的是实践，属于具体的操作范式。教学中，教师不但要关注学生“算”的能力的提升，更要注重学生“运”的能力的发展，把“运”与“算”有机结合，使“运”贯穿于“算”的全过程，促进学生运算能力的提升。

[关键词]运算;算理;算法

[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068（2021）29-0084-02

计算教学贯穿小学数学的全过程，因此，培养学生的计算能力是小学数学教学的重要任务之一。计算的基本要求是正确、迅速、合理和灵活，而在实际教学中，有些计算题并不是学生不会做，而是由于注意力不够集中抄错题，以及计算粗心不进行验算所形成的。那么如何提高学生的计算能力呢？笔者就从以下三个方面来谈谈自己的一些体会。

一、运意识之道，求算法之简

思想决定行动，学生“算”的过程实际上是“运”的过程的外化。教学中，运意识之道主要体现在三个方面。一是要培养学生的简算意识。简算是一项重要的运算技能，其中蕴含着丰富的智力，培养学生的简算意识，不但能够提高学生灵活计算的能力，还能提升学生数学思维的深度和广度。然而，在实际教学中，部分学生的简算意识不强，如果题目没有明确要求简算，学生往往会按一般方法进行计算，这就制约了其思维灵活性和敏捷性的发展。二是要培养学生的依据意识。计算要“讲道理”，计算中的每一步都是有“理”可寻的，学生要时刻关注自己的算法是否有依据，有什么依据，只有这样才能避免掉入“盲目简算”的陷阱。三是要培养学生的反思意识。 弗赖登塔尔指出，反思是数学思维活动的核心和动力。教师及时引导学生对计算过程进行回顾和反思，并利用问题：“计算得对吗？计算得巧吗？”引导学生思考，能使学生对多种算法进行比较，在对比和反思中求得最简算法。

【片段1】

师：请同学们计算25×44，可尝试用多种方法计算，看谁的方法更巧妙。

生1：我是列竖式计算的，25×44=1100。

生2：我将数字进行拆分，25×44=25×（40+4）=25×40+25×4=1000+100=1100。这种方法很简便，口算就能得出结果了。

师：你能说一说你的计算依据吗？

生2：我依据的是乘法分配律。

生3：我也将数字进行了拆分，25×44=25×4×11=100×11=1100。

师：你的计算依据是什么呢？

生3：把44拆分为11×4，通过25×4=100实现简便运算。

生4：我是这样计算的，25×44=（25×4）×（44÷4）=100×11=1100，我依據的是积的变化规律。

生5：我是这样计算的，25×44=25×40×4=1000×4=4000。

师：生5的算法对吗？

生（齐）：不对。25×44表示44个25相加，而25×40×4表示160个25相加。

生5：我只顾“凑整”了，应该把44拆分成（40+4）。

师：同学们喜欢哪种算法？

生6：我更喜欢生2的算法，这样口算就能得出结果。

生7：生3的算法也很简便。

生8：我认为生4的算法更巧妙。

……

教学中，首先，教师引导学生打开思路，用多样化的方法算出结果，唤醒了学生的简算意识;其次，教师指导学生讲出计算过程中的依据，加深了学生对算法合理性的认识，使学生的计算“有律可依”，强化了学生的依据意识;最后，教师引导学生对各种算法进行评价和反思，使学生在自我反思中深化认知，探寻到了解决问题的最佳方法。

二、运规则之道，正算法之理

运算是讲规则的。整体而言，运算规则基本可以分为两个部分，即运算法则和运算定律。在运规则之道环节，教师可以从两个方面入手。一是注重法则，让运算“有法可依”，避免运算过程中的主观化和随意化。在运算教学中，教师要引导学生严格按照运算法则进行运算，使学生养成遵守运算法则的运算习惯，确保计算过程的规范性。二是厘清定律，让运算“有律可寻”，避免运算错误。运算定律和运算性质可以打破既定的运算顺序，是实现简便运算的重要途径。无论是运算定律还是运算性质，都是一种模块化的知识，是人们对运算规律的归纳和总结。教学中，教师要引导学生厘清运算定律，防止学生混淆运算定律，导致运算定律的“误用”和“错用”，同时，教师要引导学生适时运用运算定律，实现运算定律的“当用即用”，最大限度地实现计算的简便化。

【片段2】

师：请同学们计算100-63.8+36.2。

生1：100-63.8+36.2=100-100=0。

生2：这样计算不对，应该按照从左至右的顺序计算，100-63.8+36.2=36.2+36.2=72.4。

师：加法和减法属于同级运算，应该按照从左至右的运算法则进行计算，不能单纯为了“凑整”而随意改变运算顺序。请同学们计算8×1.25÷8×1.25。

生3：8×1.25÷8×1.25=10÷10=1。

师：生3这样计算对吗？

生（齐）：不对。

教学中，教师为学生呈现了富有学习价值的素材，引导学生在运算过程中要严格按照运算法则，使学生意识到忽视运算法则就会导致运算结果错误，由此引起学生对运算法则的重视。

【片段3】

师：请同学们计算45×25+25×75。

生1：45×25+25×75=（45+25）×（25+75）=70×100=7000。

生2：45×25+25×75=25×（45+75）=25×120=3000。

师：谁的计算是正确的？他们都运用了“乘法分配律”吗？

生3：生1的计算是错误的，生2的计算是正确的。生2正确运用了乘法分配律，因为原式表示45个25加上75个25，而25×（45+75）也表示45个25加上75个25。

师：请同学们计算176×18+823×18+18。

生4：176×18+823×18+18=3168+14814+18=18000。

生5：我可以用乘法分配律进行简算，176×18+823×18+18=18×（176+823+1）=18×1000=18000。

师：同学们比较一下，哪种方法更简便？

生（齐）：生5的算法更简便。

师：我们在计算时要根据数据特点，巧妙运用运算定律，实现简便运算。

教学中，教师引导学生体验巧用运算定律实现简算，提升了学生运用运算定律和运算性质的意识，避免在计算中发生“当简算时不简算”的现象。通过引导学生对比不同算法，使学生意识到运算定律的“正确使用”和“当用即用”在计算过程中带来的便利。

三、运策略之道，释算法之义

在运算教学中，采用多样化的策略，向学生解释算法的含义，使学生明白其中的算理，可以有效促进学生对算法的理解，提升运算能力。运策略之道可以从两个方面入手。一是创设生动的情境，把抽象算法与生动活泼的生活情景联系起来，不但可以促进学生对算法的理解，还能够赋予数学运算的应用价值。二是充分利用几何直观，通过数形结合实现学生对算法的深度理解，使算法变得鲜活生动。

【片段4】

明星小学四（7）班学生参加植树活动，他们一共分成了7个植树小组，每个植树小组种植5棵树，每棵树需要浇2桶水，那么，他们一共需要浇多少桶水？

生1：我先算出树的棵数，然后再算需要多少桶水，列式为（7×5）×2=70（桶）。

生2：我先算出每个小组需要浇多少桶水，然后再算一共需要浇多少桶水，列式为7×（5×2）=70（桶）。

师：思路不同，算出的结果却是相同的。我们把这两个式子用等号连起来是（7×5）×2=7×（5×2）。同学们还可以再举几个这样的等式吗？

生3：（3×4）×5=3×（4×5）。

生4：（10×4）×3=10×（4×3）。

师：这样的等式我们可以用字母表示为（a×b）×c=a×（b×c）。

教学中，教师把乘法结合律与解决生活中的问题融合起来，通过对乘法结合律的模型建构，促进学生对知识的理解。

【片段5】

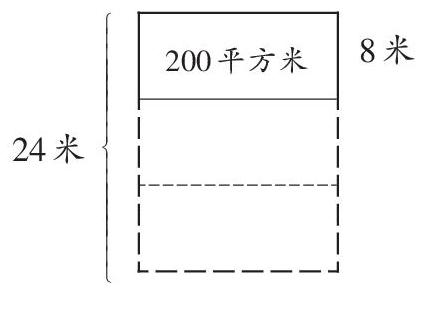
一块长方形绿地，宽是8米，面积是200平方米，如果长不变，宽增加到24米，那么，扩建后的长方形绿地的面积是多少平方米？

生1：可以先求出长方形绿地的長，再计算扩建后的绿地面积，列式为200÷8×24=600（平方米）。

生2：可以用画图的办法解决，根据积的变化规律“一个因数乘（或除以）一个数（0除外），另一个因数不变，积也乘（或除以）这一个数”，8变成24，实际上是乘3，因此，积也乘3，列式为200×（24÷8）=600（平方米）。

教学中，教师引导学生把几何直观和抽象算法相结合，通过画图的方式学生更加深刻地理解了“积的变化规律”的本质。通过对比学生的两种算法，更能促进学生对知识的理解。

综上所述，不少教师非常看重学生“算”的能力，殊不知学生“运”的能力决定了“算”的层次和水平。只有学生“运”的能力强，学生才能“算”得对，“算”得快，“算”得巧。因此，教师在运算教学中，要注重提升学生“运”的能力，以“运”助“算”，从而不断提升运算技能，发展数学思维。

（责编 覃小慧）