三“试”三“生”显图像

潘智

[摘 要]正比例图像是学生必须在小学六年级掌握的，且与初中数学相衔接的知识点。部分教师对这个内容的教学仅仅停留在让学生知道“正比例图像是一条直线”即可。文章透过一次优质课评比试教的准备过程，发现学生对图像理解的误区，并通过分析错误原因，让学生完成对正比例图像由“线段”到“射线”，再到“直线”的认知纠正，从静止走向运动，从离散走向连续，从运算走向关联。

[关键词]正比例图像;统计图;直线

[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068（2021）29-0020-03

区级优质课评比进入第二轮——课堂教学比赛，课题是小学阶段最后学习的“正比例图像”。通过对教材的初步分析，笔者确定了本课的教学目标：让学生初步认识正比例图像，能画出相应的图像，能借助正比例图像解决简单的实际问题。

一、描生图像，事与愿违

在简单准备之后，开始了第一次试教。笔者先出示教材例1的数据，让学生回忆判断“路程”和“时间”成正比例关系;再呈现方格图，并介绍横轴和纵轴;接着和学生一起描点、连点，向学生讲解正比例图像是一条直线;最后根据图像判断汽车2.5小时行驶多少千米，行驶440千米需要多少小时。整个教学过程一气呵成，课堂气氛融洽，学生回答准确无误。学生独立尝试“练一练”时，笔者发现大部分学生绘制的正比例图像都有问题：有的学生画成了一条线段（如图1），有的学生将每两个点分别相连（如图2），有的学生画成了条形统计图（如图3）。为什么学生到了独立绘制图像时却不得要领呢？课后，笔者选取10位学生进行了一一调查。

原来学生中有用画统计图的方法去画正比例图像的，这充分说明，通过一节课的学习，学生并没有掌握正比例图像的本质，反而混淆了正比例图像与统计图的知识。

二、衍生枝节，归因反省

时间紧迫，笔者针对问题加以调整，隔天就进行了第二次试教。教学例1时，笔者仍然先让学生回忆判断两个量成正比例关系、呈现方格图、介绍横轴和纵轴，接着让学生描点。此时，笔者没有急于让学生将描出的点连成线，而是启发学生继续思考：如果汽车行驶9小时，行驶了多少千米？你觉得可以用图4中的哪个点来表示呢？

生1：应该不是C点和D点，不管时间和路程成不成正比例，路程都会随着时间的增加而增加，所以路程不会仍是560千米或比560千米少。

生2：1小时行驶80千米，9小时比7小时多2小时，就多了两个80千米，560+80×2=720（千米），是A点。

生3：我也同意A点，因为用B点的640除以9，除不尽，和前面的点不成直线。

通过对四个点的选择和交流辨析，学生已经将注意力由画图转移到关注两个量之间的关系上，而这也是理解正比例图像的关键所在。

师：如果汽车行驶10小时、11小时，能找到对应的点吗？假设继续行驶下去，这样的点会有多少个？

生（齐）：无数个……

师：请动手将这些点用线连起来，完成正比例图像。

这次画图只用了1分钟，然而展示反馈的结果仍不尽人意：绝大部分学生只是将几个点连成一条线段，只有少数学生将所画的线的一端进行了延长，但没有人将线延长到坐标原点。为了完成试教流程，笔者只得直接指出问题，让学生修改图像后，便匆匆进入巩固练习环节。

练习：小玲用计算机打字的数量和所用的时间如下表。

（1）小玲打字的数量和所用的时间成正比例关系吗？为什么？

（2）先在下图中描出打字数量和时间所对应的点，再按顺序连一连。

学生解第（1）小题时很顺利，可是在第（2）小题的绘图中，有三分之一的学生将正比例图像变样了（如图5）。

怎么会出现图像拐弯的情况呢？笔者改编练习时，特意将“时间10分钟、数量500个”去掉，其本意是让学生在绘图后体会“前后两点之间还有无数个点”的情况，但学生却将第12分钟的点直接画在了第10分钟上。笔者陷入了沉思：学生明明说出会有无数个点，为什么还是只绘制了正比例图像的局部？最令人不解的是，居然没有学生想到正比例图像可以向“0”方向延伸！

带着这些疑惑，笔者再次与学生、教师交流，思路逐渐被打开，对学生出错原因有了新的认识。首先，学生的这些错误绝不是偶然发生的，它真实地反映出学生理解正比例图像时所遇到的困难。正比例图像本质是一种关系，而学生仍停留在对数量理解的基础上。其次，在学生眼中，正比例图像依然只有单个的点，线只是连接两点的辅助，并没有“连续”“无数”的体验。这些关键概念的理解对于尚处于形象思维向抽象思维过渡阶段的小学生来说，难度不言而喻。

三、重生本质，深入浅出

第三次试教开始了，笔者先播放一则广告，通过对其中相关量的描述，将学生的注意力集中于“关系”上。课前给小组分发不同的情境数据表格，有的两个量成正比例关系，有的两个量不成正比例，并组织学生开展研学活动：（1）判断表中两个量是否成正比例？为什么？（2）说说方格图中横轴和纵轴所表示的含义;（3）在方格图上分别描出相应的点，再将各点连接起来。

展示汇报时，笔者请学生先将绘制的图进行分类，学生很自然地分成了两类：一类图像不是直的線，两个量不成正比例;另一类是成正比例关系的图像，但是画得基本都不完整。此时，笔者并没有直接指出问题所在，而是追问：“你们觉得正比例图像是怎样的呢？”不出所料，学生异口同声说是一条线段。笔者板书“线段”。

随后，笔者选择“小玲用计算机打字的数量和所用的时间”这组数据，在表格中插入一列空白列，并呈现思考题：如果打字时间是3分钟，打字数量是150个，你能在这条“线段”上找到这个点吗？如果数量不是150个，这个点还会在“线段”上吗？

一阵短暂沉默后，学生准确找到了“线段”上的点，并加以解释。接着，笔者再次在表格中插入一列空白列，这次是在第一组数据之前。

师：这里可能会出现怎样的数据呢？

生1：这条线段可以向两边延伸。

生2：是的，可以有无数个点，不仅线段上有无数个点，两边也有無数个点。

生3：只要符合这个正比例关系的点都会在这条线段上。

师：看来同学们又有了新发现，那么这条线段可以延伸到哪儿呢？

生4：向左可以到0的位置，向右可以无限延长。

（教师出示调整后的表格）

师：现在图像上有需要改动的部分吗？

生5：正比例图像不是线段，应该是一条射线，在这条线上有无数个点，每个点表示的两个量都成正比例关系。

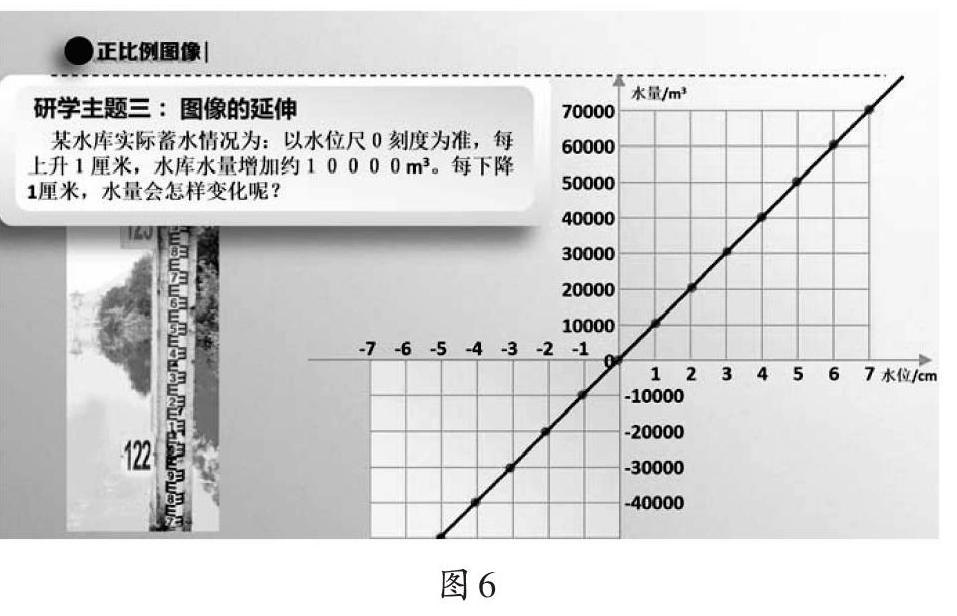
将“线段”替换为“射线”，说明学生的认知被打开，体会到正比例图像的“无数”“延伸”等本质属性。此时，笔者不急于进一步延伸图像，而是通过练习巩固，强化学生对正比例图像的理解，直到最后才呈现有关水库的情境（如图6），引导学生感受水位下降时正比例图像发生的变化，最终将“射线”完善为“直线”。至此，三“试”三“生”终于显露出真正的正比例图像——一条由无数个点组成的直线。

一次赛课、两次反思、三次试教，给笔者带了许多新的思考。

1.线段——知识生长的基础

数学教学应该建立在学生的认知发展水平和已有的经验基础上。在教学“正比例图像”过程中，其所要求的函数思维方式与学生现有的思维水平是有差距的，这是生成图像的主要障碍。如，所有表格呈现的第一组数据均不是0，以学生的认知基础自然认为不从0开始描点。又如，小学阶段所呈现的正比例关系 [yx]=k（一定）中，x的确不能为0。统计图相关知识的负迁移同样是造成错误的重要原因。统计图与正比例图像所提供的方格图十分相似，都有横轴、纵轴，绘制过程也都是先描点再连线。学生在没有领会图像本质的情况下，将画折线统计图的经验复制到正比例图像中，实在无可厚非。

2.射线——思维延伸的方向

思维能力的发展应该贯穿于整个数学学习过程中。教材中正比例图像的呈现是静止的，但其本质是运动的、变化的;绘制的图像看似是完整的，可它仍是局部的、可延伸的。图像需要延伸，学生的思维更应该在学习活动中不断延伸。借助表格的插入、数据的采集，让学生对正比例图像的理解由几个点变成多个点，再扩展为无数个点，最终形成一条线。由“线段”到“射线”的转变，其实就是学生心中正比例图像从静止走向运动，从离散走向连续、从运算走向关联的过程。思维的延伸还应体现在数形结合之中。“线段”向“射线”的变化过程不仅是图形的变化，还是数的变化。抽象的数据需要借助具体图像来展现，直观的图像同样需要丰富的数据来支撑。在正比例图像的形成过程中，学生能感受数与点的一一对应及连续性，把握数量间的变化规律，在运动与变化中概括、提炼和归纳并形成正确的表象，在数学语言与图表语言之间灵活转换，初步体会函数思想。

3.直线——经验积累的成功

从“线段”一端延伸成“射线”，再向另一端延伸发展为“直线”，这是学生的学习认知过程，也是学生理解函数思想的体验历程。函数是研究现实世界变量之间关系的一个重要模型，一直是中学数学学习的一个重要内容。而国际数学课程发展的趋势表明，对变量之间关系的探索可以从小学阶段开始。学生在教师创设的情境与活动经历中，感受到生活中存在着许多变量，体会到这些变量之间存在一定的关系，不仅积累经验，还与已有的经验进行比较，形成正确的认识，体会正比例图像和统计图的区别：折线统计图中的每一个统计数据是独立的，描出的点是离散的，而正比例图像中的量是变化的、连续的，点有无数个，也是连续的;折线统计图描述的是数据的变化及趋势，无须和原点相连，而正比例图像体现的是两个量之间相互依存的关系，是若干个点的集合，自然也包含（0，0）;折线统计图是根据实际情况进行的数据描述，呈现的数据是有限的、静止的，而正比例图像所包含的数据是无限的、运动的;折线统计图是对“数量”的描述，而正比例图像是对“关系”的探讨。这些经验的习得是有趣的、丰富的、自然的、水到渠成的，当然也是成功的！

（责编 李琪琦）