人工髋关节球形凹坑微织构表面摩擦学性能研究*

杨小洋 胡亚辉 毛璐璐 张春秋 郑清春

(1.天津理工大学天津市先进机电系统设计与智能控制重点实验室 天津 300384；2.机电工程国家级实验教学示范中心(天津理工大学) 天津 300384)

随着我国关节骨病发病率的增加，人工关节置换手术的临床运用越来越广泛。但相比于天然关节，由于一些主要结构的缺失，使得人工关节在减摩润滑性能上与天然关节存在一定差距[1-3]。因此研究改善人工关节的摩擦性能具有十分重要的意义。

大量的研究发现，适当的表面织构可以有效地改善摩擦表面间的摩擦性能[4-7]。WANG等[8]通过在SiC试样表面加工一系列直径和深度的织构并进行摩擦学实验发现，与无织构试样相比，不同参数的微织构均起到了一定程度的减摩作用。汪家道等[9]利用激光刻蚀在试样表面加工不同深度的微织构，通过对比其表面油膜压力发现，选择合适的微织构参数可以提高试样表面的油膜压力。 目前研究已经证明了可以通过加工微织构来改善人工髋关节的摩擦磨损性能。毛璐璐等[10]为改善钛合金人工髋关节假体的耐磨性，通过实验研究发现，加工合适的微织构参数可以有效降低钛合金的摩擦因数。奚铎闻等[11]利用数值方法研究球面纹理对人工髋关节润湿性能的影响，结果表明相对于光滑表面，带有微凸起的表面可以提升人工髋关节的承载能力。

MURAKAMI等[12]通过对椭圆形关节软骨标本进行实验发现，人在行走和跑步时关节处于流体润滑状态。由于人工关节在使用中大部分磨损发生在行走和跑步状态下。因此本文作者提出一种在人工髋关节表面加工球形凹坑微织构的方法来改善关节表面摩擦性能，并利用CFD数值仿真方法，对流体润滑状态下表面微织构参数对摩擦学性能的影响进行研究。

1 人工髋关节表面微织构CFD模型建立

1.1 微织构流域单元几何模型建立及参数设定

人工髋关节摩擦副表面间润滑油膜厚度为微米级，髋关节球头表面曲率半径远大于膜厚，故在此忽略摩擦副表面曲率的影响，将人工髋关节摩擦副表面简化成平面进行研究。简化后的微织构表面，如图1所示。将微织构单元所在区域上下摩擦副之间的流体区域定义为流域，取其中一个微织构流域单元作为研究对象，如图2所示。利用三维建模软件建立微织构流域单元的几何模型，微织构流域单元的长为a，宽为b，微织构沿速度方向的间距为c，织构直径为D，摩擦副上下表面间初始油膜厚度为h0，球形凹坑微织构深度为hp，织构最大深度为l。其中，流域单元长度为

图1 简化后微织构表面示意Fig 1 Schematic of micro texture surface after simplification

图2 微织构流域单元几何模型Fig 2 Geometric model of micro textured watershed unit(a) parameter setting of micro texture element；(b) schematic of film thickness

a=D+c

(1)

此外定义织构面积密度S为控制单元内微织构圆形开口面积占微织构单元面积的比值，微织构深径比hk为织构最大深度与织构直径的比值，其公式为

S=πD2/(4ab)

(2)

hk=l/D

(3)

1.2 基于Reynolds方程的润滑控制方程

建立人工关节摩擦副间润滑控制方程前做以下假设：

(1)人工关节摩擦副间被润滑液均匀分隔开，即处于全膜润滑状态；

(2)润滑液为不可压缩牛顿流体，采用层流方式；

(3)忽略流体的惯性力，忽略摩擦副间隙油膜两端压力差；

(4)摩擦副表面绝对光滑，流体与壁面接触无相对滑动。

得到简化后的Reynoleds方程[13]如下：

(4)

式中:h为润滑油膜厚度；η为润滑油黏度；U为滑动速度；p为油膜压力。

1.3 织构流域单元膜厚方程

取织构上表面为坐标平面，如图2所示，则摩擦副之间润滑液膜厚方程为

(5)

式中:h0为人工髋关节摩擦副上下表面间初始油膜厚度；Φ为微织构区域;hp为球形凹坑微织构深度，

(6)

1.4 微织构流域单元边界条件及网格划分

利用ICEM CFD进行前处理，首先将各边界单独建立为Part，在ANSYS Fluent中对相应的块设置边界条件，如图3所示。将垂直于速度U的入口、出口边界设置为周期性边界条件；将平行于速度U的前、后边界设置为对称边界条件；控制单元的上、下边界为无滑移壁面边界条件，其中下边界为固定壁面，上边界以速度U运动。

图3 微织构流域单元边界条件设置Fig 3 Boundary condition setting of micro texture watershed unit

之后利用ICEM CFD进行网格划分，采用有限体积法将计算流体域控制单元离散成为六面体结构性网格，网格将计算区域分割成35 000个足够小的计算区域，然后在每一个计算区域内应用流体控制方程求解，从而获得计算区域内的物理量分布。为保证计算的准确性，在计算前需检查网格质量。采用不可压缩牛顿流体作为连续相介质。压力-速度耦合格式设为SMIPLE；压力项选用PRESTO!离散，动量项采用二阶迎风格式离散，以保证求解过程的精确和稳定。

1.5 微织构流域单元CFD仿真结果

当摩擦副上表面以一定速度相对运动，由于润滑液黏性作用导致微织构表面间液体被带动，在摩擦副间形成楔形间隙，产生流体动压效应，同时由于润滑液黏性导致润滑液中剪切效应的产生。图4(a)、(b)所示分别为面积密度为15%、微织构深度为10 μm、速度为0.25 m/s条件下，球形凹坑微织构流域单元的压力分布和剪应力分布。

图4(a)所示为球形凹坑微织构单元压力分布云图。沿速度方向从左到右，在凹坑织构区域内，左端流入处由于上下表面间距增大形成发散楔导致压力下降产生负压，右端流出处由于上下表面间距减小形成收敛楔导致压力上升产生正压，正压最高值大于负压最低值。由于织构凹坑两侧正负压力差的存在使得流体流经织构摩擦副表面时形成动压效应，这对增加油膜平均承载力与减小摩擦因数从而改善摩擦副之间的摩擦性能起到积极作用[12]。

图4 球形凹坑微织构流域单元仿真结果Fig 4 Simulation results of watershed unit with micro texture ofspherical pit (a) pressure distribution(S=15%,l=10 μm,U=0.25 m/s)；(b) shear stress distribution(S=15%,l=10 μm,U=0.25 m/s)

1.6 CFD仿真实验验证

为验证仿真模拟结果的可靠性，将膜厚h0为6 μm的无织构流域模型的剪应力理论值与模拟值进行比较。无织构壁面剪应力的理论公式[14]如下：

(7)

式中：τ为理论公式计算的剪应力；du/dz为速度梯度。

式中速度梯度等于速度U与膜厚h0之比。由表1可知，在不同速度下模拟值与理论值相对误差约为1%，验证模拟方法的正确性。

表1 理论剪应力与模拟剪应力及误差对比Table 1 Comparison of theoretical shear stress and simulated shear stress and error

2 CFD仿真实验设计及数据处理

2.1 微织构流域单元CFD仿真实验设计

对单个微织构控制单元进行数值模拟计算，在此设置凹坑织构直径D与单元宽度b为固定值，分别为100、200 μm，油膜初始厚度h0取6 μm。各组微织构流域单元数据如表2所示。

表2 微织构流域单元参数设置Table 2 Parameter setting of micro texture watershed unit

润滑液黏度η设为0.05 Pa·s。在数值分析中将流体域单元上边界的滑动速度U分别设置为0.25、0.3、0.35、0.4 m/s，来研究不同速度下微织构参数对摩擦学性能的影响。

2.2 仿真结果数据处理

利用ANSYS Fluent分别对各微织构单元在不同速度条件下进行求解，利用Fluent自带后处理功能在织构控制单元内将压力p对控制单元下壁面进行积分得到油膜沿z方向的承载力F，以及微织构表面剪应力τ，之后通过计算得到单位面积内平均承载力Fa和微织构表面沿x方向摩擦力Ff，公式为

(8)

(9)

Fa=F/(ab)

(10)

将摩擦因数f定义为摩擦力与承载力之比，公式为

f=Ff/Fa

(11)

以平均承载力Fa和摩擦因数f作为衡量润滑性能的指标来分析微织构参数对摩擦学性能的影响。

3 结果与讨论

3.1 深径比hk对微织构表面摩擦学性能的影响

为讨论深径比hk对平均承载力Fa以及摩擦因数f的影响，选取微织构面积密度为10%的情况下，不同深径比的微织构流域单元作为研究对象。

不同速度下微织构深径比与平均承载力的关系，如图5所示。在深径比由0.06升高至0.12的过程中，各速度条件下的平均承载力均呈现出先下降后上升之后再下降的趋势。在所设速度范围内深径比为0.06的微织构表面平均承载力最高，深径比为0.12时的平均承载力最低。

图5 不同速度下深径比与平均承载力关系Fig 5 Relationship between depth diameter ratio andaverage bearing capacity at different speeds

图6所示为不同速度下摩擦因数与深径比的关系。可知，在同一深径比条件下织构表面摩擦因数随速度增加而降低。然而在相同速度下，在所设计的深径比范围内，摩擦因数随深径比增加呈现出先上升后下降再上升的波动趋势，其中深径比为0.06时微织构表面摩擦因数最低，当深径比达到0.12时微织构表面摩擦因数最高。

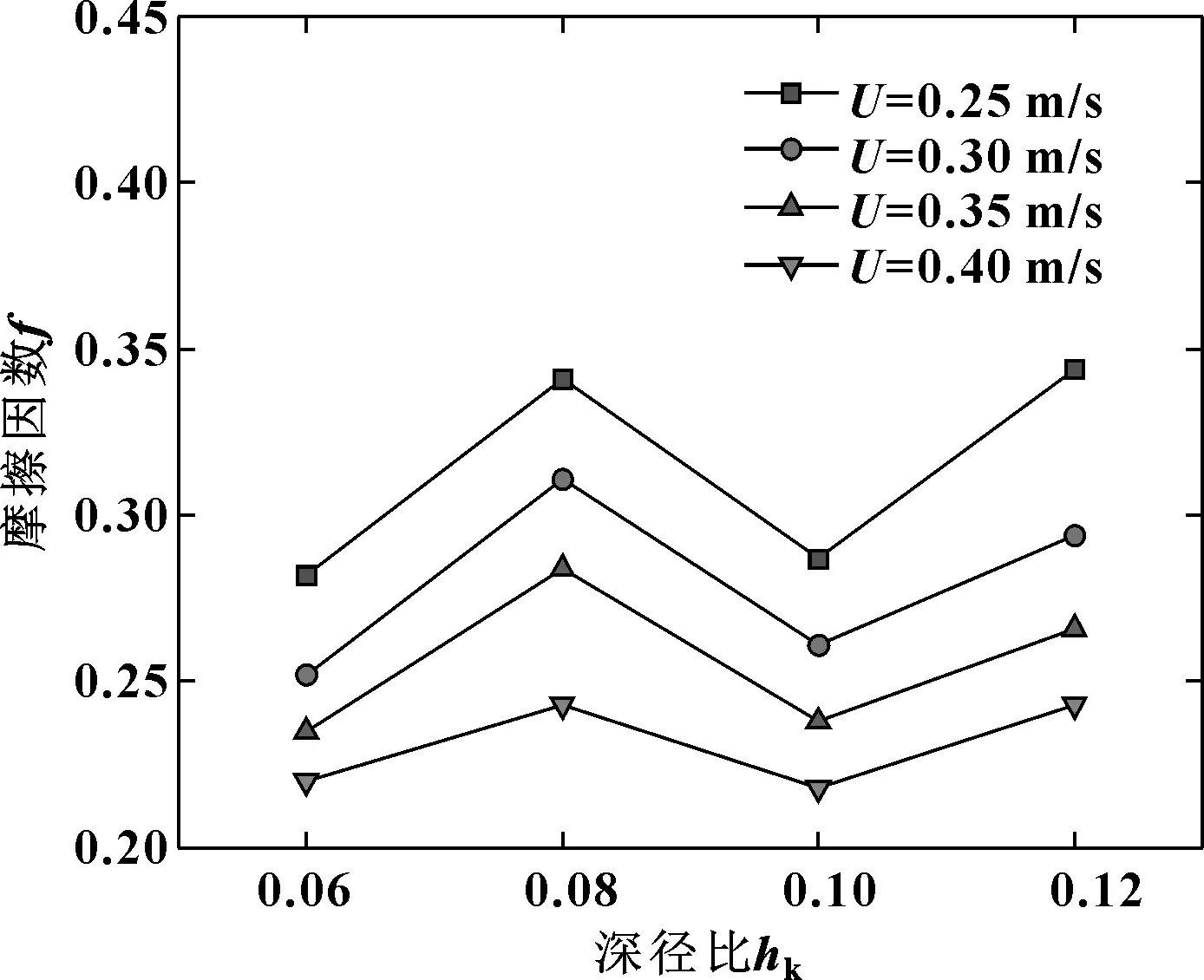
图6 不同速度下摩擦因数随深径比的变化Fig 6 Variation of friction coefficient with depthdiameter ratio at different speeds

一方面，随着微织构深径比的增加，由于流体剪切效应在微织构凹坑中产生的微涡流逐渐增强削弱了流体动压，从而导致平均承载力下降；另一方面，随着微织构深径比的增加，微织构中储存的润滑液也随之增加，可以为摩擦副提供更充足的润滑，这可能是导致深径比为0.10的表面织构比深径比为0.08的表面织构的摩擦因数低且产生的平均承载力高的原因。当深径比进一步增加时微织构中微涡流削弱作用的影响更加显著，这可能是导致深径比从0.10继续提高到0.12时摩擦因数上升且平均承载力下降的原因。

3.2 面积密度S对微织构表面摩擦学性能的影响

为讨论面积密度S对平均承载力Fa的影响，选取不同面积密度下深径比为0.10的微织构流域单元作为研究对象。

图7示出了在一定相对滑动速度下，在人工关节摩擦副表面设置球形凹坑微织构对摩擦副间油膜承载力的影响。可见，在所设速度范围内，平均承载力随着相对滑动速度的增加而增加；在相同速度条件下，随着微织构面积密度由5%升至30%，平均承载力呈现出先升高后降低的趋势，并在面积密度为10%时取得最高值。

图7 不同速度下面积密度与平均承载力关系Fig 7 Relationship between area density and averagebearing capacity at different speeds

图8反映出不同相对滑动速度下，摩擦因数与织构面积密度的关系。织构面积密度由5%增加到30%的过程中，摩擦因数呈现出先逐渐降低后缓慢上升的趋势，并在织构面积密度为25%时摩擦因数取得最低值，这与吴霄[13]所得模型及实验规律基本一致。

图8 不同速度下摩擦因数随面积密度的变化Fig 8 Variation of friction coefficient with areadensity at different speeds

随着织构面积密度的增加，流体动压润滑效应逐渐增强，导致平均承载力提高以及摩擦因数逐渐降低。当面积密度到达一定程度且继续增加时，织构沿相对滑动速度方向分布过于密集，导致难以建立稳定的润滑油膜[15]，这导致油膜承载力的下降以及摩擦因数的上升，且摩擦因数与面积密度的这一趋势随相对滑动速度的降低逐渐明显。对于平均承载力的最高值与摩擦因数的最低值对应的面积密度不一致这一问题，作者认为由于影响摩擦因数的因素有多种，平均承载力只是其中之一，由于面积密度的改变导致其他因素的变化，这可能是导致这一问题出现的原因。

4 结论

(1)在人工髋关节表面设置球形凹坑微织构可以提高油膜平均承载力降低摩擦因数，从而起到减小关节的摩擦磨损提高人工关节使用寿命的作用。

(2)摩擦副相对滑动速度对油膜平均承载力以及摩擦因数有明显影响，在所设速度范围内油膜平均承载力随速度提高而增加，摩擦因数随速度提高而减小。

(3)将深径比hk作为研究织构深度的参考值，研究发现在所设计深径比范围内，平均承载力先下降再上升最后再下降，摩擦因数呈现与平均承载力相反的波动趋势。当深径比为0.06时平均承载力最高，摩擦因数最低。

(4)在所设计面积密度范围内，平均承载力先上升再下降，摩擦因数先下降再上升。当面积密度为10%时平均承载力最高，面积密度为25%时摩擦因数最低。

(5)利用CFD数值仿真方法研究微织构参数对人工骨关节摩擦学性能影响的方法是可行的，为今后进一步开展相关研究奠定了一定基础。