等相对曲率齿轮磨损性能研究*

倪佳乐 刘 雷

(南京航空航天大学机电学院 江苏南京 210000)

齿轮传动是机械装置中最为常见的传动形式，其中渐开线齿廓齿轮因其出色的性能而被广泛运用，但同时该齿轮也有着一定的局限性，因此新型齿轮齿廓一直是齿轮研究的一个重要方向。刘雷提出了等相对曲率(CRC)齿轮[1]，相较于渐开线齿轮，该新型齿轮具有如下优势：齿面接触强度有所提升，齿面应力分布不均的问题得到改善；齿轮具有较小的滑动系数，可有效减小齿面磨损；齿间最小油膜厚度得到了提高，改善了齿面润滑效果。LIU等[1]通过对齿面滑动系数以及最小油膜厚度的计算,从侧面展现了CRC齿轮的磨损性能，但缺少直接且准确的磨损性能研究结果。因此本文作者将通过齿面磨损量的计算，对CRC齿轮的磨损性能展开更直接的理论研究。

齿轮磨损在传动过程中长久存在且不可避免，并且磨损量在累积之后会对齿轮传动效率、传动精度以及齿轮啮合刚度造成影响[2]，缩短齿轮的使用寿命，加速轮齿的失效；过度的磨损甚至会导致轮齿断裂从而发生事故[3]；此外，齿面的磨损亦会对齿轮系统的动态特性产生影响，从而激励系统产生振动与噪声[4]。随着齿轮向高速、重载、精密、高效与低噪等方向发展[5]，传动系统对耐磨性的需求急剧增强。因此，对于齿轮磨损性能的研究有着很大的现实意义。

针对齿轮磨损的研究理论非常丰富，但主要分为以下3种：

(1)基于黏着磨损理论的齿轮磨损计算。国内外对于黏着磨损理论的研究大多基于Archard黏着磨损通式。在该理论的基础上，ANDERSON和ERIKSSON[6]提出了单点观测法，将啮合过程离散为有限个观测点，对每个观测点都进行单独的磨损计算，同时还推导了滑动距离的解析计算式；FLODIN和ANDERSSON[7]则考虑了单点观测法中单次啮合过程的接触压力和滑动速度的变化；LUNDVALL和KLARBRING[8]在此之上引入有限元法来计算直齿轮的齿面接触压力和滑动距离。

(2)基于疲劳磨损理论的齿轮磨损计算。克拉盖尔斯基率先提出了疲劳磨损的计算公式。潘尔顺等[9]基于边界元理论，提出用三次样条曲线拟合磨损后的齿面，结合克拉盖尔斯基的疲劳磨损计算式，分析直齿轮的疲劳磨损。王淑仁等[10]根据齿面疲劳磨损与剥层磨损机制的相似性，建立了闭式齿轮传动的疲劳磨损模型，给出了相关参数的计算方法。

(3)基于能量磨损理论的齿轮磨损计算。1973年，FLEISHER提出了能量磨损理论[11]，并给出了摩擦功与磨损体积的关系式。该理论的基本观点是：摩擦功大部分以热能的形式散失，但仍有少部分以势能的形式储存在摩擦配副材料中；当一定体积的材料储能达到临界值时，则以磨屑或磨粒的形式从基础表面剥落。章易程等[12]根据该理论推导了基于摩擦功原理的高副滑动磨损计算式。

CRC齿轮齿型不同于渐开线齿轮，其啮合线不是直线，这增加了齿轮磨损量计算的难度。鉴于此，本文作者通过建立CRC齿轮的数学模型，根据数学模型获得齿廓上各点的坐标，精确求解相关几何参数，分别基于克拉盖尔斯基磨损计算方法及Archard磨损计算方法对CRC齿轮的磨损量进行了计算，并与相同参数的渐开线齿轮的磨损情况作对比分析。

1 CRC齿轮数学模型

图1示出了齿廓啮合原理，坐标系定义如下：S(Oxy)固定坐标系原点位于节点P，转动坐标系S1(O1x1y1)、S2(O2x2y2)分别与主动齿轮与从动齿轮固结，原点分别位于齿轮的转动中心，移动坐标系S3(O3x3y3)与产形齿条固结。由图1可知，在起始位置Ⅰ处，主动轮齿廓Σ1、从动轮齿廓Σ2与产形齿条齿廓Σ3啮合于啮合线上一点A。若此时虚拟齿条向左移动距离L，则Σ1将逆时针旋转角度φ1与Σ3啮合于点b。因此，主动齿廓在起始位置的对应点B1可通过将啮合点b绕原点O1顺时针旋转角度φ1得到，主动轮齿廓点B1在S1系中的坐标如下：

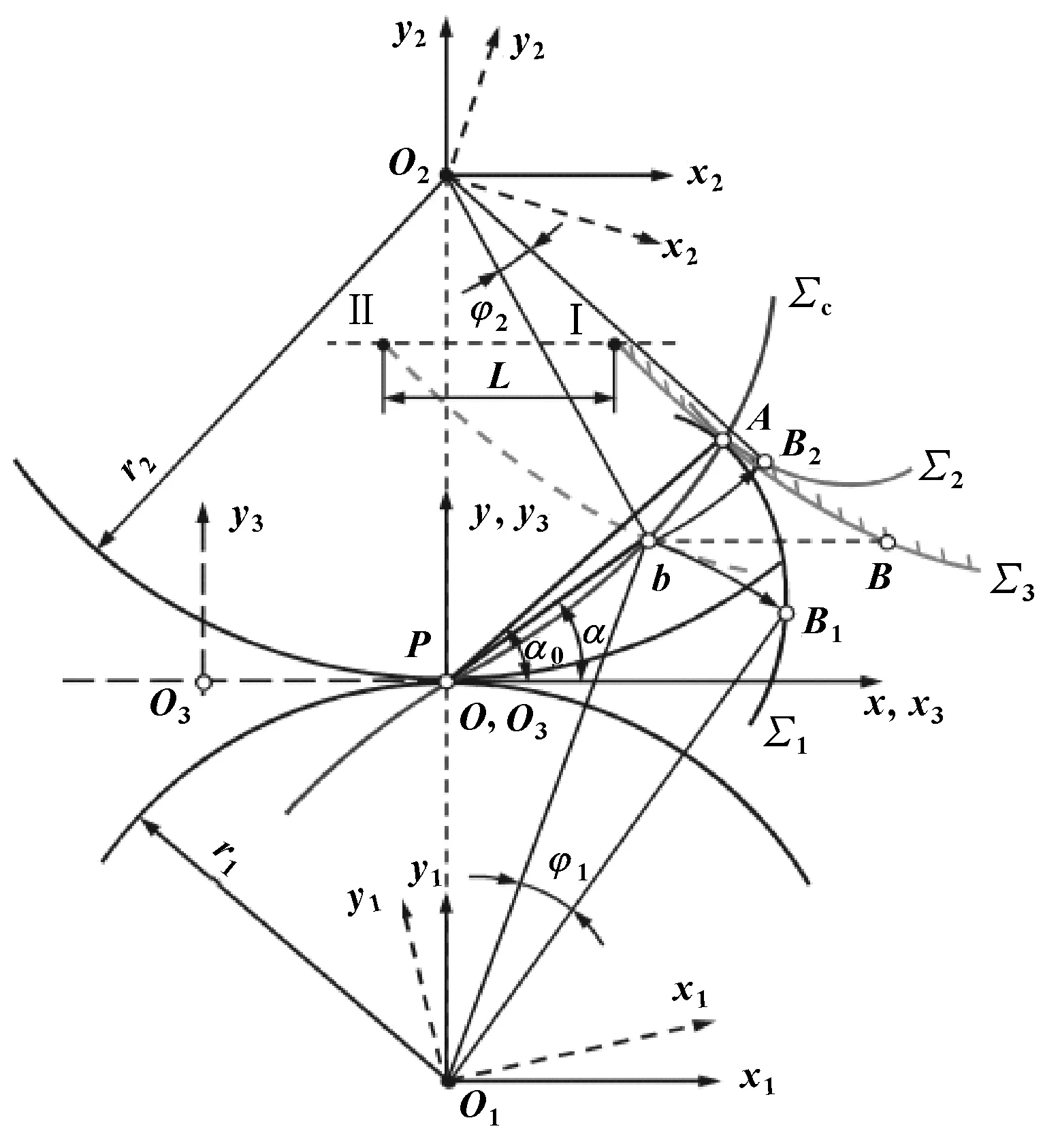
图1 基于啮合线的齿廓设计Fig 1 Design of tooth profiles based on path of contact

(1)

式中：r表示原点O到点b的距离；α表示原点O与点b的连线与x轴正方向的夹角；r1表示主动轮的节圆半径。

同理，可得从动齿廓点B2在S2系中的坐标为

(2)

式中：r2表示从动轮的节圆半径。

CRC齿轮的设计核心在于控制齿轮啮合过程中的相对曲率保持不变，且该曲率为相同设计参数下渐开线齿轮啮合过程中相对曲率的最小值Kr，min。由微分几何得齿轮1齿廓的曲率：

(3)

式中:x′1、x″1、y′1、y″1为x1、y1对α的一阶导数和二阶导数。

(4)

(5)

其中

(6)

(7)

(8)

将式(4)—(8)代入式(3)可以得到

(9)

同理，可得齿轮2齿廓的曲率：

(10)

当齿轮啮合位置处于第一或第二象限时，啮合点的共轭齿廓相对曲率[1]可以表示为

Kr=k1-k2=

Kr,min

(11)

令t=sinα可得：

(12)

(13)

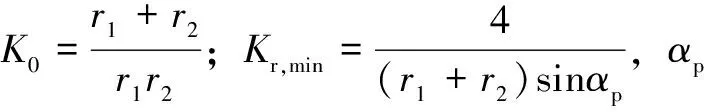
对式(13)求数值解,可求得关于t的多项式表达如下：

t=sinα=anrn+an-1rn-1+…+a1r+a0

(14)

式中：an,an-1,…,a0为多项式系数。

同理可得，当齿轮啮合位置处于第三或第四象限时，微分方程则表示为

(15)

此时t的解可以表示为

t=sinα=bnrn+bn-1rn-1+…+b1r+b0

(16)

式中：bn,bn-1,…,b0为多项式系数。

当啮合线位于第Ι、Ш象限时，在一个啮合周期内起始啮合点、终止啮合点由以下方程确定：

(17)

(18)

式中：rⅠ、rⅡ分别表示起始啮合点、终止啮合点到坐标原点o的距离。

将式(14)(16)代入上式(17)(18)即可求解得到rⅠ、rⅡ的数值解。

由平面齿廓啮合定律可知，

(19)

故在啮合过程中不同啮合位置上的旋转角度的值可表示为

(20)

至此，就得到了CRC齿轮的主动轮齿廓Σ1、从动轮齿廓Σ2与产形齿条齿廓Σ3的数学表达式。

2 磨损计算模型

2.1 基于克拉盖尔斯基磨损公式的计算方法

基于克拉盖尔斯基提出的疲劳磨损计算式[13]，齿轮疲劳磨损计算模型如图2所示。

图2 疲劳磨损计算模型Fig 2 Fatigue wear calculation model

在某一啮合时刻，主动轮上点a1开始进入啮合，此时与从动轮上点b1重合接触。经过一定的时间之后，主动轮上的点a1运动到了点a′1,且即将退出啮合，而此时从动轮上的点b1运动到了点b′1。在整个运动过程中，点a1的移动距离记为Sa1，点b1的移动距离记为Sb1，如图2可知，此时滑动距离S可以表示为

S=|Sa1-Sb1|

(21)

根据滑动系数的定义，可以得到主动轮的滑动系数λ为

(22)

同时，主动轮上点a1的移动距离可以表示为Hertz接触半宽aH的2倍，即

Sa1=2aH

(23)

因此在一次啮合过程中接触区内单点的滑动距离S可以表示为

S=2aHλ

(24)

传动运转周期内总的滑动距离为

L=Sntεα

(25)

式中：n为转速；t为运转时间；εα为重合度。

磨损深度为

h=Ih·L

(26)

疲劳磨损深度表达式为

h=2IhaHλntεαWMWLWP

(27)

式中：Ih为磨损率；WM、WL与WP分别为齿面改性系数、润滑系数和载荷系数，但文中不做考虑，其值均取为1。

2.2 基于Archard通式的磨损计算公式

广义的Archard磨损计算通式[14]可以表达为

(28)

式中：V为磨损体积；S为滑动距离；W为法向载荷；H为观测表面的材料硬度；K为无量纲磨损系数。

式(28)经过变换，可得摩擦副表面任意一点P处的磨损深度

(29)

式中：k为有量纲的磨损系数；p为计算点处的接触压力。

ANDERSON和ERIKSSON[6]将式(29)运用到了直齿轮的磨损计算中，并提出了单点观测法。即把啮合齿面离散成有限个观测点，通过单独计算每个观察点的磨损深度来表征黏着点齿面的磨损分布。该方法假设观测点在单次啮合过程中接触压力保持不变且滑动距离为定值，故观测点P处的磨损深度可表示为

hP,n=hP,(n-1)+kpP,nSP

(30)

式中：hP,n和hP,(n-1)分别表示第n次和第n-1次啮合后点P处的磨损深度；pP,n为第n次啮合时点P的接触压力；SP为点P单次啮合的滑动距离。

ANDERSON在其博士论文中将啮合轮齿等效为半径连续变化的一对圆柱体接触，推导出了滑动距离SP的解析式[15]

(31)

式中：SP1和SP2分别为主动轮和从动轮在接触点处的滑动距离;vP1和vP2分别为两齿轮在接触点处的切向速度;aH为Hertz接触半宽。

啮合接触点i表面压力可以根据Winkler接触模型确定[16]

(32)

其中

(33)

(34)

(35)

式中：R为啮合处的相对半径；E*为等效弹性模量；aH为Hertz接触半宽；E1、E2、μ1、μ2分别为主动轮与从动轮的弹性模量和泊松比；Kr为啮合处的相对曲率半径，文中设为常量。

3 算例

表1列出了文中齿轮对磨损计算参数，并且分别使用基于克拉盖尔斯基的疲劳磨损理论公式(以下简称方法一)及基于Archard磨损通式的黏着磨损理论公式(以下简称方法二)在MATLAB中进行计算。为了保证2种方法结果对比的可信度，在运算中需要保证单个齿面接触次数保持一致。所以文中计算时，将基于克拉盖尔斯基磨损公式中的运行时间t设定为600 min，同时将基于Archard磨损通式的计算式中磨损次数设为576 000次，即运行时间t乘上小齿轮转速n1的值。

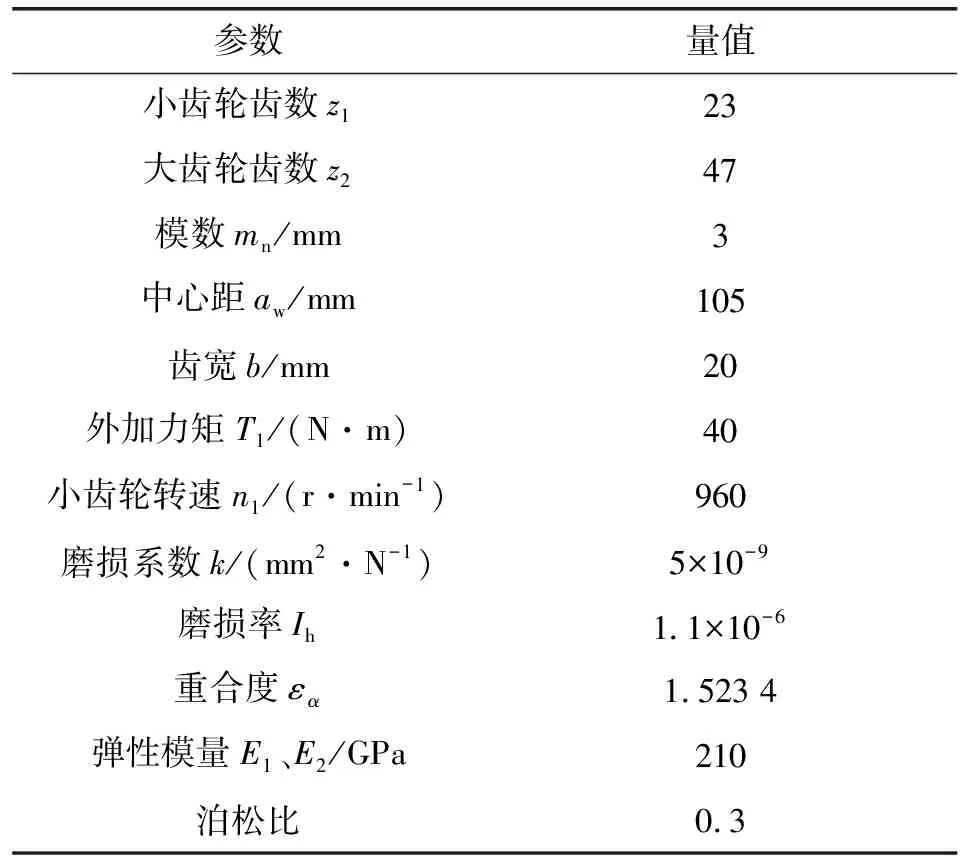
表1 齿轮设计参数Table 1 Gear design parameters

根据第1节的CRC齿轮齿廓计算方法，在MATLAB中使用表1中的参数进行计算后，可以得到如图3所示的在节点处啮合的CRC齿轮齿廓，图中左侧为小齿轮齿廓，右侧为大齿轮齿廓。

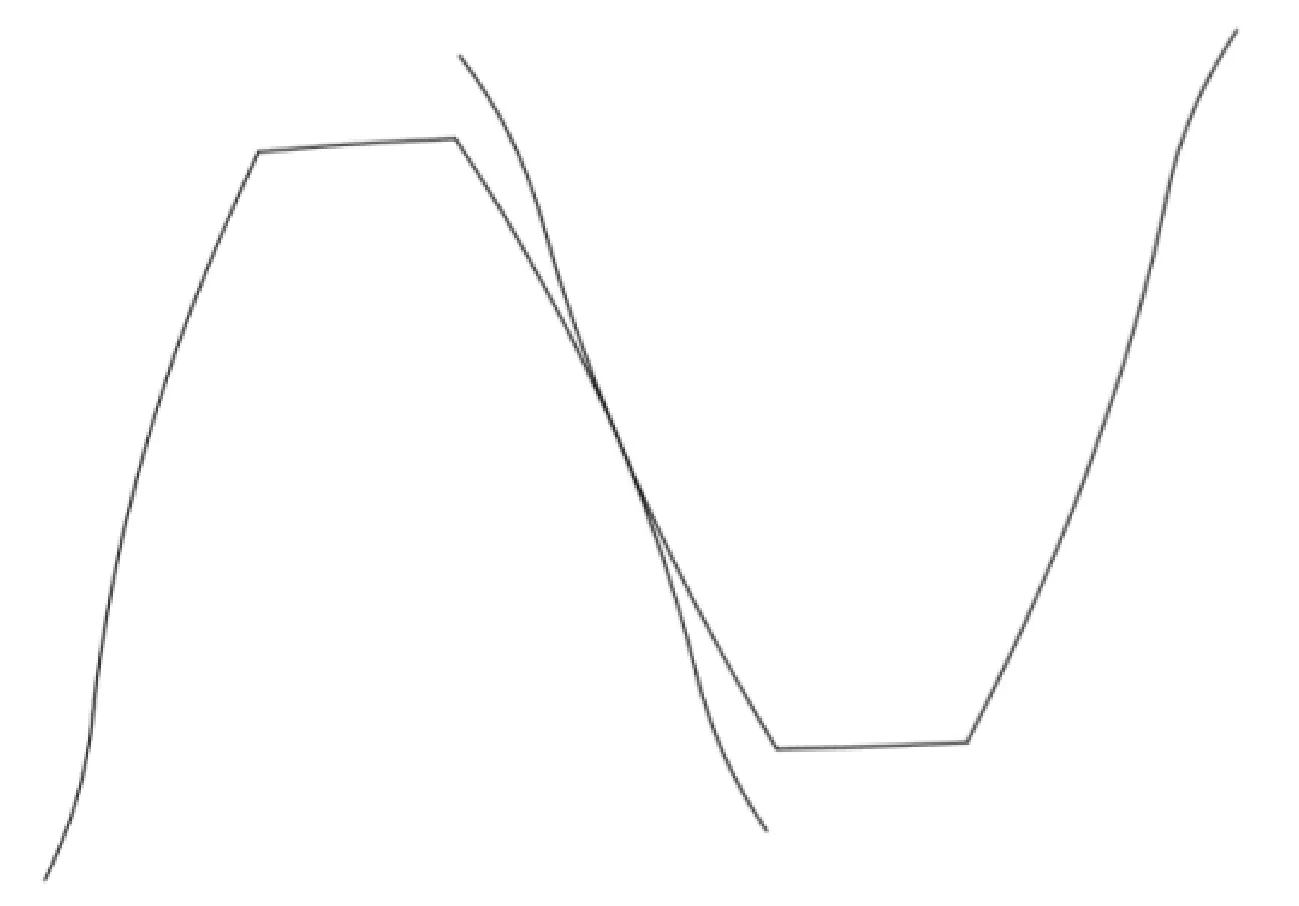
图3 节点处啮合的CRC齿轮齿廓Fig 3 The tooth profile of the CRC gear meshed at the node

在得到CRC齿轮齿廓之后，采用将单个轮齿简化为非均匀悬臂梁的刚度计算模型，并使用能量法对单个轮齿的刚度进行计算。在分别求得主动轮与从动轮的单齿刚度之后，就可以计算得到单对齿啮合刚度以及齿轮综合刚度。综合刚度如图4所示。图中横坐标代表从节点处到啮合点的主动轮旋转角度，正负代表不同的旋转方向，啮合顺序为从横坐标的负值开始向正值方向啮合，即最左端为啮合起始点，最右端为啮合终止点。图中的突变是由单双齿啮合转换产生的，两侧为双齿啮合区齿轮综合刚度，中间为单齿啮合区齿轮综合刚度。

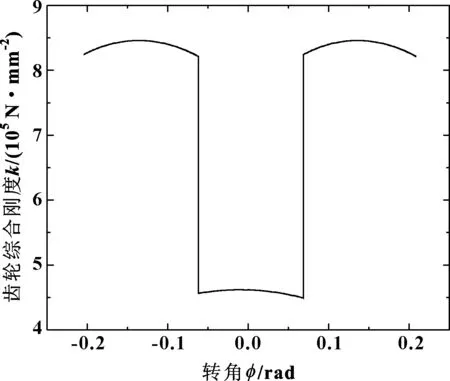
图4 CRC齿轮综合刚度Fig 4 Comprehensive stiffness of CRC gear

在得到单对齿啮合刚度的基础上，根据齿间载荷分配计算方法可以获得CRC齿轮轮齿在单次啮合中的齿间载荷分配率，如图5所示。

图5 CRC齿轮载荷分配率Fig 5 CRC gear load distribution rate

图6分别展示了CRC齿轮与渐开线齿轮的主动轮和从动轮的滑动系数。可以发现，CRC齿轮整体的滑动系数均小于渐开线齿轮，相应的滑动距离也就更短。滑动距离是计算磨损深度的重要参数，因此仅从滑动系数就可以初步发现CRC齿轮磨损性能较渐开线齿轮更优秀。

图6 CRC齿轮与渐开线齿轮滑动系数Fig 6 Sliding coefficients of CRC gear and involute gear

图7示出了使用方法一计算得到的经过600 min的磨损之后，主动轮和从动轮齿廓上的磨损深度曲线。图中从左往右为齿轮啮合顺序，即图中最左端为主动轮齿根处及从动轮齿顶处，最右端则为主动轮齿顶处及从动轮齿根处。主动轮与从动轮的磨损量均在齿根处达到最大，而齿顶处相对较小，且在单双齿变换处发生突变。

图7 CRC齿轮基于方法一的磨损曲线Fig 7 Wear curves of CRC gear based on method 1

图8与图9所示分别为使用方法二得到的在经过576 000次磨损之后，主动轮和从动轮齿廓上的磨损深度曲线。图8显示了主动轮齿面从0开始每经过3 600次啮合之后的磨损深度变化曲线，即每两条磨损曲线之间啮合次数相差3 600次，且从上到下啮合次数逐渐增加。而图9则是从动轮磨损曲线，每条磨损曲线之间的啮合间隔为1 500次。

图8 CRC齿轮主动轮基于方法二的磨损曲线Fig 8 Wear curves of CRC gear driving wheel based on method 2

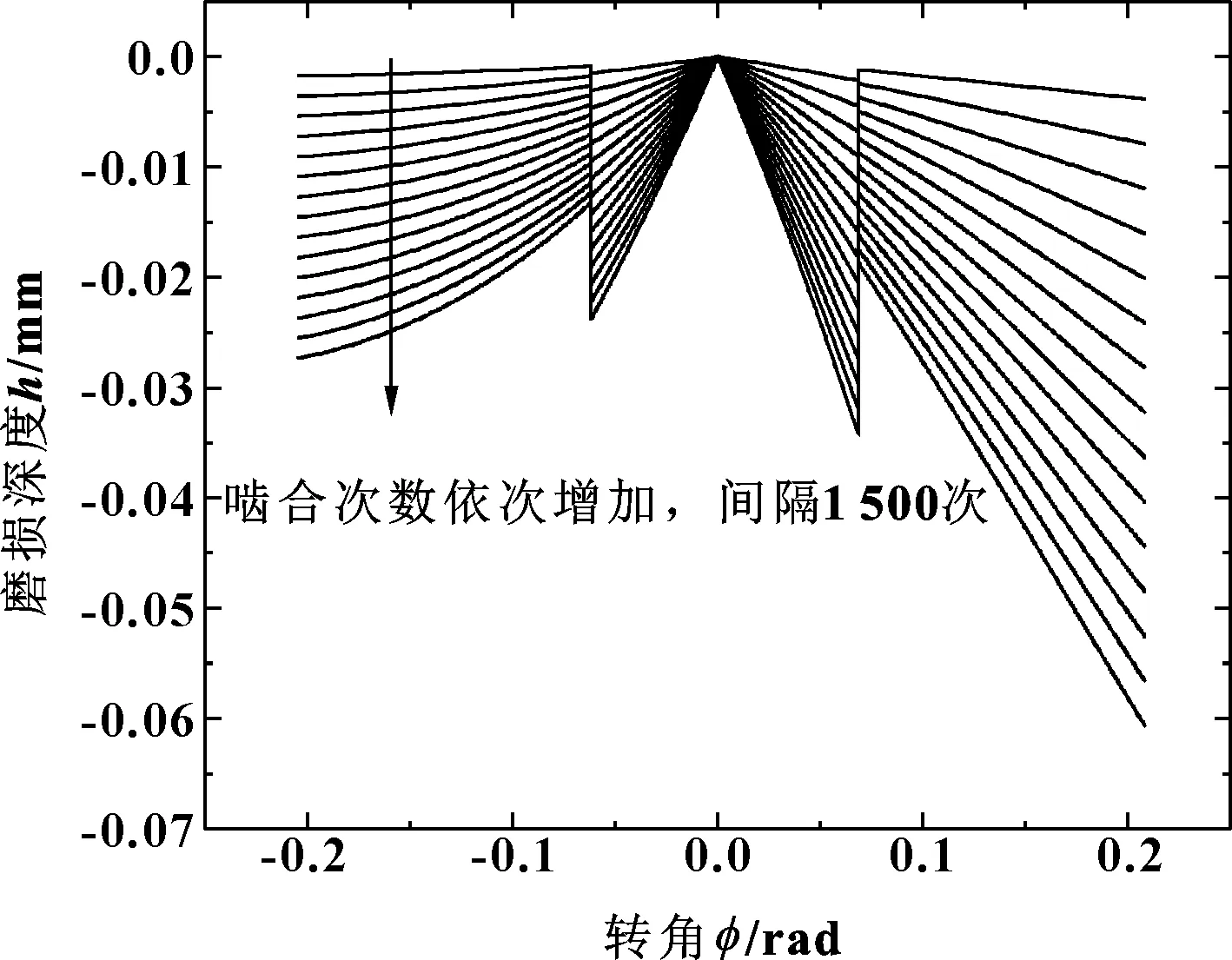
图9 CRC齿轮从动轮基于方法二的磨损曲线Fig 9 Wear curves of CRC gear driven wheel based on method 2

对2种方法的结果进行简单的比较，可以发现它们具有相同的变化趋势且最大磨损深度值相当接近，因此可以认为方法一及方法二得到的结果具有一定研究价值。同时，观察方法一与方法二的磨损曲线图，可发现无论是主动轮还是从动轮，最大磨损都发生在齿根处，节点处的磨损最小，且主动轮的磨损要大于从动轮的磨损。因为考虑了齿间载荷分配率的影响，磨损曲线上在单双齿变化处产生了突变。这一系列特点都与渐开线齿轮保持了一致性。

图10所示为相同设计参数下的渐开线齿轮使用方法一计算得到的磨损变化曲线，这与文献[17]得到的结果相一致，验证了文中计算结果。从图10中可以很清楚地看到，渐开线齿轮主动轮的最大磨损值达到了0.19 mm，远大于CRC齿轮的主动轮的最大磨损值0.1 mm(如图7所示)。而在齿顶处CRC齿轮的磨损量与渐开线齿轮的磨损量是较为一致的，都是在0.06 mm左右，这一点与图11中CRC齿轮与渐开线齿轮的相对曲率曲线趋势保持一致。相较于主动轮，从动轮的磨损量相差不大，且在齿顶处磨损量差值达到最大。据此可以发现，相对曲率对齿轮磨损有着相当大影响，相同啮合位置处相对曲率越大磨损会越严重。而CRC齿轮由于在啮合过程中保持相对曲率不变，且该相对曲率为相同参数下渐开线齿轮啮合过程中相对曲率的最小值，因此CRC齿轮的整体磨损量较渐开线齿轮要小很多，且磨损量相差的最大值在渐开线齿轮相对曲率最大处取得，即主动轮齿根处及从动轮齿顶处。

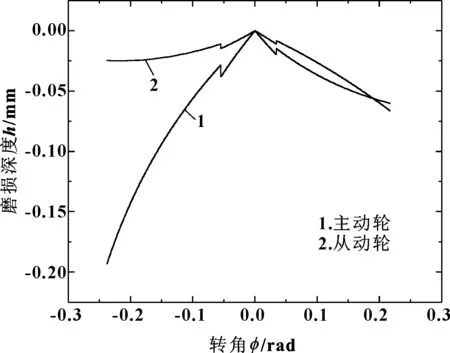
图10 渐开线齿轮基于方法一的磨损曲线Fig 10 Wear curves of involute gear based on method 1

图11 CRC齿轮与渐开线齿轮的相对曲率Fig 11 Relative curvature of CRC gear and involute gear

4 结论

(1)CRC齿轮齿面磨损曲线变化趋势与渐开线齿轮一致，表现为齿根处磨损大于齿顶处，主动轮磨损大于从动轮，且节点处磨损值最小。

(2)CRC齿轮磨损量较渐开线齿轮要小很多，特别是主动轮齿根处及从动轮齿顶处，表明CRC齿轮的磨损性能较渐开线齿轮有着较大的提升。

(3)相对曲率对齿轮磨损有着相当大影响，相同啮合位置处相对曲率越大磨损会越严重。与渐开线齿轮相比，CRC齿轮由于保持了相对曲率不变且为一较小值，因此整个齿面上的磨损量变化更小。