一类混杂系统的充分最优性条件
李丽花
(上海电力大学 数理学院, 上海 200090)
随着计算机技术的广泛应用和现代工业的快速发展,系统结构变得越来越复杂,大多数的复杂控制系统都含有连续变量的动态变化过程和以符号操作为特征的离散过程。这种由连续演化和离散演化混合而成,且两者相互作用的复杂系统,称为混杂系统。作为混杂系统研究领域的一个重要组成部分,混杂系统的最优控制引起了研究者的广泛关注[1-8]。
目前,对混杂系统最优控制问题的研究大都集中在必要最优性条件[2-8]。利用混杂最优控制问题的解所满足的必要条件,可以得到可能的最优解。该解是否真的最优还需要充分条件来保证。对于一类连续系统的最优控制问题,通过将Hamilton-Jacobi不等式的求解转化成求解一个有限维参数优化问题,可以得到该问题最优解所满足的充分条件[9]。该充分条件主要包括Legendre-Clebsch条件和Riccati方程的求解,相对易于验证。对于混杂最优控制问题,其难点在于确定Riccati方程所满足的跳跃性条件。本文利用参数化方法,将系统状态产生跳跃的点转化为待确定的参数,求出了满足特定边界条件的Riccati矩阵方程,得到了一类混杂最优控制问题的最优解所满足的充分条件,将连续系统的Riccati方法推广到混杂系统。
1 问题描述
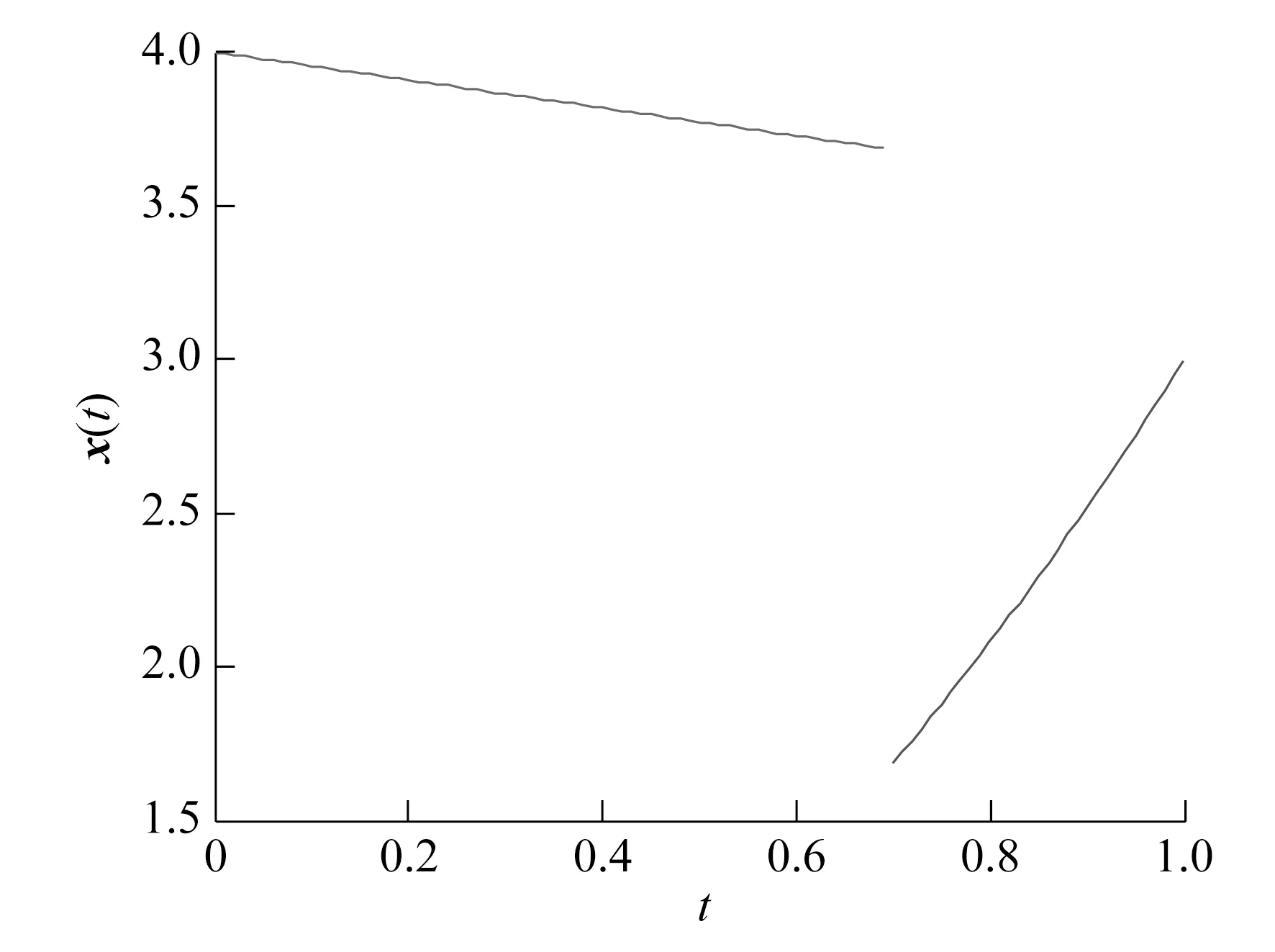
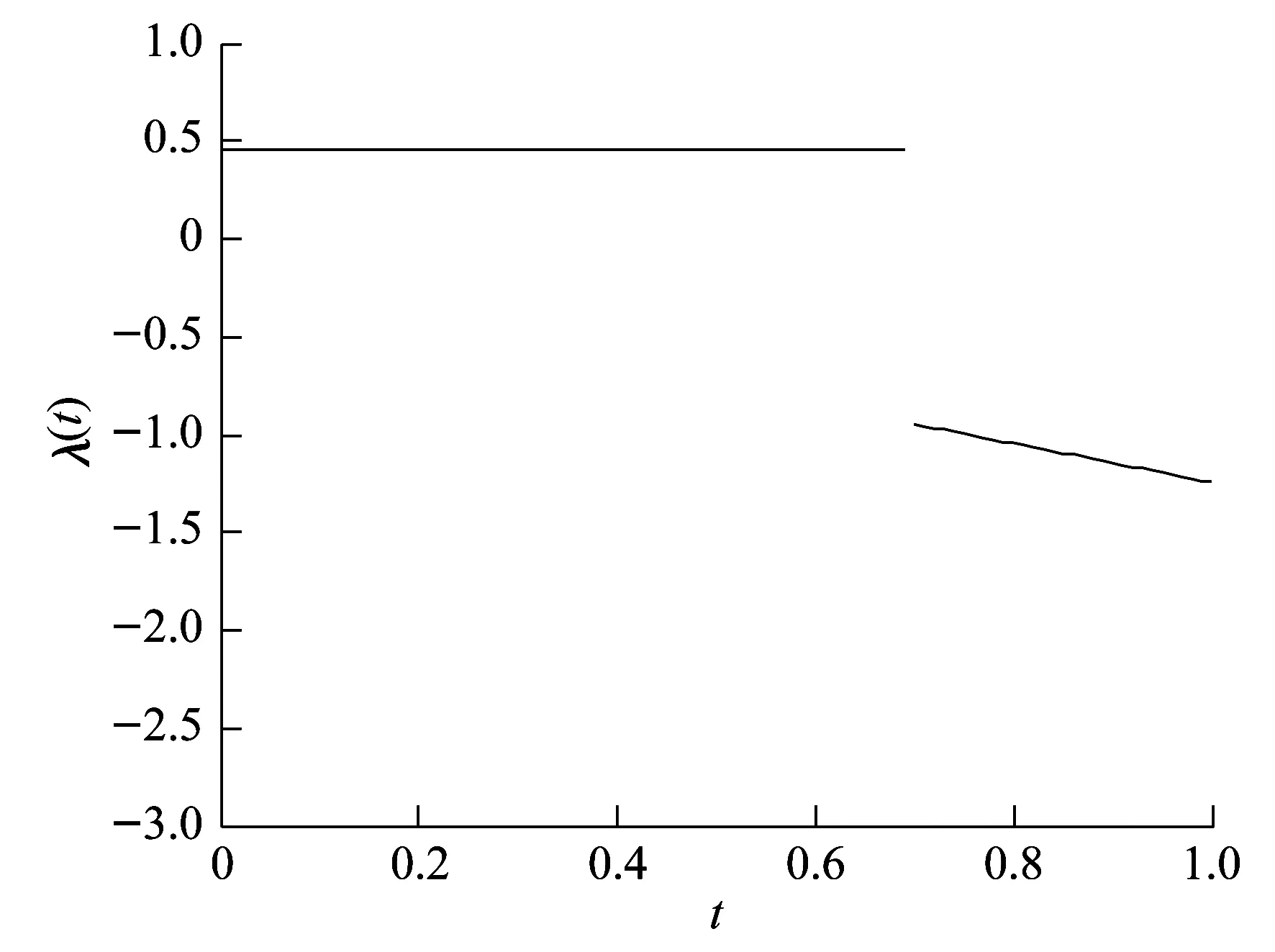
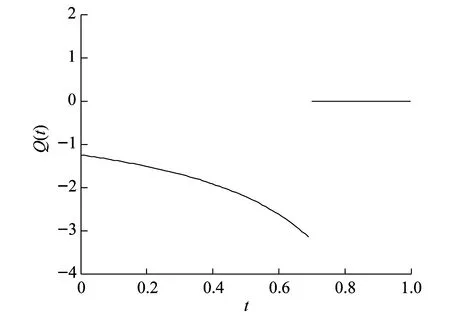
设t0 (1) 记θ=(t1,t2,t3,…,tN-1),则确定满足式(1)的向量组(θ,x(t),u(t)),使得函数 (2) 为最小。 其中,φi∈R,Li∈R,关于其变量二次连续可微,i=1,2,3,…,N。 为方便起见,记上述最优控制问题为(P)。 定理1设 (θ0,x0,u0)为最优控制问题(P)的极小值,则存在λ0∈R和分段连续变量λ(t)=(λ1(t),…,λN(t))T,使 Hi(x(t),u(t),λi(t))= i=1,2,3,…,N (3) 则以下结论成立: (1) 协态方程 (4) (2) 极小值条件 (5) (3) 连续性条件 i=1,2,3,…,N-1 (6) (4) 跳跃性条件 i=1,2,3,…,N-1 (7) 定理1的证明与文献[8]中类似。定理1给出了最优控制问题(P)的必要性条件。利用必要性条件得到的最优解是否真的最优,还需要进一步判断。下面给出判断该最优控制问题(P)的最优解的充分条件。 定理2设(θ0,x0,u0)满足定理1中的一阶必要性条件,若以下条件成立 (8) (Hixu+Qifiu)(Hiuu)-1· (Hixu+Qifiu) (9) (Hixu+Qifiu)(Hiuu)-1· (10) (11) 其中,τi=ti-ti-1,Qi(t)∈Rn×n,Ri(t)∈Rn,qi(t)∈R。 (3) 式(8)~式(10)的解Qi(t),Ri(t)和qi(t)满足如下边界条件和跳跃条件: 证 明对i=1,2,3,…,N, 记τi=ti-ti-1,通过t=ti-1+sτi引入变量s∈[0,1],定义为 xi(s)=x(ti-1+s(ti-ti-1)) (12) ui(s)=u(ti-1+s(ti-ti-1)) (13) 可以将最优控制问题(P)转化为等价问题(P1),即 (14) τNHNuNuN) (15) (16) (17) 同时,可以得到 (18) (19) (20) i=1,2,3,…,N (21) 利用式(5)~式(7),可以得到等价问题(P1)的Riccati微分方程,为 (22) (23) 对i=1,2,3,…,N,记 (24) (25) 定理2表明,最优控制问题(P)的充分条件判别在于满足一定边界条件和跳跃条件的Riccati矩阵方程组解的存在性的判别,以及Hamilton方程Legendre-Clebsch条件的验证。 (26) 该最优控制问题的Hamilton函数为 (24) 根据定理1,经计算可得,当v=-2时,该混杂系统的最优跳变时刻为t1=0.699 3,系统的控制变量、状态变量和协态变量曲线如图1~图3所示。 图1 控制变量曲线 图2 状态变量曲线 图3 协态变量曲线 利用定理2检验跳变时刻t1=0.699 3的最优性。因为该最优解是用定理1的结论计算所得,因此一阶必要条件满足。 此外,在区间[0,1]上,有Hiuiui=1>0,i=1,2,故式(8)成立。 由式(9)~式(11)可得 (28) (29) (30) 通过选取适当的参数,式(28)~式(30)有如下解 (31) (32) (33) 记 (34) (35) (36) 函数Q,R,q的图形如图4~图6所示。由图4~图6可知,定理2中的第2个条件满足。 图4 函数Q的图形 图5 函数R的图形 图6 函数q的图形 (37) 式(32)的特征值为0.060 1,3.103 9,6.513 8,所以该矩阵在R3×R3上正定,跳跃条件B2满足。这样定理2的条件都满足了,因此t1=0.699 3最优。 本文研究了一类混杂系统的最优控制问题。通过将系统状态跳变时刻为端点的可变子区间转化为新的状态变量,再利用古典的最优控制理论,得到了该混杂控制问题最优解所满足的充分条件。结论表明,当Legendre-Clebsch条件成立,且满足特定条件的Riccati方程存在有界解时,利用必要性条件求出来的最优解为真正的最优解。本文的结论将最优控制的充分条件从连续系统推广到混杂系统。2 主要结论及其证明

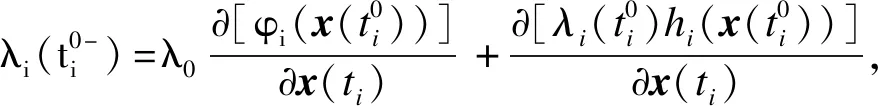

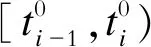


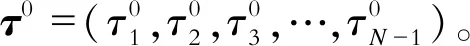

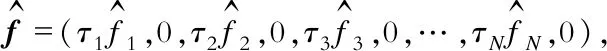
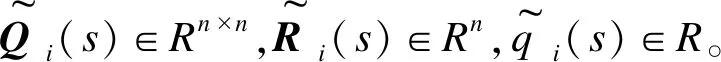
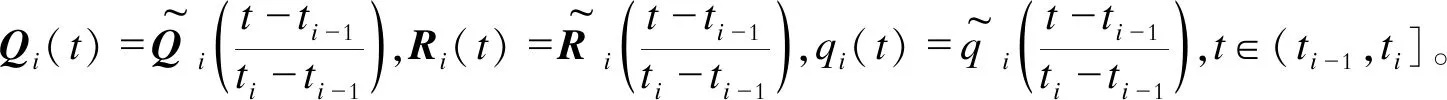


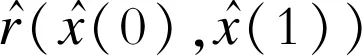
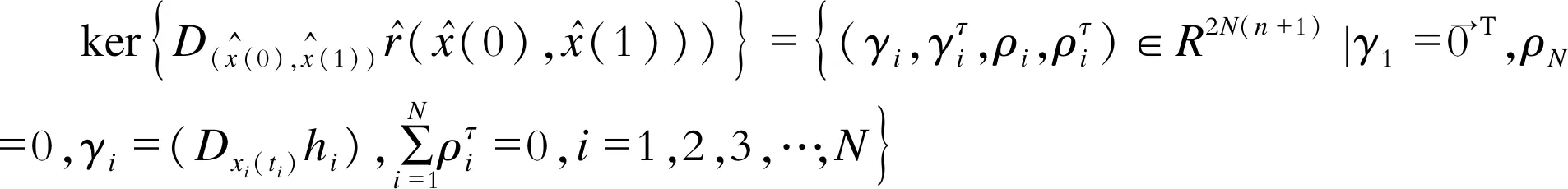
3 举 例



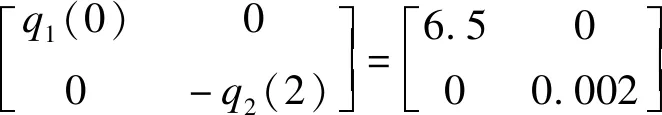

4 结 语
- 上海电力大学学报的其它文章
- 隐马尔可夫模型的构建及实现
- 多方控制的多粒子未知态双向量子隐形传态方案

