隐马尔可夫模型的构建及实现

刘 辉

(上海电力大学 计算机科学与技术学院, 上海 200090)

隐马尔可夫是可用于标准问题的统计学习模型,描述由隐藏的马尔可夫链随机生成观测序列的过程,属于生成模型[1]。其难点是从可观察的参数中确定该过程的隐含参数,然后利用这些参数来作进一步的分析,例如模式识别。藏于物理世界中的往往是表象,而真正的隐藏状态是不可见的,需要通过观察大量的表象来总结规律,从而确定事物的隐含状态,认识事物的本质。事物的隐含状态与事物的表象存在着一定的关联关系,可以通过统计的方法来确立它们之间的关联。

1 隐马尔可夫模型的建立

1.1 建立训练数据集

在隐马尔可夫模型的定义中,Q={q1,q2,q3,…,qN}是所有可能的状态集合,V={v1,v2,v3,…,vM}是所有可能的观测集合,I={i1,i2,i3,…,iT}是长度为T的状态序列,O={o1,o2,o3,…,oT}是对应的观测序列。

本文通过观察海藻湿度的状态,确定是雨天还是晴天的例子来推导隐马尔可夫模型的计算推理过程。海藻的湿度为可见状态,而天气状况为隐藏状态(假设盲人能够感知海藻湿度,却无法观察天气)。在海藻模型中,观测概率矩阵为

B=[bj(k)]N×M

(1)

式中:bj(k)——在时刻t处于状态qj的条件下生成观测vk的概率,bj(k)=P(ot=vk|it=qj),k=1,2,3,…,M;j=1,2,3,…,N;

M——观测状态总数;

N——隐藏状态总数。

观测概率矩阵的定义考虑了时间t的因素,但在分析实际问题时做了简化,即在任何时刻,观测概率矩阵都不随时间变化,因此在理解观测概率矩阵时,可以把t去掉[2]。

通过观察海藻的湿度来确定隐含状态,定义海藻湿度为“dry(干燥)”“dryish(稍干)”“damp(微湿)”“soggy(潮湿)”4个等级。不同的天气状况下观测到的海藻湿度的概率是不同的,观测数据如表1所示。

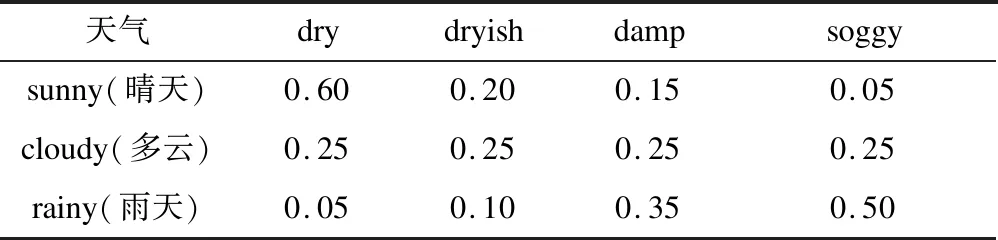
表1 不同天气状况下观测到的海藻湿度概率

1.2 观测概率矩阵

根据bj(k)的定义,表1所列出的概率其实就是观测概率矩阵。因此,bj(k)中的变量可以理解为:j表示不同的天气状态,k表示不同的海藻湿度等级。条件概率就是定义了在t时刻某个qj状态下,某个vk状态出现的概率。

由于观测概率矩阵不考虑时间因素,所以bj(k)也不会随着时间发生变化,写成矩阵的形式为

1.3 状态转换概率矩阵

隐马尔可夫模型中还定义了状态转换概率矩阵为

A=[aij]N×N

(2)

其中,aij=P(it+1=qj|it=qi)(i=1,2,3,…,N;j=1,2,3,…,N)是在时刻t处于状态qi的条件下,在时刻t+1转移到状态qj的概率。

马尔可夫链是随机变量X1,X2,X3,…,XN的一个数列。这些变量的范围,即它们所有可能取值的集合,被称为“状态空间”,而Xn的值则是在时间n的状态。如果Xn+1对于过去状态的条件概率分布仅是Xn的一个函数,则

P(Xn+1|X0,…,Xn)=P(Xn+1|Xn)·

P(Xn|Xn-1)…P(X1|X0)

(3)

该式在理论上是完美的,但在实际运用过程中存在两个问题:第一,假设要计算某个连续序列的概率,而这一概率会随着序列长度的增加不断减小,最后概率值将小到毫无意义;第二,每次计算都要记录前n次的状态,当序列长度增大时,数据量将明显增大,计算量也会变得相当大。因此,隐马尔可夫模型做了最基本的假设:当前状态只与前一个状态有关,即

P(Xn+1|X0,…,Xn)=P(Xn+1|Xn)

(4)

针对本文案例来说,今天的天气状态只受昨天天气状态的影响。但还需考虑时间段不同状态转移矩阵是否相同的问题。

按实际情况来说,万年前晴天转雨天的概率显然与如今晴天转雨天的概率是不同的,因此隐马尔可夫模型又做了一个不动性假设(状态概率转移矩阵与时间无关),即

P(Xi+1|Xi)=P(Xj+1|Xj),∀i,j

(5)

此处的i和j在海藻模型中分别表示地球时间第i天和第j天。

基于时间不动性假设,就可以统计状态转移的概率。假设历史上只出现了“sunny”“cloudy”“rainy”3种天气状态 ,那么就可以统计出某个时间段内,从一个状态转移至另一状态的频率(这里的频率可以理解为概率),如表2所示。

表2 状态转移概率

aij的定义正好与表2中从行到列的概率相对应。因此,状态转换概率矩阵为

1.4 初始状态概率矩阵

设置一个初始状态概率向量π为

π=(πi)i=1,2,3,…,N

(6)

其中,πi=P(i1=qi)是时刻t=1时状态qi出现的概率。

在海藻模型中,本文给出π=(0.6,0.2,0.2)。

1.5 隐马尔可夫模型的创建

一个完整的隐马尔可夫模型是由初始状态概率向量π、状态转移概率矩阵A和观测概率矩阵B所决定的,π和A决定状态序列,B决定观测序列。因此,隐马尔可夫模型λ可以用三元符号表示,即λ=(A,B,π),A,B,π称为隐马尔可夫模型的三要素。

隐马尔可夫模型是关于时序的概率模型,描述由一个隐藏的马尔可夫链随机生成不可观测的状态序列,再由各个状态生成一个观测结果而产生观测序列的过程。序列的每一个位置可以看作是一个时刻。

在海藻模型中,盲人每天第一件事情便是感知海藻的湿度,即每天记录海藻的状态。假设盲人连续记录了3天,海藻的观测序列为O=(dry,damp,soggy),则由隐马尔可夫模型可知,第1天海藻状态为dry,可能最佳隐藏状态为sunny;第2天海藻状态为damp,可能最佳隐藏状态为cloudy;第3天海藻状态为soggy可能最佳隐藏状态为rainy。由此得到天气的隐藏状态序列为I=(sunny,cloudy,rainy)。

2 隐马尔可夫模型的3个基本问题

2.1 概率计算问题

海藻模型中提出了在已知模型λ=(A,B,π)中求解P(O|λ)的问题。

在海藻模型中,根据观察序列寻找到一个隐藏序列,该概率可以表示为P(O|I,λ)。显然I序列的个数不只一个,3种天气状态对应3个序列,I的总数为3×3×3=27个,假设有N种状态,对应T个观察序列,那么I的总数为NT个。

将27个序列一一列举出来,分别进行计算。对固定的状态序列I={i1,i2,i3,…,iT},观测序列O={o1,o2,o3,…,oT}的概率为

P(O|I,λ)=bi1(o1)bi2(o2)·

bi3(o3)…biT(oT)

(7)

由于上述概率P(O|I,λ)是条件概率,即假定每个隐藏序列是已知的,故观测到的海藻状态与状态转移矩阵没有关系,只与其观测概率分布有关。如,已知3天的天气状态均为sunny,那么P(O={dry,damp,soggy}|I={sunny,sunny,sunny},λ)=b1(1)b1(3)b1(4)=0.60×0.15×0.05=0.004 5。

在状态转移矩阵中,只要知道初始状态概率向量π,就能够从某个时刻推断一连串隐藏状态序列的概率

P(I|λ)=πi1ai1i2ai2i3…aiT-1iT

(8)

式(8)对马尔可夫链的一阶假设进行了很好的简化。比如,第1天天气状态为sunny的概率为初始概率,已知;第2天为sunny的概率只与第1天的状态有关,也就是状态转移矩阵中sunny→sunny的概率;第3天仍为sunny的概率也只与前一天相关,即sunny→sunny的概率。因此,隐藏状态从一个状态转移至另一个状态,每次只要乘以状态转移矩阵中的某个值即可。

根据I出现的概率,以及在I出现的条件下O出现的概率,可以求得联合概率为

P(O,I|λ)=P(O|I,λ)P(I|λ)=

πibi1(o1)ai1i2bi2(o2)…aiT-1iTbiT(oT)

(9)

然后,对所有可能的状态序列I求和,得到观测序列O的概率P(O|λ),即

P(O|λ)=ΣIP(O|I,λ)P(I|λ)=

Σi1,i2…iTπibi1(o1)ai1i2bi2(o2)…

aiT-1iTbiT(oT)

(10)

上述算法不记忆先前的计算结果,算法传播到第3个状态后,一切推倒,重新计算。因此,这种算法在数据量大的情况下是不可行的。

在程序中有用空间换时间的思想,其实在数学公式中也是通用的。采用中间变量来记录结果,并利用该中间变量来计算后续节点,那么很明显可以极大地简化计算次数[3],减少计算量。

2.2 预测问题

根据给定的模型参数λ计算出P(O|λ)的值,给定一连串输入序列。对每个单词进行标注,从而使得整个隐藏序列对于观测序列来说概率最大[4],即P(I|O)最大。维特比算法是用动态规划解隐马尔可夫模型预测问题,即用动态规划求解概率最大路径(最优路径),这时一条路径对应着一个状态序列。

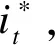
在t=1时刻,对于每一个状态i(i=1,2,3),求状态i下观测o1是sunny的概率δ1(i)为

δ1(i)=πibi(o1)=πibi(sunny),

i=1,2,3

(11)

代入实际数据后,可得δ1(1)=0.10,δ1(2)=0.16,δ1(3)=0.28。

对于t=1时刻,每个隐藏状态i可能出现sunny的概率与初始状态有关,与转移概率无关。在t=2时刻,对于不同的隐藏状态,有3条路径同时到达,此时不再计算3条路径的概率和,而是取其中概率最大的1条,代表从t时刻转移至t+1时刻,某一隐藏状态序列it,it+1出现ot,ot+1的概率最大。用公式表示为

(12)

计算可得:δ2(1)=0.028,δ2(2)=0.050 4,δ2(3)=0.042。同理,在t=3时刻,有

(13)

可得,δ3(1)=0.007 56,δ3(2)=0.010 08,δ3(3)=0.014 7。

用P*表示最优路径的概率,则

(14)

那么最优路径的终点

(15)

记录路径经过节点的变量定义为

i=1,2,3,…,N

(16)

3 结 语

隐马尔可夫模型参数的估计问题是一个隐藏变量的极大似然估计。对隐马尔可夫预测模型求偏导,得到极大似然函数的极值,再计算联合概率,而联合概率的计算巧妙地使用了节点图的各种性质,用中间变量降低了节点计算的复杂度,导出了对计算有帮助的定义,方便了参数求解。