多方控制的多粒子未知态双向量子隐形传态方案

曹海静, 范静怡, 曹 沐, 高俊杰, 夏明高, 王 骢

(1.上海电力大学 数理学院, 上海 200090; 2.中山大学 物理学院, 广东 广州 510275)

隐形传态是指某物在一处突然消失,同时在另一处突然出现的现象。简单地说,量子态携带的信息从一个地方移动到另一个地方,就是量子隐形传态,其安全性优于经典通信。这是由于量子的不可克隆定律和测不准原理,在传送过程中,一旦窃听者获取了量子信道传送的信息,则量子信道立即被破坏,窃听者仅仅通过经典方式无法复制量子态的信息,从而保证了信息传递的安全性。

自从1993年BENNETT C H等人[1]首次提出量子隐形传态方案后,人们开始对这种绝对安全的信息传递方式产生兴趣,从理论和实验两方面都进行了深入研究[2-16]。1998年,KALSSON A等人[2]提出了一种可控量子隐形传态方案,增加了第三方作为控制者,决定此次传态是否成功。CHEN Y[5]提出了基于五粒子纠缠态实现双向受控的量子隐形传态方案;YAN A[6]提出了利用六粒子Cluster态实现双向受控的量子隐形传态方案。其后,不同量子信道的双向受控量子隐形传态方案、双向非对称可控量子隐形传态方案[7-8]等相继被提出。2000年,LU H等人[9]和IKRAM M等人[10]分别提出了两粒子纠缠态的量子隐形传态方案。之后,三粒子GHZ态、三粒子W态的量子隐形传态方案[11-12]分别被提出,人们开始关注多粒子态的量子隐形传态方案。CAO Z L等人[13]和CAO M等人[14]提出了任意N粒子态的量子隐形传态方案,CHEN P X等人[15]提出了基于真实N粒子纠缠态信道的任意N粒子量子隐形传态方案。这些量子隐形传态方案逐步提高了信息传递的安全性和效率,同时也推动了量子通信和量子计算等领域的进步。

本文从最简单的单粒子未知量子态的隐形传态出发,再到两粒子的未知量子态,最后到多粒子的未知量子态,实现了多方控制的双向量子隐形传态。利用Bell态和GHZ态作为量子信道,采用Bell基测量和适当的单粒子幺正操作。方案操作简单,传输效率高,具有绝对的安全性。

1 两方控制的任意单粒子未知态双向隐形传态方案

文献[17]介绍了一种基于三粒子GHZ态的双向量子可控隐形传态方案,将一个控制者Charlie进行的粒子联合测量拆分为两个控制者Charlie和David进行的单粒子测量。

假设Alice要传送给Bob的粒子A,以及Bob要传送给Alice的粒子B的量子态分别为

|φ〉A=(A0|0〉+A1|1〉)A

(1)

|φ〉B=(B0|0〉+B1|1〉)B

(2)

其中,A0,A1,B0,B1为任意系数,满足|A0|2+|A1|2=1,|B0|2+|B1|2=1。

Alice,Bob,Charlie,David共享两个三粒子GHZ纠缠态作为量子信道,其形式为

(3)

(4)

其中,粒子1和粒子4属于Alice,粒子2和粒子5属于Bob,粒子3属于Charlie,粒子6属于David。

此时,量子系统的量子态为

(5)

4个Bell态分别为

(6)

首先,Alice对粒子A和粒子1、Bob对粒子B和粒子5做Bell测量,并将测量结果通过经典信道告知对方以及控制者Charlie和David。由于有4种不同的Bell基,测量后粒子A、粒子B、粒子3、粒子6的量子态塌缩为以下16种不同结果中的一种,且得到每种结果的概率相同。

式中,从左到右的符号“±”“+”分别表示Alice和Bob所做Bell测量的Bell基符号。

假如Alice和Bob的测量结果都是|φ+〉,则粒子2、粒子3、粒子4、粒子5的量子态塌缩为

|ψ〉2346=[A0B0|0000〉+A0B1|0011〉+

A1B0|1100〉+A1B1|1111〉]2346

(11)

Alice和Bob是否可以成功复制量子态和传递信息,取决于控制者Charlie和David是否同意。如果Charlie和David不希望传态继续,那么Alice和Bob仅根据对方的信息无法还原未知量子态,也就无法完成此次隐形传态。如果Charlie和David允许Alice和Bob继续传态,那么根据Alice和Bob的测量结果,Alice,Bob,Charlie,David分别对粒子2、粒子4、粒子3、粒子6进行相应的单粒子幺正变换,即I,σx,σy,σz。Alice的测量结果、Bob的幺正变换,以及控制者Charlie和David的幺正变换之间的对应关系如表1所示。

表1 Alice的测量结果及Bob和控制者的幺正变换操作

然后,Charlie和David分别对粒子3和粒子6进行H变换,H变换后粒子2、粒子3、粒子4、粒子6的量子态为

(12)

最后,Charlie和David分别对粒子3和粒子6进行单粒子态测量,并将测量结果通过经典信道告知Alice和Bob。Alice和Bob接收到所有信息后,分别对粒子4和粒子2进行相应的幺正变换(I或σz),即可还原对方的量子态,实现双向隐形传态。

2 两方控制的任意二粒子未知态双向隐形传态方案

假设Alice和Bob要向对方传送的二粒子态分别为

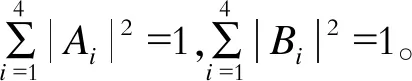
Alice,Bob,Charlie,David共享2个EPR对和2个四粒子GHZ纠缠态作为量子信道,其形式为

(15)

(16)

(17)

(18)

其中,粒子1、粒子3、粒子7、粒子9属于Alice,粒子2、粒子4、粒子8、粒子10属于Bob,粒子5和粒子11属于Charlie,粒子6和粒子12属于David。

此时,系统的状态为

(19)

Alice对粒子(a,1)和粒子(b,3),Bob对粒子(c,8)和粒子(d,10)分别进行Bell基测量,并将测量结果通过经典信道告知对方以及控制者Charlie和David。根据不同的测量结果,Alice对粒子7和粒子9,Bob对粒子2和粒子4进行相应的幺正变换,Charlie和David分别对粒子5、粒子6、粒子11、粒子12进行相应的单粒子幺正变换。测量结果与相应的幺正变换之间关系如表1所示。

然后,Charlie和David分别对粒子5、粒子6、粒子11、粒子12进行H变换和单粒子测量,并将测量结果通过经典信道告知Alice和Bob。Alice和Bob根据Charlie和David的测量结果,进行相应的幺正变换,就可以复制出Alice的未知态|φ〉A和Bob的未知态|φ〉B。

假设Alice和Bob进行的4组Bell基测量结果均为|φ+〉,则测量后粒子2、粒子4、粒子5、粒子6、粒子7、粒子9、粒子11、粒子12的量子态塌缩为

|ψs〉=a1〈φ+|b3〈φ+|c8〈φ+|d10〈φ+|ψ〉=

[(A1|00〉+A3|10〉)24⊗(|00〉)56+

(A2|01〉+A4|11〉)24⊗(|11〉)56]⊗

[(B1|00〉+B3|10〉)79⊗(|11〉)1112+

(B2|01〉+B4|11〉)79⊗(|11〉)1112]

(20)

根据测量结果可知,Alice和Bob对粒子7、粒子9、粒子2、粒子4,Charlie和David对粒子5、粒子6、粒子11、粒子12执行的幺正变换均相同。Charlie和David分别对粒子5、粒子6、粒子11、粒子12进行H变换后,量子系统的状态变化为

|ψ′s〉=H5H6H11H12|ψs〉=

[(A1|00〉+A2|01〉+A3|10〉+

A4|11〉)79⊗(|00〉+|11〉)511+

(A1|00〉-A2|01〉+A3|10〉-A4|11〉)79⊗

(|01〉+|10〉)511]⊗[(B1|00〉+B2|01〉+

B3|10〉+B4|11〉)24⊗(|00〉+|11〉)612+

(B1|00〉-B2|01〉+B3|10〉-B4|11〉)24⊗

(|01〉+|10〉)612]

(21)

Charlie和David分别对粒子5和粒子11、粒子6和粒子12进行单粒子态测量,并将测量结果通过经典信道告知Alice和Bob。当Charlie和David的测量结果为偶数个1(|00〉、|11〉)时,粒子7、粒子9和粒子2、粒子4的量子态为粒子a、粒子b、粒子c、粒子d的未知量子态,实现了信息的双向传递。当Charlie或David的测量结果为奇数个1(|01〉、|10〉)时,Alice或Bob需要对粒子7和粒子9或粒子2和粒子4进行σz幺正变换,才能复制出粒子a、粒子b、粒子c、粒子d的未知量子态,实现信息的双向传递。

3 M方控制的任意N粒子未知态双向隐形传态方案

假设Alice和Bob要向对方传送的任意N粒子态分别为

|φ〉X1X2…XN=(x1|0…00〉+

x2|0… 01〉+…+x2N|1…11〉)X1X2…XN

(22)

|φ〉Y1Y2…YN=(y1|0…00〉+

y2|0… 01〉+…+y2N|1…11〉)Y1Y2…YN

(23)

Alice,Bob和M个控制者(Charlie1,Charlie2,…,CharlieM)共享(2N-2)个EPR对|φ+〉DiBi(i=1,2,…,2N-2)和2个(M+2)粒子GHZ纠缠态作为量子信道,其形式为

(24)

|φ〉A2N-1B2N-1C1…CM=

(25)

|φ〉A2NB2ND1…DM=

(26)

其中,粒子(A1,A2,A3,…,A2N)属于Alice,粒子(B1,B2,B3,…,B2N)属于Bob,粒子(C1,C2,C3,…,CM)和粒子(D1,D2,D3,…,DM)分别属于M个控制者(Charlie1,Charlie2,…,CharlieM)。

此时,系统的状态为

(27)

Alice对粒子(Xi,Ai),Bob对粒子(Yi,Bi+N)(i=1,2,3,…,2N)分别进行Bell基测量,并将测量结果通过经典信道告知对方以及M个控制者。

根据不同的测量结果,Alice对粒子Ai+N,Bob对粒子Bi进行相应的幺正变换,M个控制者分别对粒子(C1,C2,C3,…,CM)和粒子(D1,D2,D3,…,DM)进行相应的单粒子幺正变换。测量结果和相应的幺正变换之间关系如表1所示。

由于有4种不同的Bell基,Alice和Bob共有4N种不同的测量结果。若Alice和Bob的测量结果均为|φ±〉,则在Alice,Bob,M个控制者进行相应的幺正变换操作之后,得到两种不同的测量结果为

(28)

式中,从左到右的“±”和“+”符号分别表示对粒子(Xi,Ai) (Yi,Bi+N)(i=1,2,3,…,2N)所做的Bell测量的Bell基符号。

M个控制者分别对粒子(C1,C2,C3,…,CM)和粒子(D1,D2,D3,…,DM)进行H变换,然后进行单粒子态测量,并将测量结果通过经典信道告知Alice和Bob。

H变换后的量子系统为

(29)

Alice和Bob根据M个控制者的测量结果,进行相应的幺正变换。

(1) 如果测量粒子(C1,C2,C3,…,CM)和粒子(D1,D2,D3,…,DM)的测量结果中均有偶数个1,则Bob的粒子(B1,B2,B3,…,BN)、Alice的粒子(AN+1,AN+2,AN+3,…,A2N)的状态就是任意N粒子态|φ〉X1X2…XN和|φ〉Y1Y2…YN的量子态。

(2) 如果测量粒子(C1,C2,C3,…,CM)或粒子(D1,D2,D3,…,DM)的测量结果中存在奇数个1,则需要Bob或Alice对粒子(B1,B2,B3,…,BN)或粒子(AN+1,AN+2,AN+3,…,A2N)进行σz幺正变换才能获得任意N粒子态|φ〉X1X2…XN和|φ〉Y1Y2…YN的量子态。

4 结 语

利用粒子的Bell纠缠态和GHZ纠缠态作为量子信道,通过Bell基联合测量和单粒子的幺正变换,实现了由多方控制的任意多粒子未知态的双向隐形传态。在本方案中,如果控制者希望这次隐形传态成功,则控制者需要选取合适的测量基对其拥有的粒子进行测量,并将结果通过经典信道告知接收方。控制者数量的增加有效地提高了通信过程的安全性。双向受控隐形传态可以实现信息的双向传输,提高量子态传输的效率。