基于ArcReLU激活函数的优化研究

徐菲菲, 许赟杰

(上海电力大学 计算机科学与技术学院, 上海 200090)

随着人工神经网络[1]的研究和发展,具有多层隐含层的深度学习逐渐成为人工智能领域中较为热门的研究方向,而伴随着神经网络的逐步发展,激活函数依旧是其结构中不可或缺的部分。若在神经元中不使用非线性的函数作为激活函数,那么无论神经网络具有多少隐含层,最终都只会得到输入数据的线性组合。这样的结果将会偏离现实情况,无法做到真正的拟合。因此,为了使神经网络可以应用于各种现实问题,需要引入非线性的因素。这是激活函数所具备的重要作用。本文将对各类不同系的激活函数进行研究和比对,综合其优点和不足之处,并加以改进,以达到提高收敛速度和计算精度的目标。

目前常用的激活函数大致分为Sigmoid系函数和线性整流函数(Rectified Linear Unit,ReLU)系函数两类。Sigmoid系中最具代表性的分别是Sigmoid[2]函数和Tanh[3]函数。这两个函数都具备可导性,但若输入值趋近于定义域边界时,其导数都将会趋于平缓,从而导致向下传播的梯度因子趋近零,最终会使神经网络参数难以得到有效的训练。上述情况就是Sigmoid系函数的软饱和性[4]所导致的梯度消失[5]现象。

为缓解梯度消失现象,研究者在Sigmoid系函数后提出了ReLU函数[6]。ReLU函数具有分段函数的结构特征,当输入值落入正半轴时,其导数部分恒为1,可以保持梯度在向下传播时不衰减,因此能够有效地缓解梯度消失现象。但是由于其负轴部分恒为零,因此负轴的导数部分将难以传递梯度变化,会产生神经元死亡现象。

指数化线性单元(Exponential Linear Unit,ELU)函数[3]作为ReLU函数的一种变体,可以较好地缓解神经元死亡现象。其负轴部分具备一定的软饱和性,整体而言更是解决了ReLU函数的均值偏移问题,是一个相对理想的激活函数。但由于其需要针对不同的模型修改参数,因此在实际应用中需要花费大量的成本进行训练和参数设置。

针对上述常见问题,本文对ArcReLU函数[7]进行了改进。实验结果表明:改进的ArcReLU函数具有更快的收敛速度,能够有效降低模型的训练误差,同时还能缓解梯度消失现象的发生;在解决ReLU函数神经元死亡问题的同时,由于其负轴部分的导数趋于零的速度更慢,相较于Sigmoid系函数更为缓和,学习效率也会得到进一步的提高;在为其添加了数超参数的改进后,使其增加了对数据集噪声的鲁棒性,缓解了均值偏移的问题。

1 线性整流函数和指数化线性单元函数

1.1 线性整流函数

ReLU函数可以有效地解决Sigmoid系函数引起的梯度消失现象。其定义为

f(x)=max(0,x)

(1)

其图像如图1所示。从图1不难看出,该函数负轴部分会出现神经元死亡的现象。

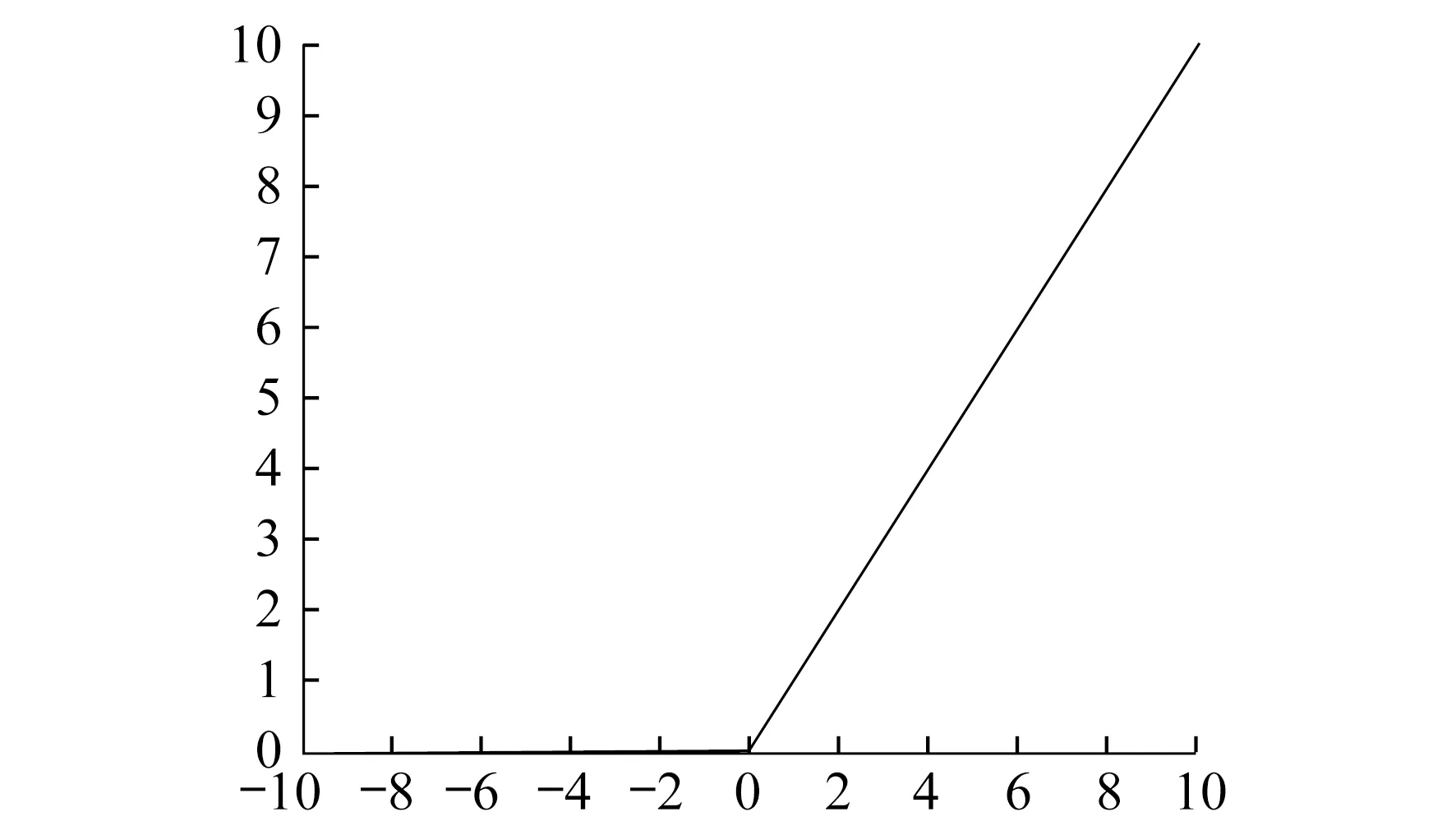
图1 ReLU 函数

从图1和式(1)可以看出:在正半轴其导数值恒为1,因此当输入值位于正轴时,能够保持向下的梯度不衰减,从而缓解梯度消失的问题;当输入值落入负半轴时,该函数具有硬饱和性[2]。若输入值位于负轴部分,神经元的梯度将难以保持传递,其权重值也将无法更新,进而导致计算结果无法收敛。整体而言,ReLU函数虽为分段函数,但其输出均值恒大于等于零,即存在均值偏移问题[8]。这将会使神经网络具备稀疏特性。

1.2 指数化线性单元函数

ELU函数是对ReLU函数的一个改进,其定义为

(2)

其图像如图2所示。

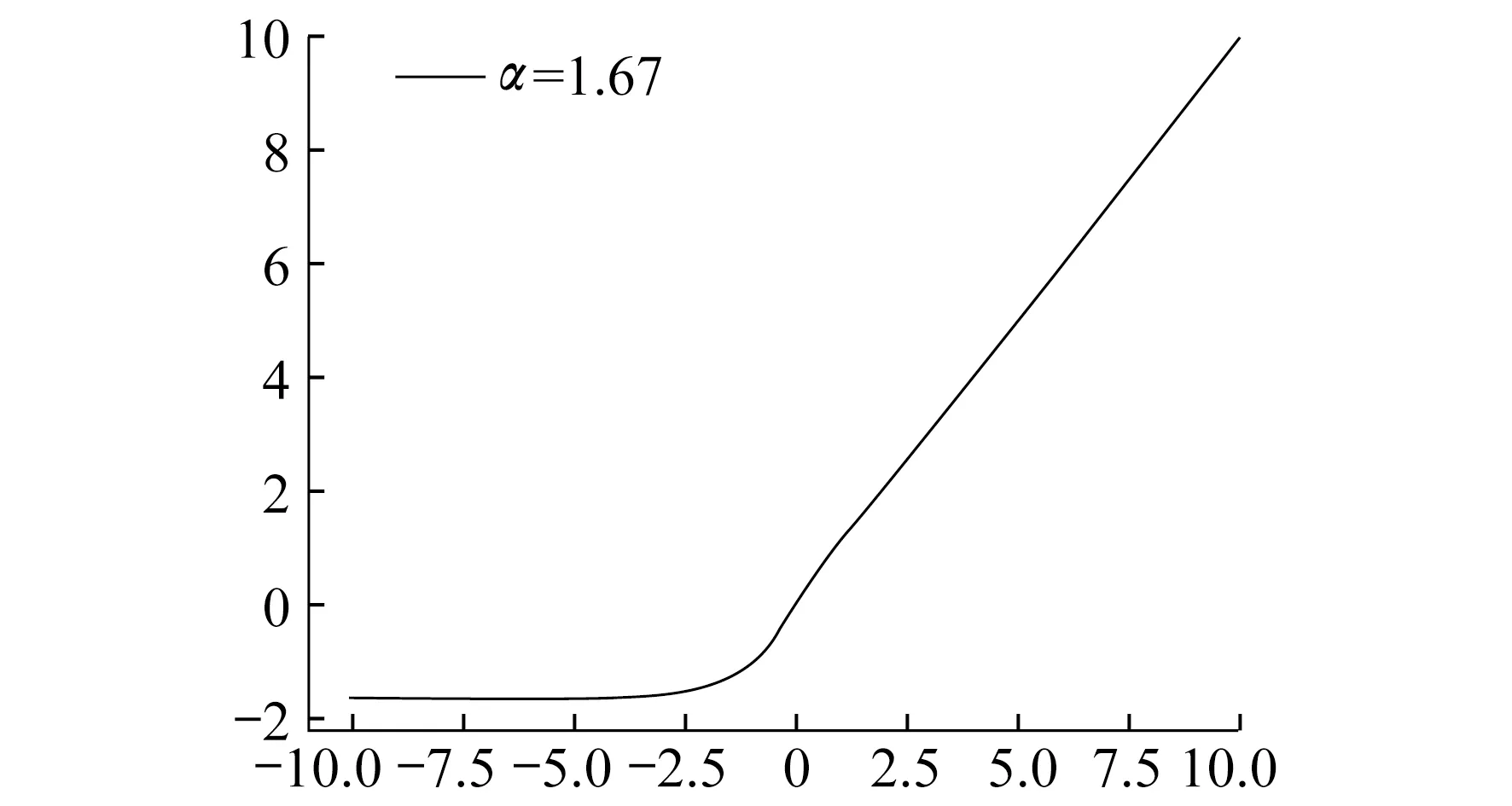
图2 ELU函数

从式(2)和图2可以看出,ELU函数在正半轴可以有效地缓解梯度消失现象,而负半轴部分能够让ELU函数对输入值的变化具有更好的鲁棒性。整体而言,ELU函数的输出均值趋近于零,因此具有更快的收敛速度。

2 ArcReLU函数的优化

2.1 ArcReLU函数

(3)

其函数图像如图3所示。

图3 ArcReLU 函数

依据图3提出初步假设,该函数在其定义域范围内连续且单调递增。为证明上述理论,需要先验证该函数在原点处的可导性。将正轴部分定义为f1(x),负轴部分定义为f2(x),证明如下。

f(x)=f(x-)=f(x+)=0,x=0

(4)

(5)

(6)

依据式(4)可得ArcReLU函数在原点处有定义且连续。因为式(5)与式(6)存在结果且相等,依据导数定义,该函数在原点处连续且可导,因此该函数可用于反向传播帮助算法沿负梯度方向调整参数,并可得出ArcReLU的导数为

(7)

从式(7)可得,ArcReLU函数的导函数值恒大于零。依据导数定义,可证明其为单调递增函数。当激活函数具备单调性时,单层网络能够保证为凸函数[9],从而可推断出该函数在训练过程中将具有更好的收敛性。

2.2 RArcReLU函数

为提高ArcReLU函数的收敛速度,并使其具备更好的鲁棒性,本文对其作进一步的改进。将改进的ArcReLU函数称为RArc-ReLU函数,其定义为

(8)

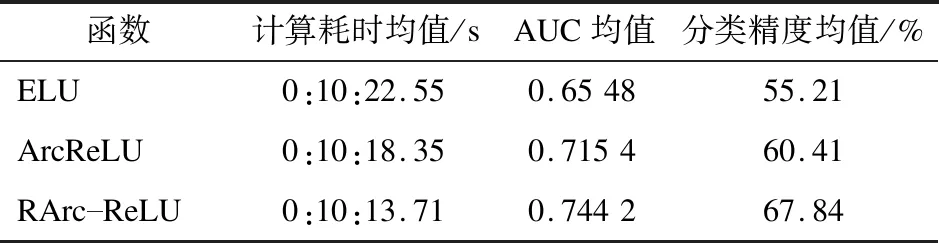
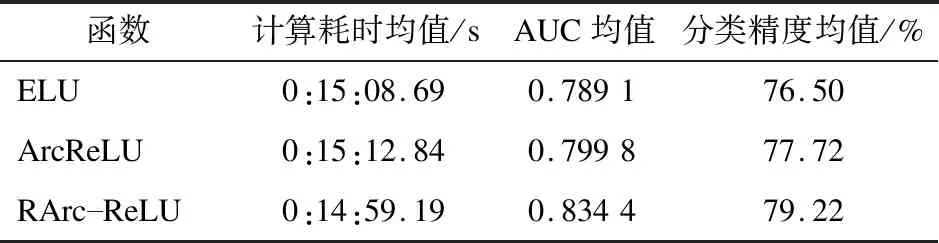
其中,λ为一个从均匀分布的G(i,j)中随机抽取的数值,λ∈G(i,j),i

式(8)中,为ArcReLU的负轴部分添加了一个非线性因子1/λ。从式(8)不难看出,当λ取值为1时,新的函数将会退化为ArcReLU函数;当λ取值为零时,新的函数将会退化为ReLU函数。

因此,为避免上述退化情况的出现,λ的取值范围将定义为[0,1),实际训练过程中会采用所有λ的均值构建非线性因子,使函数整体具有更好的自归一化作用和更好的拟合能力。另外,优化函数后,将使函数的负半轴更为缓和,能够更有效地缓解梯度消失的问题。

3 实验与结果分析

3.1 实验数据

本文在BP神经网络中使用UCI上的公开数据集,分别对ELU函数、ArcReLU函数和RArc-ReLU函数进行4次对比实验。实验在Windows 10操作系统下,通过Python3.7.2编写程序进行。4组数据集分别为:关于皮马印第安人糖尿病情况的数据统计,数据集共768个对象;汽车评估数据集,共1 728个对象;美国人口普查收入情况统计,数据集共9 502个对象;阿维拉数据集,共12 647个对象。4组数据集中所包含的属性分别如表1～表4所示。实验中,将各表中最后一个属性作为决策属性,取值均做量化处理。

表1 关于皮马印第安人糖尿病情况的数据统计

表2 汽车评估数据集

表3 美国人口普查收入情况统计

表4 阿维拉数据集

本次实验将在2层BP神经网络[8]中,使用10次十折交叉验证法进行测试。通过在4组不同的数据集上对3种激活函数进行对比实验,能够直观地得出各激活函数的优点与不足。实验中,学习率η经过多次实验取值为0.001,迭代次数设置为5 000次,λ取值范围为[0,1)。

鉴于数据集中各属性具有不同的量纲方式,会影响对最终数据结果的分析,因此为减少指标间的量纲影响,本文在实验前采用Z-score标准化的方式对数据集进行了预处理,以确保在不消除指标特征性的同时使其维持在相同的范围内。

3.2 各数据集实验结果对比

4组数据集的实验结果对比如表5～表8所示。

表5 皮马印第安人糖尿病数据集实验结果对比

表6 汽车评估数据集实验结果对比

表7 美国人口普查收入实验结果对比

表8 阿维拉数据集实验结果对比

由上述4组实验结果可知,RArc-ReLU的计算时间均少于ArcReLU和ELU两个函数,其收敛速度和分类精度在实验中均高于另外两种激活函数。

4 结 语

本文通过分析和研究常用的经典激活函数,对新构造的ArcReLU函数进行了进一步的改进,提出了RArc-ReLU函数,从而在保持原有优点的情况下,提高了其收敛速度和分类精度。通过4组不同的数据集,对ELU函数、ArcReLU函数和RArc-ReLU函数进行了对比实验。结果表明,RArc-ReLU函数初始的累积误差小,因此达到收敛值所需的时间会较少。伴随神经网络不断的迭代,RArc-ReLU函数将更快趋于平稳,说明其相较于另外两种函数具有更好的收敛性。在分类精度上,该函数能够有效地降低训练误差,同时能够有效缓解梯度消失和神经元死亡的问题。实验中RArc-ReLU的AUC值相较于另外两种激活函数都大,由此可见,RArc-ReLU具有更佳的泛化性能。

此外,由于在RArc-ReLU函数中添加了非线性因子,使其能够帮助模型更好地拟合不同的数据集。RArc-ReLU在计算速度上也有所提高,相较于改进前的ArcReLU函数在计算消耗上更快且更为平稳。下一步的研究工作将针对RArc-ReLU是否能够提高深度学习模型的计算速度和精准度进行探索。另外,还将尝试使用更多种类的数据集对RArc-ReLU函数的鲁棒性进行研究。