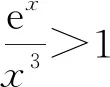基于学生思维 解决学生问题
王弟成
(江苏省苏州实验中学 215011)
提高高三数学复习效益,提高学生数学综合能力,提升学生核心素养,让学生获得高考理想成绩,是高三教学的重要目标.高三教学中我们始终坚持“基于学生思维,解决学生问题”的教学方法,让学生思维先行,展示学生思维,学在教的前头,教师针对学生“已有思维”及时诊断,发现问题,引导学生质疑探究,激发学生思维,比较改进,优化提升.在解决学生问题过程中落实四基,发展四能,提升素养,取得较好的复习效果.现以一道高考函数综合题求解教学为例,谈谈我们的教学思考.
题目:(2018全国卷Ⅱ)已知函数f(x)=ex-ax2.
(1)若a=1,证明:当x≥0时,f(x)≥1;
(2)在(0,+∞)只有一个零点,求a.
第(1)问给出a=1,f(x)是具体函数,学生按步骤有序思维,连续求导,判断单调区间,求最小值,再判断单调性,寻求最小值.难度不大,学生不存在问题,都能正确解答.
学生解答主要是第(2)问不会解、不严谨、不全面,所以课堂教学主要针对(2)问教学.
1 展示解法 指出问题 探究完善
学生解法1由f(x)=ex-ax2,得f′(x)=ex-2ax,
设g(x)=ex-2ax,则g′(x)=ex-2a.
(i)当a≤0时,g′(x)=ex-2a>0,
所以g(x)=ex-2ax在(0,+∞)上单调递增,
又g(0)=1,所以g(x)>g(0)=1>0,
所以f(x)在(0,+∞)上单调递增,
所以f(x)>f(0)=1>0,
所以f(x)在(0,+∞)上没有零点.
(ii)当a>0时,由g′(x)=ex-2a>0得,
当x∈(-∞,ln 2a)时,g(x)单调递减,
当x∈(ln 2a,+∞)时,g(x)单调递增.
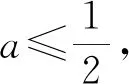

所以在(0,+∞)上,g(x)有最小值,即
g(x)min=g(ln 2a)=2a-2aln 2a
=2a(1-ln 2a), ……
教学片断1: 改进讨论过程 优化讨论切入点
师:上面是部分同学的解法,主要是从参数a的一般情况讨论起,分a≤0,a>0等情况讨论,同学们考虑是否可以改进?
生2提出,讨论可以改进,由于当x≥0,此时ex≥1,所以可以直接讨论2a与1的关系.

学生解法2由f(x)=ex-ax2,
得f′(x)=ex-2ax,
设g(x)=ex-2ax,则g′(x)=ex-2a.
由于x∈(0,+∞),所以g(x)=ex>1.
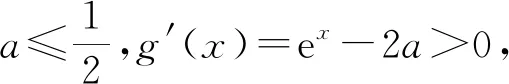

g(x)min=g(ln 2a)=2a-2aln 2a
=2a(1-ln 2a),
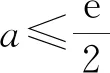
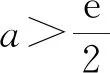
教学片断2: 点出关键问题 师生探究完善
学生一片沉默,没有提出异议,显然认为这样解答可以了.这样老师先指出问题所在,以启发学生思考.
经老师提醒生3提出要说明g(x)是否有零点,仅有单调性是不够的.由于当x∈(0,ln 2a)时,由于g(0)=1,g(ln 2a)<0,g(x)是连续的,必存在x1∈(0,ln 2a)使g(x1)=0.所以g(x)一定是先正,后负,再正,因为g(x)一定有零点.
师:很好!找到这个x1是必须的,那(ln 2a,+∞)呢?要不要也说明g(x)有零点呢?否则g(x)单调递增是下列哪种情况呢?同学们为什么自觉认为是第二种情况,理由是什么?
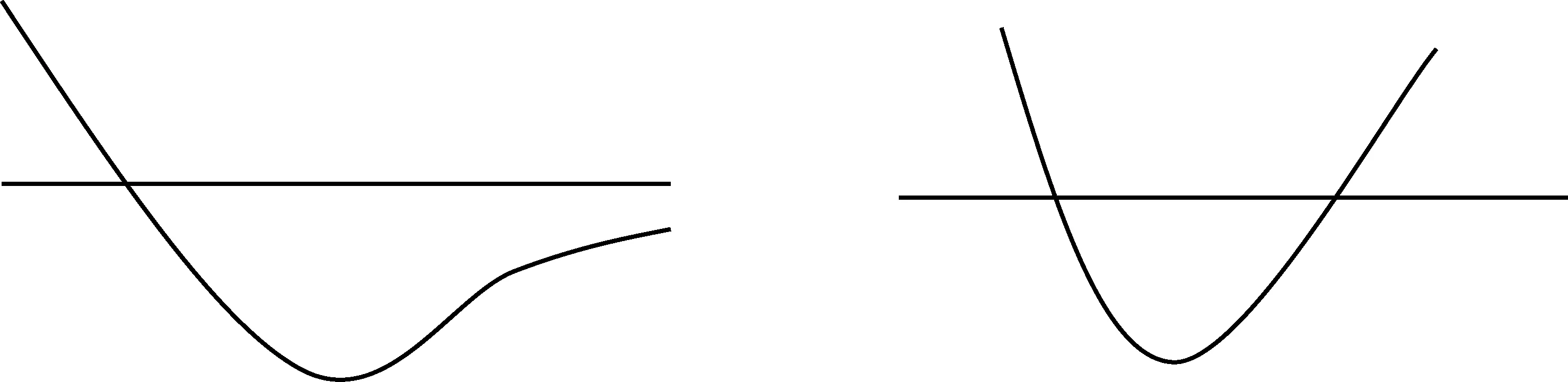
学生4提出从直观感知,g(x)的图象应是第二种情况,但直观不能代替推理,还是要在(ln 2a,+∞)找x2使g(x2)=0,但学生普遍感到困难无多下手。
师:(1)问所证明结论ex-x2≥1能给我们什么启发?此式能说明什么问题?
在教师启发后,生5提出可以借助不等式ex-x2≥1进行放缩.由ex-x2≥1,得ex≥x2+1,所以ex>x2.所以当x∈(0,+∞)时,易证2a>ln 2a,所以g(2a)=e2a-2a·2a>(2a)2-4a2=0,所以在(ln 2a,+∞)上存在x2=2a使g(x2)=0.所以g(x)在(0,x1)为正,在(x1,x2)为负,在(x2,+∞)为正,从而f(x)先增,后减,再增.
师:同学们补充得非常好.通过第(1)问隐含的信息,结合放缩统一ex与x2关系,其目的是为方便找到x2,这也是这类问题中找点常用手法,希望同学们能够理解、掌握,并学会迁移运用.至此解法2是否就完善了?
生5提出对于f(x)也存在同样的问题,要说明是否存在零点,否则也是不完善的,也会出现如图所示情况.
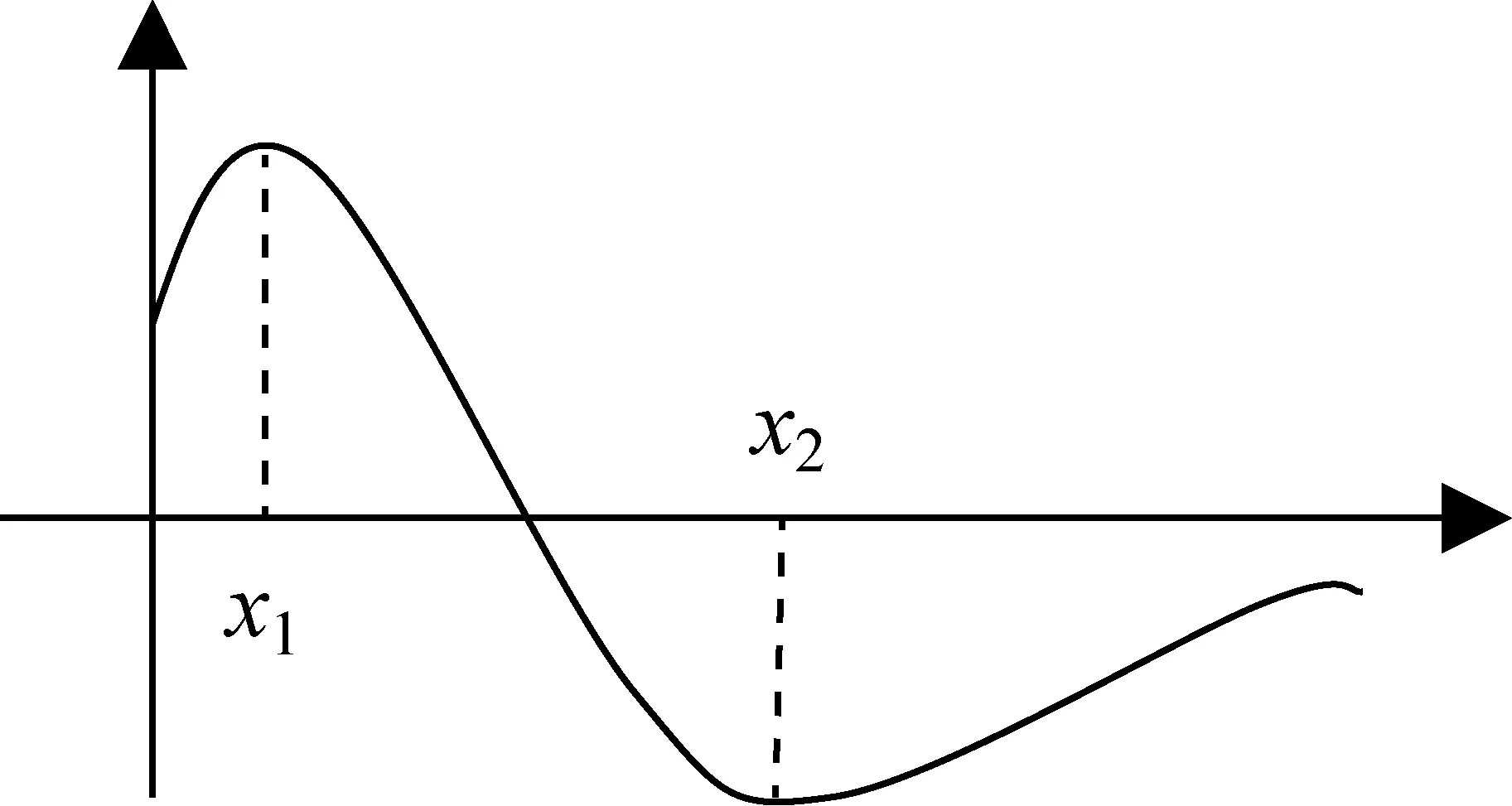
由于f(0)=1>0,所以f(x1)>1,
而g(x2)=ex2-2ax2=0,

若x2<2,则f(x2)>0,此时f(x)没有零点.

生6提出由(1)得x>0时,ex>x2,若直接放缩得f(x)>x2-ax2,又x2-ax2<0,不可能成功.
师:为什么会是这样?说明什么问题?大家可以直观感觉到当x→+∞时,f(x)>0.怎么办?画画图象看能给我们什么启发?
生7提出可以将ex放大一点,考虑证明ex>x3.
师:如何证明?请大家动手.
设h(x)=ex-x3,(x>0),证明h(x)>0.要进行三次导,很麻烦.
师:好!上面证明ex>x3,处理方法很值得我们借鉴.积式比差式好,积式求导后方便求出单调区间.还能放再大一点吗?如能证明ex>x4(在一定区间上)也行,ex>x2对我们有什么启发?如令x=2a,则有e2a>(2a)2=4a2,也可以变为e2a=(ea)2>(a2)2=a4等等,如何选择x的值,能使f(x)>0?
生9提出选择x=4a,f(4a)=e4a-a(4a)2=(e2a)2-a(4a)2>16a4-16a3>0.
师:漂亮!利用已证明结论,作适当变换,就得到所要的结果,这是最经济的事.这也是我们解题要特别注意的地方.至此我们完整地、严谨地解决此题.虽然讨论有点烦,但我们解决了,我们成功了,收获很大.下面看解法3.
教学片断3: 类比思维 发现问题 自我解决

师:这是部分同学的解法,很漂亮.繁则思变,对给定的函数通过函数与方程关系进行等价转换,把所求参数分离出来,构造出无参数函数,寻求不一样的解法,其思路明显比解法1简捷!讨论减少了,为什么会出现简捷情况?
生10认为通过分参后使所求解函数中不含有参数,函数是具体的,图象是固定的,单调性是定的,不需要对参数a分类讨论,当然简捷.
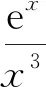

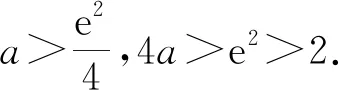
2 比较改进 优化提升
教学片断4:比较解法2与3,形成新方法
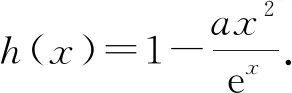
(i)当a≤0时,h(x)>0,h(x)没有零点;
(ii)当a>0时,h′(x)=ax(x-2)e-x.
当a∈(0,2)时,h′(x)<0;
当x∈(2,+∞)时,h′(x)>0.
所以h(x)在(0,2)单调递减,在(2,+∞)单调递增.
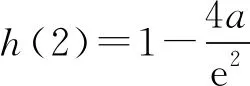
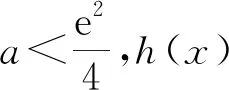

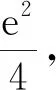
所以h(x)在(0,2)有一个零点,
由(1)知,当x>0时,ex>x2,
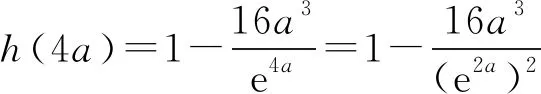
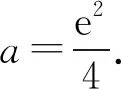
此题看答案似乎很简洁,但简洁却不简单,简洁中却蕴含不简单的思维,不简单的方法,不简单思想,需要在不同解法中比较感悟,细节问题不同处理中,才能感得真谛!
3 反思感悟 改进坚持
(1)高三教学要让学生思维先行
让学生的思维走在教师的前头.高三复习不是知识、方法、思想的简单重复,更不是概念、性质、公式的简单回忆,而是学生在学习内容丰富后对知识、方法、思想的再认识,再理解.从系统的视角,联系的观点,整体的认识,对知识理解的再深化.所以高三教学是让学生建构更深层的理解,更高阶的思维,更综合的能力,更核心的素养.但高三又是学生学习后的再学习,学生已掌握基础知识、基本方法,积累了大量的数学基本活动经验,所以教学又不能同于新授课教学,学生具备先解决条件.我们复习指导原则是“基于学生思维,解决学生问题”.让学生思维先行,思在讲的前头,行在教的前面.教师有针对性地点拨、讲解,引导学生质疑探究,合作学习,从而提升能力,提高素养.
知识让学生梳理,学生自己看教材,根据一节或一单元内容自己系统梳理知识,包括概念、性质、定理等.学完一个单元后,再根据复习补充的内容进一步完善知识系统,形成有联系的知识“群”.练习让学生先做,根据课堂时间让学生课前先做一部分习题,即使课堂上补充的例习题,也要让学生先做,做后再讲,不做不讲.想法让学生先说,习题的解法、思路要让学生先说,教师针对学生思路,或启发思考,或点拨讲解,或引导探究,或总结完善.错误让学生先犯,学生有错误是正常的,有的错误也是老师防不住的,有问题先让学生暴露,在错误基础上讲解才能理解更深刻.如本节课学生解法都有问题,让学生暴露错误后再针对性探究讲解,效果更好.反思让学生先来,学习离不开反思,知识的深度理解,方法的准确运用,思路的灵活转换,思想的自觉引领,能力的提升,素养的达成,都离不开学生的自我反思,在反思中提升.总之教师要鼓励学生先行,做“解题方法的创造者,而不是习题答案的搬运工”.
(2)高三教学要基于各种资源重新设计课堂教学
教师的经验,资料的习题,学生的解答等等,都是课堂教学的资源,课前教师收集整理各种资源,课堂要基于各种资源重新设计课堂教学.本题是一道高考题,练习中全班无一位同学解答与参考答案相同,说明学生都想不到这样解,当然与之前未系统讲解过此类题也有一定关系,但参考答案思想方法又必须让学生深刻理解,所以借此题详细讲解,讲深讲透此类问题的处理方法与技巧很有必要.参考答案的方法是最简捷的解法,很多简捷的思维蕴含其中,课堂若直接呈现给学生,告诉学生,学生能接受、理解,甚至能模仿,但未必能理解其中的深意,不理解的方法是不可能迁移到新情境中的,自然谈不上灵活运用.学生的解答多集中在解法1与解法2,而这两种解法放在一起比较,集中不同优点,正好形成参考答案的解法.所以课堂教学看似无意,讲解学生的解法,实则有意设计,基于学生的解法1与解法2,在比较基础上提出解法3,学生理解自然水到渠成,甚至解法3学生都自己能创造出来.这样方法不是老师强行“介绍”的,是学生在深刻理解基础上自然形成的,学生既会,也懂,能用.既学会方法,也提升能力.这就需要教师根据各种资源灵活设计.
(3)高三教学要完善、提升学生解法,发展学生思维