选择决策游戏与贝叶斯公式

李增沪

(北京师范大学数学科学学院 100875)

1 选择决策游戏

有个请嘉宾选择奖品的游戏，主办方在编号为1,2,3的三个门中等可能地随机选择一个，放入一辆跑车，另两个门里各放一只山羊．节目的嘉宾不知道哪个门里是跑车．主持人请嘉宾选择一个门，门后的奖品由他获得．嘉宾希望选中跑车.

假设你是嘉宾，选择了1号门，在此门打开之前，主持人打开了余下的门中的一个，显示里面是山羊，不妨假设他打开的是3号门．现在主持人给了你重新选择的机会，你是坚持选1号门？还是改选2号门？

这个游戏来源于一个著名的电视节目，曾经引起广泛关注和讨论．下面针对两种不同的游戏规则，在高中数学知识水平上，分别给出上面问题的分析．

规则1主持人知道跑车在哪个门里．在嘉宾初次选择后，他只打开余下的门中有山羊的门．

规则2主持人不知道跑车在哪个门里．在嘉宾初次选择后，他在余下的两个门中等可能地随机打开一个．

同理有

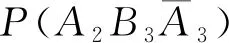
根据条件概率的定义得

对于上面讨论的选择游戏的各种推广及有关该问题的细致讨论，可以参阅[3,4,5]以及那里所列举的参考文献．

2 基于贝叶斯公式的分析

贝叶斯公式的思想最早出现于贝叶斯的论文[1]，发表于他去世后的1763年．后来拉普拉斯[2]独立地发现了这个公式，此后其意义逐渐被人们理解和重视．统计学家经过长期的努力，发展出了以贝叶斯公式为基础的系统的推理和决策方法，称为贝叶斯方法．该方法的基本程序是首先根据实际情况确定先验概率，然后利用贝叶斯公式计算得到后验概率，对先验概率进行修正和校对，再根据后验概率做出推理和决策．

贝叶斯公式(Bayes formula)：设A1,A2,…,An是两两相斥的事件组，满足P(Ai)>0,i=1,2,…,n且A1∪A2∪…∪An=Ω．对任意事件B⊆Ω,P(B)>0，有

考虑按照规则1设计的选择决策游戏．为了简单起见，下面假定当主持人有两个有山羊的门可以打开时，他等可能地随机选择其中一个打开．在这种情况下，应用贝叶斯公式，可以从条件概率的角度，给出上述决策问题的另外一个分析和解答．

(2)跑车在2号门里，主持人只有3号一个门可以打开，故P(B3|A2)=1；

(3)跑车在3号门里，主持人只有2号一个门可以打开，故P(B3|A3)=0．

利用全概率公式，主持人打开3号门的概率为

再根据贝叶斯公式，在3号门打开的条件下，1号和2号门里有跑车的概率分别为

这两个条件概率是后验概率，它们利用主持人打开有山羊的3号门这个信息，修正了前面的先验概率．通过比较后验概率发现，在规则1之下，改选2号门是正确的决策．

3 多次选择游戏

考虑多个门的选择决策游戏．假设主持人事先在编号为1,…,n的n(n≥3)个门中选择了一个，里面放入一辆跑车，而其他每个门里各放一只山羊．嘉宾不知道哪个门里是跑车．游戏规则是嘉宾选择一个门，这个门里的奖品由他获得，嘉宾希望选中跑车．假定嘉宾选择了k号门，在此门打开之前，主持人在余下的有羊的门中等可能地随机选择了一个并打开，不妨设打开的为m(m≠k)号门．接着主持人给了嘉宾一次重新选择的机会．试问嘉宾能否通过改变选择，提高成功获得跑车的概率？

命题1用Ai表示i号门里是车，Bi表示主持人打开i号门．假设i号门里是车的概率为P(Ai)=pi(1≤i≤n)．那么在m号门打开的条件下，k和i(i≠k,m)号门里有车的概率分别为

证明考虑到嘉宾已经选k号门这个事实，根据游戏规则，在k号门里是车的条件下有

而在i(i≠k)号门里是车的条件下有

P(Bi|Ai)=P(Bk|Ai)=0,

利用全概率公式，主持人打开m(m≠k)号门的概率为

根据贝叶斯公式，在m号门被打开的条件下，k和i(i≠m,k)号门里有车的概率分别为

和

令c=(n-2)P(Bm)即得命题的结论．

其中为公共常数．这是嘉宾和主持人第1次互动的后验概率，也是他们第2次互动的先验概率．再次应用命题1我们发现，去掉打开的m1,m2号门，有车的概率在剩下的n-2个门里分别为

和

其中c1和c2均为公共常数．这是嘉宾和主持人第2次互动的后验概率．不难发现

P(Ak2|Bm2)

所以嘉宾应该改变自己的选择，在k1和k2号之外另选一个门以获得最大的成功概率．

继续上面的游戏，假设在嘉宾每次选择一个门之后，主持人总是随机打开余下的一个有羊的门，并给嘉宾一次重新选择的机会，直到剩下最后两个门为止．试问嘉宾应该怎样决策，才能保证每一步都以最大的概率选中跑车？

分析5根据前面的讨论，可以归纳出嘉宾应该遵循的原则：(1) 每次得到重新选择的机会时，都改变自己的选择；(2) 重新选择的时候，首先选择此前没有被选过或者被选中次数最少的门；(3) 在此前被选次数相同的门中，选择之前被选中最早的门．

在关于多次选择游戏的讨论中，反复应用了贝叶斯公式，而且这种方法具有一般性．在游戏中，主持人每打开一个门都提供了有用的信息，嘉宾需要不断根据这些信息，利用贝叶斯公式计算出剩余的门里有跑车的后验(新的)概率分布，并据此修正自己的选择以增加获得跑车的概率．这种不断改进和校正决策的过程非常近似于人类的学习和思维模式，也是贝叶斯方法许多应用的关键.例如著名的围棋人工智能系统阿尔法狗(AlphaGo)系统就使用了这样的想法.现在正是由于这个特点，贝叶斯方法在人工智能领域发挥了非常重要的作用，已经成为学习型人工智能的理论基础．

注：本文可作为现行普通高中数学教材中贝叶斯公式部分的扩展阅读材料.