一类含参广义混合拟向量均衡问题解的Hölder连续性与上估计

宋建成

(西南民族大学 数学学院，四川 成都 610041)

1 引言及预备知识

向量均衡问题是运筹学中一类重要的优化模型，近几十年大量优化学者对其进行了研究.其研究对象包含向量优化问题、向量互补问题、向量Nash平衡等问题解的存在性及稳定性.目前，大量学者已讨论了众多向量均衡问题解的存在性，见文献[1-2]及其参考文献.解的稳定性分析，或灵敏度分析，同样是向量均衡理论研究的重要课题，主要研究各类连续性，如Lipschitz连续及Hölder连续等.Chen等[3]研究了含参广义向量均衡问题解映射的下半连续性.陈和龚[4]在拓扑向量空间中，运用标量化方法给出了含参集值弱向量均衡问题解集映射连续性的充分性条件.Shan等[5]研究了含参广义向量拟均衡问题解的上半 连 续 性.Anh和Khanh[6]、Li等[7-8]、Chen等[9-10]等和Ji[11]分别考虑了几类广义向量拟均衡的解的Hölder连续.其中，Ji[11]讨论了对参数为θ∈T，μ∈W的如下含参广义混合拟向量均衡问题:

其中X、T及W均为距离空间，Y定义为线性距离空间，K⊂Y是给定的非空闭凸锥，且intK≠∅.d(·，·)定义为距离空间中的度量.设K:X×T→2X，φ:X×X×W→2Y，ψ:X×W→2Y是三个非空集值映射.本文作为文献[11]的后续工作，继续研究含参广义混合拟向量均衡问题解的Hölder连续性.余下部分将考虑对参数为θ∈Λ，μ∈W的含参广义混合拟向量均衡问题:求，使得

构造F(x，y，μ)=φ(x，y，μ)+ψ(y，μ)-ψ(x，μ)，E(θ)={x∈X|x∈U(x，θ)}，∀(θ，μ)∈T×W.记(QVEP)的解集为S(θ，μ)，即

我们注意到若ψ(x，μ)=ψ(μ)，U(x，θ)=U(θ)，那么问题(QVEP)就退化为一般的含参广义向量均衡问题，也可表示为，使得，μ)⊂Y＼-intK，∀y∈U(θ).此问题由S.J.Li在文献[8]作了研究.对，设的邻域为.我们假设对×.下面介绍本文需要的相关定义.

定义1[12]集值映射L:T→2X在μ0被称为l.α-Hölder连续的，如果有λ0的邻域N(λ0)使得

∀λ1λ2∈N(λ0)，L(λ1)⊂L(λ2)+lB(0，dα(λ1，λ2))，其中l≥0且α＞0.

定义2[12]集值映射L:X×Λ→2X在(x0，θ0)被称为(l1.α1，l2.α2)-Hölder连续的，如果存在x0的邻域N(x0)及θ0的邻域N(θ0)使得对∀x1，x2∈N(x0)，∀θ1，θ2∈N(θ0)，有

L(x1，θ1)⊂{x∈X|∃z∈L(x2，θ2)，d(x，z)≤，其中l1，l2≥0且α1，α2＞0.

定义3[13]设(Θ，d)是距离空间，Π(Θ)为该空间上所有非空有界闭子集所形成的集簇.

H(X，Y)=max{supx∈Xd(x，Y)，supy∈Yd(X，y)}，∀X，Y∈Π(Θ)，

其 中d(x，Y)=infy∈Yd(x，y)，d(X，y)=infx∈Xd(x，y).则H被称为Θ上集簇Π(Θ)的Hausdorff度量.

2 主要结论

在这一节我们给出问题(QVEP)的解集的Hölder连续性和上估计.

定理1假设在的邻域内(QVEP)问题的解存在，进一步假设如下的条件成立:

②对每一(θ，μ)∈，在E(θ)×K(E(θ)，θ)内，φ(·，·，μ)是具紧值下半连续的，ψ(·，μ)在U(E(θ)，θ)内是具紧值连续的；

则对任何(θ，μ)∈，S(θ，μ)是E(θ)的紧子集.

证明由于E(θ)是紧的，只需刻画在E(θ)中S(θ，μ)是闭的.取任何序列{xn}⊂S(θ，μ)，xn→x0，由于xn∈E(θ)及E(θ)的紧性，则有x0∈E(θ).事实上，我们假设x0∉S(θ，μ)，则∃y0∈U(x0，θ)，使得z0∈F(x0，y0，μ)∩(-intK).

因为U(·，θ)在x0是下半连续的，对y0及{xn}，存在yn∈U(xn，θ)使得yn→y0.φ(·，·，μ)是具紧值上半连续及ψ(·，μ)是具紧值连续的，则对z0∈F(x0，y0，μ)，存在zn∈F(xn，yn，μ)∩(Y＼-intK)使得zn→z0.当n足够大时，zn∈-intK.由于xn∈S2(θ，μ)，有zn∈F(xn，yn，μ)⊂Y＼-intK，这与zn∈-intK矛盾.因此x0∈S2(θ，μ)，即S(θ，μ)是闭的，该命题得证.

定理2假设在内，(QVEP)问题的解存在并且满足定理1的条件，并且进一步假设如下的条件成立:

①U(·，·)在内是(l1.α1，l2.α2)-Hölder连续的；

③∀(λ，μ)∈，∀x∈E(λ)，F(x，·，μ)在是n.δ-Hölder连续的；

④存在常数α＞0，β＞0，使得∀(θ，μ)∈，∀y∈Δ2(θ，μ):=)＼S(θ，μ)，∈S(θ，μ)满足；

⑤β=α1δ，α＞.

进一步假设β＞θ.则S(·，·)满足Hölder连续的条件，即∀(θ1，μ1)、(θ2，μ2)∈，有

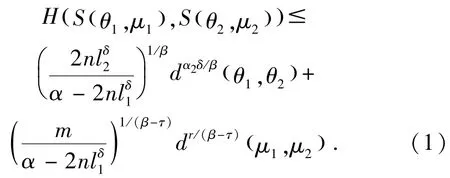
证明由定理1可知，对任何×，S(θ，μ)是E(θ)的紧子集.如果S(θ1，μ2)≠S(θ2，μ2)，且S(θ1，μ2)⊄S(θ2，μ2)与S(θ2，μ2)⊄S(θ1，μ2).那么对所有x(θ2，μ2)∈S(θ2，μ2)＼S(θ1，μ2)，我们由(4)的假设可得使得

由于U(·，·)是(l1.α1，l2.α2)-Hölder连续的，则存在使得

再由U(·，·)的Hölder连续性可知，存在使得

由F的Hölder连续性及(3)、(4)式，我们得

由条件(5)的假设可得

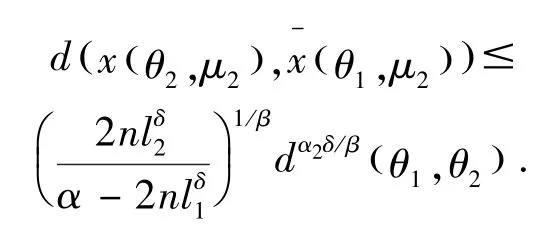
根据x(θ2，μ2)∈S1(θ2，μ2)＼S1(θ1，μ2)的任意性及距离d(·，·)的定义，我们有

结合(5)和(6)，可得

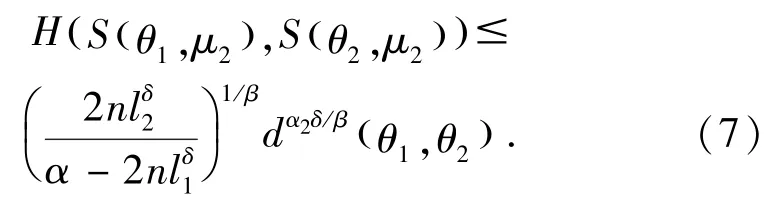
如 果S(θ1，μ2)⊂S(θ2，μ2)或S(θ2，μ2)⊂S(θ1，μ2)，我们假设S(θ1，μ2)⊂S(θ2，μ2)，由d(·，·)的定义得.因此(7)式也成立.若S(θ1，μ2)=S(θ2，μ2)，显然(7)式是成立的.

另 一 方面，假设S(θ1，μ1)≠S(θ1，μ2)，且S(θ1，μ1)⊄S(θ1，μ2)与S(θ1，μ2)⊄S(θ1，μ1).那么对任何x(θ1，μ1)∈S(θ1，μ1)＼S(θ1，μ2)，我们根据上面类似的证明思路，可得

由于β=α1δ，我们可得dβ(x(θ1，μ1)，x(θ1，μ2))≤.

根据x(θ1，μ1)∈S(θ1，μ1)＼S(θ1，μ2)的任意性，我们有

则由距离d(·，·)的定义，得

类似的，我们可以得

由(8)和(9)可得，

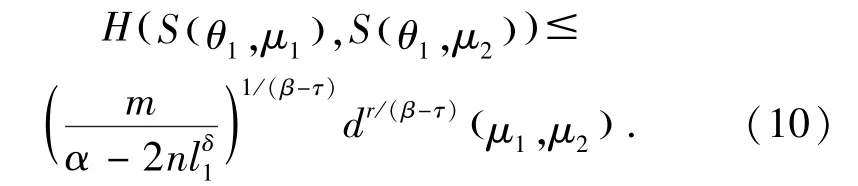
综合(7)和(10)，由Hausdorff度量的定义可得(1)式成立.定理得证.

定理3假设满足定理2的条件，设对某些ε1＞且，则，且β＞θ，则

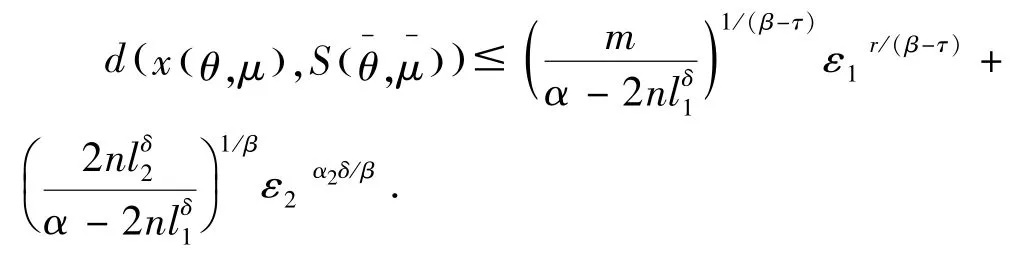
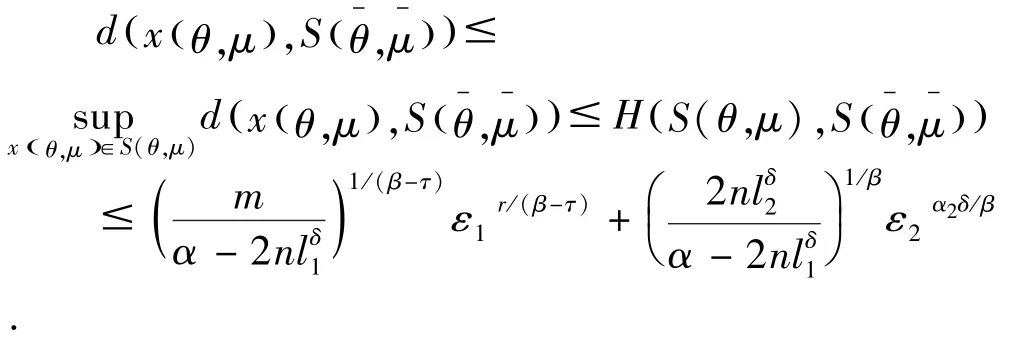
因此，该定理得证.