数学概念教学:淡化末节,把握本质
仲海峰

摘要:通过对“角的认识”教学中“什么是角?”“角的大小与什么有关?”“怎样表示平角?”等几个常见疑难问题的思考,获得感悟:数学概念教学要自觉淡化对外在形式、复杂技巧等细枝末节的关注,集中精力揭示、把握概念的本质。由此可以发现“风景”在对错之外,理解错误有时也叫“暂时性正确”,认识符号中蕴含着数学意象。
关键词:数学概念教学;数学本质;角的认识
小学阶段研究的平面图形中,角是最为特殊的一个:不具有封闭性。在判断角的大小的时候,学生常常会将其和长方形、正方形、三角形、平行四边形、圆等封闭图形的大小混为一类,产生认知偏差。本文通过对苏教版小学数学教材“角的认识”教学中几个常见疑难问题的思考,谈谈笔者对数学概念教学的感悟。
一、什么是角?——“风景”在对错之外
认识角,除了认识它的形状,还要理解它的内涵,这是比较角的大小的基础。为了帮助学生理解角的内涵,不少教师在教学中都会设计“让学生指一指物体上的角在哪儿”的活动。比如——
师(课件出示三角尺图片)这是我们常用的三角尺,你能指出三角尺上的角在哪儿吗?
(一位学生走到屏幕前,用手指指着三角尺的顶端。)
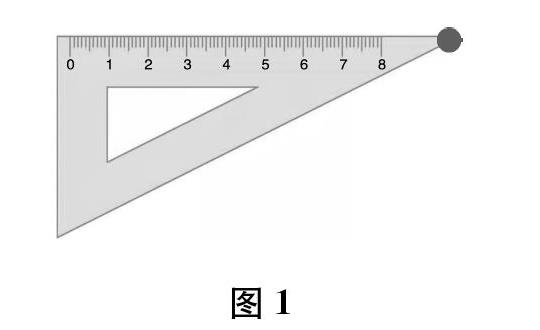
师(轻轻按下手中遥控笔的按钮,学生手指之处出现一个小圆点,如图1)你说的是这儿吗?
(学生点头。教师微笑,再次按下手中的遥控笔,课件上的三角尺渐渐隐去,只留下一个小圆点。学生一看,慌忙将指在小圆点上的手指收回。)
师同学们,他刚才指的是角吗?
生不是。他指的是角的顶点。
师那角在哪儿呢?谁再来指一指?
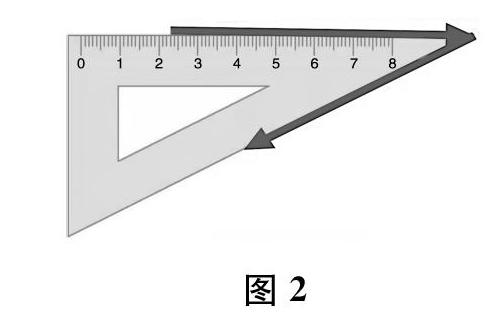
(另一位学生走到屏幕前,沿着三角尺的边“描”出角的轮廓,轨迹如图2 中的箭头所示。)
师她指得对吗?
(部分学生点头,大部分学生没有表示。)
师(同步演示,如图3)指角时,我们一般从角的顶点出发,先引出一条线,再引出另一条线。
这里,学生“指角”时,指着角的顶端,错了吗?课后访谈表明:学生指的实际上不是教师所想的角的顶点,而是“角前端尖尖的那一小部分”。这样指角指出了角最重要的部分,值得肯定。学生沿着角的边“一笔画”描出角的样子呢?这样指角清楚、明了地表示出了角的样子,也值得表扬。教师从顶点出发引出两条边呢?这样指角表示出了角的两条边无限延长的特点,渗透了四年级要学习的“角的边是射线”的知识,同样值得提倡。此外,还可以借助手指、铅笔等,从一条边出发旋转到另一条边,将角的大小具体形象地表达出来;像《几何原本》那样将角定义为“两条线之间的位置关系”。
在小学阶段,表达角的概念的方式很多,不同的方式可以帮助学生从不同的角度出发、在不同的程度上理解“两条边张开的大小”这一角的本质,都不应是“标准姿势”。教学时,教师不要过多地关注学生指角的对错,而应引导学生关注各种表达的可取之处,在比较和分析中逐步领悟角的本质。也就是说,“风景”在对错之外。
二、角的大小与什么有关?——错误有时也叫“暂时性正确”
理解角的大小与两条边张开的大小有关,是“角的认识”教学的重难點之一。为了突破重点、分解难点,不少教师在教学中都会让学生操作活动角,从中体会:将两边张开,角变大;将两边合拢,角变小。但是到了课堂练习环节,比较图4中两个角的大小时,依旧会有很多学生认为∠2>∠1。他们怎么也想不通:∠2看上去明显比∠1大,为什么老师却说它们相等呢?面对学生的困惑,教师一般都会不厌其烦地提醒:角的大小只与角两条边张开的大小有关,而与边的长短无关。
这里,“角的大小与边的长短无关”实际上存在着科学性错误:角的边是射线,射线怎么会有长短呢?但是,很多教师还是坚持用这句话来帮助学生理解角的大小。他们的理由很简单:找不到更能如此直接、有力地纠正学生亲眼所见的“∠2>∠1”这个错觉的方法。
对此,笔者的观点是:这个世界上,不是非对即错,还有一种所谓的错误也叫“暂时性正确”。二年级学生没有学过射线,在他们的眼里,角的边仅仅是直直的线段。和他们强调角的边无限长,超出了他们的认知范畴。对他们而言,“角的大小与边的长短无关”这句话可以视为“暂时性正确”。
对于“暂时性正确”,很多人一下子不容易接受。其实,这样的例子在小学阶段还有很多。如:()+7<10,()里可以填。二年级学生在横线上填“2、1、0”,显然没有填全,还可以填小数、负数等;但已经是他们能得到的所有结果了,不仅正确,甚至还要加“☆”。
当然,“退”是为了更好地“进”。不要求二年级学生理解“角的边是射线”,目的是让他们集中精力理解“两条边张开的大小”这一角的本质。等到四年级学生学习了射线,教师应该帮助他们进一步理解:角的两条边虽然有的画得长,有的画得短,但是它们的相对位置(张开的大小)可能是一样的。我们将两条边的相对位置(张开的大小)一样的角称为同类角。同类角长短不一的边可以用射线来抽象概括,最终用同一个图形来表示。
三、怎样表示平角?——符号中蕴含着数学意象
小学阶段认识图形,一个重要的学习目标是能够识图、画图。因此,学生认识了角这一图形后,不少教师都会组织学生进行辨析。比如——
(教师出示练习:图5中的图形表示的是角吗?学生解决时,对第二个图形是不是表示角,颇有争议。)
师第二个图形表示角吗?
生不是角。
生是一个特殊的角。
师意见不一致了。我们讲道理,以理服人。
生直线上有一个小圆点,这个小圆点是角的顶点,因此,第二个图形表示一个平角。
生我认为第二个图形表示的就是直线,因为直线是由无数个点组成的,那个小圆点原来就在直线上。
生我觉得第二个图形表示的是两条射线,这两条射线有一个公共的端点,而且它们在一条直线上。
……
在直线上点一个小圆点是否表示平角?貌似无聊的争论却蕴藏着基本的数学道理:数学是借助符号来表达数量关系和空间形式的,每一个符号中都蕴含着一种数学意象。例如:用直直的线表示两端无限延伸的直线;在直直的线一端点上小圆点,表示这条线从小圆点处出发,向远处延伸,也就是射线;在直直的线另一端也点上小圆点,表示这条线到此为止,不可以再延长了,也就是线段。因此,在直直的线中间点上小圆点,这个小圆点不是装饰,它表达的含义是两条射线的公共端点(如图6所示)。
既然在直线上点一个小圆点不表示平角,那么,怎样表示平角呢?这个问题需要回到角的本质来回答。角的本质是“两条边张开的大小”。我们可以借助小圆弧这一符号,形象、清楚地表示“角两条边张开的大小”。因此,平角的表示如图7所示。
对此,教师在教学中可以基于活动角的操作,引导学生思考:可以用什么符号表示角“两条边张开的大小”?得出用小圆弧这一数学符号来抽象表示。
综上可见,“角的初步认识”教学中几个疑难问题的解决其实都指向角的本质。李邦河院士告诫我们:数学“玩”的不是技巧,而是概念。数学概念教学要自觉淡化对外在形式、复杂技巧等细枝末节的关注,集中精力揭示、把握概念的本质。由此可以发现“风景”在对错之外,理解错误有时是“暂时性正确”,认识符号中蕴含着数学意象。

