集成波能转换功能的方箱—挡浪板式浮式防波堤水动力特性研究

纪巧玲，徐成浩，刘庆凯

(山东科技大学，山东 青岛 266590)

世界能源委员会调查显示，全球可利用的波浪能达20亿kW，但波浪能发电占比仅为0.4%，利用率极低。在当今化石能源逐渐枯竭，环境污染日益加剧的大环境下，如何开发利用潜力巨大的波浪能是解决当下能源问题的重要一环。张亚群等[1]对国内外波浪能发电技术及其发展现状做了综述分析，发现离岸漂浮振荡浮子式波浪能发电装置最能代表波浪能俘获装置未来的发展方向。Madhi等[2]提出了一种振荡浮子式波浪能发电装置(Berkeley-Wedge型)，可同时具有较高的波能转换效率和较好的防波性能。由于相较于传统的坐底式防波堤，浮式防波堤安装方便且便于堤内外水质交换，而建设专门的波浪能发电装置成本较高，将浮式防波堤与振荡浮子式波浪能转换装置相结合作为一种集成发电系统是较为合理的波浪能开发利用方式。

为探究此种集成系统水动力特性和能量转换效率，国内外学者开展了大量研究。Ning等[3]首先对方箱式浮式防波堤—能量转换集成系统在规则波作用下的透射系数、反射系数、浮获宽度比和垂荡响应幅值进行了初步试验研究，结果表明，适当调整PTO阻尼，可以更有效地产生电能且具有良好的防波性能。随后Zhao等[4]基于线性势流理论和特征函数匹配法，对类似的集成结构进行了数值模拟，研究了最佳PTO阻尼下集成系统的水动力特性，得到与Ning等[3]试验相同的结论。毛艳军等[5]基于OpenFOAM程序对同样的集成系统在PTO装置影响下的水动力特性进行了研究，研究发现在一定范围内适当增大PTO阻尼系数可提高集成系统的波能俘获宽度比。刘崇期[6]对该类集成装置的水动力试验研究表明，集成装置的PTO阻尼力、吃水、相对宽度和波长对系统的水动力特性有显著影响，能量转换效率对应一个最佳的阻尼系数，且波浪透射系数随阻尼系数的增大而减小。以上学者的研究表明，波浪能集成系统的能量转换效率与系统PTO阻尼的变化有关。Chen等[7]对Ning等[3]的方箱结构进行了改良，结果表明，将矩形浮子的底角直角改为圆角能有效提升集成系统的能量转换效率，说明浮子的形状对集成系统的能量提取效率有影响。张恒铭等[8]采用Star-CCM对方箱型、三角型、三角型加挡板、Berkeley-Wedge型这4种型式的集成系统进行了水动力性能研究，结果表明加挡板后的三角型模型在防波性能与能量转换性能上都要明显优于无挡板的三角型模型。

幕帘式防波堤是一种常用的透空式防波堤，其结构简单，施工快捷，维护容易，具有极大的推广价值。王世林等[9]对方箱—垂直板浮式防波堤的水动力特性进行了研究，结果表明在方箱底部增加垂直挡浪板可提高浮式防波堤的防波性能，但其并未探究该结构型式作为波浪能转换集成系统的波能转换特性。由此，这里在Ning等[3]研究的方箱型浮式防波堤—波浪能转换集成系统的基础上，在方箱底部的背浪侧增加垂直挡浪板，形成方箱—垂直板式浮式防波堤—波浪能转换集成系统。基于N-S方程建立数值模型，运用紧致插值曲线(CIP)方法[10]求解流场，流体体积(VOF)方法[11]捕捉自由面，浸没边界法(IBM)处理流体与浮体的耦合。运用数值模型开展该新型集成系统的水动力特性和能量转换特性研究，探讨PTO阻尼力的变化以及挡浪板的有无和长度对集成系统的入、反射系数和能量转换率的影响，研究成果对该类结构的工程设计具有一定的参考价值。

1 数学模型

将流体设定为不可压缩、非定常，控制方程为二维N-S方程，其连续性方程和动量方程表达式为：

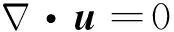
(1)

(2)

式中：u为速度矢量，μ为动力黏性系数，p为压强，ρ为流体密度，F为质量力矢量。

在直角笛卡尔坐标系统下求解模型，采用VOF方法进行自由面捕捉，并采用多相流理论来处理模型中的固相和液相，两者满足以下控制方程：

(3)

式中：φm(m=1，2，3)是气相、液相、固相三相的体积函数，分别表示了气、液、固三相在同一个计算网格内所占的体积分数，三者满足φ1+φ2+φ3=1。求解出φm后，可用式(4)求得同一网格单元内的流体属性：

(4)

式中：λm表示各相的流体属性值，λ为一个网格内的平均流体属性(流体的密度ρ或动力黏性系数μ)。

2 模型的数值求解

采用分步法求解N-S动量方程，以CIP方法离散对流项，以中心差分法求解扩散项，以逐次超松弛(SOR)方法求解压力项。CIP方法[10]是一种求解双曲偏分方程的半拉格朗日方法，其核心思想是以网格点上的变量值及其一阶空间导数为基础构造三次多项式来近似变量在网格内的变化,确保了时间跟空间上的三阶精度，具有振荡小、精度高、计算效率快等特点。赵西增等[12]用此方法模拟了溃堤与极端波浪对浮式结构的冲击过程，模拟结果与试验吻合较好，验证了该方法用于求解非线性流场的准确性，这也为采用CIP方法求解流场提供了理论基础。

2.1 边界条件

1) 追踪自由面边界。为了追踪自由面的非线性波动，采用VOF类型的THINC/SW方法[11]进行自由面重构。该方法运用双曲正切函数来构造水气两相界面的通量，具有通量守恒、无伪振荡、界面准确锐利的特点，适用于复杂的自由面大变形。

2) 流固耦合。采用浸没边界法(IBM)[13]处理浮体与流体之间的流固耦合问题，其确定单元网格整体速度的表达式为：

U=Ubφ3+u(1-φ3)

(5)

式中：U为单元网格的整体速度，Ub为浮体的局部速度，u为求解公式(2)得到的流场速度，φ3为固体项的体积函数。

3) 造波边界。采用动量源造波法[14]来生成入射波，该方法通过对流体施加一个周期性变化的动量来实现造波，可有效避免边界造波法产生的波浪二次反射问题。在速度场中加入的水平方向动力源项函数为：

s=-g(2βx)exp(-βx2)(D/ω)sin(-ωt)

(6)

式中：ω是波浪角频率，β是造波区宽度的相关参数，D是源函数。

2.2 浮体运动公式

集成系统浮体运动响应方程为：

(7)

式中：M为浮体质量，Fy为波浪垂向作用力，FPTO为系统PTO阻尼力，ζ为浮体垂向运动响应幅值，g为重力加速度。

浮体运动响应方程为二阶偏微分方程，四阶龙格库塔法在求解二阶偏微分方程方面具有计算速度快、精度高等优势[15]，采用该方法进行浮体运动响应方程的求解可获得更高的精度，该方法多应用于浮式海洋平台动力响应方程的求解[16]。

2.3 集成装置波能转换效率

反射系数Kr定义为反射波高Hr与入射波高Hi之比，透射系数Kt定义为透射波高Ht与入射波高Hi之比，入反射系数通过Goda两点法计算。耗散系数Kd为装置的动能、俘获的波浪能及流体黏性等耗散能的总和，Kr、Kt、Kd存在如下关系：

(8)

集成装置的俘获宽度比ηe等于装置俘获波浪能功率Pc与入射波功率Pi之比，为：

ηe=Pc/Pi

(9)

其中，Pc为集成系统俘获波能的功率。

(10)

式中：FPTO为波能转换装置的阻尼力，采用常数型式；u为浮体的运动速度；T为波浪周期。

入射波功率计算公式为：

(11)

式中：ρ为海水密度，g为重力加速度，H为波高，L为波长，T为波浪周期，h为水深。

3 水槽布置及数值模型验证

3.1 数值水槽布置

假定浮箱所处海域的海况为波高2.0 m，水深10.0 m，周期4.03～6.32 s，根据工程实际假定原型浮箱尺寸为8 m×6 m×7.8 m(长×高×宽)，吃水深度2.425 m，挡浪板尺寸为1.0 m×7.8 m×0.6 m(长×高×宽)；参考Ning等[3]的试验，按照弗劳德相似1∶10的比例得到浮箱的缩尺模型，开展数值计算。缩尺模型参数如下：浮箱高D=0.6 m，长B=0.8 m，宽W=0.78 m，质量M=156 kg，浮箱吃水深度s=0.242 5 m，挡浪板长Sp=0.1 m，宽sb=0.78 m，厚b=0.06 m。波浪数值水槽设置如图1所示，坐标原点在源造波区中心的静水平面处，x轴水平向右，y轴竖直向上。水槽总长25 m，静水深h=1.0 m。为避免波浪反射的影响，在水槽两端设置消波区，左侧设置8 m的消波区，右侧消波区长度为10 m。集成系统模型放置在水槽5.6～6.0 m处，模型周围的网格进行加密布置，dx=4 mm，dy=1 mm。模型两侧布置6个波高测点，分别放置在水槽x=2.75 m、3.00 m、3.25 m、9.00 m、9.25 m、9.50 m处，测点间隔0.25 m。除在背浪侧方箱底部增设挡浪板外，为探究挡浪板长度与PTO阻尼力对集成装置的影响，参考Ning等[3]试验中相对宽度B/L=0.22的工况参数及试验结果对相关参数进行设置。在阻尼力小于40 N时，集成系统的俘获宽度比较小，工作效率较低，工程实际意义不大，而阻尼力大于300 N后集成系统俘获宽度比极小，波能转换效率接近0，因此选取阻尼力40～300 N作为研究的主要区间，具体工况参数见表1。

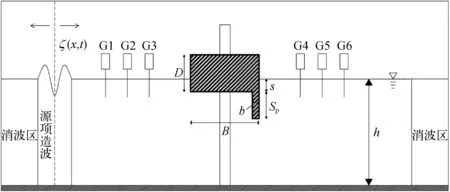
图1 数值水槽布置示意Fig. 1 Schematic diagram of the numerical flume

表1 工况参数表Tab. 1 Condition parameters

3.2 造波与数值模型验证

为验证模型的造波稳定性，采用文中的数值模型进行规则波的造波验证，目标波的振幅A=0.062 5 m，周期T=1.58 s。图2给出了数值造波结果与理论值的比较，可见数值造波的振幅与周期均与理论值较为吻合，说明文中模型数值造波精度较好。

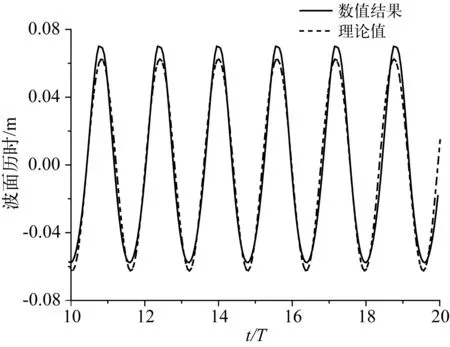
图2 数值造波与理论值对比Fig. 2 Comparison of wave surface elevation with the theoretical result

为验证数值模型计算波浪与结构物相互作用的精度，对二维矩形浮箱在规则波作用下的垂向波浪力进行计算，试验工况如下：宽度为2b的矩形浮箱固定在水深h=5b的水槽中，吃水为b，其中kb=0.4，Ab=0.1，b=0.25 m，即规则波振幅A=0.625 m，周期T=1.58 s。图3给出了文中的数值结果与Chen等[7]的数值结果和Marcos及Johannes[17]的试验结果的比较。图3中可以看出，文中模型结果垂向波浪力负峰值的拟合度略差，大于试验结果，与Chen等[7]的垂向波浪力负峰值偏大的趋势一致，但偏大幅度略大。由于实际试验中浮箱两侧与水槽壁之间留有一定缝隙防止浮箱与水槽壁产生摩擦，这与数值模拟中纯二维的设置有所不同，可能导致数值模拟结果与试验值存在一定差别。文中模型模拟的垂向波浪力正峰值结果与试验结果吻合良好，曲线较为平滑，而Chen等[7]的数值结果存在一定的振荡现象。总体上，文中数值模型可以较为准确地模拟规则波与结构物的相互作用。

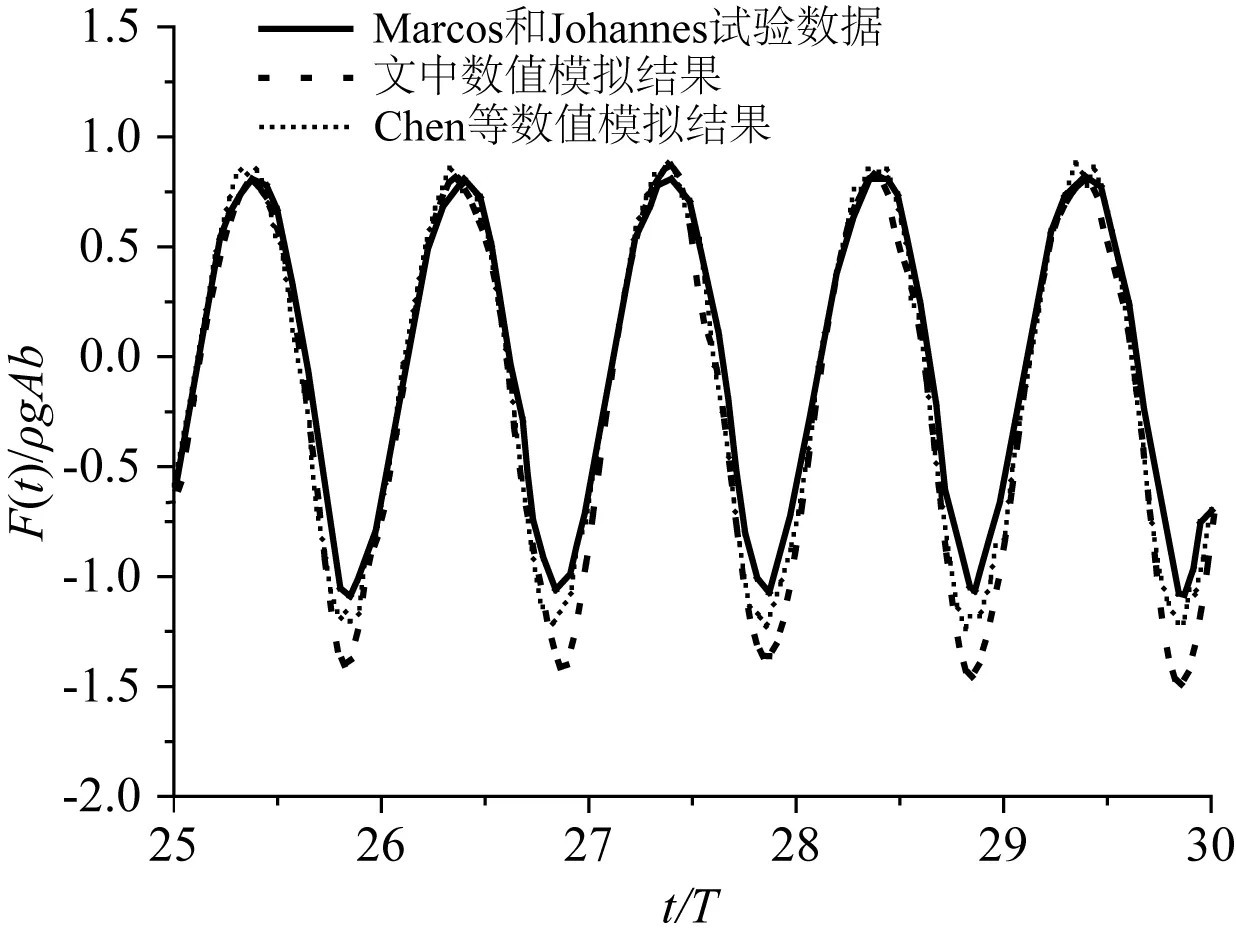
图3 方箱垂向波浪力数值模拟结果与试验结果的比较Fig.3 Comparison of numerical results with experimental results for the vertical wave force of a fixed square box

4 集成系统水动力特性和能量转换特性研究

4.1 PTO阻尼的影响

图4给出了PTO阻尼力对集成系统水动力特性和能量转换特性的影响曲线，总体影响趋势与Ning等[3]试验结果趋势相同。

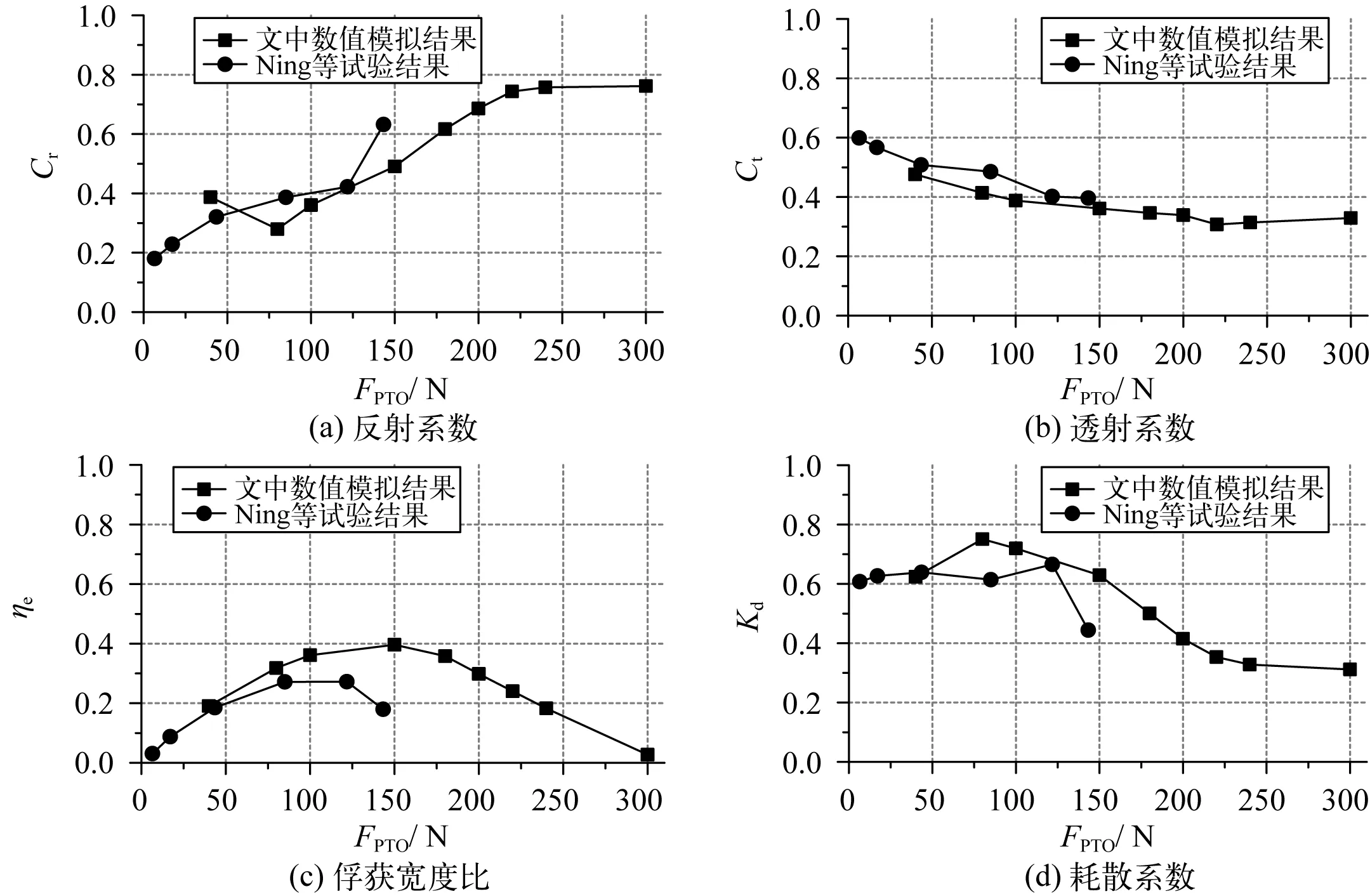
图4 集成系统不同阻尼力下的水动力特性和能量输出特性 Fig. 4 Hydrodynamic characteristics and power take-off characteristics of the integrated system under different damping forces

由图4(a)可知，集成系统的反射系数总体随阻尼力的增大而增大，在阻尼力增大到220 N后趋于稳定，此时反射系数Cr=0.743 4，且反射系数不再随阻尼力的增加而出现明显变化。在阻尼力增大到一定值后，相比Ning等[3]试验中的方箱型集成系统，增设挡浪板后集成系统的反射系数更小。图4(b)中集成系统的透射系数随阻尼力的增大而减小，在阻尼力增大到220 N后集成系统的透射系数趋于稳定，此时透射系数Ct=0.307 2。与Ning等[3]的方箱型试验结果对比可知，增设挡浪板后集成系统的透射系数变小。Koutandos等[18]和He等[19]指出防波堤的透射系数Ct小于0.5通常被认为该防波堤运行状况良好，由此说明增设挡浪板后集成系统的防波性能要好于方箱型。图4(c)中集成系统的俘获宽度比随阻尼力的增大呈现先增大后减小的趋势，这与Ning等[3]试验结果趋势相同，且在阻尼力为150 N时达到最大，此时俘获宽度比ηe=0.396 4，透射系数Ct=0.361 1。增设挡浪板后，集成系统的适用范围更广，可在更广的PTO阻尼力范围内保持较高的工作效率。此外，相比Ning等[3]方箱型波浪能集成系统，在方箱底部背浪侧增加挡浪板后集成系统最大能量转换效率提升33%左右，由此表明增设挡浪板对提高集成系统的波浪能转换效率具有积极作用。此外，在阻尼力为300 N时，集成系统由于阻尼力过大导致在波浪力的作用下浮箱几乎不产生垂荡，进而发生集成系统能量转换效率近乎为0的现象。由图4(d)可知，集成系统的耗散系数随阻尼力的增大呈现先增大后减小的趋势，在阻尼力为80 N时达到最大，此时耗散系数Kd=0.750 7。与反射系数、透射系数类似，集成系统的耗散系数在阻尼力增大到220 N后趋于稳定，此时的耗散系数Kd=0.353 0。增设挡浪板后集成系统的耗散系数大于方箱型能量转换集成系统，由此说明增设挡浪板后集成系统对波浪的俘获能力更强，系统工作性能更好。综上，增设挡浪板可有效提高集成系统的防波性能和能量转换性能，可使集成系统在较广PTO阻尼力范围内保持较高的工作效率。

表2 不同FPTO时各项能量系数Tab. 2 Energy coefficients when FPTO=80 N and 150 N

4.2 涡量场分析

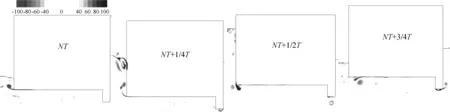
图5 FPTO=150 N下浮子底部涡量场Fig. 5 Vorticity field under the bottom of float with FPTO=150 N

当入射波与浮箱相互作用时，浮箱周围的流场产生涡流，在周期波的作用下，浮箱的角落处及挡浪板下部涡流交替产生和移动。从NT到NT+1/4T，浮箱向下运动至位移极小处，运动速度逐渐减为0。在浮箱向下运动过程中，入射波与浮箱发生碰撞反射了大部分波能，其吃水逐渐增大，反射波与入射波相互叠加生成的叠加波波高增大，波形变陡，出现波浪破碎现象。NT时刻由于前一个入射波波尾刚刚离开浮箱，下一个入射波刚刚到来，浮箱右侧挡浪板底部流体还未受到入射波的影响，未产生明显涡流，此时浮箱向下运动与入射波相互作用在其左下角生成顺时针的涡流。NT+1/4T时刻，左下角产生的顺时针涡流向上方脱落并与入射波发生碰撞进而逐渐消散，挡浪板底部的流体在入射波的作用下与浮箱后侧的流体相互作用形成顺时针涡流。与传统的方箱式浮式防波堤相比，增加挡浪板后，浮箱背浪侧产生的涡流深度更大，对入射波的能量耗散更明显。从NT+1/4T到NT+1/2T，浮箱向上运动至平衡位置，同时速度达到最大。在入射波的作用下，浮箱左下角和挡浪板底部形成向后的压力梯度，在两处皆形成逆时针的涡流，且前一时刻在挡浪板底部生成的顺时针涡流还未完全消散，因此挡浪板下部形成了逆时针涡流叠加前一时刻顺时针涡流的现象，从而增加了能量的耗散。从NT+1/2T到NT+3/4T，浮箱向上运动至平衡位置，同时速度达到最大，浮箱前侧水深逐渐减小。在浮箱前侧水流与入射波的共同作用下，浮箱下部产生的逆时针涡流逐渐生长并传播到更远处。与此同时一对新的方向相反的涡旋又在浮箱左下侧与挡浪板底部生成，开始下一个涡脱落周期。在整个波浪周期中，顺时针的涡旋主要与入射波发生碰撞而逐渐消散，逆时针的涡流逐渐生长并向后方脱落。

综上，集成系统在对波浪的消减过程中存在多种能量损耗方式，涉及到涡脱落、波浪反射与破碎、电能转换等。首先，入射波在经过浮箱时，与其发生碰撞，在浮箱前侧产生波浪破碎与反射，该过程造成了入射波能量的损耗。背浪侧增设的矩形挡浪板增加了防波堤的波浪消减深度与涡流的强度，有效阻挡了浮箱下方区域波浪的传播，减小了波浪的透射系数，增强了防波堤的消浪性能。其次，浮箱左下角与背浪侧挡浪板底部涡流的产生和脱落会造成局部流体的无序运动，其对入射波所产生的附加切应力等价于增加了浮箱的有效吃水深度。浮箱底部增设的挡浪板增加了浮箱的附加质量，且经由挡浪板反射的波浪与入射波在浮箱底部相互叠加使得浮箱的振幅进一步增大，进而增强了集成系统的波浪俘获能力。最后，能量转换装置的PTO阻尼力，减小了浮箱垂荡运动的幅值，使其在相同的波浪条件下产生更小的位移，进而增大对入射波的反射面积，提升浮式防波堤的防波性能。

4.3 挡浪板长度的影响

图6为集成系统水动力特性与能量转换特性随挡浪板长度增加的变化趋势，图6(a)中集成系统的反射系数随挡浪板长度的增加而减小，挡浪板长度Sp=0.0 m时反射系数最大，此时Cr=0.517 3，在Sp=0.5 m处趋于稳定，此时Cr=0.270 5。图6(b)中集成系统的透射系数随挡浪板长度的增大呈现先增大后减小的趋势，最大值出现在Sp=0.1 m处，此时Ct=0.350 9，在挡浪板长度Sp=0.5 m时趋于稳定，此时透射系数Ct=0.086 2。从图6(c)中可以看出，集成系统的俘获宽度比随挡浪板的长度增加而增大，在Sp=0.5 m时达到最大，此时ηe=0.563 1。由于入射波主要为表面波，水深增大到一定程度后下层流体中所蕴含的波浪能较少，此时增加挡浪板长度对系统俘获宽度比影响较小，而集成系统质量在挡浪板长度增加后有所增大，导致在Sp=0.6 m时集成系统的波浪能转换效率有所下降。此外，考虑到结构稳定性的问题，未再继续探究更长挡浪板对集成系统水动力特性与能量转换特性的影响。图6(d)为集成系统耗散系数随挡浪板长度增加的变化趋势，曲线总体呈现上升趋势，在Sp=0.1 m处稍有下降，此时Kd=0.628 9，曲线在Sp=0.5 m时趋于稳定，此时Kd=0.919 4。挡浪板长度Sp=0.1 m时透射系数较大，导致入射波能量损失较多，进而出现耗散系数小于方箱型能量转换集成装置的情况。图6(b)中增设0.1 m挡浪板的集成系统透射系数大于未增设挡浪板的集成系统，其主要原因为：Sp=0.0 m时，浮子动能W动=5.10 J,Sp=0.1 m时，W动=10.66 J，结合图6(a)可得，相较于Sp=0.1 m，Sp=0.0 m时浮子垂荡幅度较小，入射波在与浮体发生碰撞后大都以反射波的形式折回，只有少量入射波从下部穿过，而Sp=0.1 m时浮子垂荡幅度较大，导致更多的入射波从浮体下部穿过，进而出现Sp=0.0 m透射系数小于Sp=0.1 m的现象发生。

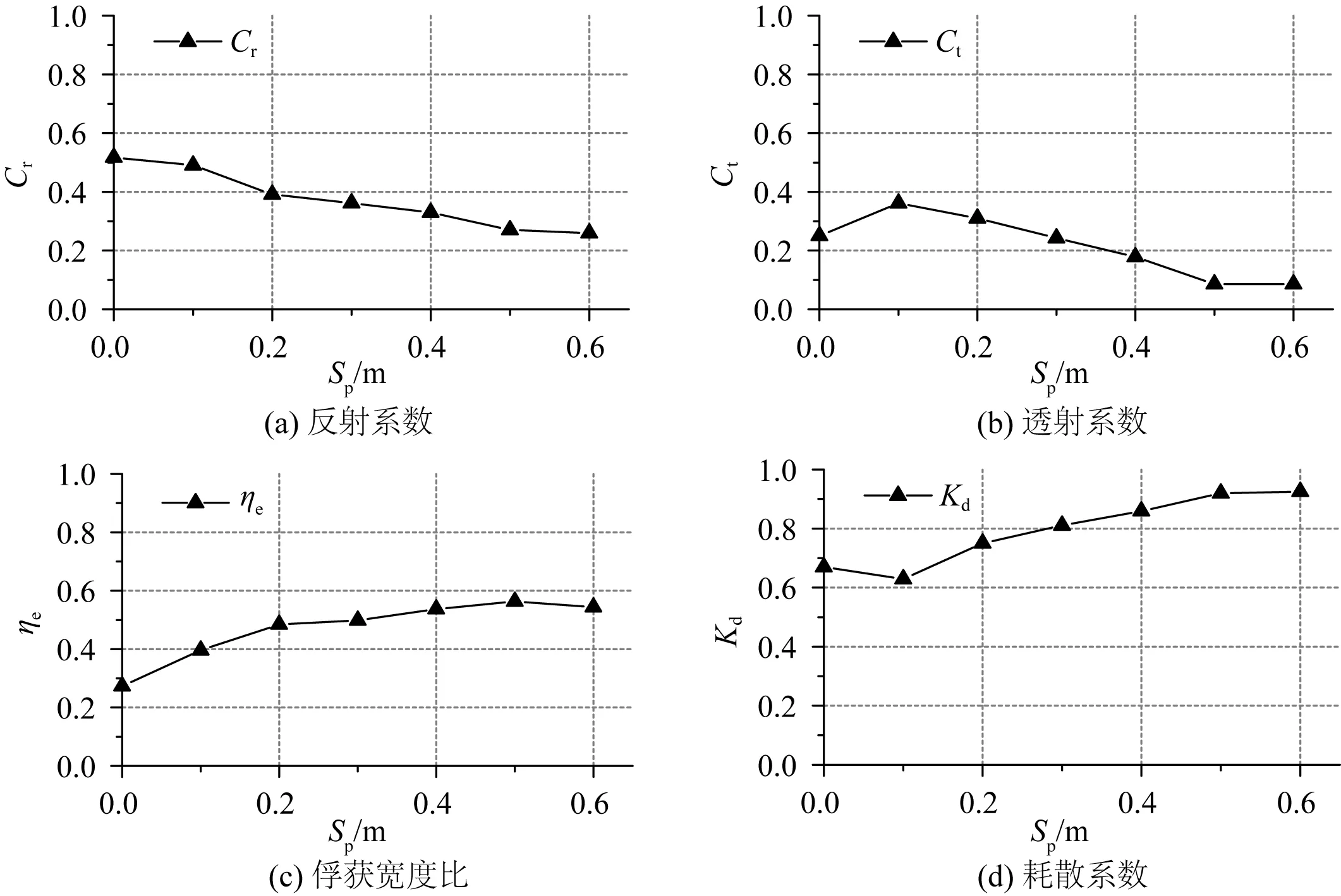
图6 集成系统不同挡浪板长度下的水动力特性和能量输出特性Fig. 6 Hydrodynamic characteristics and power take-off characteristics of the integrated system with different lengths of the verical wave board

5 结 语

采用N-S方程作为流体控制方程，基于紧致插值曲线(CIP)方法结合浸没边界法求解流场，在Ning等试验研究的基础上探究阻尼力FPTO的变化以及挡浪板的有无和长度变化对方箱—垂直挡浪板浮式防波堤—波浪能转换集成系统的水动力特性和能量转换特性的影响，得到如下结论：

1) 方箱—垂直挡浪板浮式防波堤—波浪能转换集成系统(挡浪板长度Sp=0.1 m)的透射系数Ct随PTO阻尼力的增大而减小，在FPTO=220 N后，透射系数不再随阻尼力的变化而出现明显波动，此时Ct=0.307 2。集成系统的俘获宽度比ηe随阻尼力的增大呈现先增大后减小的趋势，在FPTO=150 N时达到最大，此时ηe=0.396 4。

2) 对比Ning等试验中的方箱型浮式防波堤波浪能转换集成系统，增加0.1 m的挡浪板后集成系统最大俘获宽度比提高33%左右，且透射系数小于方箱型，此时集成系统具有更高的能量转换效率和防波性能，可在较广PTO阻尼力范围内保持较高的工作效率。

3)集成系统的透射系数总体随挡浪板长度的增加而减小，在挡浪板长度增大至0.5 m后集成系统的水动力特性趋于稳定，不再随挡浪板长度的变化而出现较大的波动，此时Ct=0.086 2。俘获宽度比随挡浪板长度的增加而增大，在Sp=0.5 m时达到最大，此时ηe=0.563 1。