基于环境包络线法的深水浮式平台极值响应长期预报

宫浩男，谢波涛，王俊荣，宋佳奇，刘 浩

(1. 中国海洋大学 工程学院，山东 青岛 266100; 2. 中海油研究总院有限责任公司，北京 100028)

远洋航行的船舶及其他海洋结构均受到波浪、风、流等不断变化的环境荷载影响，需要对结构进行概率可靠性分析，以确保结构长期安全可靠。原则上，应考虑到各种短期环境的出现概率及该条件下结构最大响应分布，对结构进行全面的长期响应分析[1]。但长期响应分析计算量大而且耗费时间。为了提高计算效率，可开发使用少量短期响应分析的近似方法来简化计算。

海洋结构设计中，尤其是在结构设计的早期阶段，利用环境包络线完成深水浮式结构物可靠性设计已成为目前的研究热点。环境包络线法(ECM)[2-3]基于逆一阶可靠性方法(IFORM)在环境参数空间中根据相关概率分布来定义环境概率等值线，沿着包络线对有限的关键海况进行短期荷载和响应计算，进而通过选定适合的短期响应分位数来估计结构物的特定重现期响应。该方法已广泛用于海洋结构设计中，例如Baarholm等[4]采用环境包络线法估计重力式平台的倾覆力矩和基底剪力，Fontaine等[5]采用环境包络线法评估了西非现有浮式液化天然气生产储卸装置(FPSO)系泊系统的可靠性，Muliawan等[6]比较了包络线法预测的系泊张力ULS响应和综合各海态估计的系泊张力ULS响应，Li等[7]提出了一种改进的固定式风机环境包络线法(MECM)用以识别控制特定重现期响应最重要的环境条件，Fitzwater等[8]用环境包络线法估算风力涡轮机的设计载荷。描述海洋环境条件的模型对绘制环境包络线极为重要，模型对环境条件的描述精度将直接影响包络线绘制后对结构特定重现期响应的预测。环境包络线法常用的波浪模型是Haver[9]提出的一个双变量对数正态和威布尔(lonowe)混合模型，用于描述波浪有效波高Hs和谱峰周期Tp的边际分布。此外，描述波浪有效波高Hs和跨零周期Tz的模型包括二元参数模型和多个基于Copulas参数族的模型[10]。

利用中国南海荔湾海域40年波浪模拟数据，建立Weibull-Gev条件分布模型用于描述该海域波浪环境，并基于IFORM方法，绘制荔湾海域十年、百年、千年一遇的有效波高Hs—谱峰周期Tp环境包络线。通过对张力腿平台(TLP)进行长期分析，给出南海TLP在波浪作用下应用环境包络线法估计百年一遇张力腿张力的分位数，进而为张力腿平台长期张力极值预报提供有效的近似方法。

1 长期响应分析

1.1 逆一阶可靠性方法

工程应用中波浪统计建模的方法是假定海洋表面构成一个在时间上平稳空间上均匀的随机波场。实际上，波浪仅在有限的一段时间d内具有平稳性，这称为波场的短期描述，中国南海的短期持续时间d通常取为3 h。对于波场的长期描述，可视其由多个短期描述组成，两个连续的短期描述之间没有过渡期[11]。

长期响应预报认为各种不同海况组成的短期预报相互独立，波浪载荷的长期分布是各短期概率分布的加权组合。长期预报通过以3 h持续时间的短期海况中结构最大响应X3 h作为目标变量来完成。N年一遇的响应估计可通过对所有短期环境条件下结构短期响应进行卷积得到[11]。

X3 h的长期分布可通过以下积分得到(保守地假设所有环境条件来自同一方向)：

(1)

其中，FX3 h(x)为结构长期响应极值的累计概率分布。FX3 h|HsTp(x|h,t)是结构在海况(Hs,Tp)下3 h响应极值的条件概率分布。fHsTp(h,t)为有效波高和谱峰周期的长期联合概率密度函数。

为了估计结构特定重现期响应，必须计算与3 h持续时间对应的年度超越概率。将每年预期的短期海况数记为md=365×24/3=2 920，则N年一遇响应对应的超越概率(失效概率)为：

(2)

对应的结构功能函数可表示为：

g(xcrit;X3 h,Hs,Tp)=xcrit-X3 h(Hs,Tp)

(3)

其中，xcrit为给定的响应阈值，则失效概率可以通过式(4)估算：

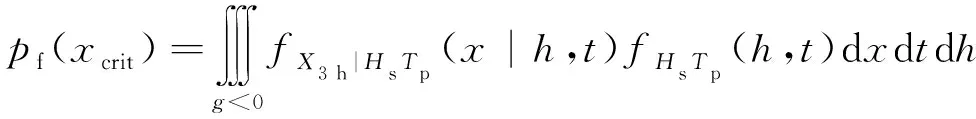
(4)

式(4)积分可以通过一阶可靠性方法进行近似而无需显式积分。通过Rosenblatt变换将参数转换为独立的标准正态变量U1，U2和U3：

(5)

其中，Φ为标准正态分布函数。变换后的结构功能函数为z=g(xcrit;X3 h,Hs,Tp)=g(xcrit;U1,U2,U3)，结构的失效概率可以写作：

(6)

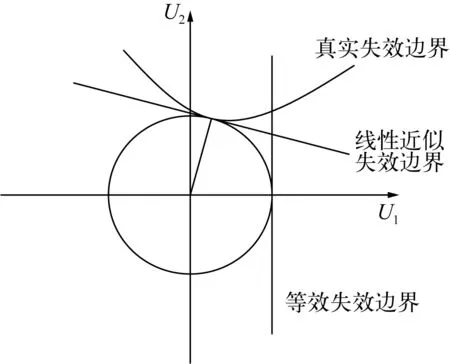
图1 二维标准正态空间中的失效边界、线性失效边界和等效失效边界Fig. 1 Failure boundary,linearized failure boundary and equivalent failure boundary in U-space

(7)

(8)

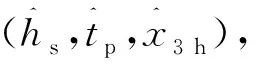
1.2 环境包络线法

环境包络线是指与恒定超越概率对应的环境概率等高线，可用于估计复杂结构特定重现期的响应，但需要时域模拟或模型测试来计算结构短期响应极值的概率分布。主要研究波浪有效波高Hs与谱峰周期Tp的包络线。

1.2.1 有效波高—谱峰周期的包络线

对于某给定的IFORM问题，若短期响应极值分布很集中，即X3 h的变异性很小，fX3 h|HsTp接近狄拉克δ函数，则可以用均值代替该变量，在标准正态空间中取该变量的中位数，将随机变量U3替换为U3≡0来简化问题。那么设计点将在U1-U2平面上以原点为圆心，β为半径的圆上的某个位置。根据角度θ利用式(9)将圆离散为一组点uj=(u1j,u2j)。

(9)

利用等式(5)将离散后的点利用Rosenblatt变换转换至Hs-Tp空间，即可得到闭合的Hs-Tp包络线。图2为圆上的点从标准正态空间U1-U2转换回环境参数Hs-Tp空间的示意。

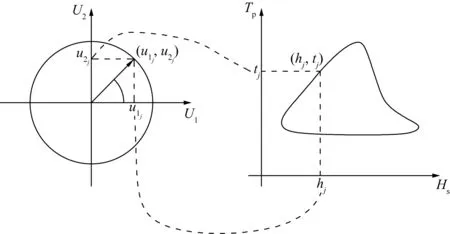
图2 圆从标准正态空间转换回Hs-Tp空间Fig. 2 Converting data from U-space to physical parameter space

1.2.2 包络线法估计结构长期响应

对于大多数的实际问题，不能简单地假设X3 h的分布很窄。应用如图2右侧所示的环境包络线需要用较高的分位数来代替中位数，以确保结构的安全性。研究发现，结构短期响应X3 h的变异系数(coefficient of variation)取值范围通常为0.1～0.2，因此可以推荐一个分位数α来估计一类响应问题的极限响应[2]。

假设在有效波高和谱峰周期定义的海况下，结构3 h响应极值遵循具有位置参数μ、比例参数σ和形状参数k的广义极值分布(Gev)：

(10)

其中，μ=μ(Hs,Tp)，σ=σ(Hs,Tp)，k=k(Hs,Tp)，结构的极限响应可表示为：

(11)

2 环境包络线法在中国南海的应用

利用中国南海荔湾海域1979年1月至2018年12月的波浪模拟数据(40年波浪散点如图3所示)，绘制有效波高—谱峰周期联合概率包络线，对比张力腿平台的长期预报结果，给出环境包络线法估计南海TLP百年一遇张力极值采用的分位数α。

图3 荔湾海域波浪散点Fig. 3 Wave scatter diagram of Liwan Sea area

2.1 环境条件分布模型

在环境包络线法中通常利用Weibull-Lognorm模型来描述有效波高和谱峰周期的联合概率分布[13]，即采用Weibull分布作为有效波高的边际分布，并用对数正态分布来拟合谱峰周期在某一波高条件下的分布。但文中研究发现荔湾海域谱峰周期在某一波高下的分布并不服从对数正态分布(如图4所示)，而采用广义极值分布(Gev)拟合的拟合优度更高(如图5所示)。因此将波浪数据按照有效波高自小至大排序后，数据按序每100个一组共分为3 441组，对每组的谱峰周期进行广义极值分布拟合并进行KS检验，显著性水平取0.05，其中3 087组返回值为0，服从广义极值分布，故可认为在某一有效波高条件下的谱峰周期服从广义极值分布。

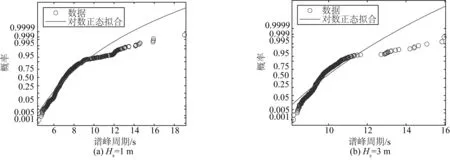
图4 对数正态分布拟合谱峰周期条件分布Fig. 4 Log-Normal distribution used to fit the conditional distribution of spectral peak period

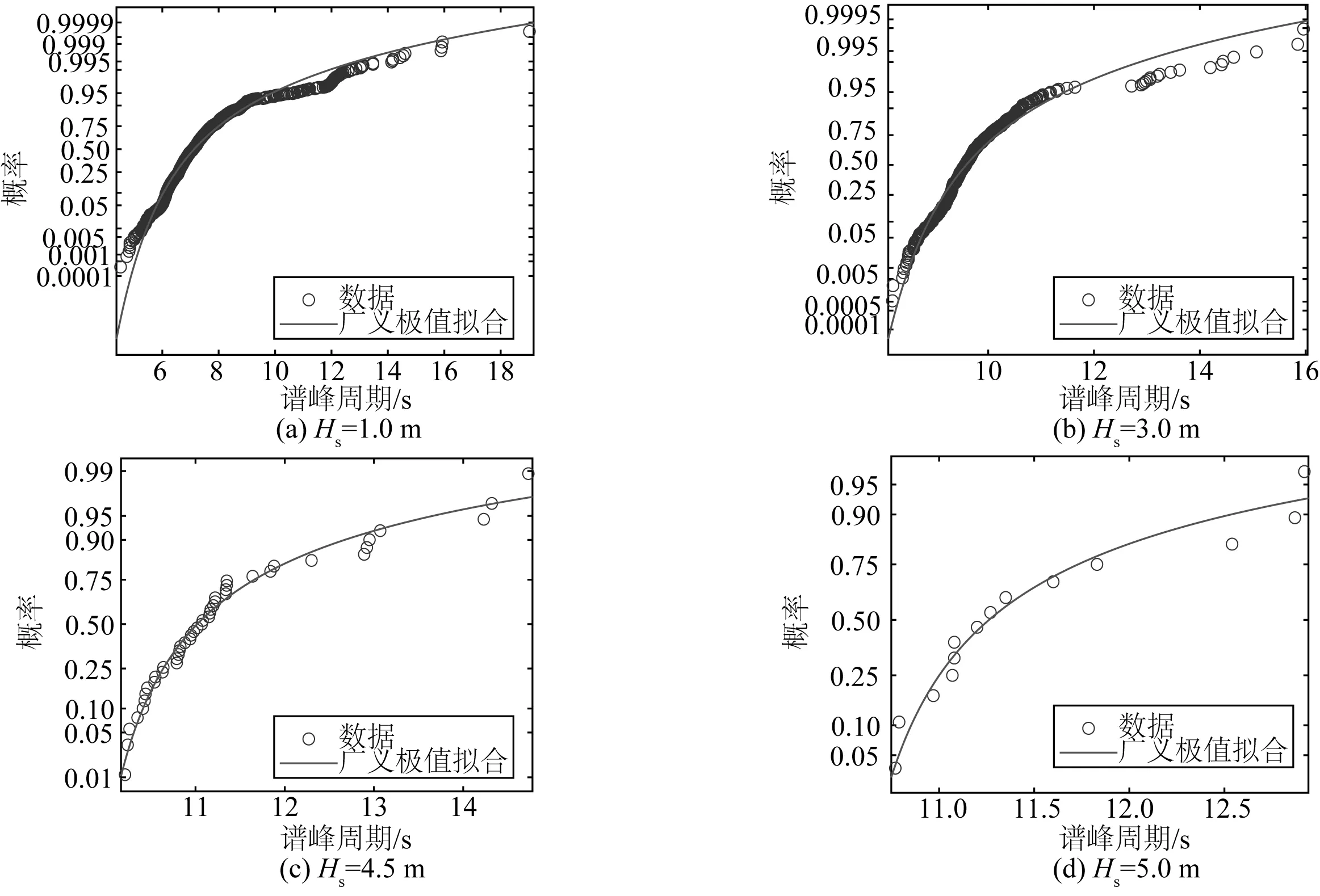
图5 广义极值分布拟合谱峰周期的条件分布Fig. 5 Gev distribution used to fit the conditional distribution of spectral peak period

有效波高Hs的边际分布由Weibull分布描述，采用Weibull-Gev分布的条件建模方式描述荔湾海域波浪长期分布：

fHsTp(h,t)=fHs(h)fTp|Hs(t|h)

(12)

(13)

(14)

其中，参数k(h)、μ(h)和σ(h)是给定Hs后，根据给定Hs的范围(文中取变量间隔为0.3 m)，变量Tp广义极值分布拟合的3个参数。有效波高的Weibull拟合参数如表1所示，其中α为比例参数，β为形状参数。

表1 有效波高的Weibull分布拟合参数Tab. 1 Weibull distribution fitting parameters of significant wave height

为了推断超出数据范围的谱峰周期的Gev拟合参数，观察参数的变化趋势后(如图6所示)，将参数的估计值拟合为下列形式的平滑函数：

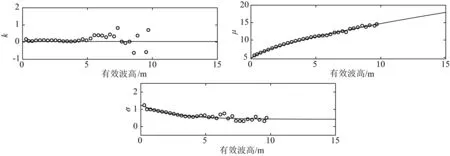
图6 谱峰周期Tp的广义极值分布参数的拟合结果Fig. 6 The fitting results of the estimated parameters for the marginal generalized extreme value distributions of Tp

k(h)=C=0.037 86

(15)

μ(h)=a1+a2ha3

(16)

σ(h)=b1+b2eb3h

(17)

拟合参数结果见表2。

表2 用以拟合Gev参数的平滑函数参数Tab. 2 Smoothing function parameters used to fit the Gev parameters

2.2 荔湾海域Hs-Tp概率包络线图

根据2.1节建立的环境条件模型，将标准正态空间中半径为β的圆利用Rosenblatt逆变换到物理参数空间即可得到闭合的荔湾海域Hs-Tp包络线(见图7)。

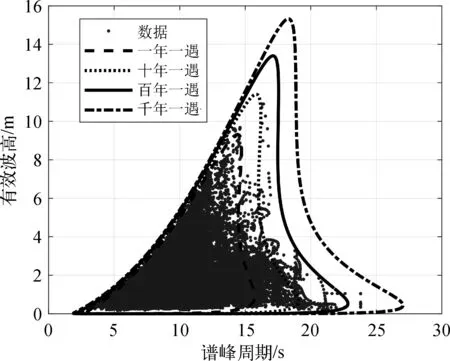
图7 荔湾海域各重现期的环境包络线Fig. 7 Environmental contour lines for Liwan sea area at different return periods

2.3 南海环境包络线在TLP平台的应用

以一座深水TLP平台为例，将文中所研究方法用于该平台张力腿张力百年一遇响应预报。该平台作业水深为1 500 m，立柱直径23.75 m，设计在位吃水30 m，排水量73 658 t，平台主尺度参数见表3。该平台共配置12根张力腿，每个立柱/角落3 根，张力腿布置如图8所示。

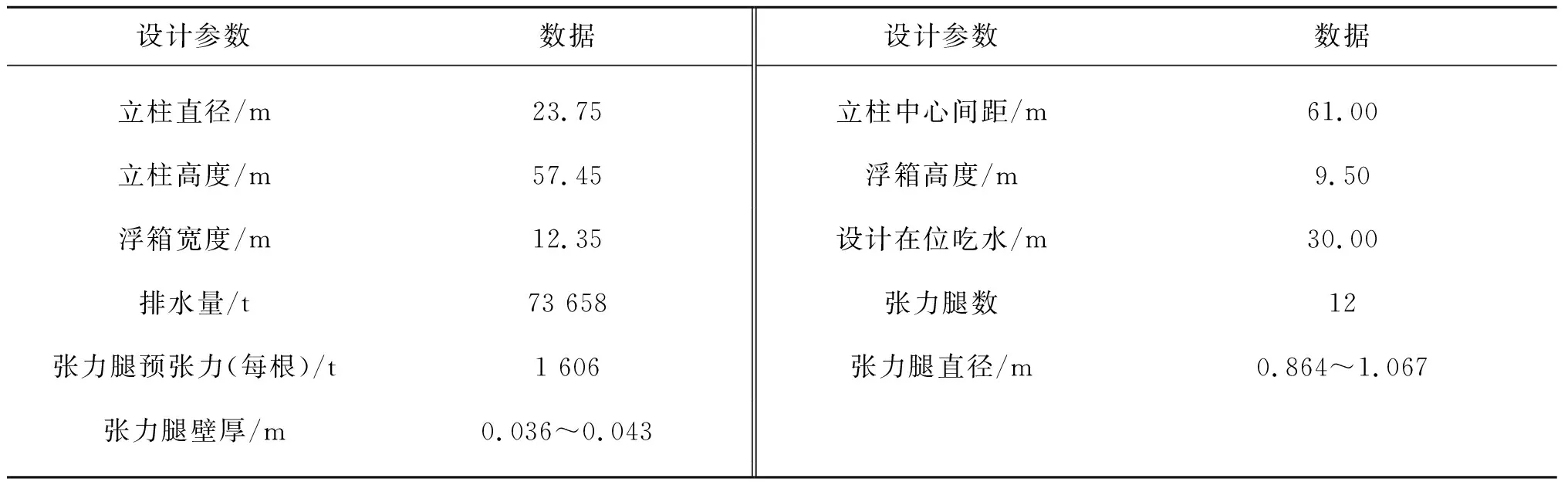
表3 TLP主尺度参数Tab. 3 Main dimension parameters of TLP

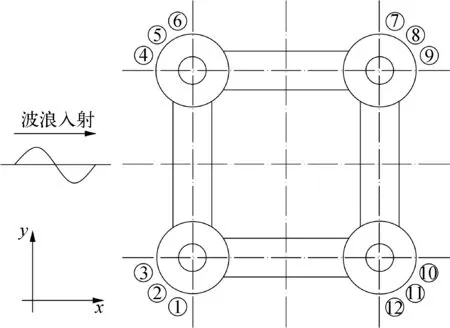
图8 张力腿布置Fig. 8 Distribution of tension leg

2.3.1 TLP长期响应预报

图9 DeepC结构模型和平台湿表面模型Fig. 9 Structure model in DeepC and wet surface model of platform

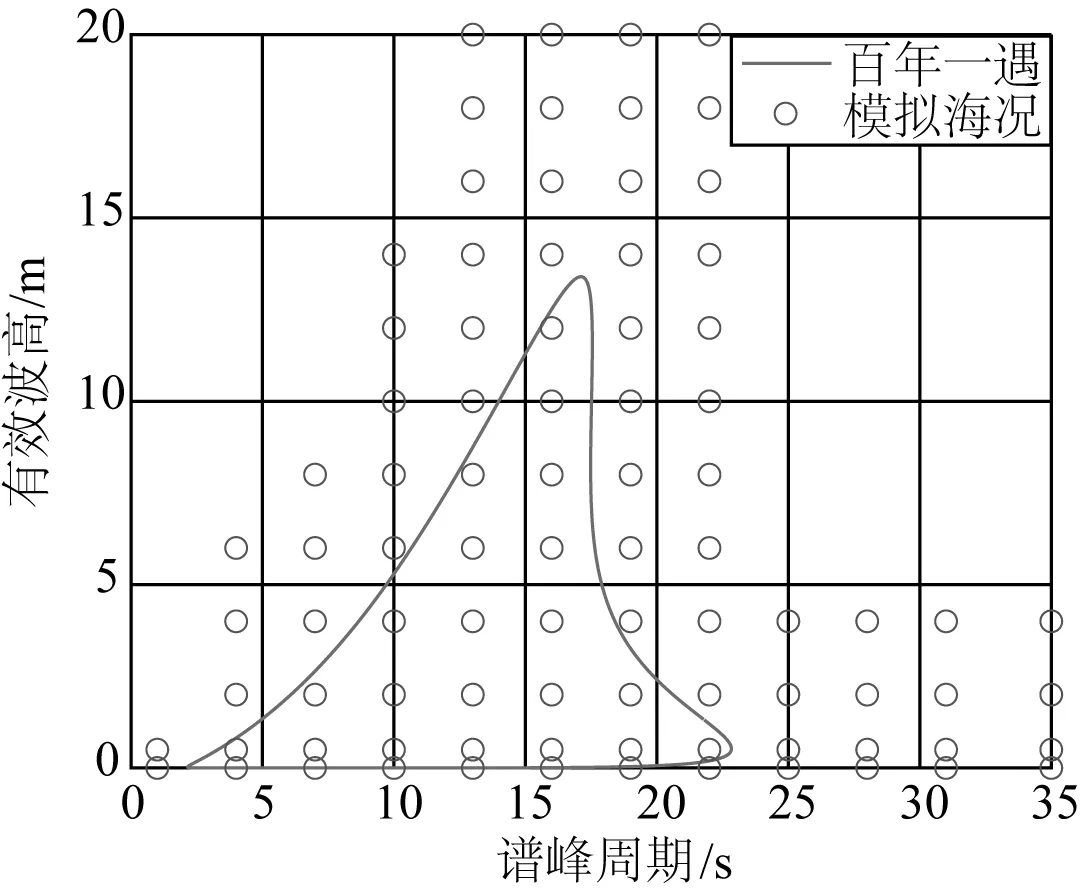
图10 用于模拟长期响应分析的海况Fig. 10 Sea states for simulating long-term response analysis

2.3.2 环境包络线法确定设计荷载的分位数

沿百年一遇包络线选择海况进行3 h短期响应分析，波浪谱峰周期范围约3～22 s，步长取1 s，在有效波高最大值附近加密取点，共选取28组海况(如图11所示)，其波浪参数见表4，波浪入射方向如图8所示。

图11 沿包络线选取关键海况Fig. 11 Retrieve design sea state along the contour lines

平台在每组海况条件下分别进行32次时域模拟，以每次模拟时最大张力为样本，用广义极值分布拟合各海况下结构短期张力极值分布FX3 h|HsTp(x|h,t)。图12为有效波高峰值附近海况S17～S22的拟合结果。将百年一遇的长期张力极值预报结果x100year=23 051 kN代入各海况的短期张力极值分布函数，得到各海况的短期分布对应长期预报结果的分位数α=FX3 h|HsTp(x100year|h,t)，计算结果见表4。

图12 广义极值分布拟合S17～S22海况下结构短期张力极值分布Fig. 12 The generalized extreme value distribution used to fit the short-term tension extreme value distribution of structures under S17～S22 sea state

采用环境包络线法预报结构百年一遇张力极值，应选取包络线上的海况中分位数最小值作为应用包络线法的分位数，以避免过高估计结构的百年一遇张力极值。如表4所示，工况S20的分位数取得最小值α=0.888。为保障结构安全，对于预报南海海域的张力腿平台在横浪作用下百年一遇的系泊张力而言，环境包络线法的分位数保守地取为α100year=0.9。

表4列出了各海况分位数α=0.9时对应的短期张力极值，工况S16～S24的谱峰周期为16.5～17.5 s，其0.9分位数对应的短期极值与长期预报结果x100year的误差均在3%以内，故可认为应用环境包络线法预报的长期极值具有一定稳定性，不会因海况选取小范围的差别而产生较大波动。

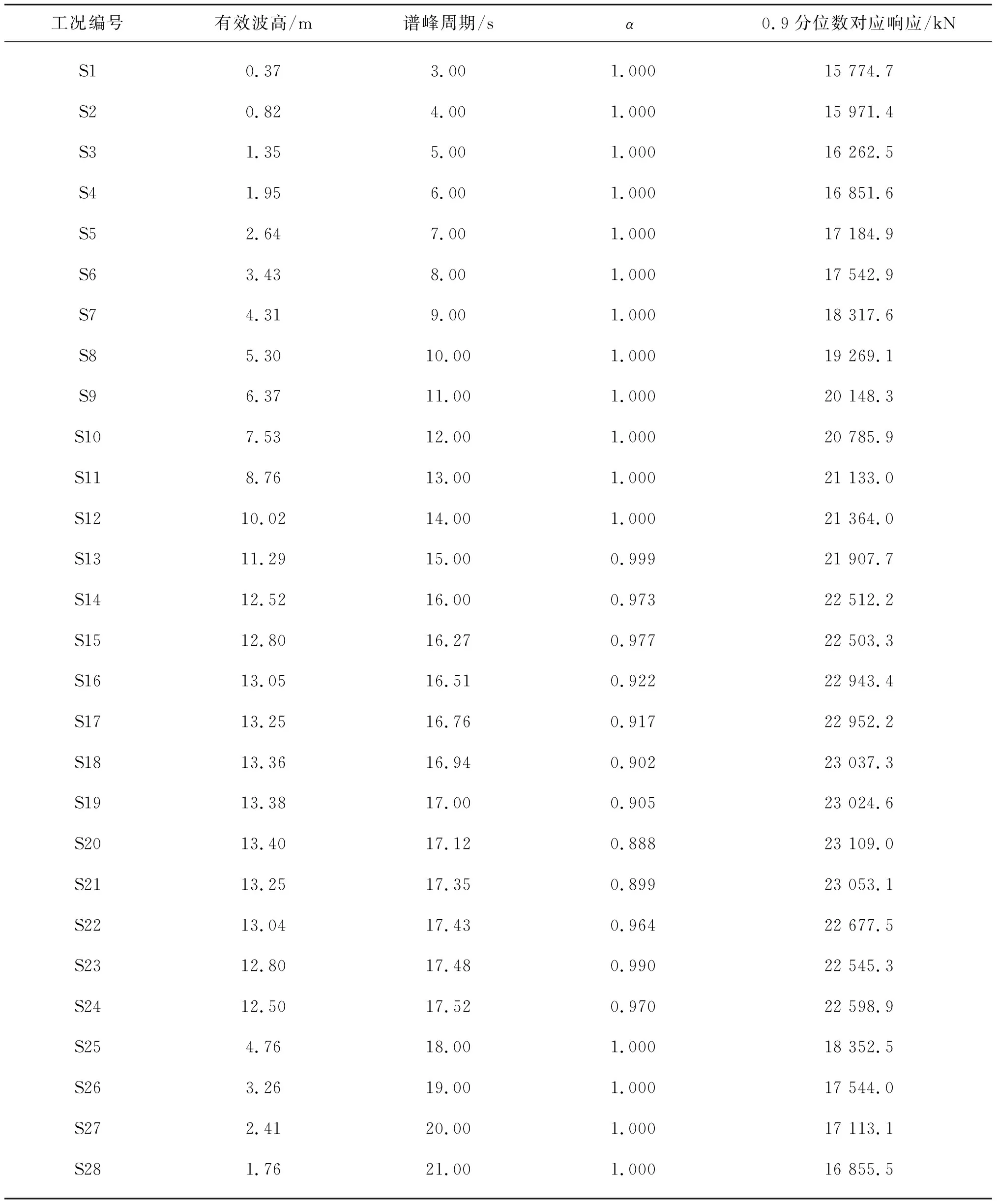
表4 海况波浪参数、长期预报对应的分位数及0.9分位数对应响应Tab. 4 Wave parameters of sea state,α and response corresponding to 0.9 quantiles

南海荔湾海域TLP在横浪作用下应用环境包络线法预报百年一遇张力极值的步骤如下：

1) 沿百年一遇环境包络线选取一组海况，谱峰周期步长可取为1.0～2.0 s；

2) 对各海况进行足够次数的时域模拟或模型测试，建立各海况下结构的3 h短期张力极值的累计概率分布。在张力极值较大的海况附近沿包络线加密取点作为补充海况，并计算其3 h短期张力极值的累计概率分布；

3 结 语

介绍了逆一阶可靠性方法(IFORM)在海洋结构物长期预报中的应用，简述了环境包络线法的应用方法。基于中国南海荔湾海域的环境资料，对该海域的有效波高及谱峰周期进行了统计分析，发现荔湾海域谱峰周期在有效波高条件下服从广义极值分布，而常用于描述波浪分布的Weibull-Lognorm条件分布模型并不适用于描述该海域的波浪分布特征，故建立了有效波高和谱峰周期的Weibull-Gev条件分布模型用于描述荔湾海域的波浪长期分布。

此外，基于IFORM绘制了荔湾海域的Hs-Tp概率包络线图，并结合中国南海TLP结构的长期分析结果，指出荔湾海域TLP在横浪作用下，系泊张力应用环境包络线法预报百年一遇极值对应分位数为0.9，为该海域TLP设计中横浪作用下系泊张力的长期极值预报提供快速有效的近似估计。

基于环境包络线的深水浮式平台极值响应长期预报方法，可广泛应用于深水浮式结构物在复杂海洋环境条件下的响应极值预报。进一步的，在获取目标海域风、浪、流联合概率密度特征后，结合对目标海洋平台的动力特征研究，可将方法应用在基于可靠性理论的风、浪、流联合作用的极值预报中。