基于FPGA的二维谱峰搜索算法硬件架构设计

房海松，司伟建

（哈尔滨工程大学，信息与通信工程学院，黑龙江 哈尔滨 150001）

0 引 言

经典的MUSIC算法是阵列测向技术中所用到的DOA估计方法之一，是空间谱估计测向理论的重要基石［1－2］。当前 大 多采 用 数字 信 号 处 理 （digital signal processing，DSP）芯片来实现二维或更高维的MUSIC算法，而同DSP相比，FPGA具有内部并行运行、可根据具体要求进行设计、运行速度更快等优点［3－4］。当前FPGA主要用于实现一维MUSIC算法，相比而言，二维MUSIC算法更适合应用于实际环境的DOA估计，研究二维 MUSIC算法更具有实际意义［5－6］。

谱峰搜索的FPGA实现的主要难点是计算量比较大，消耗的硬件资源比较多，因此在减少资源消耗的同时满足估计精度和实时性要求成为相关研究的热点［7］。在信号处理技术的发展过程中，谱峰搜索的FPGA实现的最初应用是针对一维信号进行处理［8－9］。针对不同的成本和速度要求，文献［10］采用一维脉动结构实现空间谱的计算，加速了谱峰搜索，在200 MHz工作频率下耗时57μs实现了精度为0．5°的一维搜索。文献［11］提出了基于Chirp－z变换的搜索方法，适合对一定区域进行精细的搜索，能有效提高搜索效率。文献［12］给出了适用于均匀线阵的实数化预处理方法和实用的空间谱定义，提高了算法的实时性，但是谱峰搜索的范围小，精度有限。

二维谱峰搜索包含更多的有用信息，更具有实用性。文献［13］在进行二维谱峰搜索的粗搜索时使用了二维数据插值，能有效地减少运算量。文献［14］在二维谱峰搜索中使用鸡群算法进行优化，寻优能力强，能快速搜索到谱峰。文献［15］设计了一种新的方案，能够减少执行时间和节省FPGA内部资源，完成二维谱峰搜索需要的时钟周期为31 500，方位角和仰角偏差均小于0．1°，估计精度高，满足实时性要求。文献［16］采用分步搜索法实现谱峰搜索，设计专用硬件电路实时计算方向向量以节省存储资源，具有精度高、速度快、资源消耗少的优势，在100 MHz工作频率的FPGA芯片上，实现估计精度为0．1°的二维谱峰搜索耗时2．989 ms。文献［17］通过空域划分实现了二维谱峰的并行搜索，有效地提高了搜索效率，并且能估计空域交界处的目标，但在计算谱值时使用等效值代替平方和，降低了估计精度。

本文针对实时性要求更高的二维MUSIC算法的谱峰搜索部分，合理设计出各个步骤的实现结构来解决实现时间与硬件资源消耗的平衡问题。二维谱峰搜索涉及的计算量较大，硬件资源消耗也较大，因此在保证资源消耗和估计精度满足要求的前提下，需使谱峰搜索的实现时间更少。本文所采用的硬件架构设计方法，方位角的搜索范围为0°～360°，仰角的搜索范围为30°～90°，当工作频率为100 MHz、估计精度为1°时，二维谱峰搜索实现时间仅需几微秒，具有很高的实时性。

1 谱峰搜索原理与实现步骤

本文采用8阵元均匀分布的平面圆阵，阵元分布如图1所示。

图1 阵元分布Fig．1 The distribution of array elements

采用分步搜索法来进行搜索，具体操作为：首先采用较大的步长（3°）在整个搜索范围进行粗搜索，确定谱峰的大致位置；然后在粗搜索的搜索结果附近采用较小的步长（1°）进行精搜索，得到准确的信号入射角（方位角θ和仰角φ）。这样可以在保证精度的前提下，大幅度降低计算量［18］。

谱峰搜索包括粗搜索的阵列流型矢量模块、谱值模块和谱峰粗搜索模块以及精搜索的阵列流型矢量模块、谱值模块和谱峰精搜索模块。谱峰搜索的流程框图如图2所示。

图2 谱峰搜索的流程框图Fig．2 The flowchart of spectrum peak search

其实现步骤如下：

1）第一步，选定一组方位角θ和仰角φ，根据8个阵元的坐标（x，y），可得到阵列流型矢量a（θ，φ）（1×8矩阵），如式（1）所示

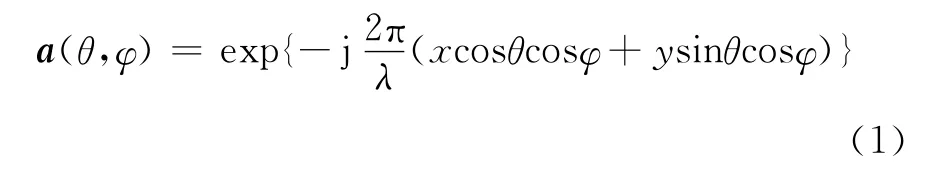
其中，λ为入射信号的波长。

2）第二步，将阵列流型矢量a（θ，φ）和噪声子空间UN（8×8矩阵，整体输入）按照式（2）进行内积累加运算，形成谱值。

3）第三步，对所有的谱值进行粗搜索。

4）第四步，对粗搜索选取的谱峰及其周围的谱值进行精搜索。精搜索同样需要经过第一步和第二步，然后再对谱值进行精搜索。

2 谱峰搜索模块分析

2．1 粗搜索

2．1．1 阵列流型矢量模块

此模块的目的是计算式（1），选定一组方位角和仰角，得到8×1矩阵，分别对应8个阵元。记新矩阵X，使其满足式（3）；并令新矩阵Y满足式（4），可得

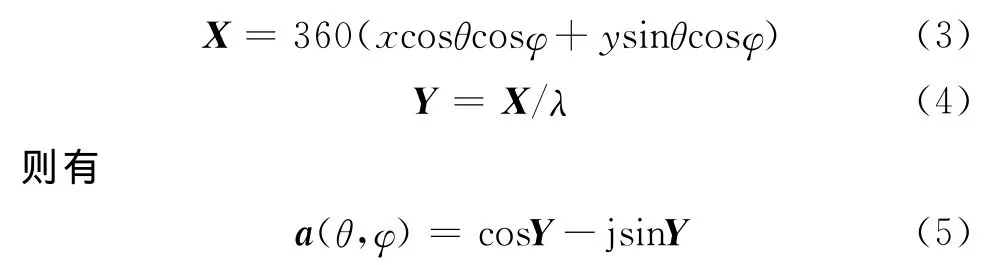
为了减小计算量，需要进行预处理，完成复数域到实数域的转换，且不改变最终结果［20－21］。因此，对于第1、2、3、4阵元，有

根据仰角取值30°、33°、…、87°、89°，可将阵列流型矢量模块分成21个小模块，对每个小模块制定查找表数据X。在每个小模块中，根据方位角取值0°、3°、…、357°将每个小模块分成120部分，每一部分均实施如图3所示的5个步骤。按照流水线结构实现这120部分，5个步骤根据时钟依次完成，从而有效提高了资源利用率，降低了资源消耗。

求取X时共制定21个并行的查找表，分别对应仰角30°、33°、…、87°、89°；每个查找表都有120个地址，分别对应方位角0°、3°、…、357°。值得注意的是，21个查找表并行消耗的是硬件资源，依次读取120个地址中的数据消耗的是时钟，这是经过权衡时钟消耗和硬件资源消耗得出的结果。求取正弦值和余弦值时为了减少查找表的资源消耗，需将第1、2、3、4阵元对应的余弦值转化为正弦值，并且将其他象限的正弦值均转化为第一象限的正弦值。由此可使该查找表的资源消耗降低到原来的八分之一，且不会增加误差。因此，制定84个并行的查找表即可。

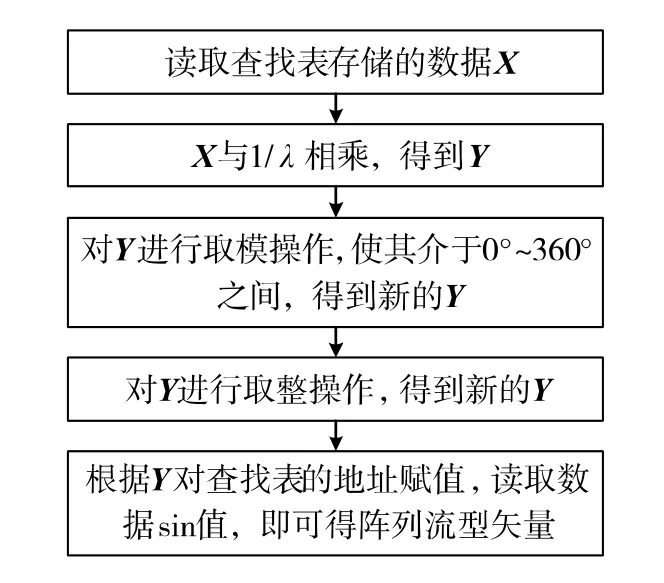
图3 阵列流型矢量模块实现步骤Fig．3 The realization steps of array flow pattern vector module

2．1．2 谱值模块

谱值模块本质是矩阵计算，在计算式（2）时，可先计算式（8），再计算式（9），得到谱值。其中新矩阵b为1×8矩阵。

同阵列流型矢量模块类似，谱值模块可分成22个小模块（仰角90°占用一个小模块），每个小模块同样采用流水线结构来实现谱值的计算。

现以仰角30°为示例说明对应谱值的计算过程。对于方位角0°、3°、…、357°来说，矩阵相乘中的运算均可分成4个步骤，如图4所示。步骤1、2与步骤3、4分别按照两条独自进行的流水线结构实现，如表1所示，采用流水线结构极大地减少了乘法器资源的消耗。仰角30°、33°、…、89°、90°（共22个）对应的谱值计算需并行进行。

图4 矩阵相乘的运算步骤Fig．4 The operational steps of matrix multiplication

表1 矩阵相乘的运算步骤的流水线结构Tab．1 The pipelined structure of the operational steps of matrix multiplication

2．1．3 谱峰粗搜索模块

由于仰角对应的谱值计算是并行进行的，所以每个时钟周期可得到22个并行的谱值。随着时钟周期的增加，依次可得到方位角0°、3°、…、357°（共120个）对应的谱值，共计2 640（22×120）个谱值。这些谱值按照图5的方式进行排列。分别以这些谱值为中心，与其周围的8个谱值相比较，判断这些中心谱值是否为极小值并记录下来。由于同一时钟两个相邻的仰角对应的谱值不可能同时为极小值，因此可将这些谱值分成11组，如表2所示。这样一来，谱峰粗搜索模块就可分为11个小模块。

将这11组得到的极小值（记为伪谱峰）分别按照从小到大的顺序排列，并分别选取前4个伪谱峰，共计得到44个伪谱峰。另外，由于仰角90°对应的谱值均相同，只需选取1个即可，因此谱峰粗搜索模块得到45个伪谱峰，然后根据这些伪谱峰进行精搜索。

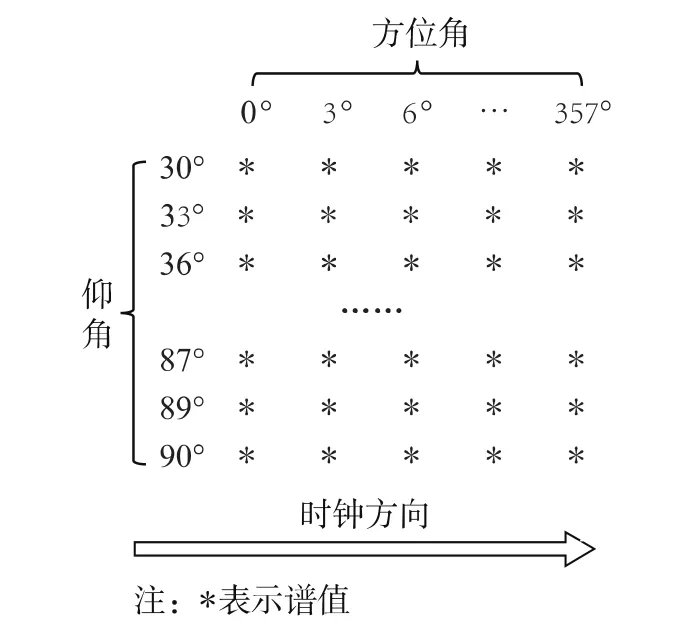
图5 谱值的排列方式Fig．5 The arrangement of spectral values

表2 谱峰粗搜索中谱值的分组情况Tab．2 The grouping of spectral values in spectrum peak coarse search

而在边缘搜索中，对于仰角30°，可与中心谱值相比较的谱值只有5个；对于仰角90°，在同一方位角的条件下，对应的谱值与仰角89°对应的谱值相比较。

2．2 精搜索

精搜索以1°为搜索步长，以粗搜索得到的44个伪谱峰（记为中心谱值，仰角90°对应的伪谱峰暂不考虑）为中心，重新计算其周围3×3区域的谱值（记为区域谱值）。每个区域有9个谱值，找到其中的最小值，共计44个，再将这44个最小值和仰角90°对应的伪谱峰按照从小到大的顺序排列，并选取前6个，即为最终谱峰。

为了保持时钟消耗和资源消耗的平衡，需合理分配这44个伪谱峰的先后次序。将粗搜索得到的第1、2组伪谱峰随时钟以串行的方式先后进行精搜索，同理，其他伪谱峰的分组情况如表3所示。因此需要对这6组伪谱峰进行并行操作，精搜索的执行过程如图6所示。

表3 伪谱峰的分组情况Tab．3 The grouping of pseudo spectrum peaks

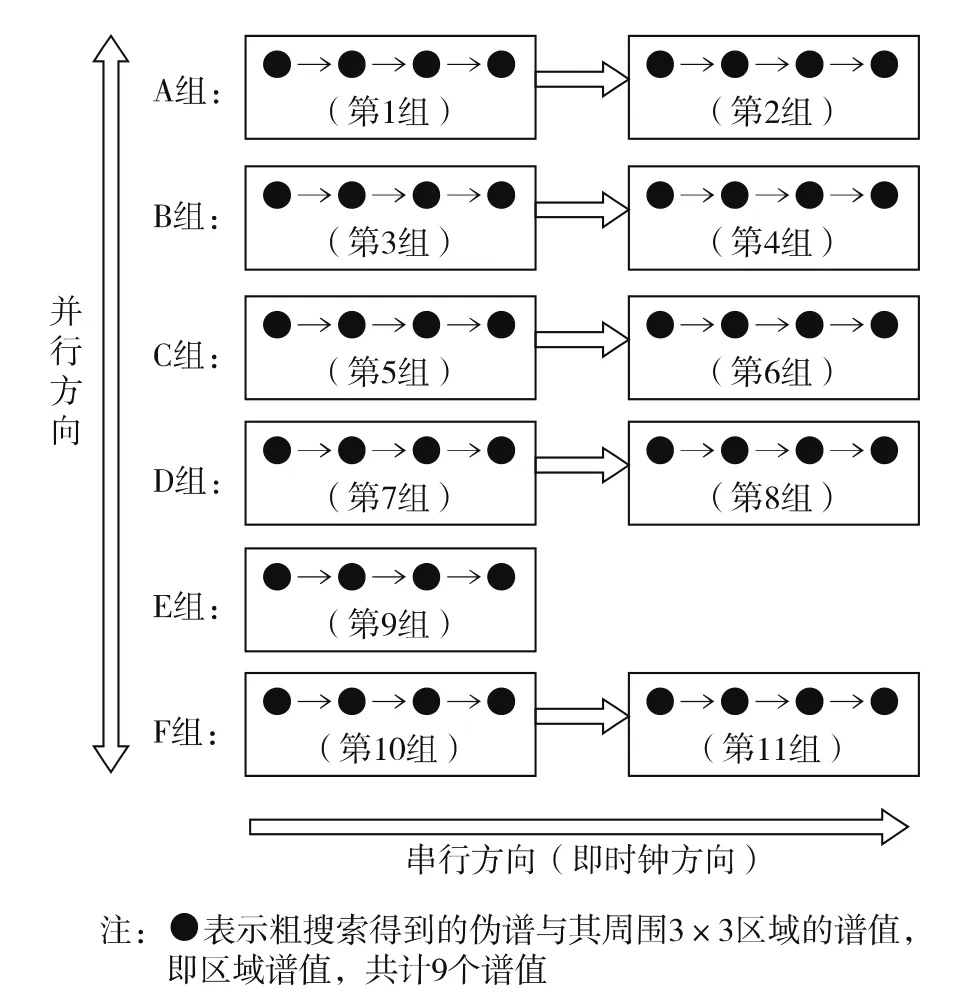
图6 精搜索的执行过程Fig．6 The execution of fine search

2．2．1 阵列流型矢量模块

根据粗搜索得到的6组伪谱峰，可将阵列流型矢量模块分成6个小模块，每个小模块和粗搜索的阵列流型矢量模块类似，也分为5个步骤，不同的是前者需根据粗搜索得到的伪谱峰对应的方位角和仰角确定谱值区域（3×3区域）。确定谱值区域需结合求取X的查找表实现，根据中心谱值的仰角与方位角可确定区域谱值的仰角与方位角，从而确定区域谱值对应的查找表及其地址。精搜索和粗搜索在阵列流型矢量模块求取sin值时复用同样的查找表，节省了大量的查找表资源。

2．2．2 谱值模块

本模块可分为6个小模块，和阵列流型矢量的6个小模块相对应，分别对应A、B、C、D、E、F组伪谱峰，且并行计算谱值。和粗搜索的谱值模块相同，精搜索的谱值模块采用相同的流水线结构来实现谱值的计算。

2．2．3 谱峰精搜索模块

谱峰精搜索模块只有一个模块。以A组的第一个伪谱峰为例，其对应的区域谱值有9个，在这9个谱值中找到最小值。同理，分别在B、C、D、E、F组的第一个伪谱峰对应的区域谱值中找到最小值。然后将这6个最小值按照从小到大的顺序排列。随着时钟的进行，分别在A、B、C、D、E、F组的第二个伪谱峰对应的区域谱值中找到最小值，并将这些最小值和之前得到的6个最小值按照从小到大的顺序排列。如此，直到把所有伪谱峰对应的区域谱值的最小值进行排序。最后，将粗搜索得到的仰角90°对应的伪谱值与这些最小值进行排序，得到排序后的6个谱值，即为最终结果。

3 仿真验证与性能分析

3．1 FPGA实现

为了对本文提出的二维谱峰搜索设计方案进行性能测试，首先采用Verilog语言，在Vivado工具中进行综合仿真，然后将设计下载到Xilinx公司Virtex－7系列FPGA的XC7V690T开发板中进行实际验证。完成所有模块需要377个时钟周期，估计精度为1°，当工作频率为100 MHz时，实现时间为3．77μs。硬件资源消耗如表4所示。

表4 二维谱峰搜索硬件资源消耗Tab．4 The hardware resource consumption of two－dimensional spectrum peak search

3．2 仿真验证

采用8阵元均匀圆阵的阵元模型，入射信号的频率为3 GHz，采样快拍数为128，要求估计精度为1°且实现时间为5μs以内。信噪比分别为4～15 dB，在100 MHz工作频率的FPGA芯片上完成了12组数据仿真实验，每个信噪比下分别进行了500次实验，得到方位角和仰角，在单信号源和双信号源条件下其均方根误差分别如图7和图8所示。可以看出，单信号源和双信号源对应的方位角和仰角均满足1°的精度要求。随着信噪比的增加，误差越来越小。

图7 单信号源的仿真结果Fig．7 The simulation results of single signal source

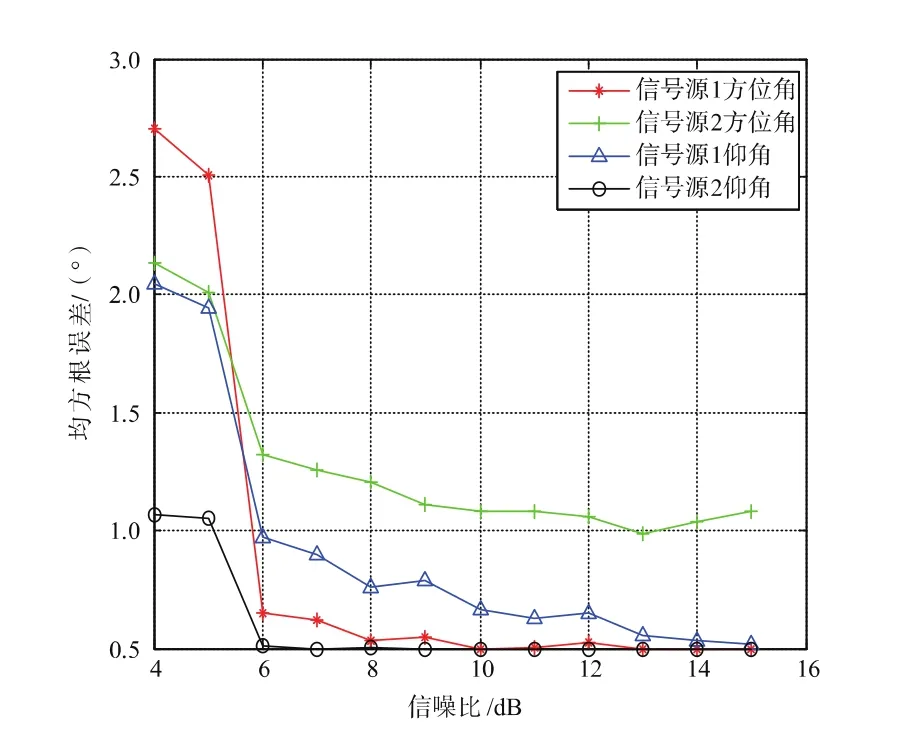
图8 双信号源的仿真结果Fig．8 The simulation results of dual signal source

3．3 性能分析

对于二维谱峰搜索，实现时间是衡量其性能的重要依据。本文与其他二维谱峰搜索的实现方案性能对比如表5所示。从表5中可以看出，本文谱峰搜索的速度明显高于其他文献给出方案的搜索速度，实时性更高。本文方案与文献［15］、文献［16］的方案都采用分步搜索法进行搜索，都采用查找表计算阵列流型矢量。但是同本文方案相比，文献［15］、文献［16］的方案流水化程度较低，导致硬件资源的消耗和算法的实现时间大幅度增加。而且，本文方案优于其他文献方案之处还在于增加信号源不会增加谱峰搜索的实现时间。

表5 二维谱峰搜索方案性能对比Tab．5 The performance comparison of two－dimensional spectrum peak search

4 结束语

本文针对二维谱峰搜索的实时性进行了深入研究，提出了一种基于FPGA的二维谱峰搜索实现方案。该方案采用分步搜索法实现谱峰搜索，合理设计了谱峰搜索各个步骤的实现结构，大幅度减少了计算量和计算复杂度，从而在满足估计精度的同时解决了实现时间与硬件资源消耗的平衡问题。阵列流型矢量计算、谱值计算和谱峰粗（精）搜索3个模块完全流水化，模块交叉重叠进行，用硬件资源交换实现时间，并且通过模块复用降低资源消耗，从而大大提高了计算效率，极大地缩短了整体时间。与现有其他方案相比，该二维谱峰搜索实现结构的主要优点在于速度快，实时性高，具有较高的工程应用价值。